These Solutions are part of NCERT Solutions for Class 11 Physics. Here we have given NCERT Solutions for Class 11 Physics Chapter 7 System of Particles and Rotational Motion
Class 11 Physics Chapter 7 System of Particles and Rotational Motion NCERT Solutions
System of Particles and Rotational Motion NCERT Solutions
Question 1.
Give the location of the center of mass of a (i) sphere, (ii) cylinder, (iii) ring, and (iv) cube, each of uniform mass density. Does not the center of mass of a body necessarily lie inside the body?
Answer:
The Centre of the mass of sphere cylinder, ring, and cube with homogenous mass distribution lies at its geometric centre. It is not necessary that CM (centre of mass) lies inside the body as in the cases of the ring or hollow hemisphere.
Question 2.
In the HCl molecule, the separation between the nuclei of the two atoms is about 1.27 A (1 A = 10-10 m). Find the approximate location of the CM of the molecule, given that a chlorine atom is about 35.5 times as massive as a hydrogen atom and nearly all the mass of an atom is concentrated in its nucleus.
Answer:
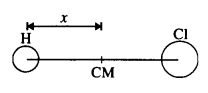
Let us choose the nucleus of the hydrogen atom as the origin for measuring distance.
Mass of hydrogen atom, m1 = 1 unit (say)
Mass of chlorine atom, m2 = 35.5 units (say)
Now, x1= 0 and x2 = 1.27 A = 1.27 x 10-10 m
The distance of C.M. of HCl molecule from the origin is given by
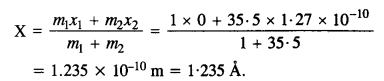
Question 3.
A child sits stationary at one end of a long trolley moving uniformly with a speed V on a smooth horizontal floor. If the child gets up and runs about on the trolley in any manner, what is the speed of C.M. of the (trolley + child) system?
Answer:
There is no external force acting on the child and the trolley system, hence the momentum of the entire system is conserved. Therefore the CM keeps moving with its initial speed of V in the same direction.
Question 4.
Show that the area of the triangle contained between the vectors a and b is one-half of the magnitude of a x b.
Answer:
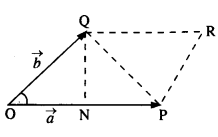

Question 5.
Show that a.(b x c) is equal in magnitude to the volume of the parallelepiped formed on the three vectors a, b and c.
Answer:
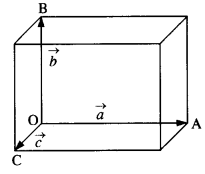
Let a parallelepiped be formed on the three vectors
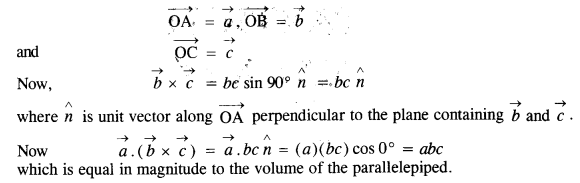
Question 6.
Find the components along the x, y, z axes of the angular momentum \(\vec { l } \)of a particle, whose position vector is \(\vec { r } \) with components x, y, z and momentum is with components x, y, z and momentum is \(\vec { p } \) with components px, py and pz. Show that if the particle moves only in the x-y plane, the angular momentum has only a z-component.
Answer:
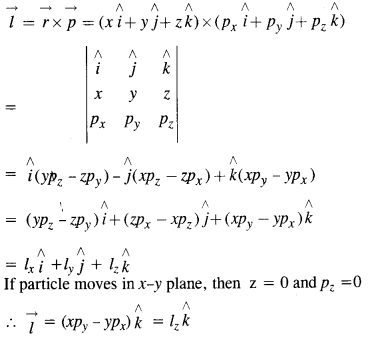
Question 7.
Two particles, each of mass m and speed u, travel in opposite directions along parallel lines separated by a distance d. Show that the vector angular momentum of the two-particle system is the same whatever be the point about which the angular momentum is taken.
Answer:

Question 8.
A non-uniform bar of weight W is suspended at rest, by two strings of negligible weight as shown in Fig. The angles made by the strings with the vertical are 36.9° and 53.1° respectively. The bar is 2 m long. Calculate the distance d of the center of gravity of the bar from its left end.
Answer:
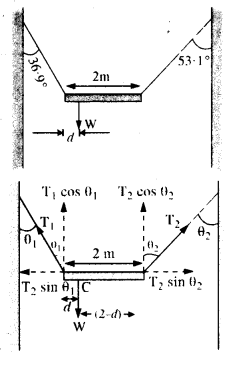
As is clear from Fig.,
θ1 = 36.9°,θ2 = 53.1°.
If T1, T2 are the tensions in the two strings, then for equilibrium along the horizontal,
T1 sin θ1 = T2 sin θ2

Question 9.
A car weighs 1800 kg. The distance between its front and back axles is 1.8 m. Its center of gravity is 1.05 m behind the front axle. Determine the force exerted by the level ground on each front wheel and each back wheel.
Answer:
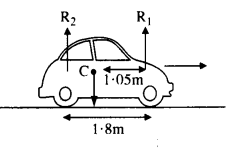
Here, m = 1800 kg
Distance of center of gravity (C) behind the front axle = 1.05 m.
Let R1. R2 be the force exerted by the level ground on front wheels and back wheels. As is clear from fig.,
R1+ R2 = mg = 1800 x 9.8 = 17640 N
For rotational equilibrium about C,
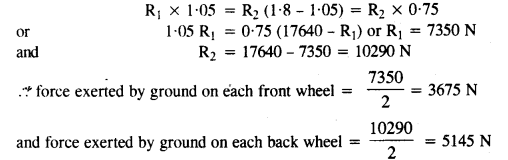
Question 10.
(a) Find the moment of inertia of a sphere about a tangent to the sphere, given the moment of inertia of the sphere about any of its diameters to be 2 MR2/5, where M is the mass of the sphere and R is the radius of the sphere.
(b) What is the moment of inertia of a uniform disc of radius R and mass M about an axis
(1) passing through its center and normal to the disc
(2) passing through a point on its edge and normal to the disc?
The moment of inertia of the disc about any of its diameters is given to be \(\frac { 1}{ 4 } \) MR2.
Answer:


Question 11.
Torques of equal magnitude are applied to a hollow cylinder and a solid sphere, both having the same mass and radius. The cylinder is free to rotate about its standard axis of symmetry, and the sphere is free to rotate about an axis passing through its center. Which of the two will acquire a greater angular speed after a given time?
Answer:
M.I. of the cylinder =I1= MR2
M.I. of the cylinder=I2=\(\frac {2}{ 5 } \) MR2

ω = ω0 +αt, therefore sphere acquires a greater speed than a cylinder as α2 >α1
Question 12.
A solid cylinder of mass 20 kg rotates about its axis with angular speed 100 rad s-1. The radius of the cylinder is 0.25 What is the kinetic energy associated with the rotation of the cylinder? What is the magnitude of angular momentum of the cylinder about its axis?
Answer:
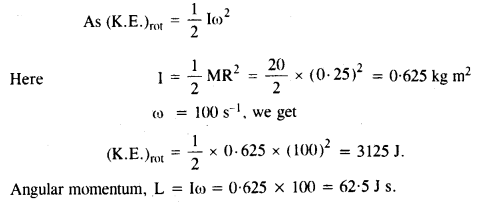
Question 13.
(a) A child stands at the center of a turntable with his two arms outstretched. The turntable is set to rotate with an angular speed of 40 rev/min. How much is the angular speed of the child if he folds his hands back and thereby reduces his moment of inertia to 2/5 times the initial value? Assume that the turntable rotates without friction.
(b) Show that the child’s new kinetic energy of rotation is more than the initial kinetic energy of rotation. How do you account for this increase in kinetic energy?
Answer:
(a) Suppose, the initial moment of inertia of the child is I1. Then the final moment of inertia,
I2 = \(\frac {2}{ 5 } \)
Also, v1= 40 rev min
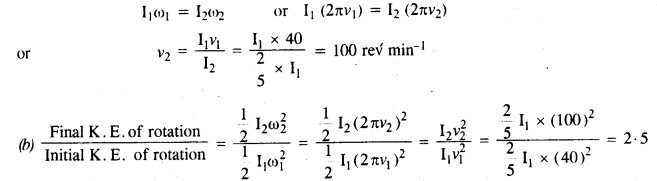
Clearly, final (K.E.)rot becomes more because the child uses his internal energy when he folds his hands to increase the kinetic energy.
Question 14.
A rope of negligible mass is wound round a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N? What is the linear acceleration of the rope? Assume that there is no slipping.
Answer:
Here, M = 3 kg, R = 40 cm = 0.4 m
M.I. of the hollow cylinder about its axis = I = MR2 = 3 x (0.4)2 = 0.48 kg m2
When the force of 30 N is applied over the rope wound on the cylinder, the torque will act on the cylinder. It is given by
τ= FR = 30 x 0.4 = 12 N m
If a is angular acceleration produced, then
τ = Iα
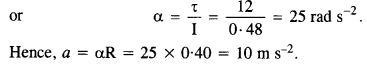
Question 15.
To maintain a rotor at a uniform angular speed of 200 rad s-1, an engine needs to transmit a torque of 180 Nm. What is the power required by the engine? (Note: uniform angular velocity in the absence of friction implies zero torque. In practice, applied torque is needed to counter frictional torque). Assume that the engine is 100% efficient.
Answer:
Here τ = 18 Nm, ω = 200 rad s-1
P =τω
∴ V P = 180 x 200 = 36000 W = 36 kW.
Question 16.
From a uniform disk of radius R, a circular section of radius R/2 is cut out. The center of the hole is at R/2 from the center of the original disc. Locate the center of mass of the resulting flat body.
Answer:
Let the mass of disc = M
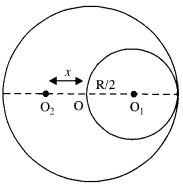
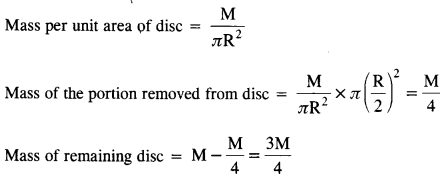
Mass of the portion removed from the disc is concentrated at [O] and the mass of the remaining disc is supposed to be concentrated at O2 at a distance x from the center of the disc (O).
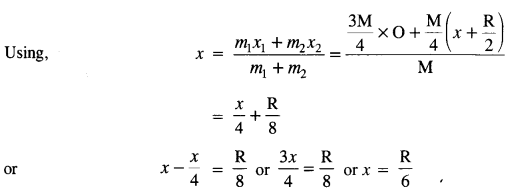
Question 17.
A meter stick is balanced on a knife-edge at its center. When two coins, each of mass 5 g are put one on top of the other at the 12*0 cm mark, the stick is found to be balanced at 45-0 cm. What is the mass of the meter stick?
Answer:
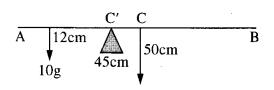
Let m be the mass of the stick concentrated at C, the 50 cm mark (Fig.)
According to the principle of moments
Moment of the mass of coins about C’ = moment of the mass of the rod about C’
10 g (45 – 12) = mg (50 – 45)
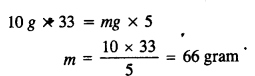
Question 18.
A solid sphere rolls down two different inclined planes of the same heights but different angles of inclination. Will it reach the bottom with the same speed in each case? Will it take longer to roll down one plane than the other? If so, which ones and why
Answer:
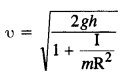
Since sphere rolls down two inclined planes of same height, so velocity of sphere in both the cases is same.
![]()
Since θ is different in both cases, so sphere will take longer time in case of inclined plane having a smaller inclination angle (0).
Question 19.
A hoop of radius 2 m weighs 100 kg. It rolls along a horizontal floor so that its center of mass has a speed of 20 cm/s. How much work has to be done to stop it?
Answer:
Here, R = 2m, 100 kg
u = 20 cm/s = 0.2 m/s
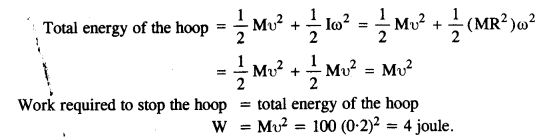
Question 20.
The oxygen molecule has a mass of 5.30 x 10–26 kg and a moment of inertia of 1.94 x 10-46 kg m2 about an axis through its center perpendicular to the line joining the two atoms. Suppose the mean speed of such a molecule in a gas is 500 m/s and that its kinetic energy of rotation is two-thirds of its kinetic energy of translation. Find the average angular velocity of the molecule.
Answer:
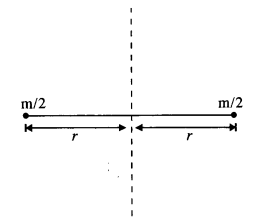
Here, m = 5.30 x 10–26 kg
I = 1.94 X 10-46 kg m2
υ = 500 m/s
If m/2 is mass of each atom of oxygen and 2r is distance between the two atoms as shown in Fig., then
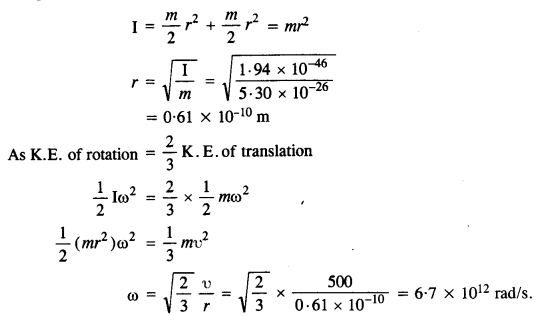
Question 21.
A cylinder rolls up an inclined plane of the angle of inclination of 30°. At the bottom of the inclined plane, the center of mass of the cylinder has a speed of 5 m/s.
(a) How far will the cylinder go up the plane?
(b) How long will it take to return to the bottom?
Answer:
Here, θ = 30°, υ= 5 m/s
Let the cylinder go up the plane upto a height h.
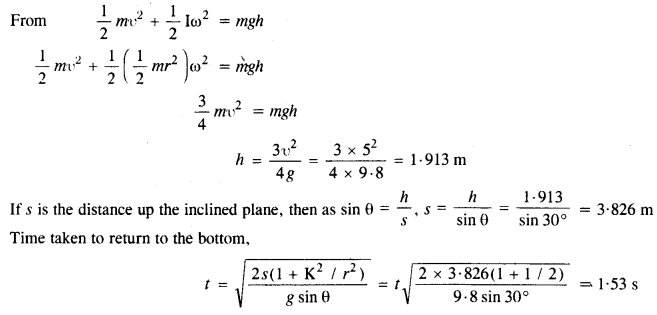
Question 22.
As shown in Fig., the two sides of a step ladder BA and CA are 1.6 m long and hinged at A. A rope DE, 0.5 m is tied halfway up. A weight of 40 kg is suspended from a point F, 1.2 m from B along with the ladder BA. Assuming the floor to be frictionless and neglecting the weight of the ladder, find the tension in the rope and forces exerted by the floor on the ladder. (Take g=9.8 m/s2)
(Hint. Consider the equilibrium of each side of the ladder separately.)
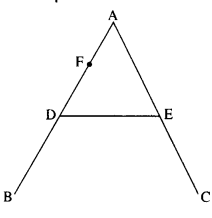
Answer:
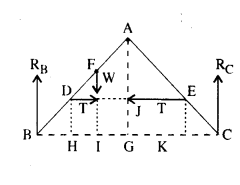
Let T be the tension in the rope DE. RB and Rc are the normal reactions of the floor at B and C respectively.
Since the ladder is in translational equilibrium, therefore, RB + Rc = W = mg = 40 x 9.8 = 392 N …(i)
A ladder is also in rotational equilibrium, therefore, net torque on arms AB and AC is zero.
For arm AB, RB x BG – W x IG = T x AJ
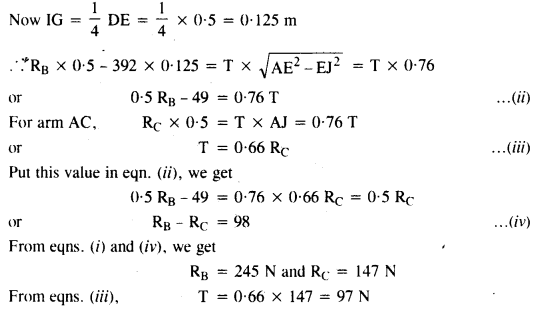
Question 23.
A man stands on a rotating platform, with his arms stretched horizontally holding a 5 kg weight in each hand. The angular speed of the platform is 30 revolutions per minute. The man then brings his arms close to his body with the distance of each weight from the axis changing from 90 cm to 20 cm. The moment of inertia of the man together with the platform may be taken to be constant and equal to 7.6 kg m2. What is his new angular speed? (Neglect friction.)Is kinetic energy conserved in the process? If not, from where does the change come about?
Answer:
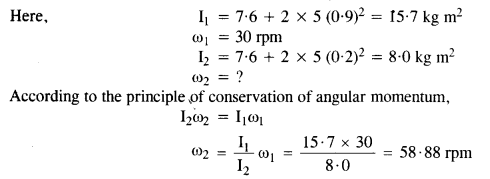
No, kinetic energy is not conserved in the process. In fact, as a moment of inertia decreases, the K.E. of rotation increases. This change comes about as work is done by the man in bringing his arms closer to his body.
Question 24.
A bullet of mass 10 g and speed 500 m/s is fired into a door and gets embedded exactly at the center of the door. The door is 1.0 m wide and weighs 12 kg. It is hinged at one end and rotates about a vertical axis practically without friction. Find the angular speed of the door just after the bullet embeds into it.(Hint. The moment of inertia of the door about the vertical axis at one end is ML2/3.)
Answer:
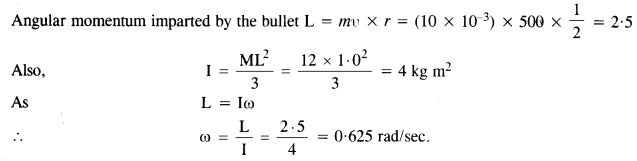
Question 25.
Two discs of moments of inertia I, and I2 about their respective axes (normal to the disc and passing through the center), and rotating with angular speeds ω1 and ω2 are brought into contact face to face with their axes of rotation coincident,
(a) What is the angular speed of the two-disc system?
(b) Show that the kinetic energy of the combined system is less than the sum of the initial kinetic energies of the two discs. How do you account for this loss in energy? Take ω1 ≠ω2
Answer:
Initial angular moment of the discs = I1ω1 + I2ω2
M.I. of two discs combined as a system = I1+ I2
Final angular moment of the combination = (I+ I2)ω
By using the law of conservation of angular momentum,
we get I1ω1 + I2ω2 = ( I1+ I2 )ω
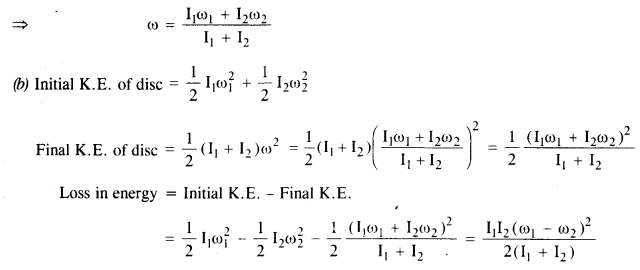
As the above term comes out to be positive, thus, the rotational kinetic energy of the combined disc is less than the total initial energy.
Question 26.
(a) Prove the theorem of perpendicular axes (Hint. Square of the distance of a point (x, y) in the x-y plane from an axis perpendicular to the plane through the origin is x2 + y2).
(b) Prove the theorem of parallel axes (Hint. If the center of mass is chosen to be the origin εmiri= 0).
Answer:
(a) The theorem of perpendicular axes: According to this theorem, the moment of inertia of a plane lamina (i.e., a two-dimensional body of any shape/size) about any axis OZ perpendicular to the plane of the lamina is equal to sum of the moments of inertia of the lamina about any two mutually perpendicular axes OX and OY in the plane of lamina, meeting at a point where the given axis OZ passes through the lamina. Suppose at the point ‘R’ m{ particle is situated moment of inertia about Z-axis of lamina
= moment of inertia of the body about r-axis
= moment of inertia of the body about the y-axis.
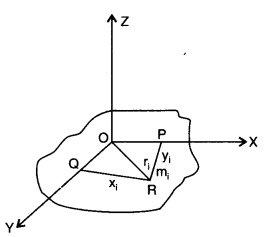
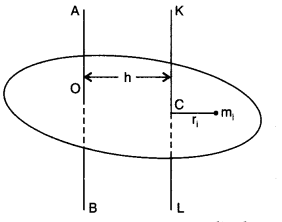
(b) Theorem of parallel axes: According to this theorem, a moment of inertia of a rigid body about any axis AB is equal to the moment of inertia of the body about another axis KL passing through centre of mass C of the body in a direction parallel to AB, plus the product of total mass M of the body and square of the perpendicular distance between the two parallel axes. If h is the perpendicular distance between the axes AB and KL, then Suppose the rigid body is made up of n particles m1, m2, …. mn, mn at perpendicular distances r1, r2, ri…. rn. respectively from the axis KL passing through centre of mass C of the body.
If h is the perpendicular distance of the particle of mass m{ from KL, then

Question 27.
Prove the result that the velocity of translation of a rolling body (like a ring, disc, cylinder, or sphere) at the bottom of an inclined plane of a height h is given by using dynamical consideration (i.e., by consideration of forces and torques). Note k is the radius of gyration of the body about its symmetry axis, and R is the radius of the body. The body starts from rest at the top of the plane.
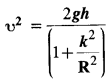
Answer:
When a body rolls down an incline of height h, we apply the principle of conservation of energy.
K.E. of translation + K.E. of rotation = P.E. at the top.
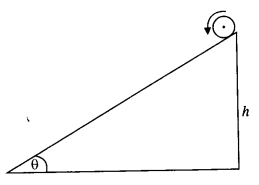
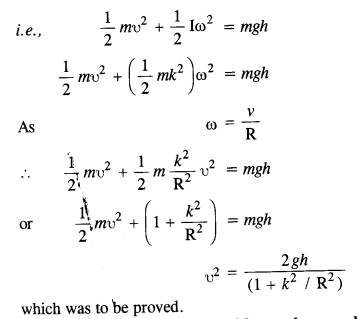
Question 28.
A disc rotating about its axis with angular speed ω0 is placed lightly (without any translational push) on a perfectly frictionless table. The radius of the disc is R. What are the linear velocities of the points A, B, and C on the disc shown in Fig.? Will the disc roll in the direction indicated?
Answer:
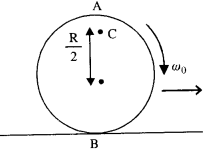

The disc will not roll in the given direction because friction is necessary for the same.
Question 29.
Explain why friction is necessary to make the disc in Fig. shown in Q. 28, roll in the direction indicated.
(a) Give the direction of frictional force at B, and the sense of frictional torque, before perfect rolling begins.
(b) What is the force of friction after perfect rolling begins?
Answer:
To make the disc roll, torque is required. This torque will be provided by the frictional force.
(a) At point B, the frictional force supports the angular motion of this point, so frictional force is in the direction of the arrow itself. The direction of frictional torque is normal to the paper in an outward direction.
(b) Frictional force tries to decrease the velocity of point B. When this velocity becomes zero, perfect rolling beings. For zero velocity, the force of friction also becomes zero.
Question 30.
A solid disc and a ring, both of radius 10 cm are placed on a horizontal table simultaneously, with an initial angular speed equal to 10 π rad s-2. Which of the two will start to roll earlier? The coefficient of kinetic friction is μk = 0.2.
Answer:
Force of friction (μk mg) produces an acceleration a in the center of mass (moving with υ = R ω)
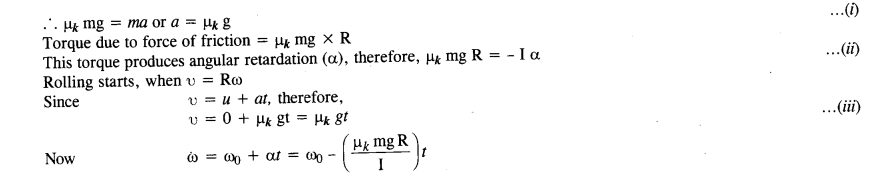
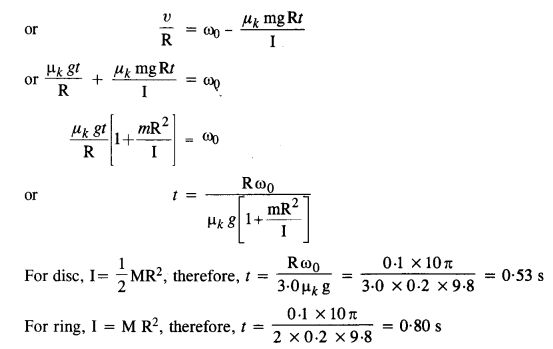
Question 31.
A cylinder of mass 10 kg and radius 15 cm is rolling perfectly on a plane of inclination 30°. The coefficient of the static friction μs = 0.25.
(a) How much is the force of friction acting on the cylinder?
(b) What is the work done against friction during rolling?
(c) If the inclination 6 of the plane is increased, at what value of 6 does the cylinder begin to skid, and not roll perfectly?
Answer:
Here M = 10 kg; R = 15 cm = 0.15 m; μs= 0.25; θ = 30°
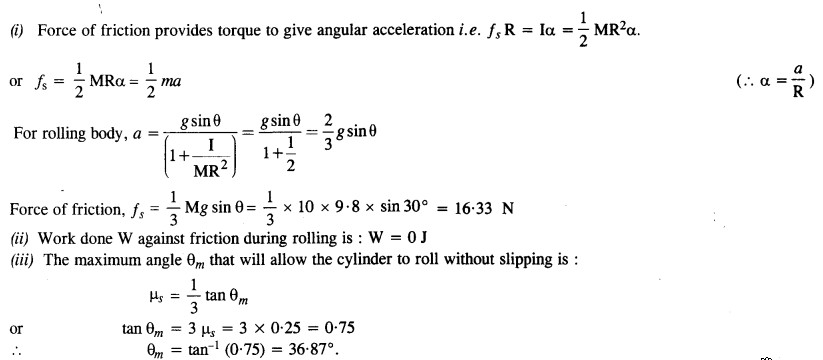
Question 32.
Read each statement below carefully, and state, with reason, it is true or false:
(a) During rolling, the force of friction acts in the same direction as the direction of motion of the CM of the body.
(b) The instantaneous speed of the point of contact during rolling is zero.
(c) The instantaneous acceleration of the point of contact during rolling is zero.
(d) For perfect rolling motion, work done against friction is zero.
(e) A wheel moving down a perfectly frictionless inclined plane will undergo a slipping (not rolling) motion.
Answer:
(a) True (The force of friction helps in rolling a body).
(b) True (A rolling body is considered as a rotating body about an axis passing through the point of contact).
(c) False (Since the body is rotating, so its instantaneous acceleration cannot be zero).
(d) True (Since the point of contact is at rest, so work done is zero).
(e) True (In the case of the frictionless inclined plane, there is no tangential force of friction (or torque) and hence wheel cannot roll).
We hope the NCERT Solutions for Class 11 Physics Chapter 7 System of Particles and Rotational Motion, help you. If you have any query regarding NCERT Solutions for Class 11 Physics Chapter 7 System of Particles and Rotational Motion, drop a comment below and we will get back to you at the earliest.
Class 11 Physics NCERT Solutions
- Physical World Class 11 NCERT Solutions
- Units and Measurements Class 11 NCERT Solutions
- Motion in a Straight Line Class 11 NCERT Solutions
- Motion in a Plane Class 11 NCERT Solutions
- Laws of Motion Class 11 NCERT Solutions
- Work Energy and Power Class 11 NCERT Solutions
- System of Particles and Rotational Motion Class 11 NCERT Solutions
- Gravitation Class 11 NCERT Solutions
- Mechanical Properties of Solids Class 11 NCERT Solutions
- Mechanical Properties of Fluids Class 11 NCERT Solutions
- Thermal Properties of Matter Class 11 NCERT Solutions
- Thermodynamics Class 11 NCERT Solutions
- Kinetic Theory Class 11 NCERT Solutions
- Oscillations Class 11 NCERT Solutions
- Waves Class 11 NCERT Solutions