These Solutions are part of NCERT Solutions for Class 11 Chemistry. Here we have given NCERT Solutions for Class 11 Chemistry Chapter 5 States of Matter Solids, Liquids and Gases.
Class 11 Chemistry Chapter 5 States of Matter Solids, Liquids and Gases NCERT Solutions
States of Matter Solids, Liquids and Gases NCERT Solutions
Question 1.
What will be the minimum pressure required to compress 500 dm3 of air at 1 bar to 200 dm3 at 30° C ?
Answer:
From the given data :
P1 = 1 bar P2 = ?
V1 = 500 dm3 V2 = 200 dm3
P1V1 = V1P2 or P2 = \(\frac { { P }_{ 1 }{ V }_{ 1 } }{ { V }_{ 2 } } \)
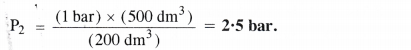
Question 2.
A vessel of 120 mL capacity contains a certain amount of gas at 35°C and 1.2 bar pressure. The gas is transferred to another vessel of volume 180 mL at 35°C. What would be its pressure ?
Answer:
From the given data :
P1 = 1.2 bar P2 = ?
V1 = 120 mL V2 = 180 mL
Since temperature is constant, Boyle’s Law can be applied.
P1V1 = V1P2 or P2 = \(\frac { { P }_{ 1 }{ V }_{ 1 } }{ { V }_{ 2 } } \) ; P2 = \(\frac { (1.2bar)\times (120mL) }{ 180mL } \) = 0.8 bar
Question 3.
Using the equation of state PV = nRT show that at a given temperature, the density of the gas is proportional to the gas pressure p.
Answer:

Question 4.
At 0°C, the density of a gaseous oxide at 2 bar is the same as that of nitrogen at 5 bar. What is the molecular mass of the oxide ?
Answer:

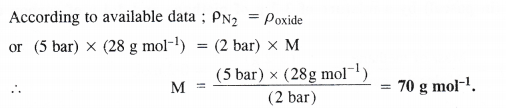
Question 5.
Pressure of lg of an ideal gas A at 27°C is found to be 2 bar. When 2g of another ideal gas B is introduced in the same flask at same temperature, the pressure becomes 3 bar. Find the relationship between their molecular masses.
Answer:
Let MA and MB be the molar masses of the two gases A and B. According to available data :

Question 6.
The drain cleaner, ‘Drainex’ contains small bits of aluminium which react with caustic soda to produce hydrogen. What volume of hydrogen at 20°C and one bar will be released when 0.15 g of aluminium reacts ?
Answer:
Step I. Calculation of the volume of hydrogen released under N. T.P. conditions.
The chemical equation for the reaction is :
2Al + 2NaOH + 2H2O → 2NaAl02 + 3H2
2×27=54 g Sod. meta aluminate 3×22400 mL
54g of Al at N.T.P. release H2 gas = 3 × 22400 mL
0.15g of Al at N.T.P. release H2 gas = \(\frac { (3\times 22400mL)\quad \times \quad (0.15g) }{ (54g) } \) =186.7mL.
Step II. Calculation of volume of hydrogen released at 20°C and 1 bar pressure.

Question 7.
What will be the pressure exerted (in pascal) by a mixture of 3.2 g of methane and 4.4 g of carbon dioxide contained in a 9 dm3 flask at 27°C ?
Answer:

Question 8.
What will be the pressure of the gaseous mixture when 0.5 L of H2 at 0.8 bar and 2.0 L of dioxygen at 0.7 bar are introduced in a 1 L vessel at 27°C ?
Answer:
Step I. Calculation of partial pressure of H2 in 1 L vessel.
V1, = 0-5 L V2 = 1.0 L
P1 = 0.8 bar P2 = ?
According to Boyle’s Law, P1V1 = P2V2
P2 = \(\frac { { P }_{ 1 }{ V }_{ 1 } }{ { V }_{ 2 } } \) = \(\frac { (0.8bar) \times (0.5L) }{ (1.0L) } \) = 0.4bar
Step II. Calculation of partial pressure of O2 in 1 L vessel.
V1 = 2.0 L V2 = 1.0L
P1 = 0.7 bar P2 = ?
According to Boyle’s Law, P1V1 = P2V2
P2 = \(\frac { { P }_{ 1 }{ V }_{ 1 } }{ { V }_{ 2 } } \) = \(\frac { (0.7bar) \times (2.0L) }{ (1.0L) } \) =1.4 bar
Step III. Calculation of total pressure of gaseous mixture.
P = P1 +P2 = (0.4 + 1.4 ) bar = 1.8 bar
Question 9.
The density of a gas is found to be 5.46 g/dm3 at 27°C and under 2 bar pressure. What will be its density at STP ?
Answer:

Question 10.
34.05 mL of phosphorus vapours weigh 0-0625 g at 546°C and 1.0 bar pressure. What is the molar mass of phosphorus ?
Answer:
According to ideal gas equation,
PV = n RT ; PV = \(\frac { WRT }{ M } \) or M = \(\frac { WRT }{ PV } \)
According to available data :
Mass of phosphorus vapours (W) = 0.0625 g
Volume of vapours (V) = 34.05 mL = 34.05 × 103 L
Pressure of vapours (P) = 1.0 bar.
Gas constant (R) = 0.083 bar L K-1 mol-1
Temperature (T) = 546 + 273 = 819 K
![]()
Question 11.
A student forgot to add the reaction mixture to the round bottomed flask at 27°C but put it on the flame. After a lapse of time, he realised his mistake. By using a pyrometer, he found that the temperature of the flask was 477°C. What fraction of air would have been expelled out ?
Answer:
Since the student was working in the laboratory, there is no change in pressure. Thus, Charles’ Law is applicable.
According to given data : V1 = V L (say) V2 = ?
T1 = 27+273 =300 K ; T2 = 477 + 273 = 750K
\(\frac { { V }_{ 1 } }{ { T }_{ 1 } } \) = \(\frac { { V }_{ 2 } }{ { T }_{ 2 } } \) or V2 = \(\frac { { V }_{ 1 }{ T }_{ 2 } }{ { T }_{ 1 } } \) = \frac { (VL)\times (750K) }{ 300K } = 2.5 VL
Thus, volume of air expelled = 2.5 V – V = 1.5 V 1.5V
Fraction of air expelled = \(\frac { 1.5V }{ 2.5V } \) = \(\frac { 3 }{ 5 } \) .
Question 12.
Calculate the temperature of 4.0 moles of a gas occupying 5 dm3 at 3.32 bar (R = 0.083 bar dm3 K-1 mol-1).
Answer:
According to idea gas equation, PV = n RT or T = [/latex] = \(\frac { PV }{ nR } \)
According to available data :
No. of moles of the gas (n) = 4.0 moles
Volume of the gas (V) = 5 dm3
Pressure of the gas (P) = 3.32 bar
Gas constant (R) = 0.083 bar dm3 K-1 mol-1
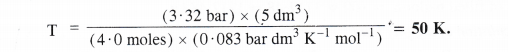
Question 13.
Calculate the total number of electrons present in 1.4 g of nitrogen gas.
Answer:
Molecular mass of N2 = 28g
28g of N2 represent molecules = 6.022 × 1023
1.4 g of N2 represent molecules = 6.022 × 1023 × \(\frac { 1.4g }{ 28g } \) = 3.011 × 1022
Atomic number of nitrogen (N) = 7
1 molecule of N2 has electrones = 7 × 2 = 14
3.011 × 1022 molecules of N2 have electrons = 4 × 3.011 × 1022 = 4.215 × 1023 electrons
Question 14.
How much time would it take to distribute one Avogadro number of wheat grains if 1010 grains are distributed each second ?
Answer:
Time taken to distribute 1010 grains = 1 s

Question 15.
Calculate the total pressure of a mixture of 8 g of oxygen and 4 g of hydrogen confined in a vessel of 1 dm3 at 27°C (R = 0-083 bar dm3K-1mol-1)
Answer:

Question 16.
Pay load is defined as the difference between the mass of displaced air and the mass of the balloon. Calculate the pay load when a balloon of radius 10 m and mass 100 kg is filled with helium at 1.66 bar at 27°C. (Density of air = 1.2 kg m-3 and R = 0.083 bar dm3K-1mol-1).
Answer:
Step I Calculation of the mass of displaced air
Radius of balloon (r) = 10 m
Volume of balloon (V) = \(\frac { 4 }{ 3 } \) πr3 = \(\frac { 4 }{ 3 } \) × \(\frac { 22 }{ 7 } \) × (10 m)3 = 4190.5 m3
Mass of the displaced air = Volume of air (balloon) × Density of air
= (4190.5 m3) × (1.2 kg m-3) = 5028.6 kg
Step II Calculation of the mass of the filled balloon.
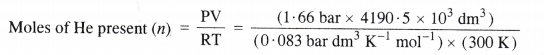
= 279.37 × 103 mol.
Mass of He present = Moles of He × Molar mass of He
= (279.37 × 103 mol) × (4 g mol-1)
= 1117.48 × 103g = 1117.48 kg
Mass of filled balloon = 100 + 1117.48 = 1217.48 kg
Step III. Calcu lation of the pay load
Pay load = Mass of displaced air – Mass of filled balloon
= 5028.6 – 1217.48 =3811.12 kg.
Question 17.
Calculate the volume occupied by 8-8 g of Co2 at 31.1 °C and 1 bar pressure (R = 0.083 bar LK-1mol-1).
Answer:

Question 18.
2.9 g of a gas at 95°C occupied the same volume as 0.184 g of hydrogen at 17°C and at the same pressure. What is the molar mass of the gas ?
Answer:

Question 19.
A mixture of hydrogen and oxygen at one bar pressure contains 20% by weight of hydrogen. Calculate the partial pressure of hydrogen.
Answer:
Let the mass of H2 in the mixture = 20 g
The mass of O2 in the mixture will be = 80 g

Question 20.
What would be SI units of a quantity pV2T2/n ?
Answer:
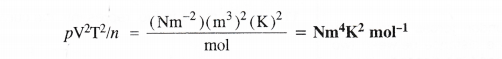
Question 21.
In term of Charles’ Law explain why -273 °C is the lowest possible temperature ?
Answer:
The temperature -273°C (or 0 K) is known as absolute zero temperature. Below this temperature, a substance cannot exist as a gas and changes to the liquid state. This means that the Charles’ Law can be applied only upto a temperature – 273°C since a substance fails to exist as gas below this temperature.
Question 22.
Critical temperature for carbon dioxide and methane are 31.1°C and -81.9°C respectively. Which of these has stronger intermolecular forces and why ?
Answer:
The values of critical temperatures suggest that the attractive forces in the molecules of carbon dioxide are more. In fact, both are non-polar gases but the van der Waals forces of attraction in carbon dioxide molecules are more because of greater molecular size.
Question 23.
Explain the physical significance of van der Waals parameters.
Answer:
Significance and Units of the van der Waals’ constants
The significance and the units of the constant ‘a’ and ‘b’ used in the van der Waals equation are discussed as van der Waals’ constant ‘a’ The constant ‘a’ is related to the magnitude of the attractive forces among the molecules in a particular gas. Thus, greater the value of ‘a’ more will be the attractive forces. It may be noted that ‘a’ is higher for gases like NH3, HCl and SO2 which can be easily liquefied than for gases like He, H2 and N2 which are liquefied with diffieculty. Actually the former are of polar nature and the attractive forces in their molecules are higher than the latter gases which are of non-polar nature. The units of the constant ‘a’ can be calculated as follows :
![]()
Units of ‘a’ are related to the units in which pressure ‘p’ and volume ‘V’ are expressed.
• Pressure is in atmospheres and volume in litres, a = atm. L2 mol-2
• Pressure is in atmospheres and volume in m3, a = atm m6 mol-2
• Pressure is in Nm”2 and volume in m3, a = Nm-2 m6 mol-2
Van der Waals’ constant ‘b’. The constant ‘b’ represents the co-volume or excluded volume which is effective volume of the molecules in a gas. It is, in fact, four times the volume occupied by the gas molecules. The units of ‘h’ can be calculated as follows :
Units of ‘b’ may be L mol-1 or m3 mol-1.
NCERT Solutions for Class 11 Chemistry Chapter 5 States of Matter Solids
These Solutions are part of NCERT Solutions for Class 11 Chemistry. Here we have given NCERT Solutions for Class 11 Chemistry Chapter 5(A) States of Matter Solids.
Question 1.
Define the term ‘amorphous’. Give a few examples of amorphous solids.
Answer:
Amorphous or amorphous solids imply those solids in which the constituent particles have short range order. These have irregular shapes and are isotropic in nature. Apart from that they do not have sharp melting points. A few examples of amorphous solids are : glass, rubber, plastic, celluose etc.
Question 2.
What makes glass different from a solid such as quartz ? Under what conditions could quartz be converted into glass ?
Answer:
Glass is a super cooled liquid and an amorphous substance. Quartz is the crystalline form of silica (SiO2) ‘n which tetrahedral units SiO4 are linked with each other in such a way that the oxygen atom of one tetrahedron is shared with another Si atom. Quartz cap be converted into glass by melting it and cooling the melt very rapidly. In glass, SiO4 tetrahedra are joined in a random manner.
Question 3.
Classify each of the following solids as ionic, metallic, molecular, net work (covalent) or amorphous:
(a) Tetra phosphorus decoxide (P4O10)
(b) Graphite
(c) Brass
(d) Ammonium phosphate (NH4)3PO4
(e) SiC
(f) Rb
(g)I2
(h) LiBr
(i) P4
(j) Si (k) Plastic.
Answer:
(a) Molecular solid
(b) Covalent (Net-work) solid
(c) Metallic solid
(d) Ionic solid
(e) Covalent solid (Network)
(f) Metallic solid
(g) Molecular solid
(h) Ionic solid
(i) Molecular solid
(j) Covalent solid
(k) Amorphous solid
Question 4.
(a)What is meant by the term coordination number ?
(b)What is the co-ordination number of atoms
(i) in a cubic close packed structure
(ii) in a body centred cubic structure ?
Answer:
(a)The co-ordination number of a constituent particle (atom, ion or molecule) is the number of nearest neighbours in its contact in the crystal lattice. „
(b)(i) Twelve, (ii) Eight
Question 5.
How can you determine the atomic mass of an unknown metal if you know its density and dimensions of its unit cell ? Explain your answer.
Answer:
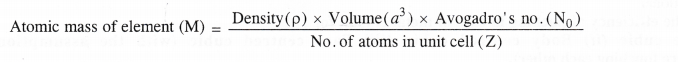
We have learnt that different types of the cubic unit cells differ in their packing fractions i.e. with respect to the the space occupied by the constituting particles. These are expected to differ in their relative densities also. Let us derive a general relation between the edge length and the density in a unit cell.
Consider a unit cell with edge length = a pm = a × 10-10 cm.
(∵ Because density is normally expressed in g cm-3)
Volume of the unit cell = (a × 10-10 cm)3 = a3 × 10-30 cm3
Density of unit cell =\(\frac { Mass\quad of\quad unit\quad cell }{ Volume\quad of\quad unit\quad cell } \) ….(i)
Now, mass of unit cell = No. of atoms in a unit cell × Mass of each atom
Z = \(\frac { Atomic\quad mass\quad (M) }{ Avogadro’s\quad number(No) } \) ….(ii)
By substituting the value of mass of unit cell in equation (i)
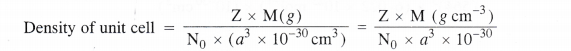
The value of Z is different for different types of cubic unit cells.
It may be noted that the density of any crystalline solid is the same as that of its unit cell.
• While deriving the above relationship, the edge length is expressed in picometre (pm) units. In case, it is expressed in any other units, please convert the same into pm. There is no need to mention its units in the calculations.
Question 6.
(a) Stability of a crystal is reflected in the magnitude of the melting point. Comment.
(b) Collect the melting point of (i) Ice (ii) ethyl alcohol (iii) diethyl ether (iv) methane from a data book. What can you say about intermolecular forces between the molecules ?
Answer:
(a) The stability of a crystal depends upon the magnitude of force of interaction in the constituting particles. Greater the force of attraction present, more will be the stability of the crystal. For example, ionic solids such as NaCl, KC1 etc. have very high melting and boiling points while the molecular crystals such as naphthalene, iodine etc. have low values of melting and boiling points.
(b) The melting points of different substances are :
(i) Ice = 273 K
(ii) Ethyl alcohol = 155.7 K
(iii) Diethyl ether = 156.8 K
(iv) Methane = 90.5 K
The intermolecular forces in molecules of ice and ethyl alcohol are mainly hydrogen bonding. The magnitude is more in ice than in alcohol as is evident from the values of melting points.
The forces in the molecules of diethyl ether are dipolar forces while in methane, these are mainly the van der Waal’s forces which is quite evident from its melting point (least among the compounds listed).
Question 7.
How will you distinguish between the following pairs of terms :
(a) Hexagonal close packing and cubic close packing
(b) Crystal lattice and unit cell
(c) Tetrahedral void and octahedral void.
Answer:
(a) In hexagonal close packing (hep), the spheres of the third layer are vertically above the spheres of the first layer
(ABABAB type). On the other hand, in cubic close packing (ccp), the spheres of the fourth layer are present
above the spheres of the first layer (ABCABC type).
(b) Crystal Lattices and Unit Ceils
We have studied that in the crystalline solids, the constituent particles (atoms, ions or molecules) have a regular orderly arrangement throughout and it gets repeated again and again resulting in a definite pattern. These points are generally shown as dots (.) and the sites which are occupied by these points are known as lattice sites or crystal lattices. Crystal lattices may be either two dimensional or three dimensional in nature.
Two dimensional crystal lattices : A two dimensional lattice is planar and is represented in terms of two basic vectors (a and b) and the angle (L) between them. There are five different types of two dimensional lattices :
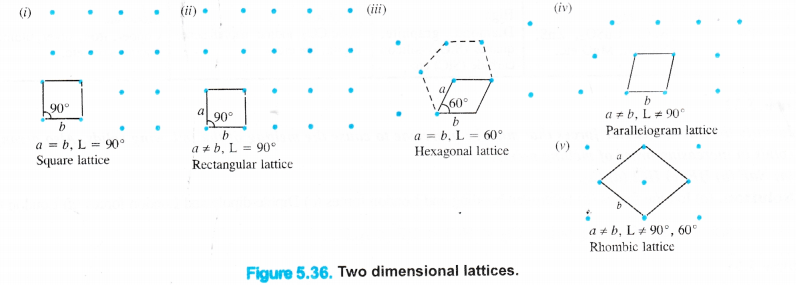
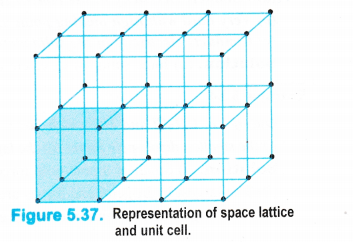
Three dimensional crystal lattices : A three dimensional lattice is a further extension of the two dimensional lattice. It depicts the actual shape as well as size of the constituent particles in the crystal.
It is therefore, called space lattice or cyrstal lattice. It may be defined as :
the regular three dimensional arrangement of the points in a crystal.
Please note that
• Each point in the lattice is known as lattice point or lattice site.
• Each point in the lattice represents the constituting particle. These particles may be atoms, ions or molecules depending upon the nature of the crystalline solid.
• Lattice points are joined by straight lines in order to depict the geometry of the solid. A typical space lattice has been shown in the fig. 5.37.
Unit Cell
If we carefully examine the space lattice given in the figure, we can find a group of lattice points (shown as shaded) which get repeated in different directions to form the complete lattice. This smallest repeating pattern is called unit cell which may be defined as :
the smallest but complete unit in the space lattice which when repeated over and again in the three dimensions, generates the crystal of the given substance.
In order to illustrate a unit cell, let us consider a block made of bricks of the same size. Each brick represents the unit cell while the block is similar to the space or crystal lattice. Thus, a unit cell is the fundamental building block of the space lattice.
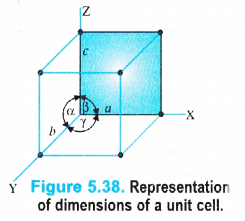
It may be noted that crystals differ from each other with respect to the shape and size of the unit cells. A unit cell is completely characterised in terms of edge lengths and the angles between the edges.
(i) Edges or edge lengths. The edges a, b and c represent the dimensions of the unit cell in space along the three axes. The edges may or may not be mutually perpendicular.
(ii) Angles between the edges. There are three angles between the edges. These are denoted as \(\alpha \) (between b and c), \(\beta \) (between a and c) and \(\Upsilon \) (between a and b). Thus, a unit cell may be characterised by six parameters as shown in the Fig. 5.38. The various types
of crystal systems differ with respect to edge lengths as well as angles between the edges.
(c) Tetrahedral and Octahedral Voids or Interstitial Sites
In the discussion about the close packing of spheres in space, we have seen that even in the closest packed structure when the spheres (or particles) touch each other, certain space in between the particles is left unoccupied. For example, in both hep and ccp, 26% of the space is left unoccupied. In fact, the spheres can touch each other only at certain points. The space which is left in between the closest packed arrangement is known as void, hole or interstice. Two types of voids or interstitial sites are formed in close packed structures. These are tetrahedral and octahedral voids.
Tetrahedral Voids.
We have seen that a triangular void is formed in hexagonal two dimensional close packing . A tetrahedral void is formed when the triangular void made by three spheres of a particular layer and touching each other has a contact with one sphere either in the upper layer or the layer below it. Thus, a tetrahedral void is formed when four spheres placed at the comers of a tetrahedron touch each other as shown in the Figure 5.54.
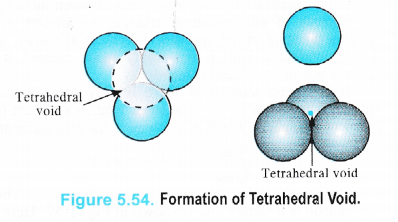
It is interesting to note that the actual shape of the void is triangular but the arrangement of the spheres around the void is tetrahedral.
In a close packed structure, each sphere is in contact with three spheres in the layer above it and also three spheres in the layer below it. Thus, there are two tetrahedral voids associated with each sphere (or constituting particle). The radius of a tetrahedral void in a closest packed structure is 22.5% of the sphere which is involved in the arrangement. Thus,
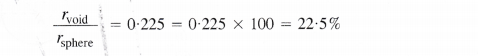
Octahedral Voids
An octahedral void or site is formed when three spheres arranged at the corners of an equilateral triangle are placed over another set of spheres pointing in the opposite directions as shown in the Figure 5.56.
Thus, octahedral void is the empty space created at the centre of six spheres which are. placed octahedrally.
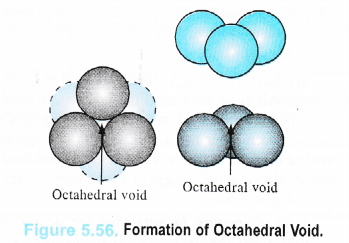
It has been found that there is only one octahedral site for each sphere. The radius of an octahedral void in a closest packed structure is 0.414 of the sphere which is involved in the arrangement.
![]()
Question 8.
How many lattice points are there in one unit cell of each of the following lattices
(a) face centred cubic (b) face centred tetragonal (c) body centred cubic ?
Answer:
(a) In face centred cubic arrangement,
Lattice points located at the corners of the cube = 8
Lattice points located at the centre of each face = 6
Total no. of lattice points = 8 + 6 = 14
(b) In face centred tetragonal, the number of lattice points is also the same i.e., 8 + 6 = 14.
(In both the cases, .particles per unit cell = 8 × \(\frac { 1 }{ 8 } \) + 6 × \(\frac { 1 }{ 2 } \) – 4)
(c) In body centred cubic arrangement,
Lattice points located at the corners of the cube = 8
Lattice points located in the centre of the body = 1
Total no. of lattice points =8+1=9
(the total number of particles per unit cell = 8 × \(\frac { 1 }{ 8 } \) + 1 = 2)
Question 9.
Explain :
(i) The basis of similarities and differences between metallic and ionic crystals.
(ii) Ionic solids are hard and brittle.
Answer:
(i) Basis of similarities. The basis of similarities between the metallic and ionic crystals are the presence of strong electrostatic forces of attraction. These are present among the ions in the ionic crystals and among the kernels and valence electrons in the metallic crystals. That is why both metals and ionic compounds are good conductors of electricity and have high melting points.
Basis of differences. The basis of differences is the absence of mobility of ions in the ionic crystals while the same is present in the valence electrons and kernels in case of metallic crystals. As a consequence, the ionic compounds conduct electricity only in the molten state while the metals can do so even in the solid state.
(ii) The ionic solids are hard and brittle because of strong electrostatic forces- of attraction which are present in the oppositely charged ions.
(iii) The ionic solids are hard because of the presence of strong inter ionic forces of attraction in the oppositely charged ions. These ions are arranged in three dimensional space. The ionic solids are brittle because the ionic bond is non-directional.
Question 10.
Calculate the efficiency of packing in case of metal crystal for :
(i) Simple cubic
(ii) Body centred cubic
(iii) Face centred cubic (with the assumption that the atoms are touching each other).
Answer:
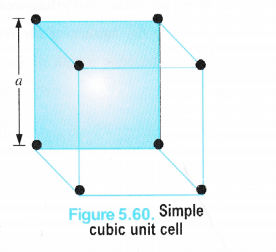
(i) Simple Cubic Unit Cell
We have calculated the number of atoms or spheres (since an atom or particle may be regarded as the sphere) in different types of cubic unit cells. Now, let us calculate the relation between the edge length (a) and the radius (r) of the spheres present in these unit cells in case of pure elements i.e. elements composed of the same type of atoms.
It may be noted that :
(a) Distance between the centres of the spheres present on the corners of the edges of the cube is called edge length (a).
(b) Distance between the centres of the two nearest spheres is called nearest neighbour
distance (d) and is equal to r + r = 2r. (Here r is the radius of the spheres or the atomic radius.) .
We know that in a simple cubic unit cell, there is one atom (or one sphere) per unit cell. If r is the radius of the sphere, volume occupied by one sphere present in the unit cell = \(\frac { 4 }{ 3 } \) πr3.
Since the spheres at the corners touch each other ; Edge length (a) = r + r = 2r = d
(ii) Body Centred Cubic Unit Cell
We know that a body-centred cubic unit cell has 2 spheres (atoms) per unit cell. If r is the radius of the sphere Volume of one sphere = 4/3 nr3
Volume of two spheres present in the unit cell = \(\frac { 4 }{ 3 } \) πr3 × 2 = \(\frac { 8 }{ 3 } \) πr3</sup .
From the Fig. 5.62, it is evident that the sphere present in the centre of the cube touches a corner sphere so that the distance in their centres = 2r
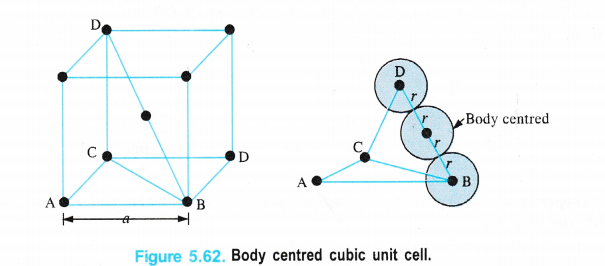
Length of the body diagonal (BD) in the cube = 4r.
By considering the triangle BCD and by applying Pythagorean theorem,
BD2 = CD2 + BC2
But BC2 = AB2 + AC2
∴ BD2 = CD2 + AB2 + AC2
edge length = a, then
(4r)2 = a2 + a2 + a2
16r2 = 3a2 or a = (16/3 r2)1/2
a = \(\frac { 4r }{ \sqrt { 3 } } \) or r = \(\frac { \sqrt { 3 } a }{ 4 } \)
or d = 2r = \(\frac { 2\times \sqrt { 3 } a }{ 4 } \) = \(\frac { \sqrt { 3 } a }{ 2 } \)
(iii)Face centred cubic unit cell
We know that a face centred cubic unit cell (fcc) contains four spheres (or atoms) per unit cell.
The spheres at the corners are touching the sphere or atom present in the centre. However, they can not touch each other.
Figure 5.61, Faced centred cubic unit cell.
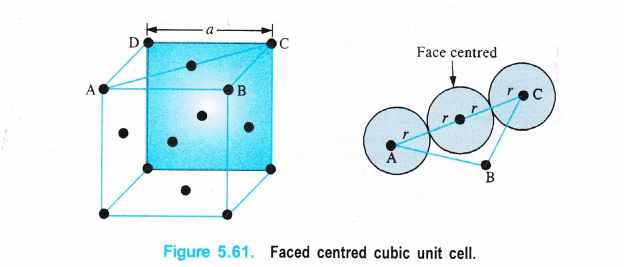
Volume occupied by one sphere of radius r = \(\frac { 4 }{ 3 } \) πr3
∴ Volume occupied by four spheres present in the unit cell = \(\frac { 4 }{ 3 } \) πr3 × 4 = \(\frac { 16 }{ 3 } \) πr3
Distance in their centres = r + r = 2r
Length of the face diagonal = r + 2r + r = 4r.
Now, according to Pythagorean theorem,
the square of the hypotenuse of a right triangle is equal to sum of the squares of the other two sides. If a is the edge length of the unit cell, then
a2 + a2 = (4r)2 or 2a2 = 16r2
a2 = \(\frac { 16 }{ 2 } \) r2 = 8r2 or a = (8r2)1/2 = \(\sqrt { 8 } \)r
a = 2r\(\sqrt { 2 } \) or r = \(\frac { a }{ 2\sqrt { 2 } } \)
d = 2r = \(\frac { 2a }{ 2\sqrt { 2 } } \) = \(\frac { a }{ \sqrt { 2 } } \) (d is the nearest neighbour distance.)
Question 11.
Silver crystallises in a face centred cubic lattice with all the atoms at the lattice points. The length of the edge of the unit cell as determined by X-ray diffraction studies is found to be 4.077 × 10-8 cm. The density of silver is 10.5 g cm-3. Calculate the atomic mass of silver.
Answer:
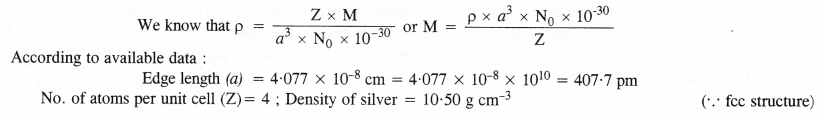
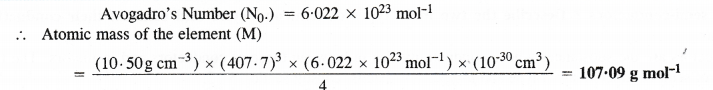
Question 12.
A cubic solid is made of two elements P and Q. Atoms Q are at the corners of the cube and P at the body centre. What is the formula of the compound ? What is the co-ordination number of P and Q ?
Answer:
Contribution by atoms Q present at the eight comers of the cube = \(\frac { 1 }{ 8 } \) × 8 = 1
Contribution by atom P present at the body centre = 1
Thus, P and Q are present in the ratio 1:1.
∴ Formula of the compound is PQ.
Co-ordination number of atoms P and Q = 8.
Question 13.
Niobium crystallises in body centred cubic structure. If the density is 8.55 g cm-3, calculate atomic radius of niobium given that atomic mass of niobium is 93 g mol-1.
Answer:

Question 14.
If the radius of octahedral void is r and the radius of the atom in close packing is R, derive the relation between r and R.
Answer:
A tetrahedral void has been shown in the Figure 1.54. Here three spheres form the triangle base while the fourth sphere lies at the top. The shaded sphere occupies the tetrahedral void. Let the radii of void and sphere be r and R respectively. Let the edge length of the cube be a.
From the right hand triangle ABC,
AB2 = AC2 + BC2
Here AB is the face diagonal while AC and BC are the edge lengths (a). Therefore,
AB2 = a2 + a2
or AB = (2a2) 1/2= a\(\sqrt { 2 } \)

Question 15.
Copper crystallises into a fee lattice with edge length 3.61 × 10-8 cm. Show that the calculated density is in agreement with its measured value of 8.92 g cm-3.
Answer:
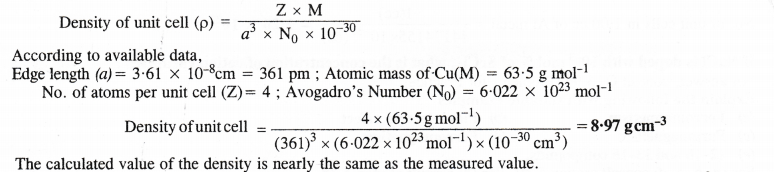
Question 16.
Analysis shows that nickel oxide has formula Ni0.98 O1.00. What fraction of nickel exists as Ni2+ and as Ni3+ ions ?
Answer:
The ratio of Ni and O atoms in pure nickel oxide (NiO) = 1 : 1
Let x be the no. of Ni (II) atoms replaced by Ni (III) atoms in the oxide.
∴ No. of Ni (II) atoms present = (0.98 – x)
Since the oxide is neutral in nature,
Charge on Ni atoms = Charge on oxygen atoms
2(0.98 -x) + 3x =2
1.96 – 2x + 3x =2
x = 2 – 1.96 = 0.04
% of Ni (III) atoms in nickel oxide \(\frac { No.of\quad Ni(III)atoms }{ Total\quad no.Ni\quad atoms } \) × 100 = \(\frac { 0.04 }{ 0.98 } \) = 4.01%
% of Ni (II) atoms in nickel oxide = 100 – 4.01 = 95.99%
Question 17.
What are semi-conductors ? Describe the two main types of semiconductors and contrast their conduction mechanisms.
Answer:
Semi-conductors are the substances whose conductivity lies in between those of conductors and insulators. The two main types of semi-conductors are n-type and p-type.
Applications of n-type and p-type semi-conductors
Germanium and silicon are the elements which belong to group 14 and have four valence electrons in their atoms. These are both metalloids and also semi-conductors. A large variety of solid state materials have been prepared by the combination of elements belonging to group 13 and 15 or group 12 and 16. These have also four valence electrons. A few examples of compounds resulting from 13-15 combination are : InSb, A1P and GaAs. Similarly, compounds resulting from 12-16 combination are CdS, CdSe, HgTe. (Cd and Hg are the transition metals present in group 12). These have resulted in many sophisticated semi-conductors which have brought about a revolution in this field.
If a single crystal is doped with indium at one end and with arsenic at the other end, then one part is a p-type semi¬conductor while the other is «-type semi-conductor. In the middle, the region where the two sides meet represents n-p junction These junctions are used in making microcompressor devices and integrated circuits in the solid state electronics.
Some important applications of n- and p-type semi-conductors are listed.
1. Rectifiers : The role of rectifiers is to allow current from an outside source to flow in one direction and thus, converts an alternate current (AC) into direct current. For this, a circuit made from four diodes is needed. A diode is basically a transistor consisting of two zones ; one p-type and the other n-type along with a n-p junction in between.
2. Photovoltaic cells : A photovoltaic cell is a device which can convert light energy into electrical energy. In order to achieve this, a n-p junction is irridiated with photons of light having energy more than band gap. As a result, some n-p bonds break and generate electrons and positive holes. These electrons then get promoted from valence band to the conduction band. These extra electrons present in the conduction band make the n-type region more negative. At the same time in the p-type region, the electrons get trapped by some positive holes. By connecting the two regions in the external circuit, the electrons are in a position to flow from n-type region to the p-type region. The current flows in the opposite direction i.e., from p-type region to the n-type region. In this manner, photo-voltaic cells function. As pointed earlier, they work at the expense of light energy into electrical energy.
3. Transistors : These are basically single crystals of silicon which have been doped to give three zones i.e., p-n-p and n-p-n. These transistors have wide range of applications. They work as amplifiers and oscillators in radios, televisions and also in computers. In addition, these are used as photo-transistors, tunnel diodes, solar cells etc. Now-a-days, it has become possible to manufacture computer chips which are equivalent to many thousand single crystal transistors.
Question 18.
Non-stoichiometric cuprous oxide (Cu2O) can be prepared in the laboratory. In this oxide, copper to oxygen ratio is slightly less than 2:1. Can you account for the fact that this substance is a p-type semi-conductor ?
Answer:
The ratio less than 2 : 1 in Cu20 shows that some cuprous (Cu+) ions have been replaced by cupric (Cusup>2+) 10ns. In order to maintain the electrical neutrality, every two Cusup>+ ions will be replaced by one Cusup>2+ ion which results in creating cation vacancies leading to positive holes. Since the conduction is due to positive holes, it is a p-type semiconductor.
Question 19.
Ferric oxide crystallises in a hexagonal close packed array of oxide ions with two out of every three octahedral holes occupied by ferric ions. Derive the formula of ferric oxide.
Answer:
There is one octahedral hole for each atom in hexagonal close packed arrangement.
If the number of oxide ions (O2-) per unit cell is 1, then the number of Fe3+ ions = \(\frac { 2 }{ 3 } \) × octahedral holes = \(\frac { 2 }{ 3 } \) ×1 = 2/3. Thus, the formula of the compound = Fe2/3O1 or Fe2C3.
Question 21.
Gold (atomic radius = 0.14411m) crystallises in a face centred unit cell. What is the length of the side of the unit cell ?
Answer:
For a face centred cubic unit cell (fcc)
Edge length (a) = 2\(\sqrt { 2r } \) = 2 × 1.4142 × 0.144 mm = 0.407 nm
Question 22.
In terms of Band Theory, what is the difference (i) between a conductor and an insulator (ii) between a conductor and semi-conductor ?
Answer:
Explanation for Conductors, Insulators and Semi-conductors
The’variation in the electrical conductivity of the solids can be explained with the help of the band theory. In metals, the energy gap between the partially filled valence band and unoccupied conduction band is negligible. Rather they overlap and electron flow readily takes place. In semi-conductors, there is small energy gap between valence band and conduction band. However, some electrons may jump to the conduction band and these semi-conductors can exhibit a little electrical conductivity.
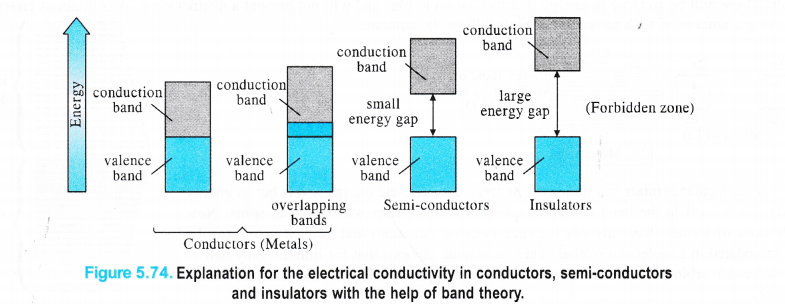
For example, in case of silicon and germanium, these are 111 kJ mol-1 and 63 kJ mol-1 respectively and the electron jump is feasible. The conductivity of the semi-conductors increases with the rise in temperature because more electrons are now in a position to jump from the valence band to the conduction band. Such type of semi-conductors are known as intrinsic semiconductors However, the conductivity of these semi-conductors is so low that it is hardly useful practically. In insulators, the energy gaps are very large and the no electron jump is feasible from the valence band to the conduction band. The energy gaps also called forbidden zones. The insulators therefore, do not conduct electricity. For example, in case of diamond the energy gap is of the order of 5 IT kJ mol-1. Therefore, diamond is an insulator. From the above discussion, we conclude that the conductivity in the solids is primarily linked with the energy difference between the valence and conduction bands.
Question 23.
Explain the following terms with suitable examples.
(i) Schottky defect, (ii) Frenkel defect, (iii) Interstitials, (iv) F-centres.
Answer:
(i) Schottky defect. The defect was noticed by German scientist Schottky in 1930. This arises because certain ions are missing from the crystal lattice and vacancies or holes are created at their respective positions. Since a crystal is electrically neutral, the number of such missing cations (A+) and anions (B–) must be the same. The crystal lattice of an ideal crystal and that sufferring from Schottky defect has been shown below. Only one cation and one anion have been indicated as missing.
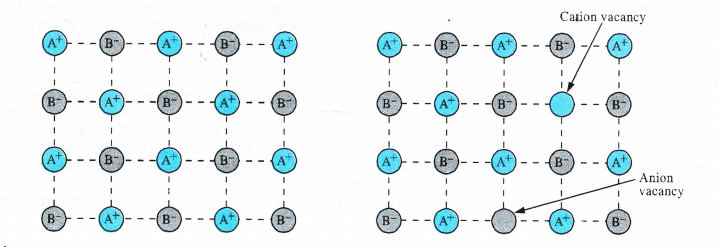
These are only the planar representation of the crystal lattice and not the three dimensional or space lattice.
(ii) Frenkel Defect. This defect in the ionic crystals was discovered by a Russian scientist Frenkel in 1926. It results when certain ions leave their normal sites and occupy positions elsewhere in the crystal lattice. Holes are created at their respective positions. Since cations are smaller in size as compared to anions normally these are involved in Frenkel defect.
Frenkel defect is depicted in the Fig. 5.67 in which only one cation has been shown to be dislocated from its position.
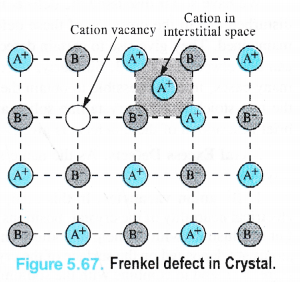
(iii)Interstitial defect. This defect is noticed when certain constituent particles (atoms or molecules) occupy the interstitial sites in the crystal lattice.. As a result, the number of particles per unit volume increases and so is the density of the solid. These defects are very common in the interstitial compounds of transtion metals. For details, consult unit 8 (d and fblock elements).
Question 24.
Aluminium crystallises in a cubic close packed structure. Its metallic radius is 125 pm.
(a) What is the length of the side of the unit cell ?
(b) How many unit cells are there in 1-00 cm3 of aluminium ?
Answer:
Step I. Calculation of length of side of the unit cell
Forf.c.c. unit cell, a = 2\(\sqrt { 2r } \) = 2\(\sqrt { 2 } \)(125pm) = 2 × 1.4142 × (125 pm) = 354 pm.
Step II. Calculation of no. of unit cells in 1.00 cm3 of aluminium.
Volume of one unit cell = (354 pm)3 = (354 x 10-10 cm)3 = 44174155 × 10-30 cc.
No. of unit cells in 1.00 cc of Al metal = \(\frac { 1(cc) }{ 44174155\times { 10 }^{ -30 }(cc) } \) = 2.26 x 1022.
Question 25.
If NaCl is doped with 10-3 mol % of SrCl2, what is the concentration of cation vacancies ?
Answer:
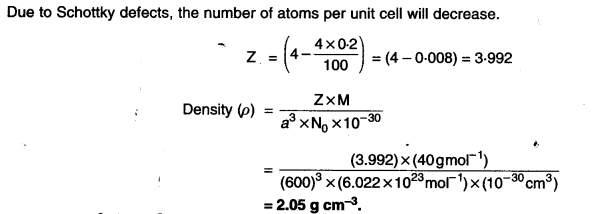
Question 26.
Explain the following with suitable examples
(a) Ferromagnetism (b) Piezoelectric effect
(c) Paramagnetism (d) Ferromagnetism
(e) 12-16 and 13-15 compounds.
Answer:
(a)Ferromagnetic solids (Ferromagnetism). A few solids like iron, cobalt, nickel, gadolinium and Cr02 are attracted very strongly by magnetic fields. These are known as ferromagnetic solids. Apart from that, they can be even permanently magnetised or become permanent magnet. Actually, in the solid state, the metal ions of these substances are grouped together into small regions known as domains. Each domain behaves like a small magnet. When a ferromagnetic solid is placed in a magnetic field, all the domains get oriented in the direction of the magnetic field (Fig. 5.76 (a)). As a result, a strong magnetic effect is produced. The effect persists even when the magnetic field is removed. Thus, a ferromagnetic substance becomes a permanent magnet. CrO2 is used in magnetic tapes for audio frequency.
(b) Piezoelectric effect. It may be noted that all the three types of solids (ferromagnetic, anti-ferromagnetic and ferrimagnetic) listed above may become paramagnetic upon heating upto a certain temperature known as Curie temperature. The change in the magnetic character is because of the reallignment of the magnetic moments or domains in one direction upon heating.For example,
(i) Ferricmagnetic solid Fe3O4 becomes paramagnetic when heated to 850 K.
(ii) Antiferromagnetic solid V2O3 becomes paramagnetic when heated to 750 K.
(c) Paramagnetic solids (Paramagnetism). These are the solids attracted by a magnet and this property is known as paramagnetism. Actually, the atoms of the elements present have certain unpaired electrons. Their spins or magnetic moments may lead to magnetic character. However, the electron spins may mutually cancel due to random orientation under normal conditions and the substances may not have any magnetic character. Under the influence of an external magnetic field or magnet, the spins of certain electrons may allign to produce temporary magnetism i.e. they may be attracted by the magnet. However, they may lose their orientation and also magnetic character once the magnet is removed. This means that their magnetic character is temporary and is present as long as external magnetic field is present. Many transition metals such as Co, Ni, Fe, Cu, etc. and their ions are paramagnetic. Similarly, dioxygen (O2) and nitric oxide (NO) have also unpaired electrons and they exhibit paramagnetism.
(d).Ferrimagnetic solids (Ferrimagnetism). In certain ferromagnetic solids, the magnetic moment of the domains allign in parallel and anti-parallel directions in unequal numbers as shown in the Fig. 5.76(c). As a result, they-‘have certain resultant magnetic moment or magnetic character which is of permanent nature. However, ferrimagnetic solids are less magnetic than ferromagnetic solids. For example, magnetic oxide of iron (Fe3O4) and ferrites with general formula MFe2O4 (where M = Mg, Cu, Zn etc.) are ferrimagnetic in nature.

We hope the NCERT Solutions for Class 11 Chemistry at Work Chapter 5 States of Matter help you. If you have any query regarding NCERT Solutions for Class 11 Chemistry at Work Chapter 5 States of Matter Solids, Liquids and Gases, drop a comment below and we will get back to you at the earliest.
Class 11 Chemistry NCERT Solutions
- Some Basic Concepts of Chemistry Class 11 NCERT Solutions
- Structure of Atom Class 11 NCERT Solutions
- Classification of Elements and Periodicity in Properties Class 11 NCERT Solutions
- Chemical Bonding and Molecular Structure Class 11 NCERT Solutions
- States of Matter Class 11 NCERT Solutions
- Thermodynamics Class 11 NCERT Solutions
- Equilibrium Class 11 NCERT Solutions
- Redox Reactions Class 11 NCERT Solutions
- Hydrogen Class 11 NCERT Solutions
- The s Block Elements Class 11 NCERT Solutions
- The p Block Elements Class 11 NCERT Solutions
- Organic Chemistry: Some Basic Principles and Techniques Class 11 NCERT Solutions
- Hydrocarbons Class 11 NCERT Solutions
- Environmental Chemistry Class 11 NCERT Solutions