RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7
These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7
Other Exercises
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.9
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.11
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables VSAQS
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables MCQS
Question 1.
The sum of two numbers is 8. If their sum is four times their difference, find the numbers.
Solution:
Let first number = x
and second number = y
x + y = 8 ….(i)
and x + y = 4 (x – y)
=> 4 (x – y) = 8
=> x – y = 2 ….(ii)
Adding (i) and (ii),
2x = 10 => x = 5
Subtracting (ii) from (i),
2y = 6 => y = 3
Numbers are 5, 3
Question 2.
The sum of digits of a two digit number is 13. If the number is subtracted from the one obtained by interchanging the digits, the result is 45. What is the number ?
Solution:
Let unit’s digit = x
and ten’s digit = y
Number = x + 10y
Now according to the condition
x + y = 13 ….(i)
Number after interchanging their digits,
y + 10x
Now y + 10x – x – 10y = 45
9x – 9y = 45
=> x – y = 5
x – y = 5 ….(ii)
Adding (i) and (ii),
2x = 18 => x = 9
subtracting 8
2y = 8 => y = 4
Number = x + 10y = 9 + 4 x 10 = 9 + 40 = 49
Question 3.
A number consists of two digits whose sum is five. When the digits are reversed, the number becomes greater by nine. Find the number.
Solution:
Let units digit = x
and ten’s digit = y
Number = x + 10y
and number by reversing their digits = y+ 10x
Now according to the conditions,
x + y = 5 ….(i)
and y + 10x = x + 10y + 9
=> y + 10x – x – 10y = 9
=> 9x – 9y = 9x – y = 1 ….(ii)
(Dividing by 9)
Adding we get:
2x = 6 => x = 3
and subtracting,
2y = 4 => y = 2
Number = x + 10y = 3 + 10 x 2 = 3 + 20 = 23
Question 4.
The sum of digits of a two digit number is 15. The number obtained by reversing the order of digits of the given number exceeds the given number by 9. Find the given number. (C.B.S.E. 2004)
Solution:
Let the ones digit = x
and tens digit = y
Number = x + 10y
and number by reversing the order of digits = y +10x
According to the conditions,
x + y = 15 ….(i)
y + 10x = x + 10y + 9
=> y + 10x – x – 10y = 9
=> 9x – 9y = 9
=>x – y = 1 ……..(ii)
(Dividing by 9)
Adding (i) and (ii)
2x = 16
x = 8
and subtracting, 2y = 14 => y = 7
Number = x + 10y = 8 + 10 x 7 = 8 + 70 = 78
Question 5.
The sum of a two-digit number and the number formed by reversing the order of digits is 66. If the two digits differ by 2, find the number. How many such numbers are there ? [NCERT]
Solution:
Sum of two-digit number and number formed by reversing its digits = 66
Let units digit = x
Then tens digit = x + 2
Number = x + 10 (x + 2) = x + 10x + 20 = 11x + 20
and by reversing its digits
Unit digit = x + 2
and tens digit = x
Number = x + 2 + 10x = 11x + 2
11x + 20 + 11x + 2 = 66
=> 22x + 22 = 66
=> 22x = 66 – 22 = 44
=> x = 2
Number = 11x + 20 = 11 x 2 + 20 = 22 + 20 = 42
and number by reversing its digits will be 11x + 2 = 11 x 2 + 2 = 22 + 2 = 24
Hence numbers are 42 and 24
Question 6.
The sum of two numbers is 1000 and the difference between their squares is 256000. Find the numbers.
Solution:
Let first number = x
and second number = y
x + y = 1000 ……..(i)

Question 7.
The sum of a two digit number and the number obtained by reversing the order of its digits is 99. If the digits differ by 3, find the number. (C.B.S.E. 2002)
Solution:
Let the unit’s digit of the number = x
and ten’s digit = y
Number = x + 10y
By reversing the digits, the new number will be = y +10x
According to the condition,
x + 10y + y + 10x = 99
=> 11x + 11y = 99
=> x + y = 9 ….(i)
and x – y = 3 ….(ii)
Adding we get,
2x = 12
x = 6
and subtracting, 2y = 6
y= 3
Number = x + 10y = 6 + 10 x 3 = 6 + 30 = 36
Question 8.
A two-digit number is 4 times the sum of its digits. If 18 is added to the number, the digits are reversed. Find the number. (C.B.S.E. 2001C)
Solution:
Let the unit digit of the number = x
and tens digit = y
Number = x + 10y
and number after reversing the order of digits = y + 10x
According to the conditions,
x + 10y = 4 (x + y)
=> x + 10y = 4x + 4y
=> 4x + 4y – x – 10y = 0
=> 3x – 6y = 0
=> x – 2y = 0
=> x = 2y ….(ii)
and x + 10y + 18 = y + 10x
=> x + 10y – y – 10x = -18
=> – 9x + 9y = -18
=> x – y = 2 ….(ii)
(Dividing by – 9)
=> 2y – y = 2 {From (i}
=> y = 2
x = 2y = 2 x 2 = 4
Number = x + 10y = 4 + 10 x 2 = 4 + 20 = 24
Question 9.
A two-digit number is 3 more than 4 times the sum of its digits. If 18 is added to the number, the digits are reversed. Find the number. (C.B.S.E. 2001C)
Solution:
Let unit digit of the number = x
and ten’s digit = y
Number = x + 10y
and number after reversing the digits = y + 10x
According to the conditions,
x + 10y = 4 (x + y) + 3
=> x + 10y = 4x + 4y + 3
=> x + 10y – 4x – 4y = 3
=> -3x + 6y = 3
=> x – 2y = -1 ….(i)
(Dividing by -3)
and x + 10y + 18 = y + 10x
=> x + 10y – y – 10x = -18
=> -9x + 9y = -18
=>x – y = 2 ….(ii)
(Dividing by 9)
Subtracting (i) from (ii)
y = 3
x – 3 = 2
=>x = 2 + 3 = 5 {From (ii)}
Number = x + 10y = 5 + 10 x 3 = 5 + 30 = 35
Question 10.
A two digit number is 4 more than 6 times the sum of its digits. If 18 is subtracted from the number, the digits are reversed. Find the number. (C.B.S.E. 2001C)
Solution:
Let units digit of the number = x
and ten’s digit = y
then number = x + 10y
The number by reversing the digits = y+ 10x
According to the condition given,
x + 10y = 6 (x + y) + 4
=> x + 10y = 6x + 6y + 4
=> x + 10y – 6x – 6y = 4
=> -5x + 4y = 4 ….(i)
and x + 10y – 18 = y + 10x
=> x + 10y – y – 10x = 18
=> -9x + 9y = 18
=> x – y = -2 ….(ii)
(Dividing by 9)
=> x = y – 2
Substituting in (i),
-5 (y – 2) + 4y = 4
-5y + 10 + 4y = 4
-y = 4 – 10 = – 6
y = 6
Number = x + 10y = 4 + 10 x 6 = 4 + 60 = 64
Question 11.
A two-digit number is 4 times the sum of its digits and twice the product of the digits. Find-the number. (C.B.S.E. 2005)
Solution:
Let the units digit of the number = x
and tens digit = y
Number = x + 10y
According to the conditions given,
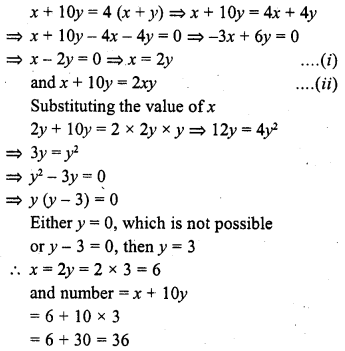
Question 12.
A two-digit number is such that the product of its digits is 20. If 9 is added to the number, the digits interchange their places. Find the number. (C.B.S.E. 2005)
Solution:
Let the units digit of the number = x
and tens digit = y
Number = x + 10y
and number after interchanging its digits = y + 10x
According to the conditions,
xy = 20

Question 13.
The difference between two pumbers is 26 and one number is three times the other. Find them.
Solution:
Let first number = x
and second number = y
x – y = 26 ……….(i)
x = 3y ….(ii)
Substituting the value of x in (i)
3y – y = 26
=> 2y = 26
=>y = 13
x = 3y = 3 x 13 = 39
Numbers are 39, 13
Question 14.
The sum of the digits o,f a two-digit number is 9. Also, nine times this number is twice the number obtained by reversing the order of the digits. Find the number.
Solution:
Let the units digit of the number = x
and tens digit number = y
Number = x + 10y
and the number by reversing the order of the digits = y + 10x
According to the condition;
x + y = 9 …..(i)
9 (x + 10y) = 2 (y + 10x)
=> 9x + 90y = 2y + 20x
=> 9x + 90y – 2y – 20x = 0
=> -11x + 88y = 0
=> x – 8y = 0 (Dividing by -11)
=> x = 8y
Substituting the value of x in (i)
8y + y = 9
=> 9y = 9
=> y= 1
x = 8y = 1 x 8 = 8
Number = x + 10y = 8 + 10 x 1 = 8 + 10 = 18
Question 15.
Seven times a two-digit number is equal to four times the number obtained by reversing the digits. If the difference between the digits is 3. Find the number.
Solution:
Let the units digit of the number = x
and tens digit = y
Number = x + 10y
and number after reversing the digits = y + 10x
According to the conditions,
x – y = 3 ….(i)
and 7 (x + 10y) = 4 (y + 10x)
=> 7x + 70y = 4y + 40x
=> 7x + 70y – 4y – 40x = 0
=> -33x + 66y = 0
=> x – 2y = 0 (Dividing by -33)
=> x = 2y
Substituting the value of x in (i),
2y – y = 3 => y = 3
x = 2y = 2 x 3 = 6
and number = x + 10y = 6 + 10 x 3 = 6 + 30 = 36
Question 16.
Two numbers are in the ratio 5 : 6. If 8 is subtracted from each of the numbers, the ratio becomes 4 : 5. Find the numbers. [NCERT Exemplar]
Solution:
Let the two numbers be x and y.
Then, by the first condition, ratio of these two numbers = 5 : 6
x : y = 5 : 6
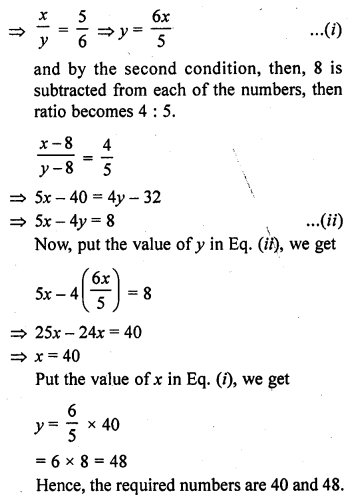
Question 17.
A two-digit number is obtained by either multiplying the sum of the digits by 8 and then subtracting 5 or by multiplying the difference of the digits by 16 and then adding 3. Find the number. [NCERT Exemplar]
Solution:
Let the two-digit number = 10x + y
Case I : Multiplying the sum of the digits by 8 and then subtracting 5 = two-digit number
=> 8 x (x + y) – 5 = 10x + y

Hope given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.