RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10
These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10
Other Exercises
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.9
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.11
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables VSAQS
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables MCQS
Question 1.
Points A and B are 70 km. a part on a highway. A car starts from A and another car starts from B simultaneously. If they travel in the same direction, they meet in 7 hours, but if they travel towards each other, they meets in one hour. Find the speed of the two cars. (C.B.S.E. 2002)
Solution:
Distance between two points A and B = 70 km
Let speed of first car starting from A = x km/hr
and speed of second car starting from B =y km/hr
When these start in the some direction, they meet after 7 hours
Distance travelled by the first car = 7x km
and by second car = 7y km

When these travel in opposite direction, they meet after 1 hour then distance travelled by first car = x km
and by second car = y km
x + y = 70 ….(ii)
Adding (i) and (ii)
2x = 80
=> x = 40
and subtracting (i) from (ii)
2y = 60
=> y = 30
Speed of first car = 40 km/hr
and speed of second car = 30 km/hr
Question 2.
A sailor goes 8 km downstream in 40 minutes and returns in 1 hour. Determine the speed of the sailor in still water and the speed of the current. (C.B.S.E. 1997)
Solution:
Let the speed of sailor in still water = x km/ hr
and speed of water = y km/hr
Distance covered = 8 km

Question 3.
The boat goes 30 km upstream and 44 km downstream in 10 hours. In 13 hours, it can go 40 km upstream and 55 km downstream. Determine the speed of stream and that of the boat in still water.
Solution:
Let the speed of stream = y km/hr
and speed of boat = x km/hr
Speed of boat downstream = (x + y) km/hr
In first case, and up stream = (x – y) km/hr
Upstream distance = 30 km
and down distance = 44 km
Total time taken = 10 hrs
In second case,
upstream distance = 40 km
and downstream distance = 55 km
Total time taken = 13 hrs
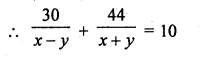
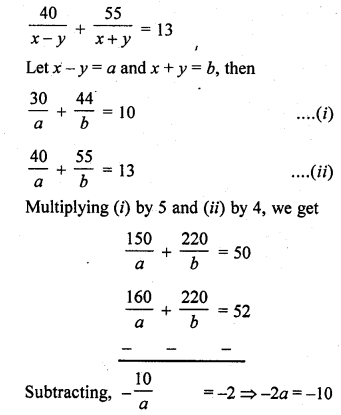
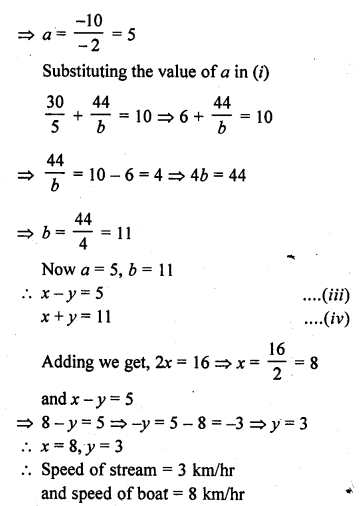
Question 4.
A boat goes 24 km upstream and 28 km downstream in 6 hrs. It goes 30 km upstream and 21 km downstream in 6\(\frac { 1 }{ 2 }\) hrs. Find the speed of the boat in still water and also speed of the stream.
Solution:
Let the speed of boat = x km/hr
and speed of stream = y km/hr
In first case,
Distance covered upstream = 24 km
and down stream = 28 km
Total time taken = 6 hours
In second case,
Distance covered upstream = 30 km
and downstream = 21 km
Total time taken = 6\(\frac { 1 }{ 2 }\) = \(\frac { 13 }{ 2 }\) hrs.
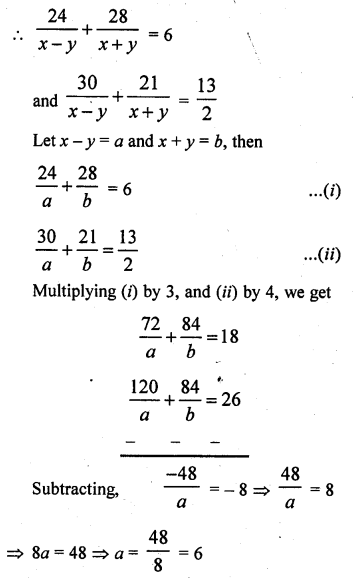
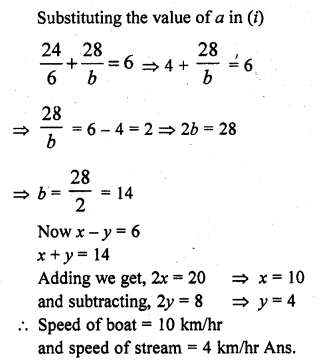
Question 5.
A man walks a certain distance with a certain speed. If he walks 1/2 km an hour faster, he takes 1 hour less. But, if he walks 1 km an hour slower, he takes 3 more hours. Find the distance covered by the man and his original rate of walking.
Solution:
Let the distance = x km
and let certain speed = y km/hr
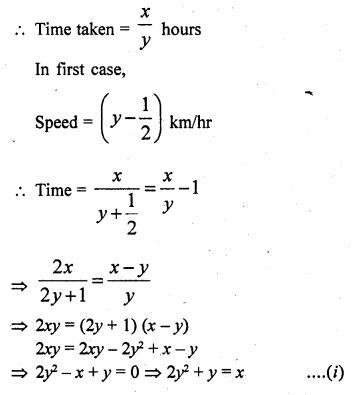
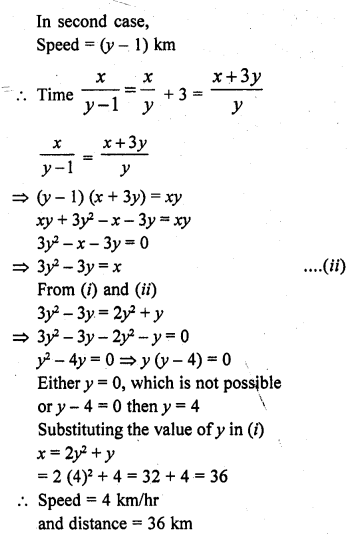
Question 6.
A person rowing at the rate of 5 km/h in still water, takes thrice as much time in going 40 km upstream as in going 40 km downstream. Find the speed of the stream. [NCERT Exemplar]
Solution:
Let the speed of the stream be v km/h
Given that, a person rowing in still water = 5 km/h
The speed of a person rowing in downstream = (5 + v) km/h
and the speed of a person Has rowing in upstream = (5 – v) km/h
Now, the person taken time to cover 40 km downstream,


Question 7.
Ramesh travels 760 km to his home partly by train and partly by car. He takes 8 hours if he travels 160 km. by train and the rest by car. He takes 12 minutes more if the travels 240 km by train and the rest by car. Find the speed of the train and car respectively.
Solution:
Total distance = 769 km
Let the speed of train = x km/hr
and speed of car = y km/hr
Time taken = 8 hours
In first case, distance travelled by train = 160 km
and rest distance 760 – 160 = 600 km by car
Time taken


Question 8.
A man travels 600 km partly by train and partly by car. If the covers 400 km by train and the rest by car, it takes him 6 hours and 30 minutes. But, if he travels 200 km by train and the rest by car, he takes half an hour longer. Find the speed of the train and that of the car. (C.B.S.E. 2001)
Solution:
Total journey = 600 km
Let the speed of train. = x km/hr
and speed of car = y km/hr
In first case,
Journey by train = 400 km
Journey by car = 600 – 400 = 200 km



Question 9.
Places A and B are 80 km apart from each other on a highway. A car starts from A and other from B at the same time. If they move in the same direction, they meet in 8 hours and if they move in opposite directions, they meet in 1 hour and 20 minutes. Find the speeds of the cars. [CBSE 2002]
Solution:
Distance between A and B = 80 km
One car starts from A and other from B in the same direction and they meet after 8 hours
Let the speed of the first car = x km/hr
and speed of second car = y km/hr
Distance travelled by the first car = 8x km
and by the second car = 8y km
8x – 8y = 80
=> x – y = 10 ….(i)
When the two cars move in opposite direction, they

Question 10.
A boat goes 12 km upstream and 40 km downstream in 8 hours. It can go 16 km upstream and 32 km downstream in the same time. Find the speed of the boat in still water and the speed of the steam. [CBSE 1999C]
Solution:
Let the speed of boat = x km/hr
and speed of stream = y km/hr
=> Speed of the boat upstream = (x – y) km/hr
and speed of boat down stream = x + y km/ hr
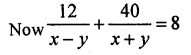
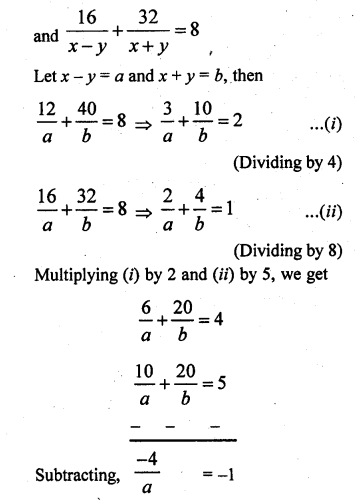
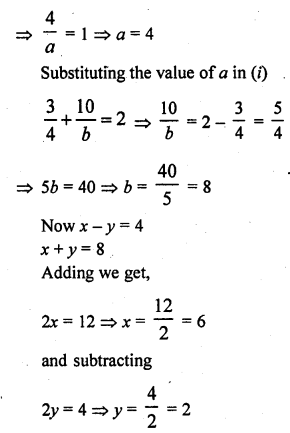
Hence speed of boat = 6 km/hr and speed streams = 2 km/hr
Question 11.
Roohi travels 300 km to her home partly by train and partly by bus. She takes 4 hours if she travels 60 km by train and the remaining by bus. If she travels 100 km by train and the remaining by bus, she takes 10 minutes longer. Find the speed of the train and the bus separately.
Solution:
Total distance = 300 km
Let the speed of train = x km/hr
and speed of bus = y km/hr
In first case,
Distance travelled by train = 60 km
and distance by bus = 300 – 60 = 240
and total time taken = 4 hrs
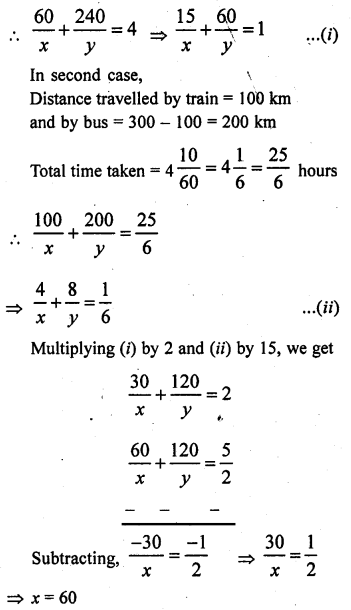

Question 12.
Ritu can row downstream 20 km in 2 hours and upstream 4 km in 2 hours. Find her speed of rowing in still water and the speed of the current.
Solution:
Let the speed of rowing in still water = x km/hr
and speed of current of water = y km/hr
Speed of downstream = (x + y) km/hr
and speed of upstream = (x – y) km/hr
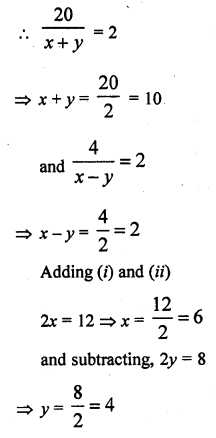
Speed of rowing = 6 km/hr and speed of current = 4 km/hr
Question 13.
A motor boat can travel 30 km upstream and 28 km downstream in 7 hours. It can travel 21 km upstream and return in 5 hours. Find the speed of the boat in still water and the speed of the stream. [NCERT Exemplar]
Solution:
Let the speed of the motorboat in still water and the speed of the stream are u km/h and v km/h, respectively.
Then, a motorboat speed in downstream = (u + v) km/h
and a motorboat speed in upstream = (u – v) km/h
Motorboat has taken time to travel 30 km upstream,

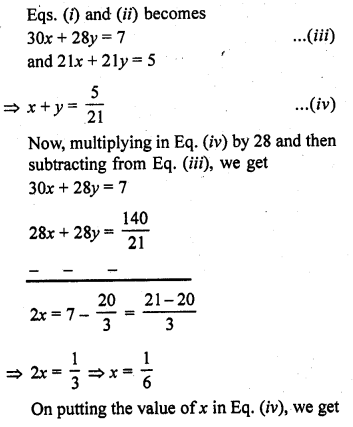
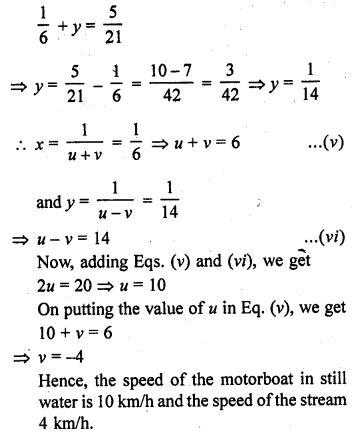
Question 14.
Abdul travelled 300 km by train and 200 km by taxi, it took him 5 hours 30 minutes. But it he travels 260 km by train and 240 km by taxi he takes 6 minutes longer. Find the speed of the train and that of the taxi. (CBSE 2006C)
Solution:
Let the speed of train = x km/hr
and speed of taxi = y km/hr
In first case,
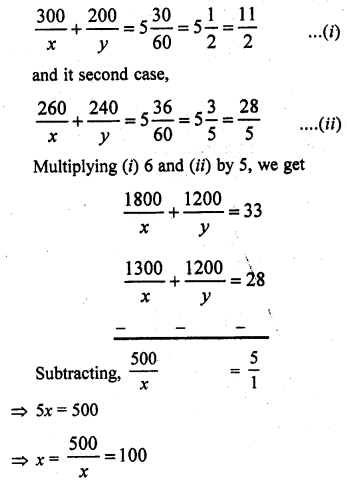

Question 15.
A train covered a certain distance at a uniform speed. If the train could have been 10 km/hr. faster, it would have taken 2 hours less than the Scheduled time. And, if the train were slower by 10 km/ hr ; it would have taken 3 hours more than the scheduled time. Find the distance covered by the train.
Solution:
Let the speed of the train = x km/hr
and time taken = y hours
Distance = speed x time = x x y = xy km
In the first case,
Speed = (x + 10) km/hr
Time = (y – 2) hours
Distance = (x + 10) (y – 2) = xy
=> xy – 2x+ 10y – 20 = xy
=> -2x + 10y – 20 = 0
=> x – 5y + 10 = 0 ……….(i)
In second case,
Speed of the train = (x – 10) km/hr
and time = (y + 3) hours
Distance = (x – 10) (y + 3) = xy
=> xy + 3x – 10y – 30 = xy
=> 3x – 10y – 30 = 0 ………(ii)
Multiplying (i) by 2 and (ii) by 1

Question 16.
Places A and B are 100 km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 5 hours. If they travel towards each other, they meet in 1 hour. What are the speeds of two cars ?
Solution:
Distance between A and B places = 100 km
Let the speed of first car (starting from A) = x km/hr
and speed of second car (starting from B) = y km/hr
In first case, when the cars travel in the same direction
Time when they meet = 5 hours
Distance travelled by first car in 5 hours = 5x km
and by second car = 5y = 5y km
5x – 5y = 100
=> x – y = 20 …(i)
In second case, when the cars travel in the opposite direction
Time when they meet = 1 hour
Distance travelled by first case = x x 1 = x km
and by second car = y x 1 = y km
x + y = 100 ……..(i)
Adding (i) and (ii)
2x = 120 => x = 60
Subtracting (i) from (ii)
2y = 80 => y = 40
Speed of first car = 60 km/hr and speed of second car = 40 km/hr
Question 17.
While covering a distance of 30 km. Ajeet takes 2 hours more than Amit. If Ajeet doubles his speed, he would take 1 hour less than Amit. Find their speeds of walking.
Solution:
Total distance = 30 km
Let speed of Ajeet = x km/hr
and speed of Amit = y km/hr
Now according to the condition,
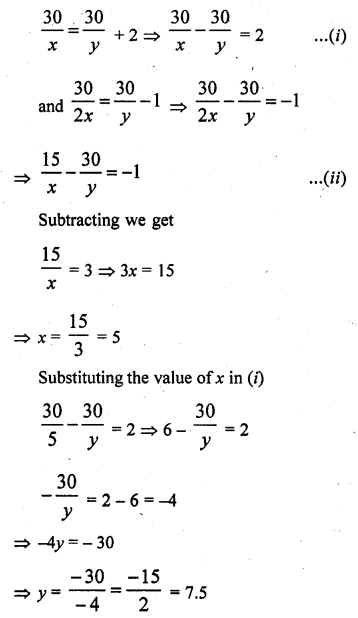
Speed of Ajeet = 5 km/hr and speed of Amit = 7.5 km/hr
Question 18.
A takes 3 hours more than B to walk a distance of 30 km. But if A doubles his pace (speed) he is ahead of B by 1\(\frac { 1 }{ 2 }\) hours. Find their speeds.
Solution:
Let speed of A = x km/hr
and speed of B = y km/hr
Total distance in first case,
\(\frac { 30 }{ x }\) – \(\frac { 30 }{ y }\) = 3
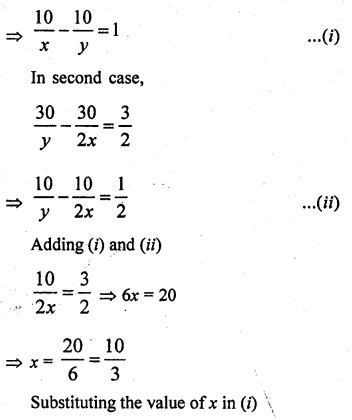
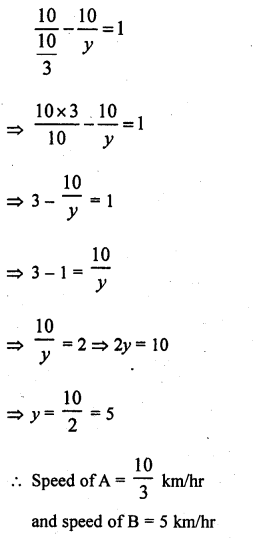
Hope given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.