RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5
These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5
Other Exercises
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.9
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.11
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables VSAQS
- RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables MCQS
In each of the following systems of equations determine whether the system has a unique solution, no solution or infinitely many solutions. In case there is a unique solution, find it : (1 – 4)
Question 1.
x – 3y = 3
3x – 9y = 2 (C.B.S.E. 1994)
Solution:
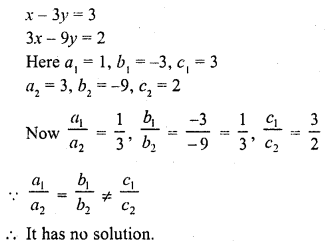
Question 2.
2x + y = 5
4x + 2y = 10 (C.B.S.E. 1995C)
Solution:
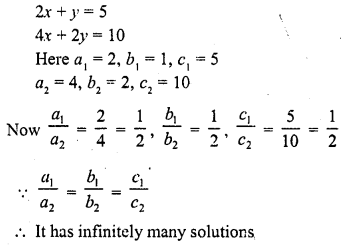
Question 3.
3x – 5y = 20
6x – 10y = 40 (C.B.S.E. 1993)
Solution:
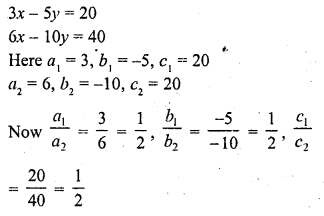
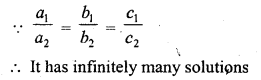
Question 4.
x – 2y = 8
5x – 10y = 10 (C.B.S.E. 1993)
Solution:
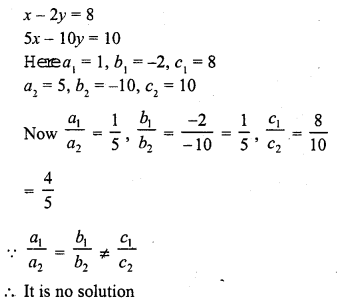
Find the value of k for which the following system of equations has a unique solution: (5 – 8)
Question 5.
kx + 2y = 5
3x + y = 1 (C.B.S.E. 1990C, 92C)
Solution:
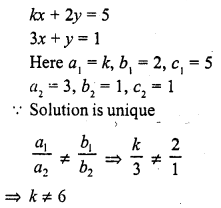
Question 6.
4x + ky + 8 = 0
2x + 2y + 2 = 0 [NCERT]
Solution:
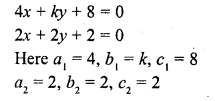
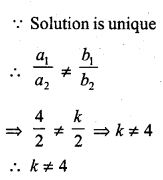
Question 7.
4x – 5y = k
2x – 3y = 12
Solution:
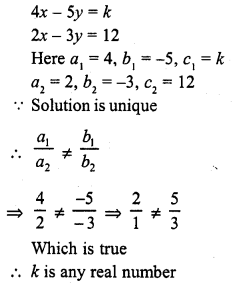
Question 8.
x + 2y = 3
5x + ky + 7 = 0
Solution:
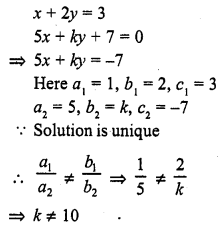
Find the value of k for which each of the following systems of equations have infinitely many solution : (9 – 19)
Question 9.
2x + 3y – 5 = 0
6x + ky – 15 = 0 (C.B.S.E. 1991)
Solution:
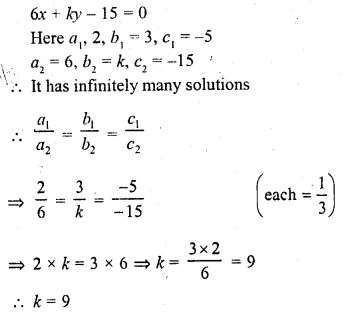
Question 10.
4x + 5y = 3
kx + 15y = 9 (C.B.S.E. 1990C)
Solution:
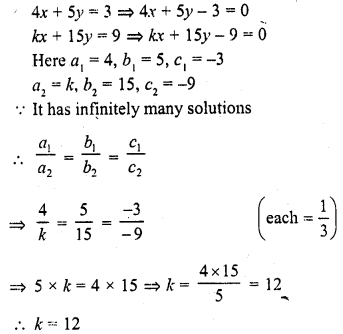
Question 11.
kx – 2y + 6 = 0
4x – 3y + 9 = 0
Solution:
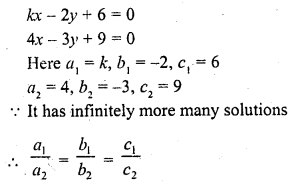
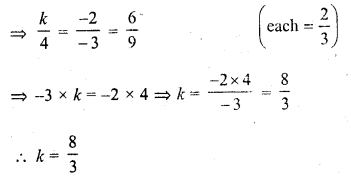
Question 12.
8x + 5y = 9
kx + 10y = 18 (C.B.S.E. 1999)
Solution:
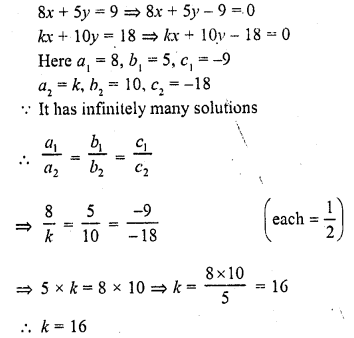
Question 13.
2x – 3y = 7
(k + 2) x + (2k + 1) y = 3 (2k – 1) (C.B.S.E. 1999)
Solution:
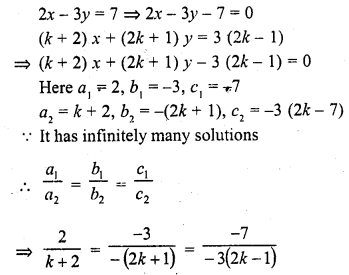
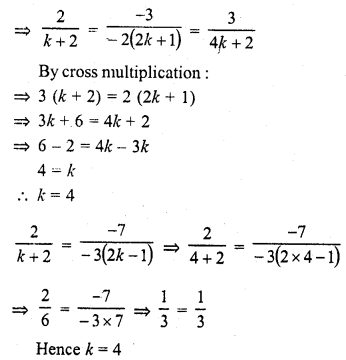
Question 14.
2x + 3y = 2
(k + 2)x + (2k + 1) y = 2 (k – 1) (C.B.S.E. 2000, 2003)
Solution:
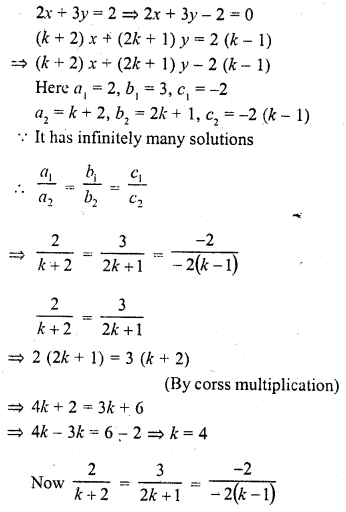
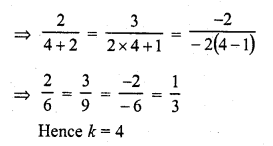
Question 15.
x + (k + 1) y = 4
(k + 1) x + 9y = 5k + 2 (C.B.S.E. 2000C)
Solution:
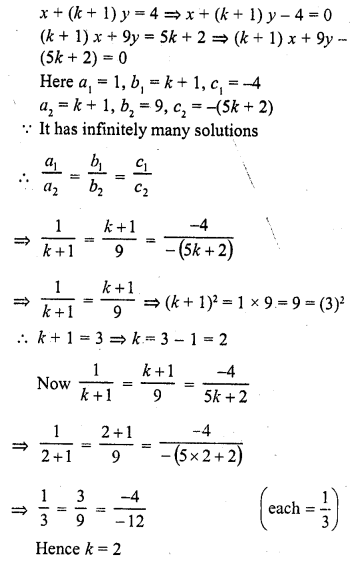
Question 16.
kx + 3y = 2k + 1
2(k+ 1) x + 9y = 7k + 1 (C.B.S.E. 2000C)
Solution:
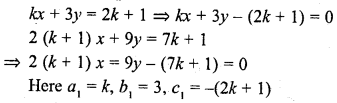
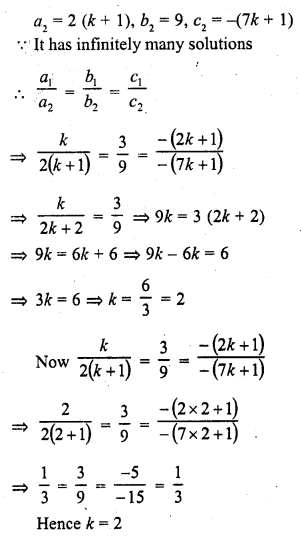
Question 17.
2x + (k – 2) y = k
6x + (2k – 1) y = 2k + 5 (C.B.S.E. 2000C)
Solution:
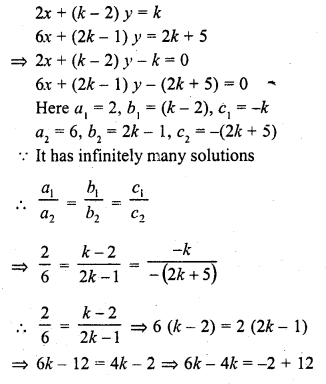
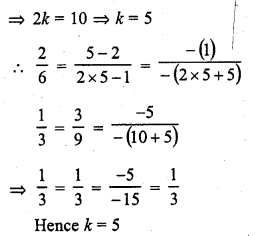
Question 18.
2x + 3y = 7
(k + 1) x + (2k – 1)y = 4k + 1 (C.B.S.E. 2001)
Solution:
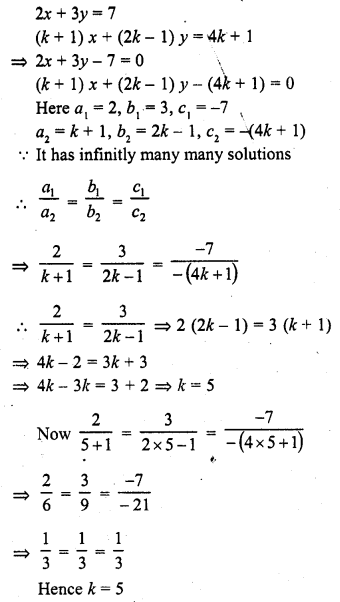
Question 19.
2x + 3y = k
(k – 1) x + (k + 2) y = 3k (C.B.S.E. 2001)
Solution:
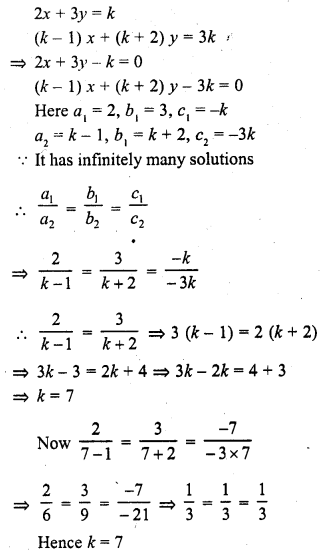
Find the value of k for which the following system of equations has no solution : (20 – 25) :
Question 20.
kx – 5y = 2
6x + 2y = 1 (C.B.S.E. 1994C)
Solution:
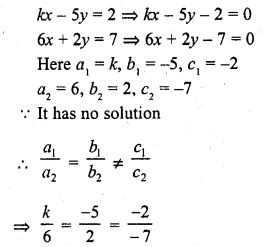
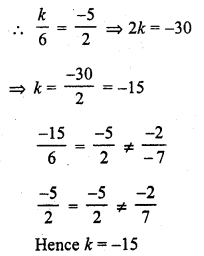
Question 21.
x + 2y = 0
2x + ky = 5 (C.B.S.E. 1993C)
Solution:
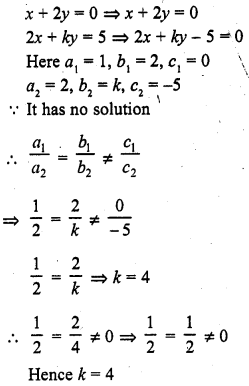
Question 22.
3x – 4y + 7 = 0
kx + 3y – 5 = 0 (C.B.S.E. 1996)
Solution:
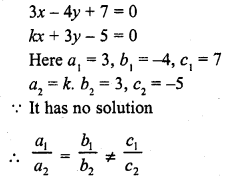
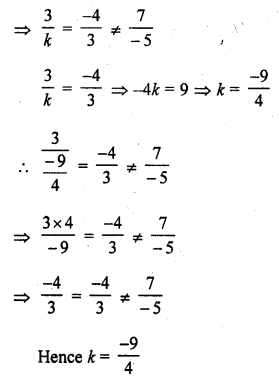
Question 23.
2x – ky + 3 = 0
3x + 2y – 1 = 0 (C.B.S.E. 1996)
Solution:
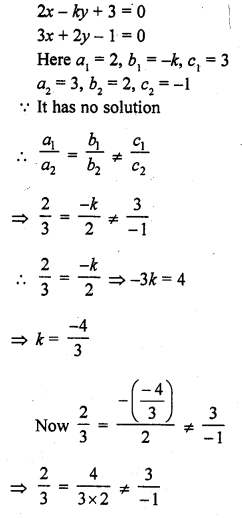
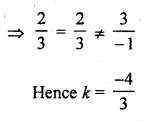
Question 24.
2x + ky = 11
5x – 7y = 5 (C.B.S.E. 1995)
Solution:
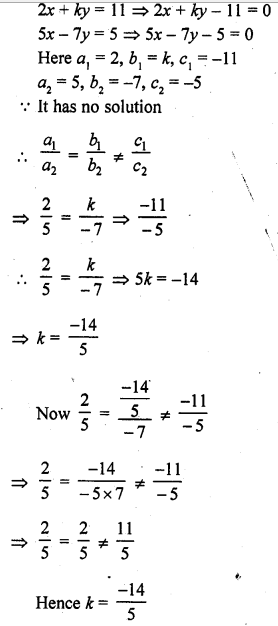
Question 25.
kx + 3y = 3
12x + ky = 6
Solution:
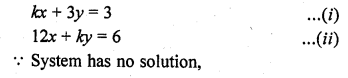
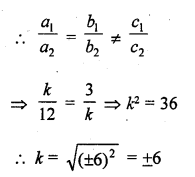
Question 26.
For what value of k, the following system of equations will be inconsistant ?
4x + 6y = 11
2x + ky = 1 (C.B.S.E. 1994C)
Solution:

Question 27.
For what value of a, the system of equations
αx + 3y = α – 3
12x + αy = α
will have no solution. (C.B.S.E. 2003)
Solution:
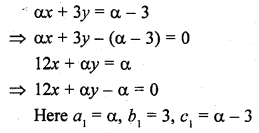
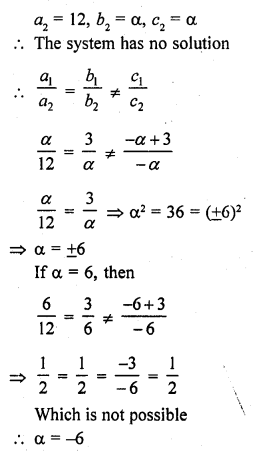
Question 28.
Find the value of k for which the system
kx + 2y = 5
3x + y = 1
has (i) a unique solution, and (ii) no solution.
Solution:

k = 6
Question 29.
Prove that there is a value of c (≠ 0) for which the system
6x + 3y = c – 3
12x + cy = c
has infinitely many solutions. Find this value.
Solution:
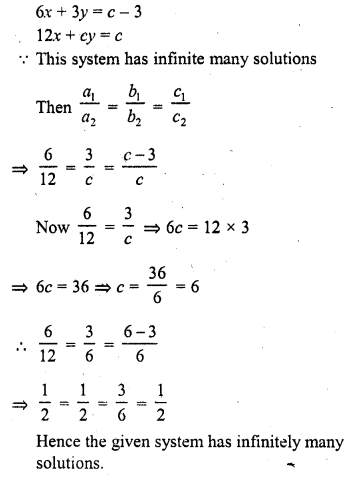
Question 30.
Find the values of k for which the system
2x + k y = 1
3x – 5y = 7
will have (i) a unique solution, and (ii) no solution.
Is there a value of k for which the system has infinitely many solutions?
Solution:
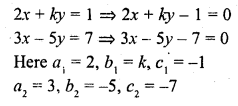
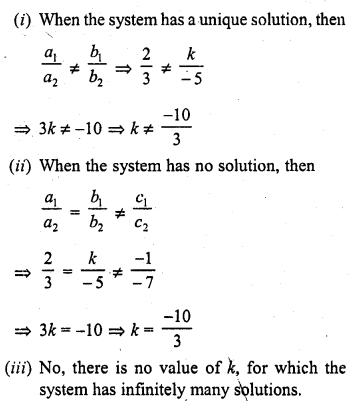
Question 31.
For what value of k, the following system of equations will represent the coincident lines ?
x + 2y + 7 = 0
2x + ky + 14 = 0 (C.B.S.E. 1992)
Solution:
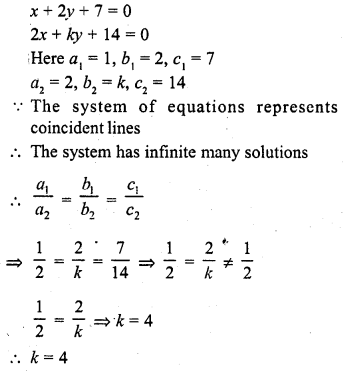
Question 32.
Obtain the condition for the following system of linear equations to have a unique solution
ax + by = c
lx + my = n (C.B.S.E. 1991C)
Solution:
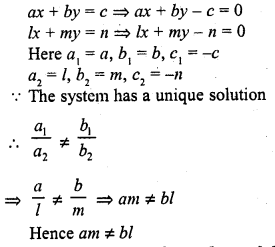
Question 33.
Determine the values of a and b so that the following system of linear equations have infinitely many solutions ?
(2a – 1) x + 3y – 5 = 0
3x + (b – 1) y – 2 = 0 (C.B.S.E. 2001C)
Solution:
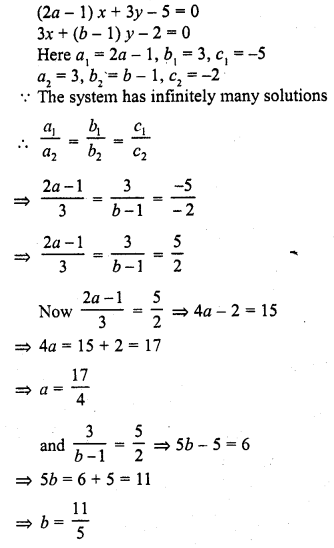
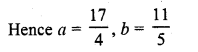
Question 34.
Find the values of a and b for which the following system of linear equations has infinite number of solutions :
2x – 3y = 7
(a + b) x – (a + b – 3) y = 4a + b (C.B.S.E. 2002)
Solution:
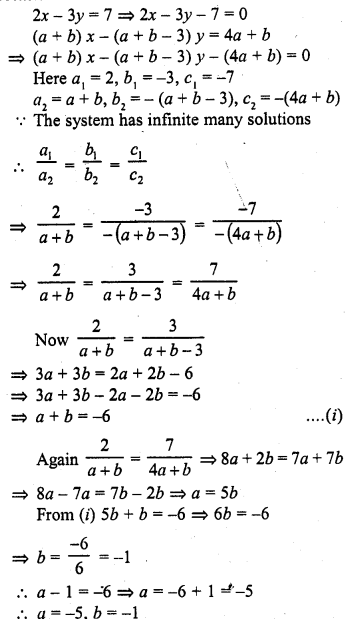
Question 35.
Find the values of p and q for which the following system of linear equations has infinite number of solutions:
2x + 3y = 9
(p + q) x + (2p – q) y = 3 (p + q + 1)
Solution:
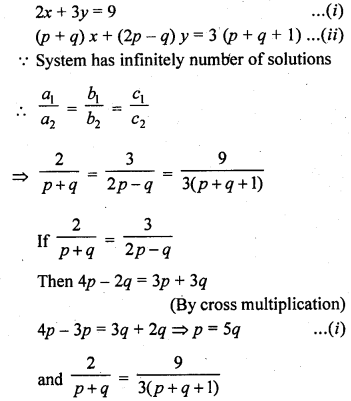
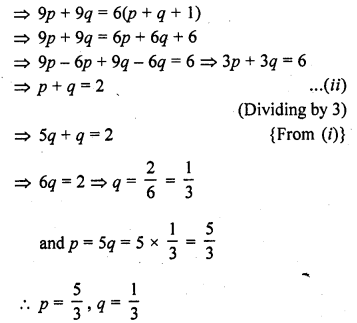
Question 36.
Find the value of a and b for which the following system of equations has infinitely many solutions :
(i) (2a – 1) x – 3y = 5
3x + (b – 2) y = 3 (C.B.S.E. 2002C)
(ii) 2x – (2a + 5) y = 5
(2b + 1) x – 9y = 15 (C.B.S.E. 2002C)
(iii) (a – 1) x + 3y = 2
6x + (1 – 2b) y = 6 (C.B.S.E. 2002C)
(iv) 3x + 4y = 12
(a + b) x + 2 (a – b) y = 5a – 1 (C.B.S.E. 2002C)
(v) 2x + 3y = 7
(a – b) x + (a + b) y = 3a + b – 2
(vi) 2x + 3y – 7 = 0 [CBSE 2010]
(a – 1) x + (a + 1) y = (3a – 1)
(vii) 2x + 3y = 7
(a – 1) x + (a + 2) y = 3a [CBSE 2010]
(viii) x + 2y = 1
(a – b) x + (a + b) y = a + b – 2 [NCERT Exemplar]
(ix) 2x + 3y = 7
2ax + ay = 28 – by [NCERT Exemplar]
Solution:
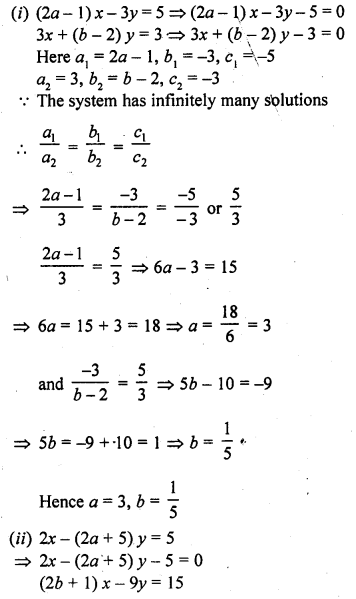
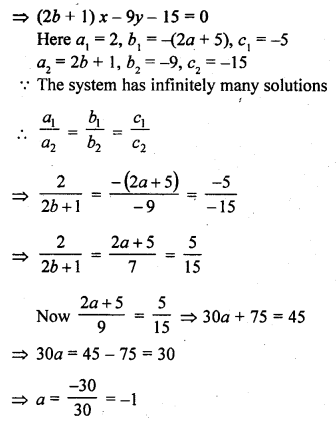
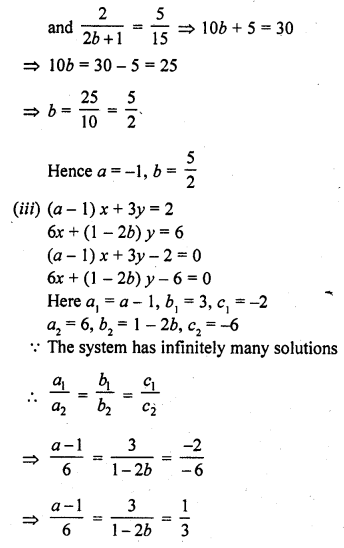
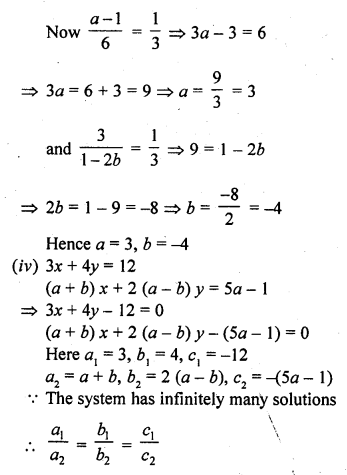
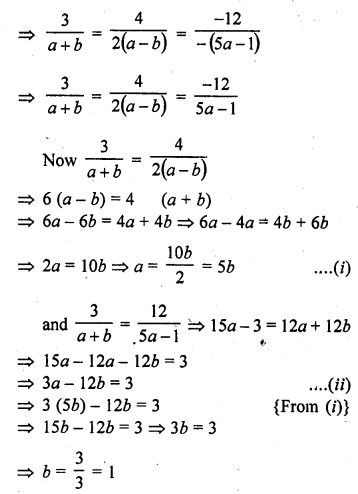
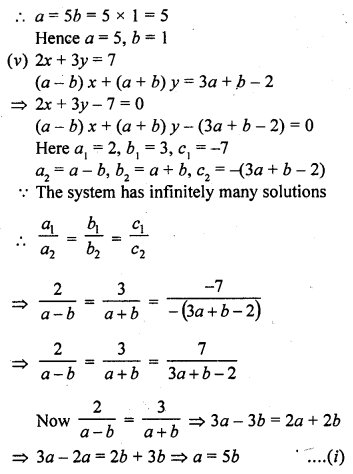
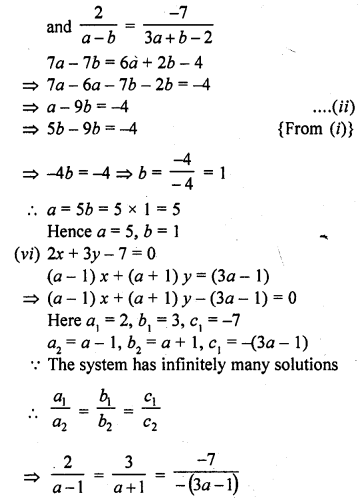
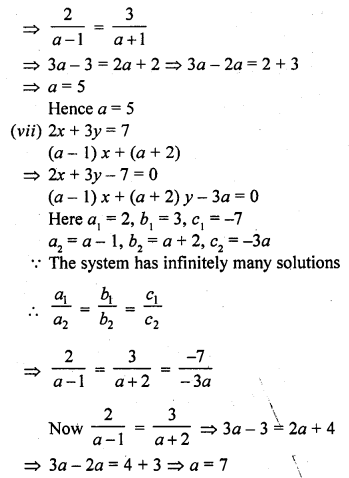
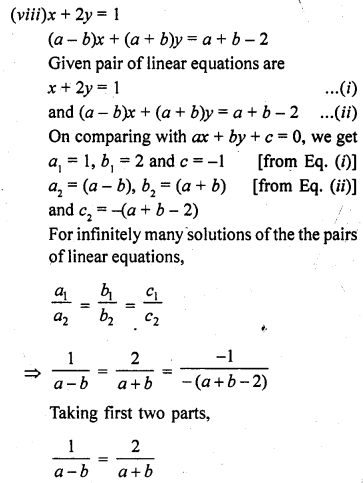
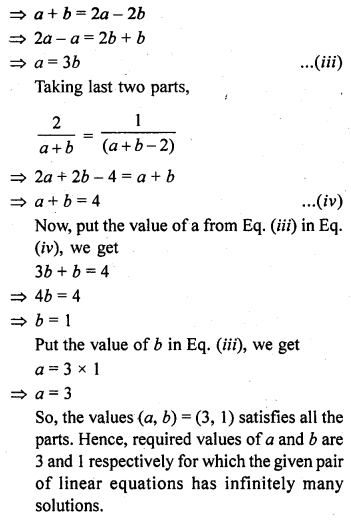
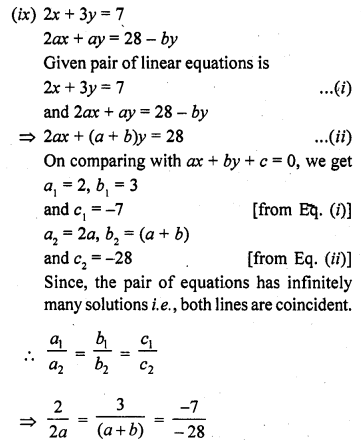
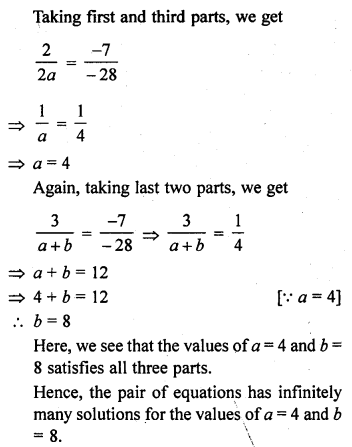
Question 37.
For which value(s) of λ, do the pair of linear equations λx + y = λ2 and x + λy = 1 have
(i) no solution ?
(ii) infinitely many solutions ?
(iii) a unique solutions ? [NCERT Exemplar]
Solution:
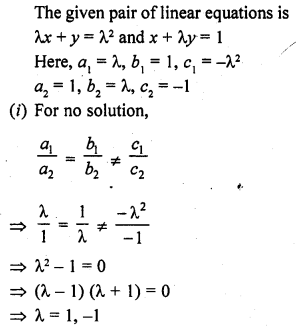
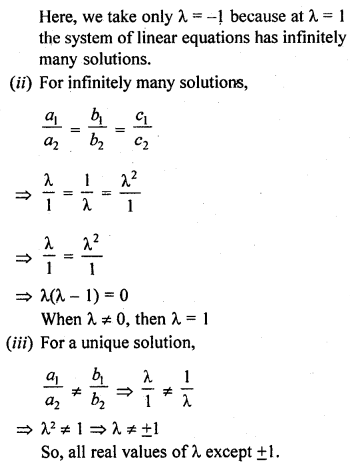
Hope given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.