RD Sharma Class 10 Solutions Chapter 2 Polynomials VSAQS
These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 2 Polynomials VSAQS
Other Exercises
- RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.1
- RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.2
- RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.3
- RD Sharma Class 10 Solutions Chapter 2 Polynomials VSAQS
- RD Sharma Class 10 Solutions Chapter 2 Polynomials MCQS
Answer each of the following questions in one word or one sentence or as per the exact requirement of the questions :
Question 1.
Define a polynomial with real co-efficients.
Solution:
Question 2.
Define degree of a polynomial.
Solution:
The exponent of the highest degree term in a polynomial is known as its degree. A polynomial of degree O is called a constant polynomial.
Question 3.
Write the standard form of a linear polynomial with real co-efficients.
Solution:
ax + b is the standard form of a linear polynomial with real co-efficients and a ≠ 0
Question 4.
Write the standard form of a quadratic polynomial with real co-efficients.
Solution:
ax2 + bx + c is a standard form of quadratic polynomial with real co-efficients and a ≠ 0.
Question 5.
Write the standard form of a cubic polynomial with real co-efficients.
Solution:
ax3 + bx2 + cx + d is a standard form of cubic polynomial with real co-efficients and a ≠ 0.
Question 6.
Define value of a polynomial at a point.
Solution:
If f(x) is a polynomial and a is any real number then the real number obtained by replacing x by α in f(x) is called the value of f(x) at x = α and is denoted by f(α).
Question 7.
Define zero of a polynomial.
Solution:
A real number a is a zero of a polynomial f(x) if f(α) = 0.
Question 8.
The sum and product of the zeros of a quadratic polynomial are – \(\frac { 1 }{ 2 }\) and -3 respectively. What is the quadratic polynomial ?
Solution:
Question 9.
Write the family of quadratic polynomials having – \(\frac { 1 }{ 4 }\) and 1 as its zeros.
Solution:

Question 10.
If the product of zeros of the quadratic polynomial f(x) = x2 – 4x + k is 3, find the value of k.
Solution:
We know that a quadratic polynomial x2 – (sum of zeros) x + product of zeros
In the given polynomial f(x) = x2 – 4x + k is the product of zeros which is equal to 3
k = 3
Question 11.
If the sum of the zeros of a quadratic polynomial f(x) = kx2 – 3x + 5 is 1, write the value of k.
Solution:
f (x) = kx2 – 3x + 5
Here a = k, b = -3, c = 5
Question 12.
In the figure, the graph of a polynomial p (x) is given. Find the zeros of the polynomial.
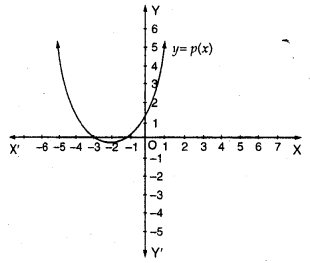
Solution:
The graph of the given polynomial meets the x-axis at -1 and -3
Zero will be -1 and -3
Zero of polynomial is 3
Question 13.
The graph of a polynomial y = f(x) is given below. Find the number of real zeros of f (x).
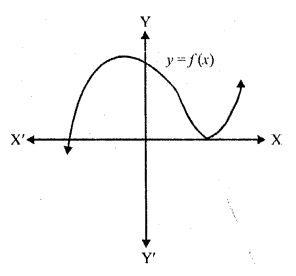
Solution:
The curve touches x-axis at one point and also intersects at one point So number of zeros will be 3, two equal and one distinct
Question 14.
The graph of the polynomial f(x) = ax2 + bx + c is as shown below (in the figure) write the signs of ‘a’ and b2 – 4ac.
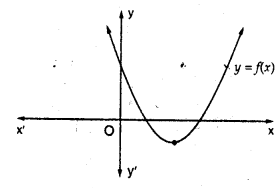
Solution:
The shape of parabola is up word a > 0
and b2 – 4ac >0 i.e., both are positive.
Question 15.
The graph of the polynomial f(x) = ax2 + bx + c is as shown in the figure write the value of b2 – 4ac and the number of real zeros of f(x).
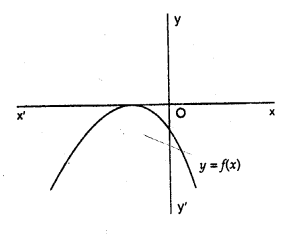
Solution:
The curve parabola touches the x-axis at one point
It has two equal zeros
b2 – 4ac = 0
Question 16.
In Q. No. 14, write the sign of c
Solution:
The mouth of parabola is upward and intersect y-axis above x-axis
c > 0
Question 17.
In Q. No. 15, write the sign of c.
Solution:
The mouth of parabola is downward and intersects y-axis below x-axis
c < 0
Question 18.
The graph of a polynomial f (x) is as shown in the figure. Write the number of real zeros of f (x).
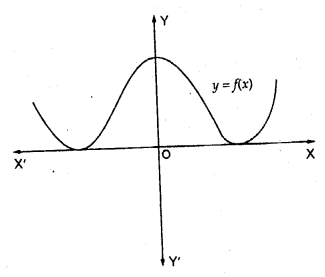
Solution:
The curves touches the x-axis at two distinct point
It has a pair of two equal zeros i.e., it has 4 real zeros
Question 19.
If x = 1, is a zero of the polynomial f(x) = x3 – 2x2 + 4x + k, write the value of k.
Solution:
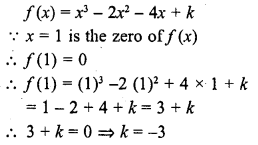
Question 20.
State division algorithm for polynomials.
Solution:
If f(x) is a polynomial and g (x) is a non zero polynomial, there exist two polynomials q (x) and r (x) such that
f(x) = g (x) x q (x) + r (x)
where r (x) = 0 or degree r (x) < degree g (x)
This is called division algorithm
Question 21.
Give an example of polynomials f(x), g (x), q (x) and r (x) satisfying f(x) = g (x) . q (x) + r (x), where degree r (x) = 0.
Solution:
f (x) = x3 + x2 + x + 4
g (x) = x + 1
q (x) = x2 + 1
r (x) = 3
is an example of f (x) = g (x) x q (x) + r (x)
where degree of r (x) is zero.
Question 22.
Write a quadratic polynomial, sum of whose zeros is 2√3 and their product is 2.
Solution:
Sum of zeros = 2 √3
and product of zeros = 2
Quadratic polynomial will be f (x) = x2 – (sum of zeros) x + product of zeros
= x2 – 2 √3 x + 2
Question 23.
If fourth degree polynomial is divided by a quadratic polynomial, write the degree of the remainder.
Solution:
Degree of the given polynomial = 4
and degree of divisor = 2
Degree of quotient will be 4 – 2 = 2
and degree of remainder will be less than 2 In other words equal to or less than one degree
Question 24.
If f(x) = x3 + x2 – ax + b is divisible by x2 – x, write the value of a and b.
Solution:
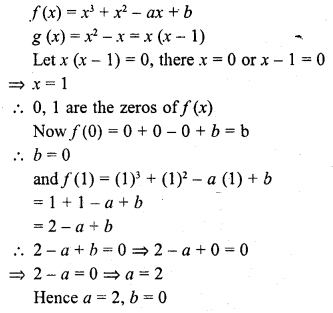
Question 25.
If a – b, a and a + b are zeros of the polynomial f(x) = 2x3 – 6x2 + 5x – 7, write the value of a.
Solution:
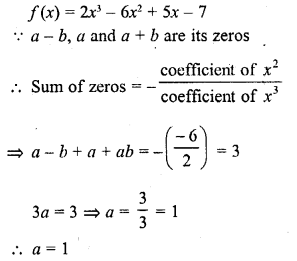
Question 26.
Write the coefficients of the polynomial p (z) = z5 – 2z2 + 4.
Solution:
p (z) = z5 + oz4 + oz3 – 2z2 + oz + 4
Coefficient of z5 = 1
Coefficient of z4 = 0
Coefficient of z3 = 0
Coefficient of z2 = – 2
Coefficient of z = 0
Constant = 4
Question 27.
Write the zeros of the polynomial x2 – x – 6. (C.B.S.E. 2008)
Solution:
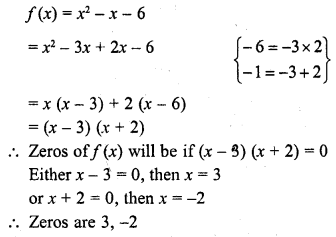
Question 28.
If (x + a) is a factor of 2x2 + 2ax + 5x + 10, find a. (C.B.S.E. 2008)
Solution:
x + a is a factor of
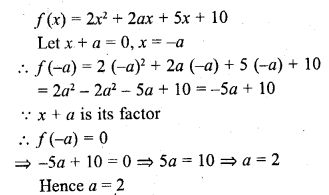
Question 29.
For what value of k, -4 is a zero of the polynomial x2 – x – (2k + 2) ? (CBSE 2009)
Solution:
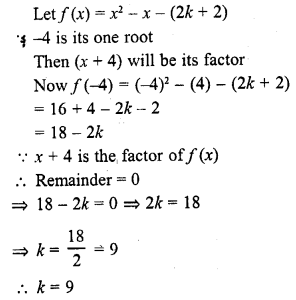
Question 30.
If 1 is a zero of the polynomial p (x) = ax2 – 3 (a – 1) x – 1, then find the value of a.
Solution:
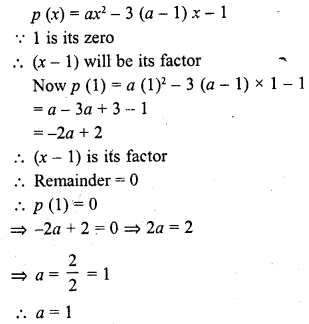
Question 31.
If α, β are the zeros of a polynomial such that α + β = -6 and α β = -4, then write the polynomial. [CBSE 2010]
Solution:
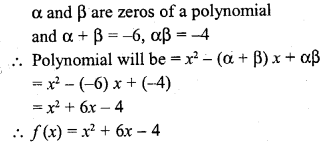
Question 32.
If α, β are the zeros of the polynomial 2y2 + 7y + 5, write the value of α + β + αβ. [CBSE 2010]
Solution:
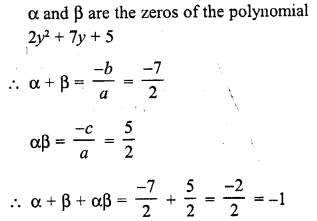
Question 33.
For what value of k, is 3 a zero of the polynomial 2x2 + x + k ? [CBSE 2010]
Solution:
3 is a zero of f(x) = 2x2 + x + k
It will satisfy the polynomial
f(x) = 0 ⇒ f(3) = 0
Now 2x2 + x + k = 0
=> 2 (3)2 + 3 + k = 0
=> 18 + 3 + k = 0
=> 21 + k = 0
=> k = -21
Question 34.
For what value of k, is -3 a zero of the polynomial x2 + 11x + k ? [CBSE 2010]
Solution:
-3 is a zero of polynomial f(x) = x2 + 11x + k
It will satisfy the polynomial
f (x) = 0 => f(-3) = 0
Now x2 + 11x + k = 0
=> (-3)2+ 11 x (-3) + k = 0
⇒ 9 – 33 + k = 0
⇒ -24 + k = 0
⇒ k = 24
Question 35.
For what value of k, is -2 a zero of the polynomial 3x2 + 4x + 2k ? [CBSE 2010]
Solution:
-2 is a zero of the polynomial
f(x) = 3x2 + 4x + 2k
f(-2) = 0
=> 3 (-2)2 + 4 (-2) + 2k = 0
=> 12 – 8 + 2k = 0
=> 4 + 2k = 0
=> 2k = -4
=> k = -2
Question 36.
If a quadratic polynomial f(x) is factorizable into linear distinct factors, then what is the total number of real and distinct zeros of f (x) ?
Solution:
In a quadratic polynomial f(x) its degree is 2 and it can be factorised in to two distinct linear factors.
f(x) has two distinct zeros
Question 37.
If a quadratic polynomiaI f(x) is a square of a linear polynomial, then its two zeros are coincident. (True / False)
Solution:
In a quadratic polynomial f(x), it is the square of a linear polynomial It has two zeros which are equal i.e. coincident
It is true
Question 38.
If a quadratic polynomial f(x) is not factorizable into linear factors, then it has no real zero. (True / False)
Solution:
A quadratic polynomial f(x) is not factorised into linear factors It has no real zeros It is true
Question 39.
If f(x) is a polynomial such that f(a) f(b) < 0, then what is the number of zeros lying between a and b ?
Solution:
f(x) is a polynomial such that f(a) f(b) < 0
At least one of its zeros will be between a and b
Question 40.
If graph of quadratic polynomial ax2 + bx + c cuts positive direction of y-axis, then what is the sign of c ?
Solution:
The graph of quadratic polynomial ax2 + bx + c cuts positive direction of y-axis Then sign of constant term c will be also positive.
Question 41.
If the graph of quadratic polynomial ax2 + bx + c cuts negative direction of y-axis, then what is the sigh of c ?
Solution:
The graph of quadratic polynomial ax2 + bx + c cuts negative side of y-axis
Then sign of constant term c will be negative
Hope given RD Sharma Class 10 Solutions Chapter 2 Polynomials VSAQS are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.