RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.1
These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.1
Other Exercises
- RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.1
- RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.2
- RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.3
- RD Sharma Class 10 Solutions Chapter 2 Polynomials VSAQS
- RD Sharma Class 10 Solutions Chapter 2 Polynomials MCQS
Question 1.
Find the zeros of each of the following quadratic polynomials and verify the relationship between the zeros and their co-efficients :
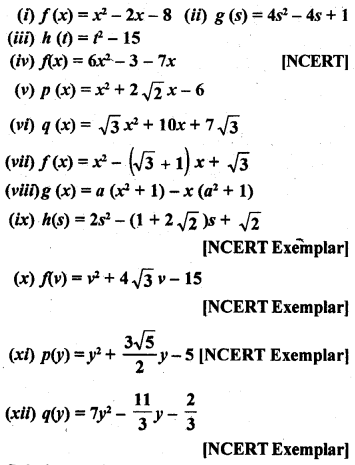
Solution:
(i) f(x) = x2 – 2x – 8

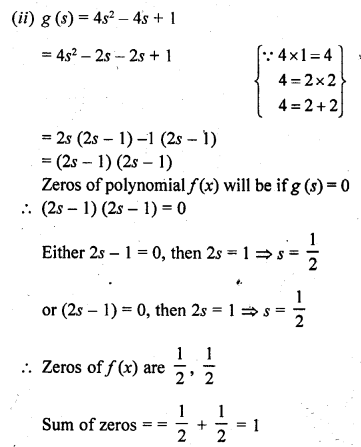


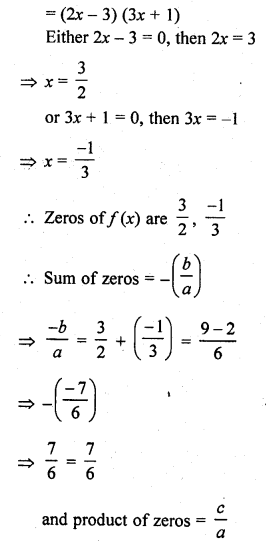
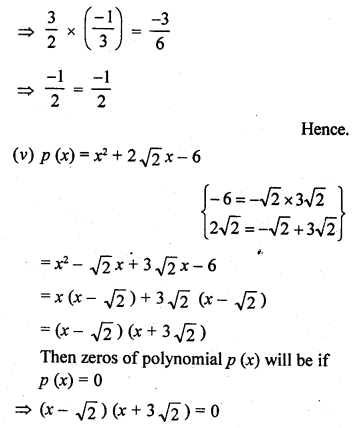

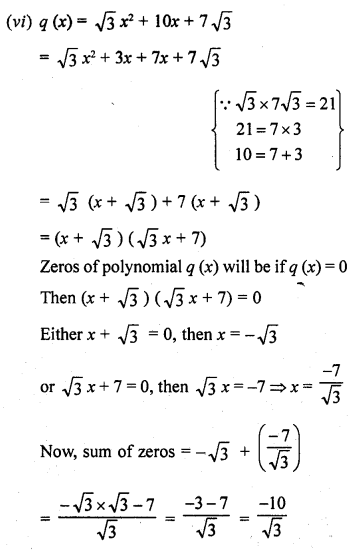


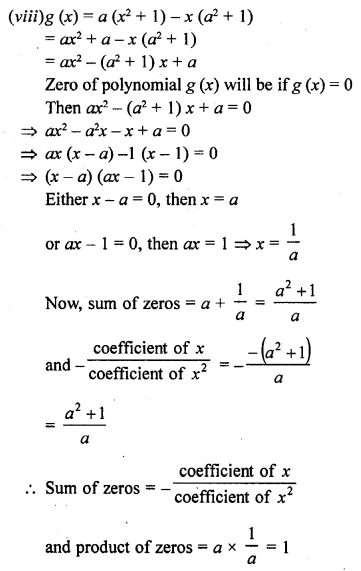


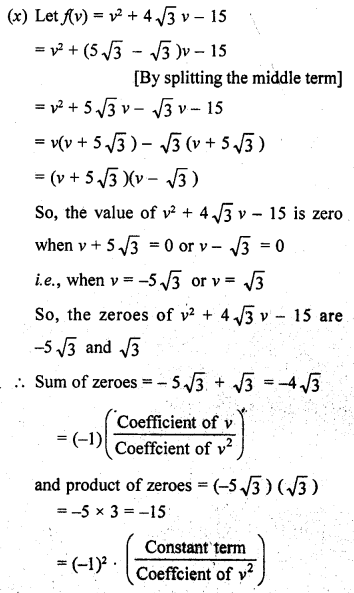
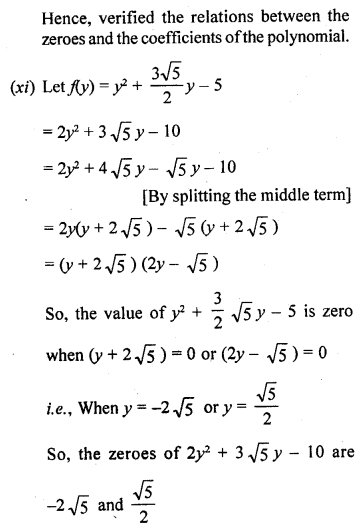

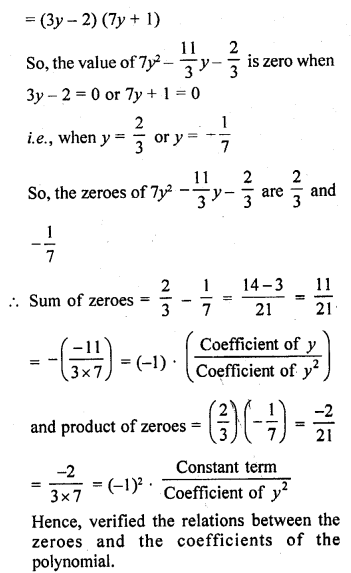
Question 2.
For each of the following, find a quadratic polynomial whose sum and product respectively of the zeroes are as given. Also, find the zeroes of these polynomials by factorization.
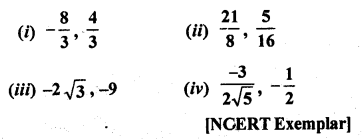
Solution:
(i) Given that, sum of zeroes (S) = – \(\frac { 8 }{ 3 }\)
and product of zeroes (P) = \(\frac { 4 }{ 3 }\)
Required quadratic expression,

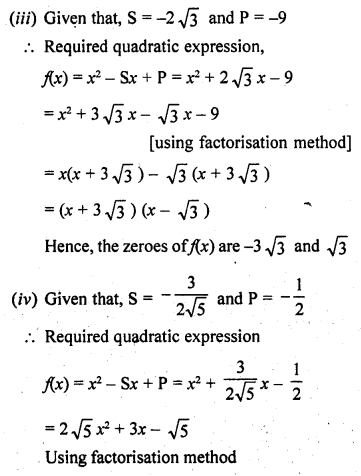
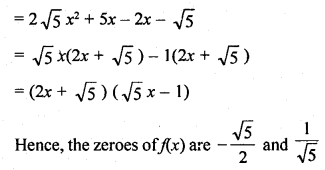
Question 3.
If α and β are the zeros of the quadratic polynomial f(x) = x2 – 5x + 4, find the value of \(\frac { 1 }{ \alpha } +\frac { 1 }{ \beta } -2\alpha \beta\).
Solution:
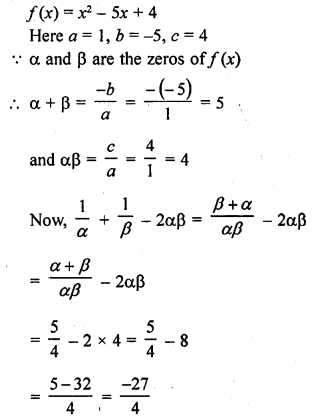
Question 4.
If α and β are the zeros of the quadratic polynomial p(y) = 5y2 – 7y + 1, find the value of \(\frac { 1 }{ \alpha } +\frac { 1 }{ \beta }\)
Solution:
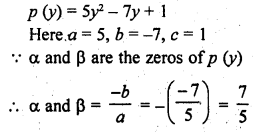
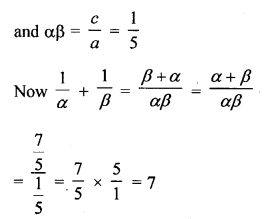
Question 5.
If α and β are the zeros of the quadratic polynomial f(x) = x2 – x – 4, find the value of \(\frac { 1 }{ \alpha } +\frac { 1 }{ \beta } -\alpha \beta\)
Solution:
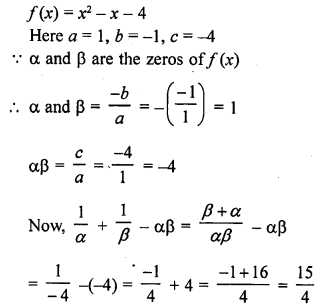
Question 6.
If α and β are the zeros of the quadratic polynomial f(x) = x2 + x – 2, find the value of \(\frac { 1 }{ \alpha } -\frac { 1 }{ \beta }\)
Solution:
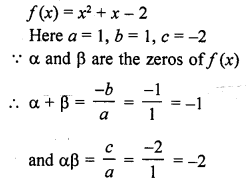
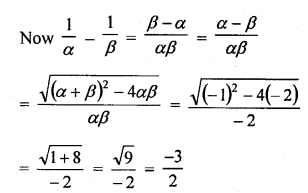
Question 7.
If one zero of the quadratic polynomial f(x) = 4x2 – 8kx – 9 is negative of the other, find the value of k.
Solution:
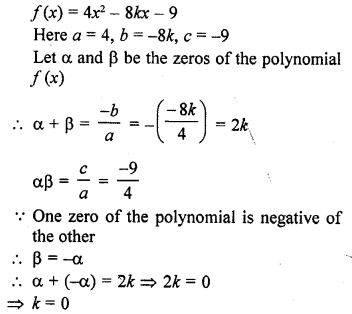
Question 8.
If the sum of the zeros of the quadratic polynomial f(t) = kt2 + 2t + 3k is equal to their product, find the value of k.
Solution:
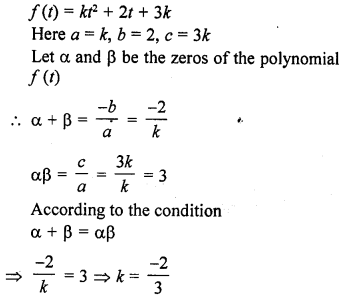
Question 9.
If α and β are the zeros of the quadratic polynomial p(x) = 4x2 – 5x – 1, find the value of α2β + αβ2.
Solution:
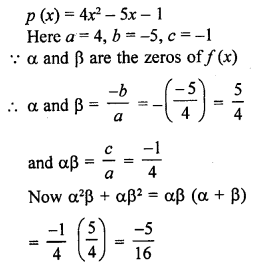
Question 10.
If α and β are the zeros of the quadratic polynomial f(t) = t2 – 4t + 3, find the value of α4β3 + α3β4.
Solution:
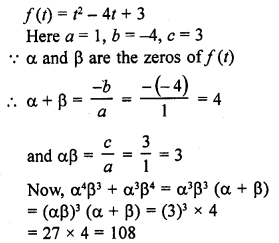
Question 11.
If α and β are the zeros of the quadratic polynomial f (x) = 6x4 + x – 2, find the value of \(\frac { \alpha }{ \beta } +\frac { \beta }{ \alpha }\)
Solution:
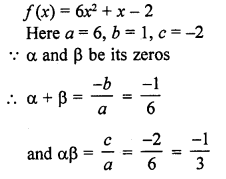
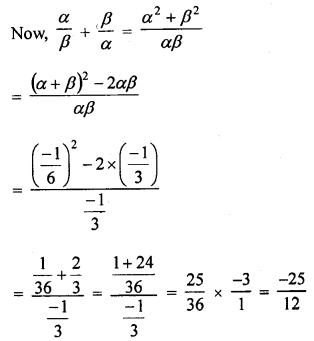
Question 12.
If α and β are the zeros of the quadratic polynomial p(s) = 3s2 – 6s + 4, find the value of \(\frac { \alpha }{ \beta } +\frac { \beta }{ \alpha } +2\left( \frac { 1 }{ \alpha } +\frac { 1 }{ \beta } \right) +3\alpha \beta\)
Solution:
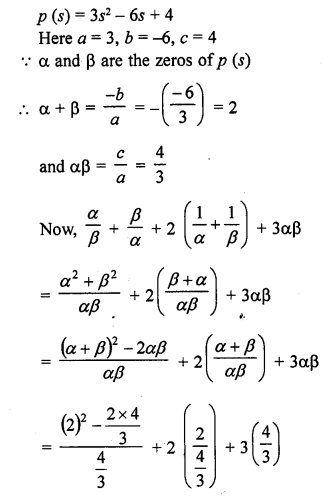
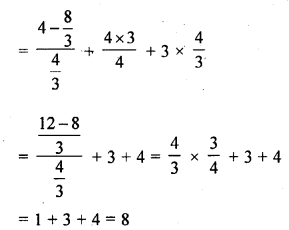
Question 13.
If the squared difference of the zeros of the quadratic polynomial f(x) = x2 + px + 45 is equal to 144, find the value of p
Solution:
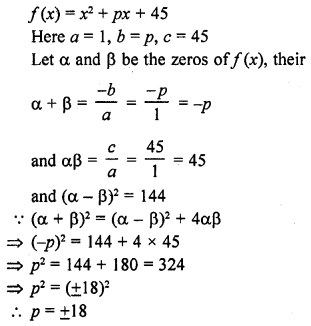
Question 14.
If α and β are the zeros of the quadratic polynomial f(x) = x2 – px + q, prove that:
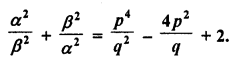
Solution:
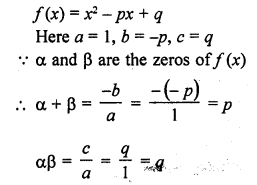
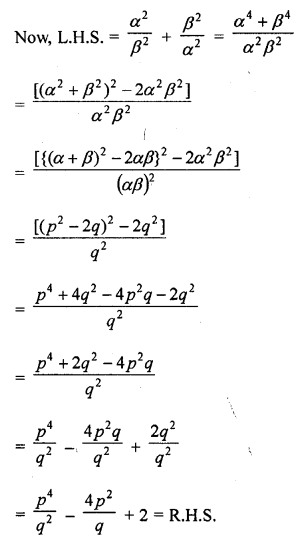
Question 15.
If α and β are the zeros of the quadratic polynomial f(x) = x2 – p(x + 1) – c, show that (α + 1) (β + 1) = 1 – c.
Solution:
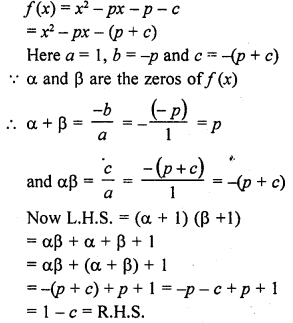
Question 16.
If α and β are the zeros of the quadratic polynomial such that α + β = 24 and α – β = 8, find a quadratic polynomial having α and β as its zeros.
Solution:
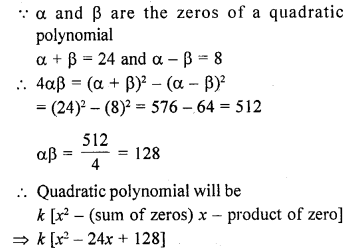
Question 17.
If α and β are the zeros of the quadratic polynomial f(x) = x2 – 1, find a quadratic polynomial whose zeros are \(\frac { 2\alpha }{ \beta }\) and \(\frac { 2\beta }{ \alpha }\)
Solution:
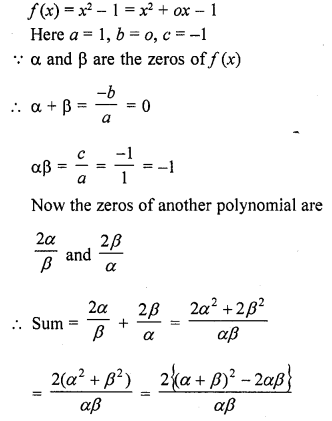
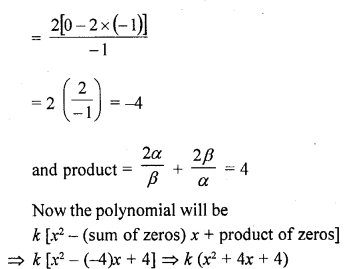
Question 18.
If α and β are the zeros of the quadratic polynomial f(x) = x2 – 3x – 2, find a quadratic polynomial whose zeros are \(\frac { 1 }{ 2\alpha +\beta }\) and \(\frac { 1 }{ 2\beta +\alpha }\)
Solution:
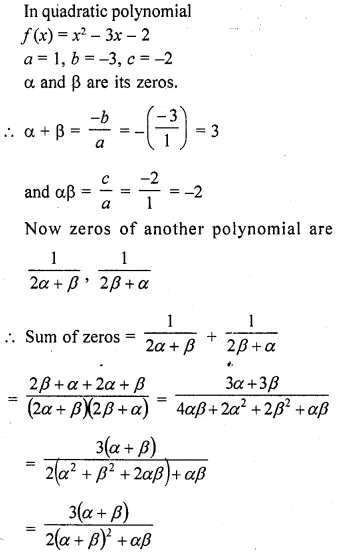
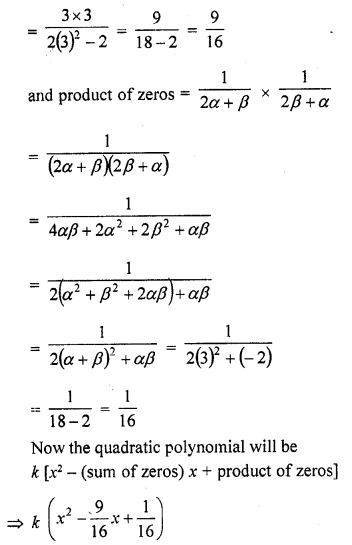
Question 19.
If α and β are the zeroes of the polynomial f(x) = x2 + px + q, form a polynomial whose zeros are (α + β)2 and (α – β)2.
Solution:
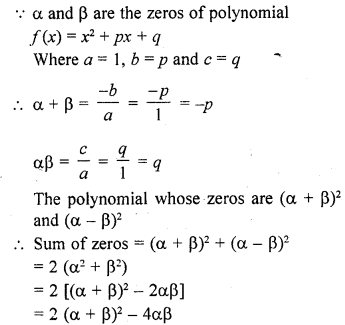
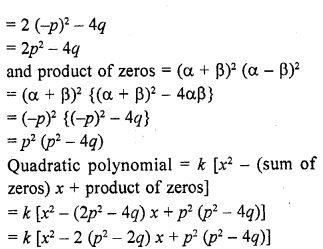
Question 20.
If α and β are the zeros of the quadratic polynomial f(x) = x2 – 2x + 3, find a polynomial whose roots are :
(i) α + 2, β + 2
(ii) \(\frac { \alpha -1 }{ \alpha +1 } ,\frac { \beta -1 }{ \beta +1 }\)
Solution:
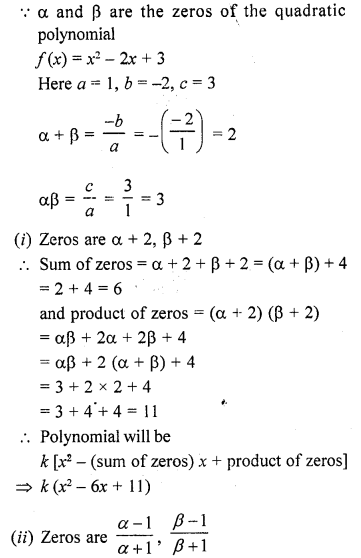
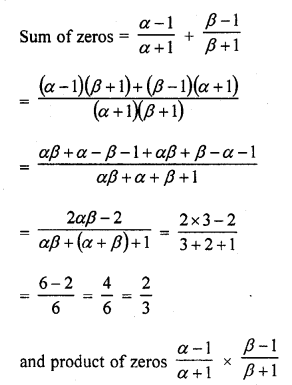
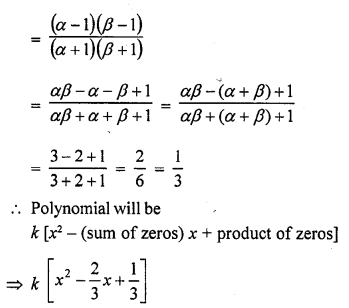
Question 21.
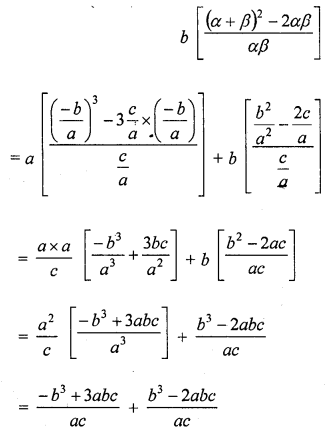
If α and β are the zeros of the quadratic polynomial f(x) = ax2 + bx + c, then evaluate :
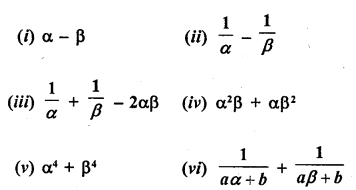
Solution:
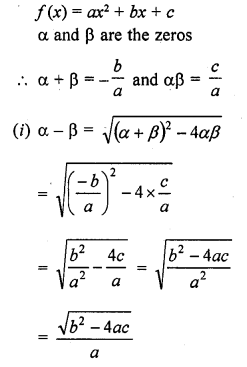
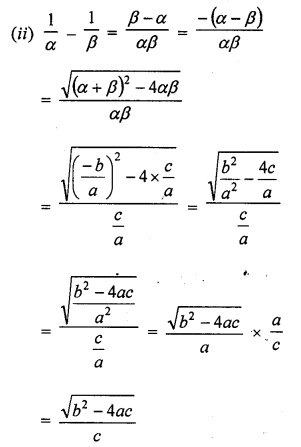
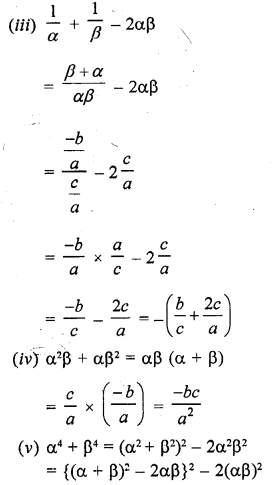
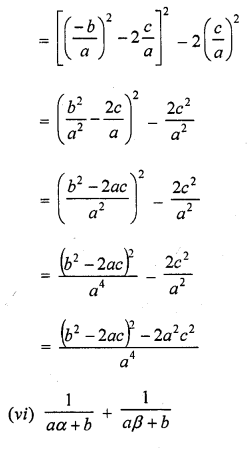
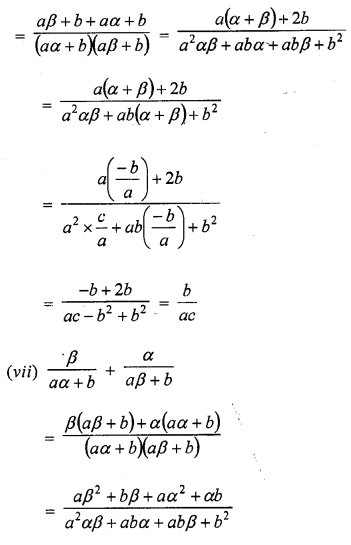
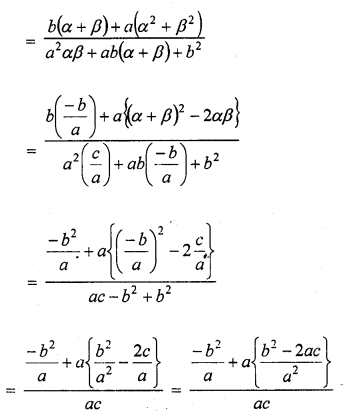
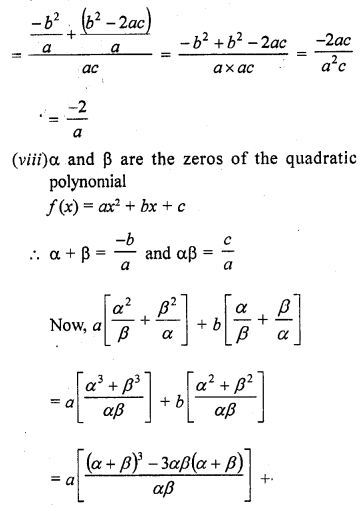
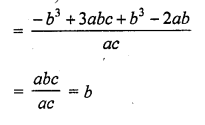
Hope given RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.1 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.