RD Sharma Class 10 Solutions Chapter 2 Polynomials MCQS
These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 2 Polynomials MCQS. You must go through NCERT Solutions for Class 10 Maths to get better score in CBSE Board exams along with RS Aggarwal Class 10 Solutions.
Mark the correct alternative in each of the following :
Question 1.
If α, β are the zeros of the polynomial f(x) = x2 + x + 1, then \(\frac { 1 }{ \alpha } +\frac { 1 }{ \beta }\) =
(a) 1
(b) -1
(c) 0
(d) None of these
Solution:
(b)
Polynomial Root calculator. Welcome to our step-by-step math solver! Solve · Simplify · Factor
Question 2.
If α, β are the zeros of the polynomial p(x) = 4x2 + 3x + 7, then \(\frac { 1 }{ \alpha } +\frac { 1 }{ \beta }\) is equal to
(a) \(\frac { 7 }{ 3 }\)
(b) – \(\frac { 7 }{ 3 }\)
(c) \(\frac { 3 }{ 7 }\)
(d) – \(\frac { 3 }{ 7 }\)
Solution:
(d)
Question 3.
If one zero of the polynomial f(x) = (k2 + 4) x2 + 13x + 4k is reciprocal of the other, then k =
(a) 2
(b) -2
(c) 1
(d) -1
Solution:
(a) f (x) = (k2 + 4) x2 + 13x + 4k
Here a = k2 + 4, b = 13, c = 4k
One zero is reciprocal of the other
Let first zero = α
k = 2
Question 4.
If the sum of the zeros of the polynomial f(x) = 2x3 – 3kx2 + 4x – 5 is 6, then value of k is
(a) 2
(b) 4
(c) -2
(d) -4
Solution:
(b)
Question 5.
If α and β are the zeros of the polynomial f(x) = x2 + px + q, then a polynomial having α and β is its zeros is
(a) x2 + qx + p
(b) x2 – px + q
(c) qx2 + px + 1
(d) px2 + qx + 1
Solution:
(c)
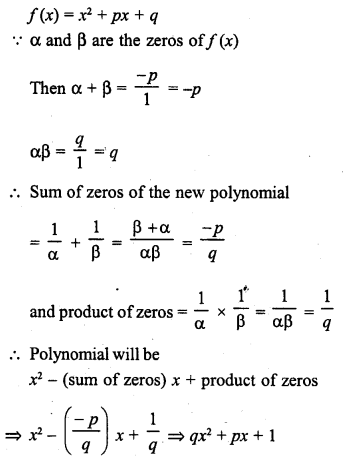
Question 6.
If α, β are the zeros of polynomial f(x) = x2 – p (x + 1) – c, then (α + 1) (β + 1) =
(a) c – 1
(b) 1 – c
(c) c
(d) 1 + c
Solution:
(b)
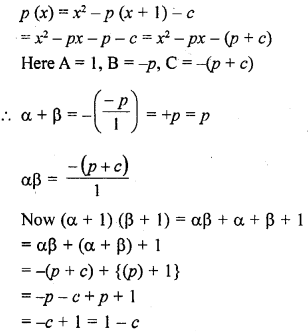
Question 7.
If α, β are the zeros of the polynomial f(x) = x2 – p(x + 1) – c such that (α + 1) (β + 1) = 0, then c =
(a) 1
(b) 0
(c) -1
(d) 2
Solution:
(a)
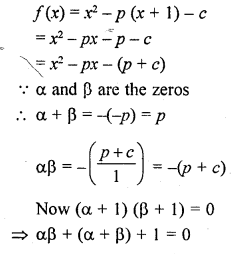
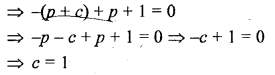
Question 8.
If f(x) = ax2 + bx + c has no real zeros and a + b + c < 0, then
(a) c = 0
(b) c > 0
(c) c < 0
(d) None of these
Solution:
(d) f(x) = ax2 + bx + c
Zeros are not real
b2 – 4ac < 0 ….(i)
but a + b + c < 0
b < – (a + c)
Squaring both sides b2 < (a + c)2
=> (a + c)2 – 4ac < 0 {From (i)}
=> (a – c)2 < 0
=> a – c < 0
=> a < c
Question 9.
If the diagram in figure shows the graph of the polynomial f(x) = ax2 + bx + c, then
(a) a > 0, b < 0 and c > 0
(b) a < 0, b < 0 and c < 0
(c) a < 0, b > 0 and c > 0
(d) a < 0, b > 0 and c < 0
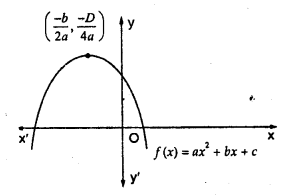
Solution:
(a) Curve ax2 + bx + c intersects x-axis at two points and curve is upward.
a > 0, b < 0 and c> 0
Question 10.
Figure shows the graph of the polynomial f(x) = ax2 + bx + c for which
(a) a < 0, b > 0 and c > 0
(b) a < 0, b < 0 and c > 0
(c) a < 0, b < 0 and c < 0
(d) a > 0, b > 0 and c < 0
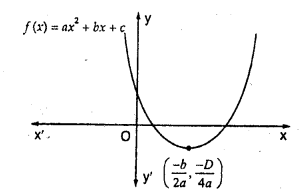
Solution:
(b) Curve ax2 + bx + c intersects x-axis at two points and curve is downward.
a < 0, b < 0 and c > 0
Question 11.
If the product of zeros of the polynomial f(x) = ax3 – 6x2 + 11x – 6 is 4, then a =
(a) \(\frac { 3 }{ 2 }\)
(b) – \(\frac { 3 }{ 2 }\)
(c) \(\frac { 2 }{ 3 }\)
(d) – \(\frac { 2 }{ 3 }\)
Solution:
(a) f(x) = ax3 – 6x2 + 11x – 6
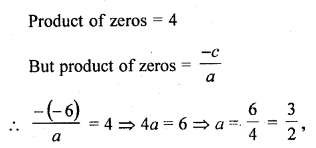
Question 12.
If zeros of the polynomial f(x) = x3 – 3px2 + qx – r are in AP, then
(a) 2p3 = pq – r
(b) 2p3 = pq + r
(c) p3 = pq – r
(d) None of these
Solution:
(a) f(x) = x3 – 3px2 + qx – r
Here a = 1, b = -3p, c = q, d= -r
Zeros are in AP
Let the zeros be α – d, α, α + d
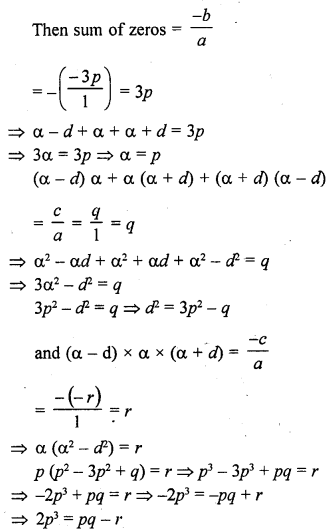
Question 13.
If the product of two zeros of the polynomial f(x) = 2x3 + 6x2 – 4x + 9 is 3, then its third zero is
(a) \(\frac { 3 }{ 2 }\)
(b) – \(\frac { 3 }{ 2 }\)
(c) \(\frac { 9 }{ 2 }\)
(d) – \(\frac { 9 }{ 2 }\)
Solution:
(b)
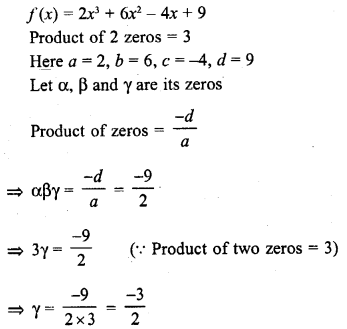
Question 14.
If the polynomial f(x) = ax2 + bx – c is divisible by the polynomial g(x) = ax2 + bx + c, then ab =
(a) 1
(b) \(\frac { 1 }{ c }\)
(c) – 1
(d) – \(\frac { 1 }{ c }\)
Solution:
(a)
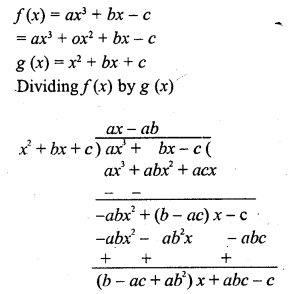
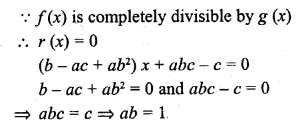
Question 15.
In Q. No. 14, ac =
(a) b
(b) 2b
(c) 2b2
(d) -2b
Solution:
(b) In the previous questions
Remainder = 0
(b – ac + ab2) = 0
b + ab2 = ac
=> ac = b (1 + ab) = b (1 + 1) = 2b
Question 16.
If one root of the polynomial f(x) = 5x2 + 13x + k is reciprocal of the other, then the value of k is
(a) 0
(b) 5
(c) \(\frac { 1 }{ 6 }\)
(d) 6
Solution:
(b)

Question 17.
If α, β, γ are the zeros of the polynomial f(x) = ax3 + bx2 + cx + d, then \(\frac { 1 }{ \alpha } +\frac { 1 }{ \beta } +\frac { 1 }{ \gamma }\) =
(a) – \(\frac { b }{ d }\)
(b) \(\frac { c }{ d }\)
(c) – \(\frac { c }{ d }\)
(d) \(\frac { c }{ a }\)
Solution:
(c)
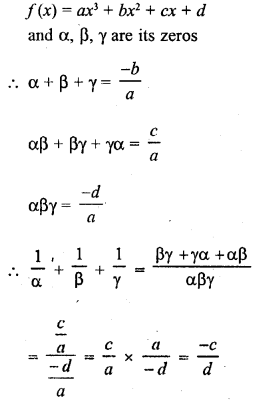
Question 18.
If α, β, γ are the zeros of the polynomial f(x) = ax3 + bx2 + cx + d, then α2 + β2 + γ2 =
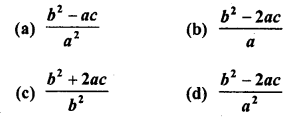
Solution:
(d)
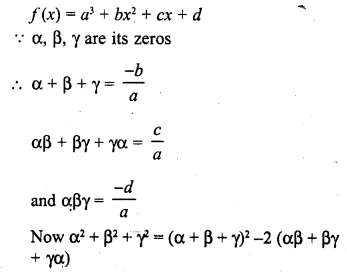
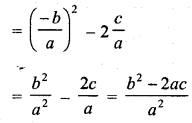
Question 19.
If α, β, γ are the zeros of the polynomial f(x) = x3 – px2 + qx – r, then \(\frac { 1 }{ \alpha \beta } +\frac { 1 }{ \beta \gamma } +\frac { 1 }{ \gamma \alpha }\) =
(a) \(\frac { r }{ p }\)
(b) \(\frac { p }{ r }\)
(c) – \(\frac { p }{ r }\)
(d) – \(\frac { r }{ p }\)
Solution:
(b)
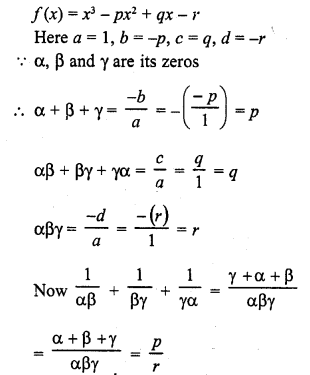
Question 20.
If α, β are the zeros of the polynomial f(x) = ax2 + bx + c, then \(\frac { 1 }{ { \alpha }^{ 2 } } +\frac { 1 }{ { \beta }^{ 2 } }\) =


Solution:
(b)
Question 21.
If two of the zeros of the cubic polynomial ax3 + bx2 + cx + d are each equal to zero, then the third zero is
(a) \(\frac { -d }{ a }\)
(b) \(\frac { c }{ a }\)
(c) \(\frac { -b }{ a }\)
(d) \(\frac { b }{ a }\)
Solution:
(c) Two of the zeros of the cubic polynomial ax3 + bx2 + cx + d are each equal to zero
Let α, β and γ are its zeros, then
Third zero will be \(\frac { -b }{ a }\)
Question 22.
If two zeros of x3 + x2 – 5x – 5 are √5 and – √5 then its third zero is
(a) 1
(b) -1
(c) 2
(d) -2
Solution:
(b)
Question 23.
The product of the zeros of x3 + 4x2 + x – 6 is
(a) – 4
(b) 4
(c) 6
(d) – 6
Solution:
(c)
Question 24.
What should be added to the polynomial x2 – 5x + 4, so that 3 is the zero of the resulting polynomial ?
(a) 1
(b) 2
(c) 4
(d) 5
Solution:
(b) 3 is the zero of the polynomial f(x) = x2 – 5x + 4
x – 3 is a factor of f(x)
Now f(3) = (3)2 – 5 x 3 + 4 = 9 – 15 + 4 = 13 – 15 = -2
-2 is to be subtracting or 2 is added
Question 25.
What should be subtracted to the polynomial x2 – 16x + 30, so that 15 is the zero of the resulting polynomial ?
(a) 30
(b) 14
(b) 15
(d) 16
Solution:
(c) 15 is the zero of polynomial f(x) = x2 – 16x + 30
Then f(15) = 0
f(15) = (15)2 – 16 x 15 + 30 = 225 – 240 + 30 = 255 – 240 = 15
15 is to be subtracted
Question 26.
A quadratic polynomial, the sum of whose zeroes is 0 and one zero is 3, is
(a) x2 – 9
(b) x2 + 9
(c) x2 + 3
(d) x2 – 3
Solution:
(a) In a quadratic polynomial
Let α and β be its zeros
and α + β = 0
and one zero = 3
3 + β = 0 ⇒ β = -3 .
Second zero = -3
Quadratic polynomial will be
(x – 3) (x + 3) ⇒ x2 – 9
Question 27.
If two zeroes of the polynomial x3 + x2 – 9x – 9 are 3 and -3, then its third zero is
(a) -1
(b) 1
(c) -9
(d) 9
Solution:
(a)
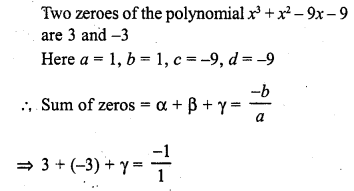
=> γ = -1
Third zero = -1
Question 28.
If √5 and – √5 are two zeroes of the polynomial x3 + 3x2 – 5x – 15, then its third zero is
(a) 3
(b) – 3
(c) 5
(d) – 5
Solution:
(b)
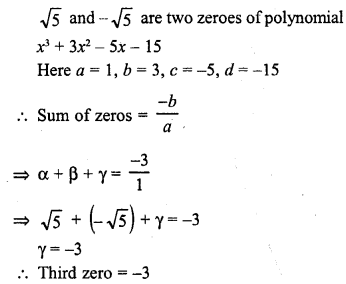
Question 29.
If x + 2 is a factor x2 + ax + 2b and a + b = 4, then
(a) a = 1, b = 3
(b) a = 3, b = 1
(c) a = -1, b = 5
(d) a = 5, b = -1
Solution:
(b) x + 2 is a factor of x2 + ax + 2b and a + b = 4
x + 2 is one of the factor
x = – 2 is its one zero
f(-2) = 0
=> (-2)2 + a (-2) + 2b = 0
=> 4 – 2a + 2b = 0
=> 2a – 2b = 4
=> a – b = 2
But a + b = 4
Adding we get, 2a = 6 => a = 3
and a + b = 4 => 3 + b = 4 => b = 4 – 3 = 1
a = 3, b = 1
Question 30.
The polynomial which when divided by – x2 + x – 1 gives a quotient x – 2 and remainder 3, is
(a) x3 – 3x2 + 3x – 5
(b) – x3 – 3x2 – 3x – 5
(c) – x3 + 3x2 – 3x + 5
(d) x3 – 3x2 – 3x + 5
Solution:
(c) Divisor = – x2 + x – 1, Quotient = x – 2 and
Remainder = 3, Therefore
Polynomial = Divisor x Quotient+Remainder
= (-x2 + x – 1) (x – 2) + 3
= – x3 + x2 – x + 2x2 – 2x + 2 + 3
= – x3 + 3x2 – 3x + 5
Question 31.
The number of polynomials having zeroes -2 and 5 is
(a) 1
(b) 2
(c) 3
(d) more than 3
Solution:
(d)
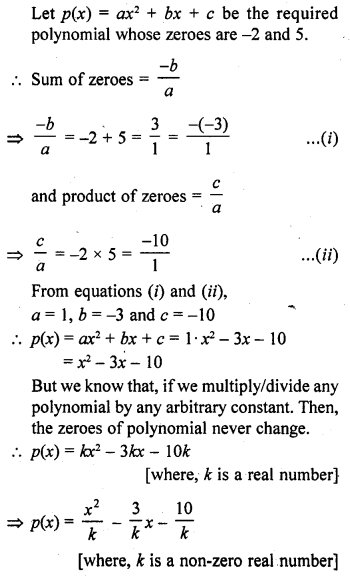
Hence, the required number of polynomials are infinite i.e., more than 3.
Question 32.
If one of the zeroes of the quadratic polynomial (k – 1)x2 + kx + 1 is -3, then the value of k is
(a) \(\frac { 4 }{ 3 }\)
(b) – \(\frac { 4 }{ 3 }\)
(c) \(\frac { 2 }{ 3 }\)
(d) – \(\frac { 2 }{ 3 }\)
Solution:
(a)
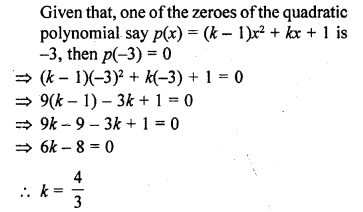
Question 33.
The zeroes of the quadratic polynomial x2 + 99x + 127 are
(a) both positive
(b) both negative
(c) both equal
(d) one positive and one negative
Solution:
(b)

Question 34.
If the zeroes of the quadratic polynomial x2 + (a + 1) x + b are 2 and -3, then
(a) a = -7, b = -1
(b) a = 5, b = -1
(c) a = 2, b = -6
(d) a = 0, b = -6
Solution:
(d)

Question 35.
Given that one of the zeroes of the cubic polynomial ax3 + bx2 + cx + d is zero, the product of the other two zeroes is
(a) – \(\frac { c }{ a }\)
(b) \(\frac { c }{ a }\)
(c) 0
(d) – \(\frac { b }{ a }\)
Solution:
(b)
Question 36.
The zeroes of the quadratic polynomial x2 + ax + a, a ≠ 0,
(a) cannot both be positive
(b) cannot both be negative
(c) area always unequal
(d) are always equal
Solution:
(a) Let p(x) = x2 + ax + a, a ≠ 0
On comparing p(x) with ax2 + bx + c, we get
a = 1, b = a and c = a

So, both zeroes are negative.
Hence, in any case zeroes of the given quadratic polynomial cannot both the positive.
Question 37.
If one of the zeroes of the cubic polynomial x3 + ax2 + bx + c is -1, then the product of other two zeroes is
(a) b – a + 1
(b) b – a – 1
(c) a – b + 1
(d) a – b – 1
Solution:
(a)

=> α β = -a + b + 1
Hence, the required product of other two roots is (-a + b + 1)
Question 38.
Given that two of the zeroes of the cubic polynomial ax3 + bx2 + cx + d are 0, the third zero is
(a) – \(\frac { b }{ a }\)
(b) \(\frac { b }{ a }\)
(c) \(\frac { c }{ a }\)
(d) – \(\frac { d }{ a }\)
Solution:
(a) Two of the zeroes of the cubic polynomial
ax3 + bx2 + cx + d = 0, 0
Let the third zero be d
Then, use the relation between zeroes and coefficient of polynomial, we have
d + 0 + 0 = – \(\frac { b }{ a }\)
⇒ d = – \(\frac { b }{ a }\)
Question 39.
If one zero of the quadratic polynomial x2 + 3x + k is 2, then the value of k is
(a) 10
(b) -10
(c) 5
(d) -5
Solution:
(b) Let the given quadratic polynomial be P(x) = x2 + 3x + k
It is given that one of its zeros is 2
P(2) = 0
=> (2)2 + 3(2) + k = 0 => 4 + 6 + k = 0
=> k + 10 = 0 => k = -10
Question 40.
If the zeroes of the quadratic polynomial ax2 + bx + c, c ≠ 0 are equal, then
(a) c and a have opposite signs
(b) c and b have opposite signs
(c) c and a have the same sign
(d) c and b have the same sign
Solution:
(c) The zeroes of the given quadratic polynomial ax2 + bx + c, c ≠ 0 are equal. If coefficient of x2 and constant term have the same sign
i.e., c and a have the same sign. While b i.e., coefficient of x can be positive/negative but not zero.

Question 41.
If one of the zeroes of a quadratic polynomial of the form x2 + ax + b is the negative of the other, then it
(a) has no linear term and constant term is negative.
(b) has no linear term and the constant term is positive.
(c) can have a linear term but the constant term is negative.
(d) can have a linear term but the constant term is positive.
Solution:
(a)

Given that, one of the zeroes of a quadratic polynomial p(x) is negative of the other.
αβ < 0
So, b < 0 [from Eq. (i)]
Hence, b should be negative Put a = 0, then,
p(x) = x2 + b = 0 => x2 = – b
=> x = ± √-b [ b < 0]
Hence, if one of the zeroes of quadratic polynomial p(x) is the negative of the other, then it has no linear term i.e., a = 0 and the constant term is negative i.e., b < 0. Alternate Method Let f(x) = x2 + ax + b and by given condition the zeroes are a and -a. Sum of the zeroes = α – α = a => a = 0
f(x) = x2 + b, which cannot be linear and product of zeroes = α (-α) = b
=> – α2 = b
which is possible when, b < 0.
Hence, it has no linear term and the constant tenn is negative.
Question 42.
Which of the following is not the graph of a quadratic polynomial?
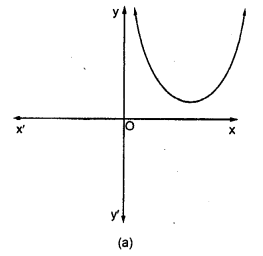
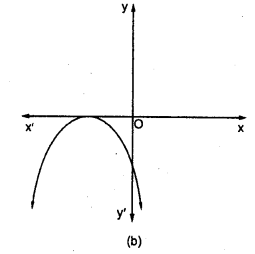
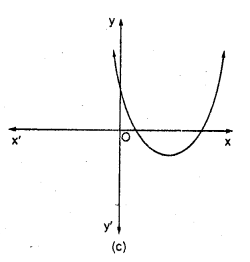
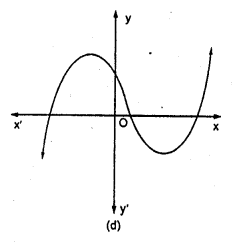
Solution:
(d) For any quadratic polynomial ax2+ bx + c, a 0, the graph of the corresponding equation y = ax2 + bx + c has one of the two shapes either open upwards like ∪ or open downwards like ∩ depending on whether a > 0 or a < 0. These curves are called parabolas. So, option (d) cannot be possible.
Also, the curve of a quadratic polynomial crosses the X-axis on at most two points but in option (d) the curve crosses the X-axis on the three points, so it does not represent the quadratic polynomial.
Hope given RD Sharma Class 10 Solutions Chapter 2 Polynomials MCQS are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.