RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2
These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2
Other Exercises
- RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1
- RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2
- RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3
- RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise
- RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS
- RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS
Question 1.
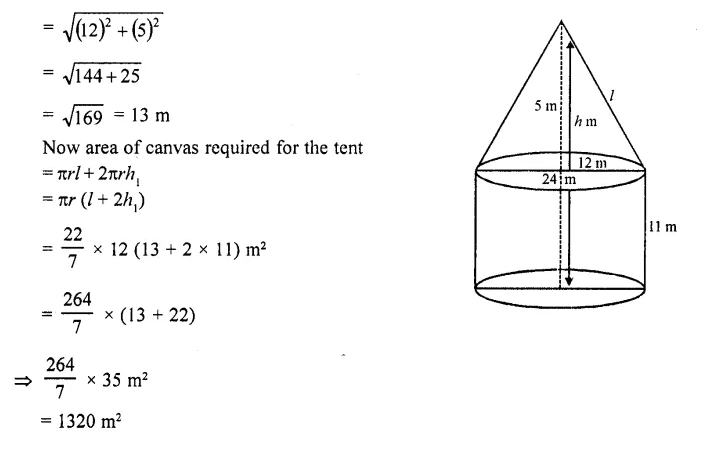
A tent is in the form of a right circular cylinder surmounted by a cone. The diameter of cylinder is 24 m. The height of the cylindrical portion is 11 m while the vertex of the cone is 16 m above the ground. Find the area of canvas required for the tent.
Solution:
Diameter of the base of the tent = 24 m
∴ Radius (r)= \((\frac { 24 }{ 2 } )\) = 12m
Total height of the tent = 16 m
Height of the cylindrical portion (h1) = 11 m
Height of the conical portion (h2) =16-11 = 5 m
Question 2.
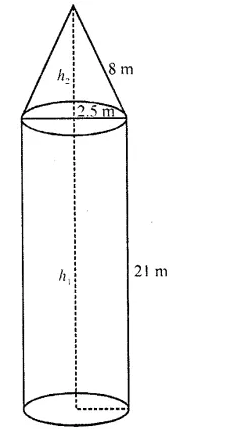
A rocket is in the form of a circular cylinder closed at the lower end with a cone of the same radius attached to the top. The cylinder is of radius 2.5 m and height 21 m and the cone has the slant height 8 m. Calculate the total surface area and the volume of the rocket.
Solution:
Radius of the base of the rocket (r) = 2.5 m
Height of cylindrical portion (h1) = 21 m
Slant height of the conical portion (l) = 8 m
Let height of conical portion = h2

Question 3.
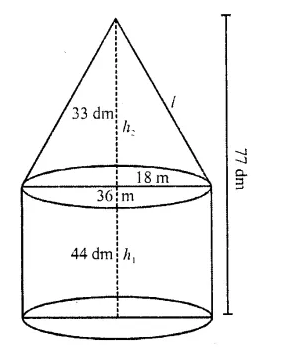
A tent of height 77 dm is in the form of a right circular cylinder of diameter 36 m and height 44
dm surmounted by a right circular cone. Find the cost of the canvas at Rs. 3.50 per m2 . (Use π = 22/7).
Solution:
Total height of the tent = 77 dm
Height of cylindrical part (h1) = 44 dm
= 4.4 m
Height of conical part (h2) = 7.7 – 4.4 = 3.3 m
Diameter of the base of the tent = 36 m

Question 4.
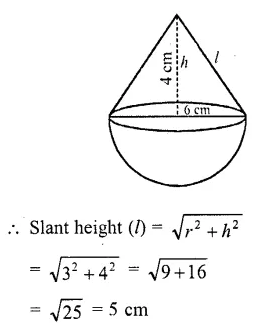
A toy is in the form of a cone surmounted on a hemisphere. The diameter of the base and the height of the cone are 6 cm and 4 cm, respectively. Determine the surface area of the toy. (Use π = 3.14).
Solution:
Diameter of the base of the toy = 6 cm
∴ Radius (r) = \((\frac { 6 }{ 2 } )\) = 3 cm
Height (h) = 4 cm
Total surface area of the toy = curved surface area of the conical part + surface area of the hemispherical part
= πrl + 2πr² = πr (l + 2r)
= 3.14 x 3 (5 + 6) = 3.14 x 3 x 11 cm²
= 3.14 x 33 = 103.62 cm²
Question 5.
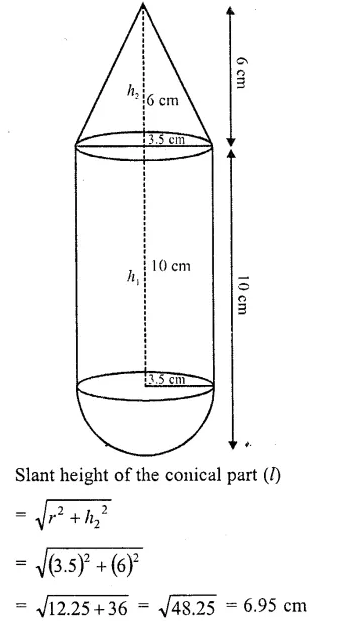
A solid is in the form of a right circular cylinder, with a hemisphere at one end and a cone at the other end. The radius of the common base is 3.5 cm and the ~ heights of the cylindrical and conical portions are 10 cm and 6 cm, respectively. Find the total surface area of the solid. (Use π = 22/7)
Solution:
Radius of the common base (r) = 3.5 m
Height of cylindrical part (h1) = 10 cm
Height of conical part (h2) = 6 cm
Now total surface area of the solid = curved surface of conical part + curved surface of cylindrical part + curved surface of hemispherical part
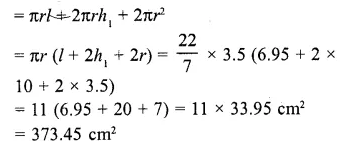
Question 6.
A toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The radius and height of the cylindrical part are 5 cm and 13 cm respectively. The radii of the hemispherical and conical parts are the same as that of the cylindrical part. Find the surface area of the toy if the total height of the toy is 30 cm. (C.B.S.E. 2002)
Solution:
Radius of the base of the cylindrical part (r) = 5 cm
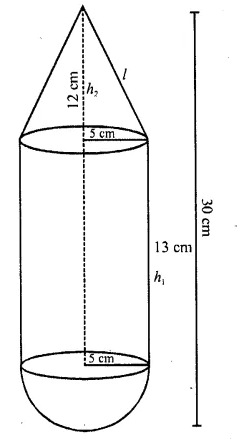
Height of cylindrical part (h1) = 13 cm
Height of the conical part (h2) = 30 – (13 + 5) = 30- 18 = 12 cm
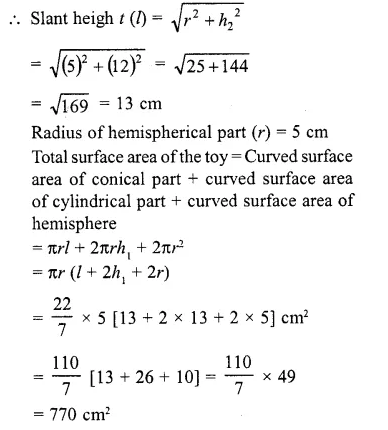
Question 7.
A cylindrical tub of radius 5 cm and length 9.8 cm is full of water. A solid in the form of a right circular cone mounted on a hemisphere is immersed in the tub. If the radius of the hemisphere is immersed in the tub. If the radius of the hemi-sphere is 3.5 cm and height of the cone outside the hemisphere is 5 cm, find the volume of the water left in the tub. (Take π = 22/7) (C.B.S.E. 2000C)
Solution:
Radius of the cylindrical tub (R) = 5 cm
and height (h1) = 9.8 cm
Radius of the solid (r) = 3.5 cm
and height of cone (h1) = 5 cm
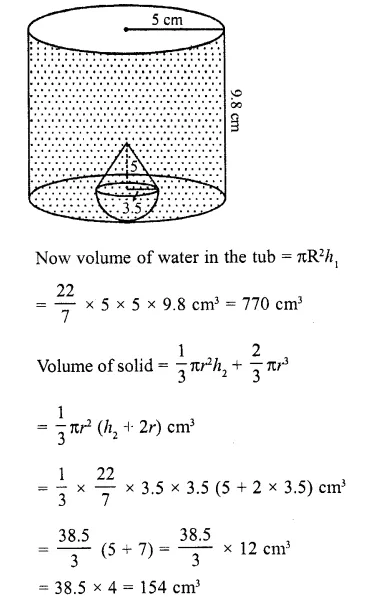
= 38.5 x 4 = 154 cm3
∴ Water flowed out of the tub = 154 cm³
Remaining water in the tub = 770 – 154
= 616 cm³
Question 8.
A circus tent has cylindrical shape surmounted by a conical roof. The radius of the cylindrical base is 20 m. The heights of the cylindrical and conical portions are 4.2 m and 2.1 m respectively. Find the volume of the tent.
Solution:
Radius of the tent (r) = 20 m
Height of the conical part (h1) = 2.1 m
and height of the cylindrical part (h2) = 4.2 m

Question 9.
A petrol tank is a cylinder of base diameter 21 cm and length 18 cm fitted with conical ends each of axis length 9 cm. Determine the capacity of the tank.
Solution:
Diameter of cylindrical part = 21 cm 21
∴ Radius (r) = \((\frac { 21 }{ 2 } )\) cm
Height of cylindrical part (h1) = 18 cm
and height of each conical part (h2) = 9 cm
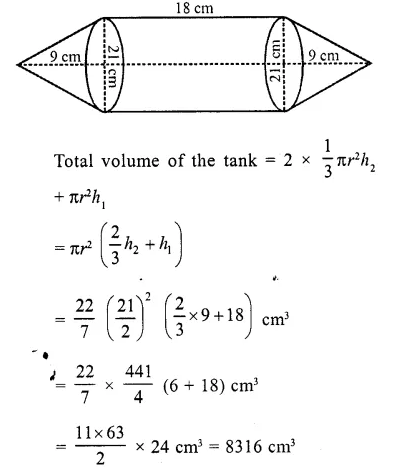
Question 10.
A conical hole is drilled in a circular cylinder of height 12 cm and base radius 5 cm. The height and the base radius of the cone are also the same. Find the whole surface and volume of the remaining cylinder.
Solution:
Base radius of the cylinder (r) = 5 cm
and height (h) = 12 cm
∴ Volume = πr2h = n (5)2 x 12 cm3 = 300π cm3
∵ The base and height of the cone drilled are the same as those of the cylinder
∴ Volume of cone = \((\frac { 1 }{ 3 } )\)πr2h
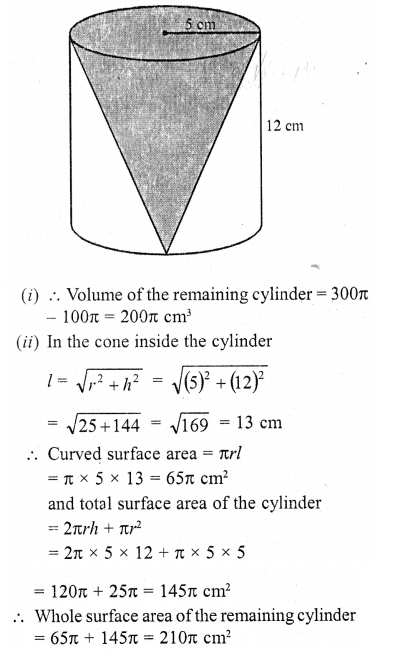
Question 11.
A tent is in the form of a cylinder of diameter 20 m and height 2.5 m, surmounted by a cone of equal base and height 7.5 m. Find the capacity of the tent and the cost of the canvas at Rs. 100 per square metre.
Solution:
Diameter of the base of the tent = 20 m
∴ Radius (r) =\((\frac { 20 }{ 2 } )\) = 10 m
Height of cylindrical part (h1) = 2.5 m
and height of conical part (h2) = 7.5 m
Slant height of the conical part (l)
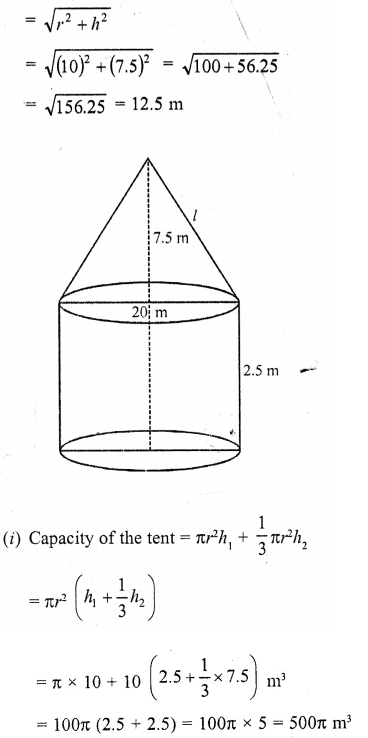

Question 12.
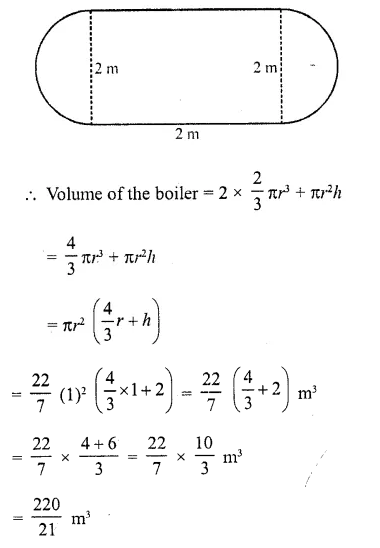
A boiler is in the form of a cylinder 2 m long with hemispherical ends each of 2 metre diameter. Find the volume of the boiler.
Solution:
Diameter of the cylinder = 2 m
∴ Radius (r) = \((\frac { 1 }{ 3 } )\) = 1 m
Height (length) of cylindrical part (h) = 2 m
Question 13.
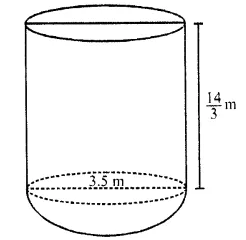
A vessel is a hollow cylinder fitted with a hemispherical bottom of the same base. The depth of the cylinder is \((\frac { 14 }{ 3 } )\) m and the diameter of hemisphere is 3.5 m. Calculate the volume and the internal surface area of the solid.
Solution:
Diameter of the cylindrical part = 3.5 m
∴Radius (r) = \((\frac { 3.5 }{ 2 } )\) = 1.75 = \((\frac { 7 }{ 4 } )\) m
and height (h) = \((\frac { 14 }{ 3 } )\) m

Question 14.
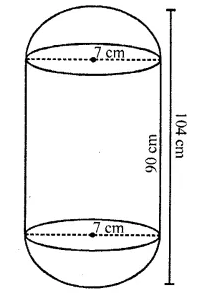
A solid is composed of a cylinder with hemispherical ends. If the whole length of the solid is 104 cm and the radius of each of the hemispherical ends is 7 cm, find the cost of polishing its surface at the rate of Rs. 10 per dm2 . (C.B.S.E. 2006C)
Solution:
Total height = 104 cm
Radius of hemispherical part (r) = 7 cm
Height of cylinder (h) = 104 cm – 2 x 7 cm = 104- 14 = 90 cm
Total outer surface area = curved surface area of the cylindrical part + 2 x curved surface area of each hemispherical part
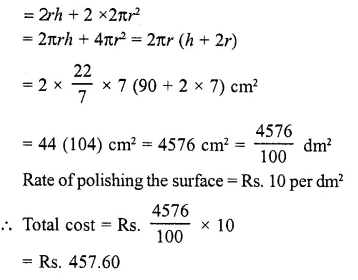
Question 15.
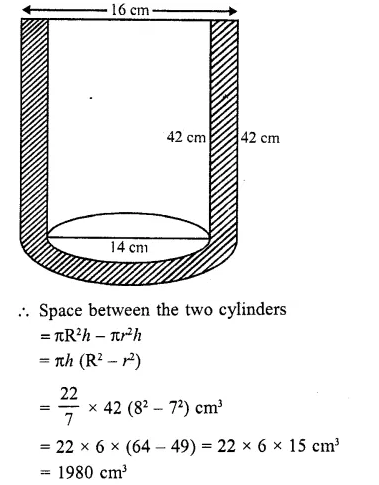
A cylindrical vessel of diameter 14 cm and height 42 cm is fixed symmetrically inside a similar vessel of diameter 16 cm and height 42 cm. The total space between the two vessels is filled with cork dust for heat insulation purposes. How many cubic centimeters of cork dust will be required ?
Solution:
Diameter of inner cylinder = 14 cm
∴Radius (r) = \((\frac { 14 }{ 2 } )\) = 7 cm
Diameter of outer cylinder = 16 cm
∴ Radius (R) = \((\frac { 16 }{ 2 } )\) = 8 cm
Height (h) = 42cm
Question 16.
A cylindrical road roller made of iron is 1 m long. Its internal diameter is 54 cm and the thickness of the iron sheet used in making the roller is 9 cm. Find the mass of the roller, if 1 cm³ of iron has 7.8 gm mass. (Use π = 3.14)
Solution:
Length of roller (h) = 1 m = 100 cm
Inner diameter = 54 cm
Thickness of iron sheet = 9 cm
∴ Inner radius (r) = \((\frac { 52 }{ 2 } )\) = 27 cm
and outer radus (R) = 27 + 9 = 36 cm
∴ Volume of the mass = πR²h – πr²h
= πh (R²- r²)
= 3.14 x 100 (36² – 27²) cm3
= 314 x (36 + 27) (36- 27) cm3
= 314 x 63 x 9 cmc
= 178038 cm3
Weight of 1 cm3 of iron = 7.8 gm
∴ Total weight = 178038 x 7.8 gm
= 1388696.4 gm
= 1388.6964 kg
= 1388.7 kg
Question 17.
A vessel in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is 14 cm and the total height of the vessel is 13 cm. Find the inner surface area of the vessel.
Solution:
Diameter of hemisphere = 14 cm
Total height =13 cm
Radius of hemisphere = \((\frac { 14 }{ 2 } )\) = 7 cm
∴ Height of cylindrical part =13-7 = 6 cm
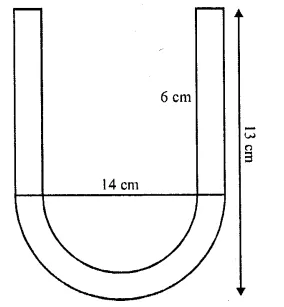
∴ Inner surface area of the vessel = inner surface area of cylindrical part + inner surface area of hemispherical part
Question 18.
A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy.
Solution:
Radius of cone (r) – 3.5 cm
Total height of the toy = 15.5 cm
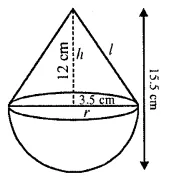
Height of the conical part (h) = 15.5 – 3.5 = 12 cm
∴ Slant height of the cone (l)

Question 19.
The difference between outside and inside surface areas of cylindrical metallic pipe 14 cm long is 44 m2. If the pipe is made of 99 cm3 of metal, find the outer and inner radii of the pipe.
Solution:
In cylindrical metallic pipe,
length of pipe = 14 cm
Difference between outside and inside
surface area = 44 m2
Volume of pipe material = 99 cm3
Let R and r be the outer and inner radii of the pipe respectively, then Outer surface area – inner surface area = 44 cm2
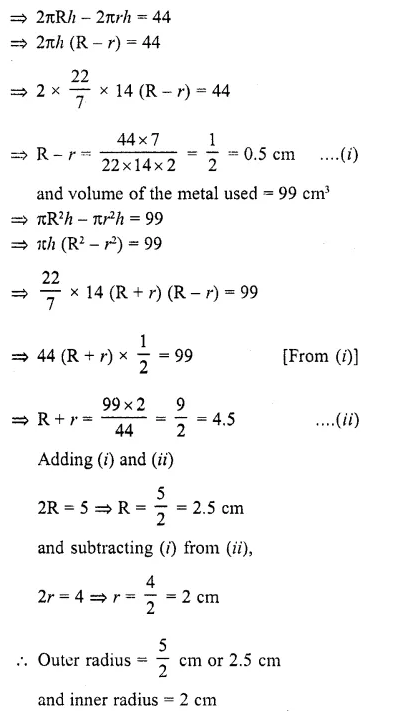
Question 20.
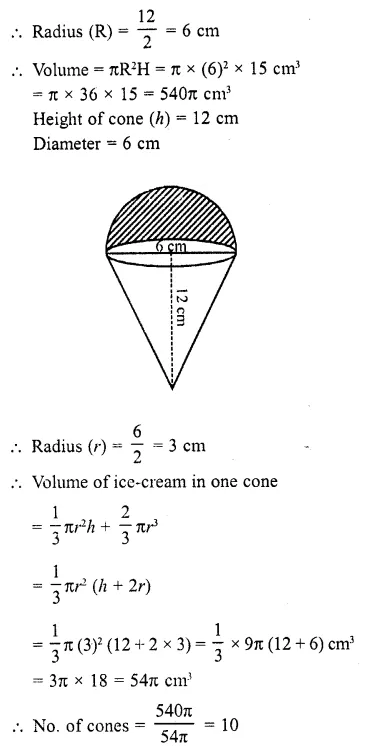
A right circular cylinder having diameter 12 cm and height 15 cm is full ice-cream. The ice-cream is to be filled in cones of height 12 cm and diameter 6 cm having a hemispherical shape on the top. Find the number of such cones which can be filled with ice-cream.
Solution:
Height of cylinder (H) = 15 cm
and diameter =12 cm
Question 21.
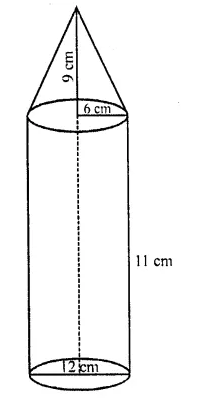
A solid iron pole having cylindrical portion 110 cm high and of base diameter 12 cm is surmounted by a cone 9 cm high. Find the mass of the pole, given that the mass of 1 cm3 of iron is 8 gm.
Solution:
Diamter of the base = 12 cm
∴ Radius (r) = \((\frac { 12 }{ 2 } )\) = 6 cm
Height of the cylindrical portion (h1)= 110 cm
and height of conical portion (h2) = 9 cm
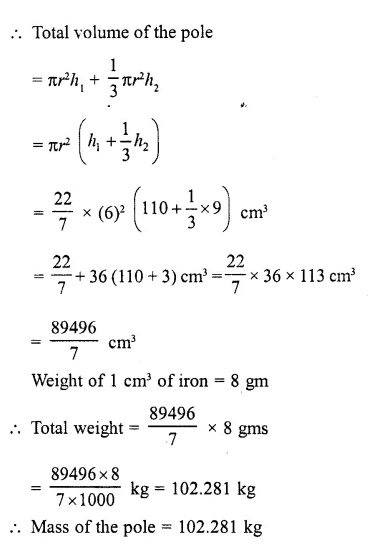
Question 22.
A solid toy is in the form of a hemisphere surmounted by a right circular cone. Height of the cone is 2 cm and the diameter of the base is 4 cm. If a right circular cylinder circumscribes the toy, find how much more space it will cover.
Solution:
Height of conical part (h) = 2 cm
Diameter of base = 4 cm
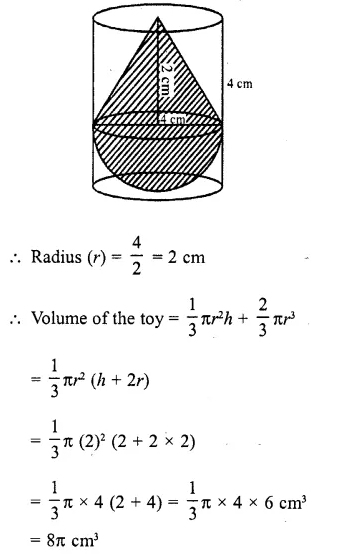
Now volume of the cylinder which circum scribes the toy = πr²h
= π (2)² x 4 = 16π cm³
∴ Difference of their volumes = 16π – 8π = 8πcm³
Question 23.
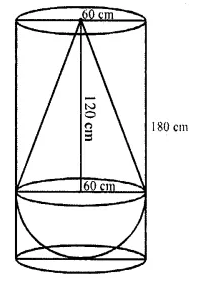
A solid consisting of a right circular cone of height 120 cm and radius 60 cm standing on a hemisphere of radius 60 cm is placed upright in a right circular cylinder full of water such that it touches the bottoms. Find the volume of water left in the cylinder, if the radius of the cylinder is 60 cm and its height is 180 cm.
Solution:
Radius of conical part = 60 cm
and height (h) = 120 cm
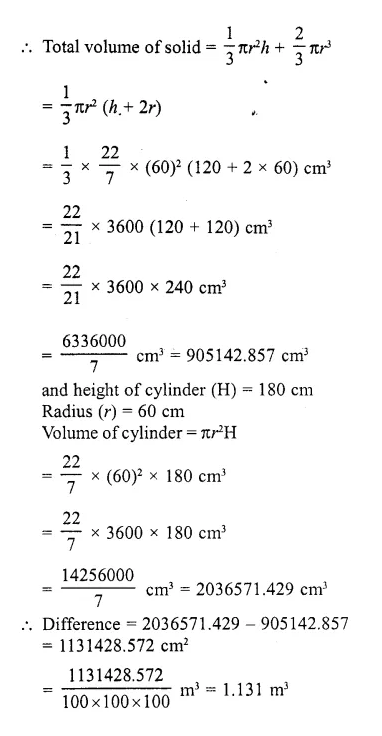
Question 24.
A cylindrical vessel with internal diameter 10 cm and height 10.5 cm is full of water. A solid cone of base diameter 7 cm and height 6 cm is completely immersed in water. Find the value of water (i) displaced out of the cylinder. (ii) left in the cylinder. (C.B.S.E. 2009)
Solution:
Internal diameters of cylindrical vessel = 10 cm
∴ Radius (r) = \((\frac { 10 }{ 2 } )\) =5 cm
and height (h) = 10.5 cm
∴ Volume of water filled in it

Question 25.
A hemispherical depression is cut out from one face of a cubical wooden block of edge 21 cm, such that the diameter of the hemisphere is equal to the edge of the cube. Determine the volume and total surface area of the remaining block. [CBSE 2010]
Solution:
Edge of cube = 21 cm
∴ Diameter of the hemisphere curved out of

Question 26.
A toy is in the form of a hemisphere surmounted by a right circular cone of the same base radius as that of the hemisphere. If the radius of the base of the cone is 21 cm and its volume is 2/3 of the volume of the hemisphere, calculate the height of the cone and the surface area of the toy. (Use π = 22/7).
Solution:
Radius of base of the conical part (r) = 21 cm


Question 27.
A solid is in the shape of a cone surmounted on a hemi-sphere, the radius of each of them is being 3.5 cm and the total height of solid is 9.5 cm. Find the volume of the solid. [CBSE 2012]
Solution:
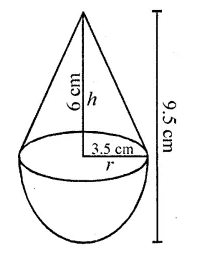

Question 28.
An wooden toy is made by scooping out a hemisphere of same radius from each end of a solid cylinder. If the height of the cylinder is 10 cm, and its base is of radius
3.5 cm, find the volume of wood in the toy. (Use π = 22/7). [CBSE 2013]
Solution:
Height of cylindrical part (h) = 10 cm
Radius of the base (r) = 3.5 cm

Question 29.
The largest possible sphere is carved out of a wooden solid cube of side 7 cm. Find the volume of the wood left. (Use π = 22/7). [CBSE 2014]
Solution:
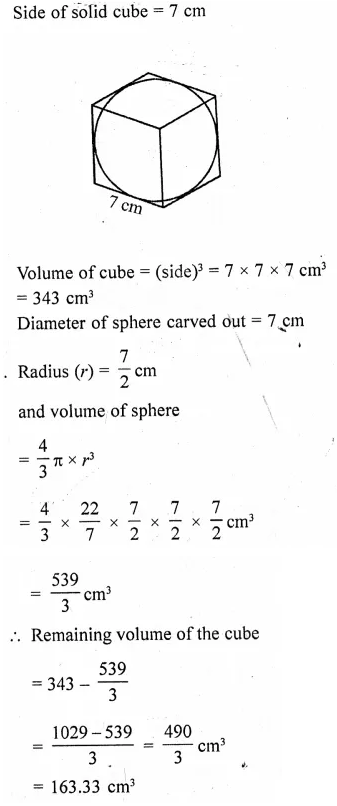
Question 30.
From a solid cylinder of height 2.8 cm and diameter 4.2 cm, conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid, (take π = 22/7). [CBSE 2014]
Solution:
Diameter of solid cylinder= 4.2 cm
∴ Radius (r) =\((\frac { 4.2 }{ 2 } )\) = 2.1 cm
Height (h) = 2.8 cm

Question 31.
The largest cone is curved out from one face of solid cube of side 21 cm. Find the volume of the remaining solid. [CBSE 2015]
Solution:
Side of a solid cube (a) = 21 cm
∴ Volume = a3, = (21 )3 cm3
= 9261 cm3
Diameter of the base of cone = 21 cm
Now radius of cone curved from it (r) =\((\frac { 21 }{ 2 } )\) cm
and height (h) = 21 cm
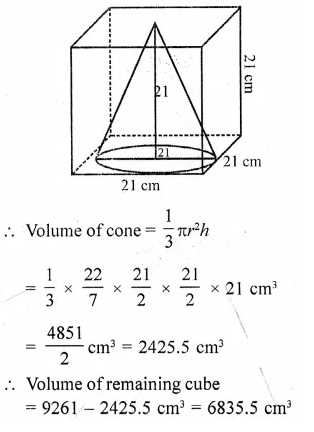
Question 32.
A solid wooden toy is in the form of a hemisphere surmounted by a Cone of same radius. The radius of hemisphere is 3.5 cm and the total wood used in the making of toy is 166 \((\frac { 5 }{ 6 } )\) cm3 . Find the height of the toy. Also, find the cost of painting the hemispherical part of the toy at the rate of ₹10 per cm2. (Take π = 22/7). [CBSE 2015]
Solution:
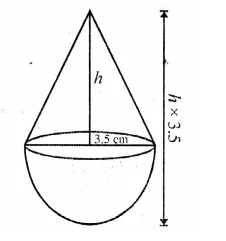
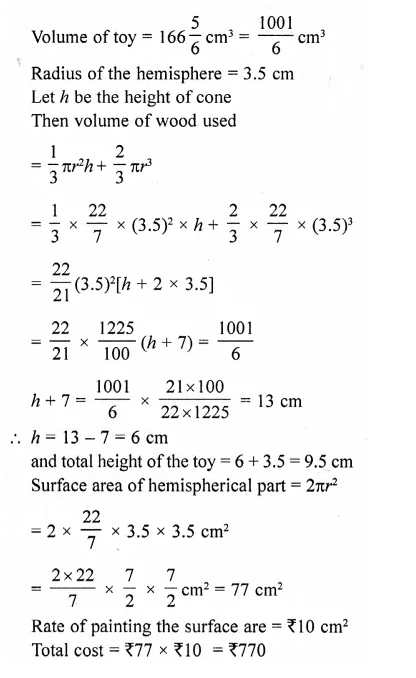
Question 33.
In the given figure, from a cuboidal solid metalic block, of dimensions 15 cm x 10 cm x 5 cm, a cylindrical hole of diameter 7 cm is drilled out. Find the surface area of the remaining block. (Take π = 22/7) [CBSE 2015]
Solution:
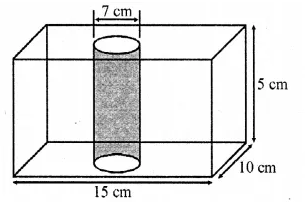
Radius of hole = \((\frac { 7 }{ 2 } )\)cm and height = 5 cm
Length of block (l) = 15 cm
Breadth (b) = 10 cm and height = 5 cm
∴ Surface area = 2(lb + bh + hl)
= 2(15 x 10 + 10 x 5 + 5 x 15) cm2
= 2(150 + 50 + 75) = 2 x 275 = 550 cm2
Area of circular holes of both sides = 2 x πr2

Question 34.
A building is in the form of a cylinder surmounted by a hemi-spherical vaulted dome and
contains 41 \((\frac { 19 }{ 21 } )\) m3 of air. If the internal diameter of dome is equal to its total height above the floor, find the height of the building? [NCERT Exemplar]
Solution:
Let total height of the building = Internal diameter of the dome = 2rm
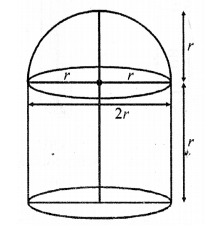
Radius of building (or dome) = \((\frac { 2r }{ 2 } )\) = r m
Height of cylinder = 2r-r = rm
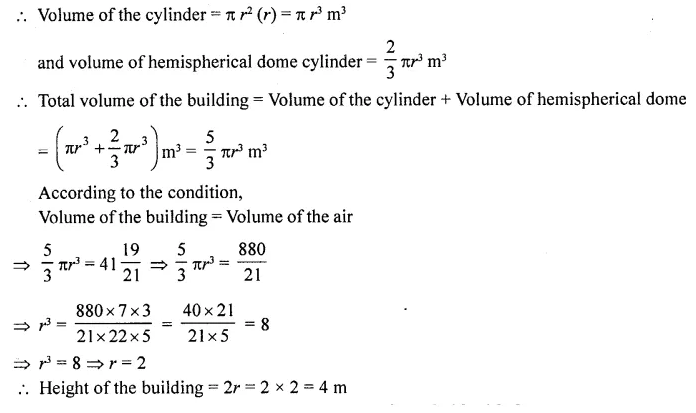
Question 35.
A pen stand made of wood is in the shape of a cuboid with four conical depressions and a cubical depression to hold the pens and pins, respectively. The dimension of the cuboid are 10 cm x 5 cm x 4 cm. The radius of each of the conical depression is 0.5 cm and the depth is 2.1 cm. The edge of the cubical depression is 3 cm. Find the volume of the wood in the entire stand. [NCERT Exemplar]
Solution:
Given that, length of cuboid pen stand (l) = 10 cm
Breadth of cuboid pen stand (b) = 5 cm
and height of cuboid pen stand (h) = 4 cm
∴ Volume of cuboid pend stand = l x b x h= 10 x 5 x 4 = 200 cm3
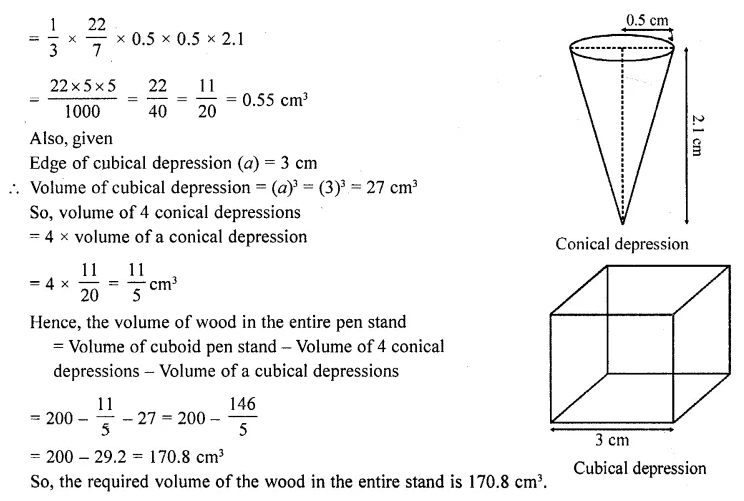
Also, radius of conical depression (r) = 0.5 cm
and height (depth) of a conical depression (h1) = 2.1 cm
∴ Volume of a conical depression = πrh1
Question 36.
A building is in the form of a cylinder surmounted by a hemispherical dome. The base diameter of the dome is equal to \((\frac { 2 }{ 3 } )\) of the total height of the building. Find the height of the building, if it contains 67 \((\frac { 1 }{ 21 } )\) m3 of air.
Solution:
Let the radius of the hemispherical dome be r metres and the total height of the building be h metres.
Since the base diameter of the dome is equal to \((\frac { 2 }{ 3 } )\) of the total height, therefore
2 r = \((\frac { 2 }{ 3 } )\)h. This implies r = \((\frac { h }{ 3 } )\). Let H metres be the height of the cylindrical portion.
Therefore, H = h – \((\frac { h }{ 3 } )\) = \((\frac { 2 }{ 3 } )\)h metres.
Volume of the air inside the building = Volume of air inside the dome + Volume of the air inside the
cylinder = \((\frac { 2 }{ 3 } )\) πr3 + πr2H, where H is the height of the cylindrical portion

Question 37.
A solid toy is in the form of a hemisphere surmounted by a right circular cone. The height of cone is 4 cm and the diameter of the base is 8 cm. Determine the volume of the toy. If a cube circumscribes the toy, then find the difference of the volumes of cube and the toy. Also, find the total surface area of the toy. [NCERT Exemplar]
Solution:
Let r be the radius of the hemisphere and the cone and h be the height of the cone.
Volume of the toy=Volume of the hemisphere + Volume of the cone
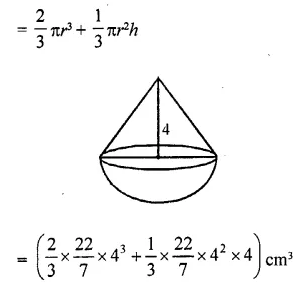
= \((\frac { 1408 }{ 7 } )\) cm3
A cube circumsrcibes the given solid. Therefore, edge of the cube should be 8 cm. Volume of the cube = 83 cm3 = 512 cm3 Difference in the volume of the cube and

Question 38.
A circus tent is in the shape of a cylinder surmounted by a conical top of same diameter. If their common diameter is 56 m, the height of the cylindrical part is 6 m and the total height of the tent above the ground is 27 m, find the area of the canvas used in making the tent. [ICBSE 2017]
Solution:
We have, diameter of base of cylinder = d = 56 m
Radius of base of cylinder = r= \((\frac { d }{ 2 } )\)= \((\frac { 52 }{ 2 } )\)= 28 m
Height of tent = 27 m
Height of cylinder = 6 m
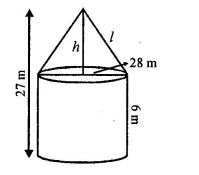
Height of conical portion = 27 – 6 = 21 m
Radius of conical portion, r = 28 m

Hope given RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.