RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise
These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise
Other Exercises
- RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1
- RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2
- RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3
- RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise
- RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS
- RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS
Question 1.
A metallic sphere 1 dm in diameter is beaten into a circular sheet of uniform thickness equal to 1 mm. Find the radius of the sheet.
Solution:
Diameter of a sphere = 1 dm = 10 cm
∴ Radius (r) = \((\frac { 10 }{ 2 } )\) = 5 cm
Volume of metal used in the sphere = \((\frac { 4 }{ 3 } )\) πr³
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise

Question 2.
Three solid spheres of radii 3,4 and 5 cm respectively are melted and converted into a single solid sphere. Find the radius of this sphere.
Solution:
Radius of first sphere (r1) = 3 cm
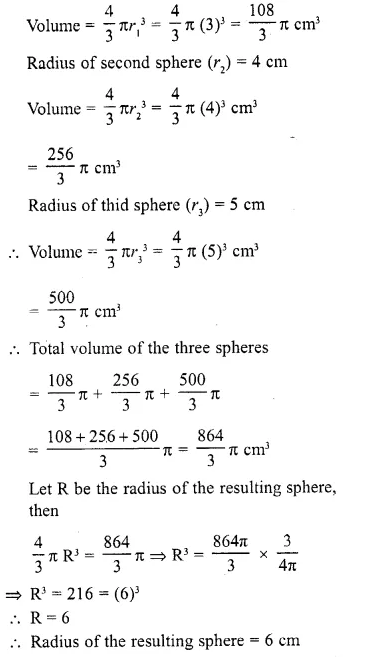
Question 3.
A spherical shell of lead, whose external diameter is 18 cm, is melted and recast into a right circular cylinder, whose height is 8 cm and diameter 12 cm. Determine the internal diameter of the shell.
Solution:
Diameter of the cylinder = 12 cm
∴ Radius (r1) = \((\frac { 12 }{ 2 } )\) = 6 cm
Height (h) = 8 cm
∴ Volume = πr1²h = π(6)² x 8 cm³
= π x 36 x 8 = 288π cm³
Now volume of metal used in spherical shell = 288π cm
External diameter = 18 cm 18
∴ External radius (R) = \((\frac { 18 }{ 2 } )\) = 9 cm
Let r be the internal radius, then
Volume of the metal = \((\frac { 4 }{ 3 } )\) π (R³ – r³ )
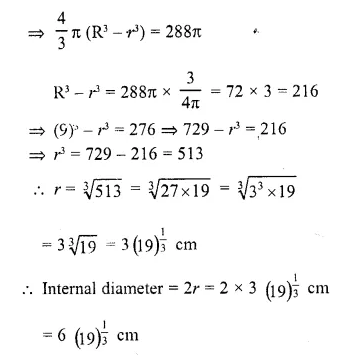
Question 4.
A well with 10 m inside diameter is dug 8.4 m deep. Earth taken out of it is spread all around it to a width of 7.5 m to form an embankment. Find the height of the embankment.
Solution:
Diameter of two well = 10 m
∴ Radius (r) = \((\frac { 10 }{ 2 } )\) = 5 m
Depth (h) = 8.4 m
∴ Volume of earth dug out = πr²h
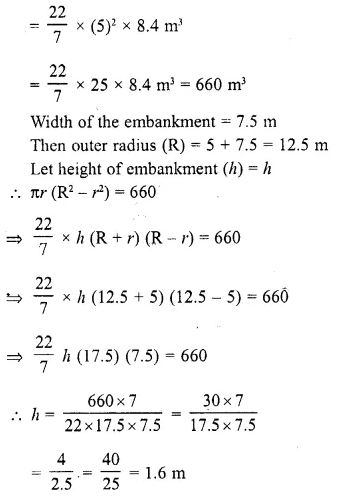
Question 5.
In the middle of a rectangular field measuring 30 m x 20 m, a well of 7 m diameter and 10 m depth is dug. The earth so removed is evenly spread over the remaining part of the field. Find the height through which the level of the field is raised.
Solution:
Diameter of well = 7 m
∴ Radius (r) = \((\frac { 7 }{ 2 } )\) m
Depth (h) = 10 m
∴ Volume of earth dug out = πr²h

Question 6.
The inner and outer radii of a hollow cylinder are 15 cm and 20 cm, respectively. The cylinder is melted and recast into a solid cylinder of the same height. Find the radius of the base of new cylinder.
Solution:
Inner radius of hollow cylinder (r) = 15 cm
Outer radius (R) = 20 cm
Let h be the height of the hollow cylinder,
Then volume of metal used = πR (R² – r²)
= πh (20²- 15²) cm³
= πh (400 – 225) cm³
= 175 πh cm³
Volume of the new cylinder = 175nh cm³
Height = h
Let R be the radius of new cylinder,
then πR²h = 175 πh
⇒ R²= 175
⇒ R = \(\sqrt { 175 } \)
= 13.2
∴ Radius = 13.2 cm
Question 7.
Two cylindrical vessels are filled with oil. Their radii are 15 cm, 12 cm and heights 20 cm, 16 cm respectively. Find the radius of a cylindrical vessel 21 cm in height, which will just contain the oil of the two given vessels.
Solution:
Radius of first cylinder (r1) = 15 cm
and radius of second cylinder (r2) = 12 cm
Height of the first cylinder (h1) = 20 cm
and height of second cylinder (h2) = 16 cm
∴ Volume of both of cylinders

Question 8.
A cylindrical bucket 28 cm in diameter and 72 cm high is full of water. The water is emptied into a rectangular tank 66 cm long and 28 cm wide. Find the height of the water level in the tank.
Solution:
Diameter of cylindrical bucket = 28 cm
∴ Radius (r) = \((\frac { 28 }{ 2 } )\) = 14 cm
Height (h) = 72 cm
∴ Volume of water filled in it = πr²h
= \((\frac { 22 }{ 7 } )\) x 14 x 14 x 72 cm³ = 44352 cm³
∴ Volume of water in rectangular tank = 44352 cm³
Length of tank (l) = 66 cm
and breadth (b) = 28 cm
Let h1 be its height
∴ Ibh1 = 44352
⇒ 66 x 28 h1= 44352
⇒ h1 = \((\frac { 44352 }{ 66×28 } )\) = 24
∴Height of water in the tank = 24 cm

Question 9.
A cubic cm of gold is drawn into a wire 0.1 mm in diameter, find the length of the wire.
Solution:
Volume of solid gold = 1 cm³
Diameter of cylinderical wire = 0.1 mm

Question 10.
A well of diameter 3 m is dug 14 m deep. The earth taken out of it is spread evenly all around it to a width of 4 m to form an embankment. Find the height of the embankment.
Solution:
Diameter of the well = 3 m
Radius (r) = \((\frac { 3 }{ 2 } )\) m
Depth (h) = 14 m
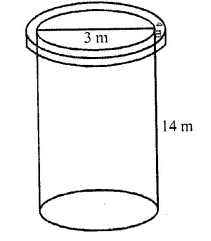

Question 11.
A conical vessel whose internal radius is 10 cm and height 48 cm is full of water. Find the volume of water. If this water is poured into a cylindrical vessel with internal radius 20 cm, find the height to which the water level rises in it.
Solution:
Internal radius of the conical vessel (r1) = 10 cm
Height (h1) = 48 cm

Question 12.
The vertical height of a conical tent is 42 dm and the diameter of its base is 5.4 m. Find the number of persons it can accommodate if each person is to be allowed 29.16 cubic dm.
Solution:
Vertical height of conical tent (h) = 42 dm
and diameter base (b) = 5.4 dm
∴ Radius (r) = \((\frac { 5.4 }{ 2 } )\) = 2.7 dm

Question 13.
A right circular cylinder and a right circular cone have equal bases and equal heights. If their curved surfaces are in the ratio 8 : 5, determine the ratio of the radius of the base to the height of either of them.
Solution:
Let r and h be the radius and height of a circular cylinder and also of a cone, then curved surface area of the cylinder = 2πrh
and curved surface area of cone
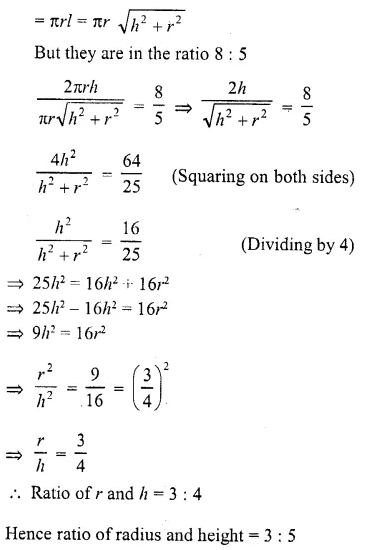
Question 14.
A sphere of diameter 5 cm is dropped into a cylindrical vessel partly filled with water. The diameter of the base of the vessel is 10 cm. If the sphere is completely submerged, by how much will the level of water rise ?
Solution:
Diameter of sphere = 5 cm
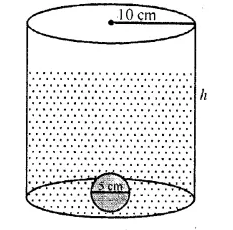
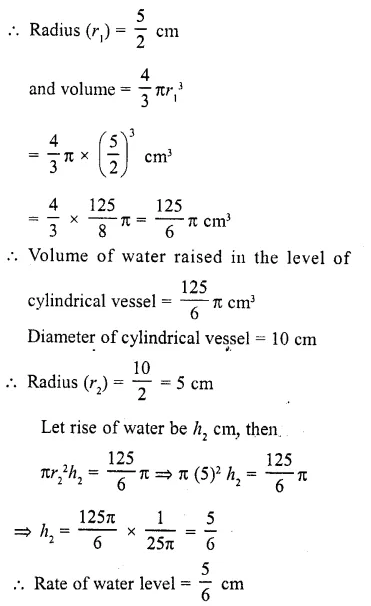
Question 15.
A spherical ball of iron has been melted – and made into smaller balls. If the radius of each smaller ball is one-fourth of the radius of the original one, how many such balls can be made ?
Solution:
Let the radius of larger ball = r
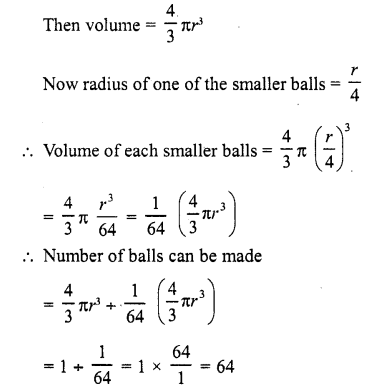
Question 16.
Find the depth of a cylindrical tank of radius 28 m, if its capacity is equal to that of a rectangular tank of size 28 m x 16 m x 11 m.
Solution:
Dimensions of a rectangular tank = 28m x 16m x 11m
∴ Volume = 28 x 16 x 11 m³ = 4928 m³
∴ Volume of cylindrical tank = 4928 m³
Radius of the cylindrical tank = 28 m
Let h be depth of the tank, then
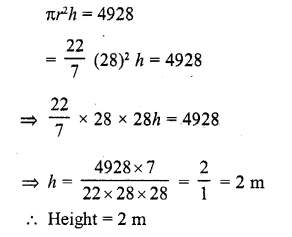
Question 17.
A hemispherical bowl of internal radius IS cm contains a liquid. The liquid is to be filled into cylindrical-shaped bottles of diameter S cm and height 6 cm. How many bottles are necessary to empty the bowl? (C.B.S.E. 2001C)
Solution:
Internal radius of hemispherical bowl (r) = 15 cm

Question 18.
In a cylindrical vessel of diameter 24 cm, filled up with sufficient quantity of water, a solid spherical ball of radius 6 cm is completely immersed. Find the increase in height of water level.
Solution:
Diameter of the cylindrical vessel = 24 cm

Question 19.
A hemisphere of lead of radius 7 cm is cast into a right circular cone of height 49 cm. Find the radius of the base.
Solution:
Radius of hemisphere of lead (r1) = 7 cm

Question 20.
A solid metallic sphere of diameter 28 cm is melted and recast into a number of smaller cones, each of diameter 4\((\frac { 2 }{ 3 } )\)cm and height 3 cm. Find the number of cones so formed. (C.B.S.E. 2004)
Solution:
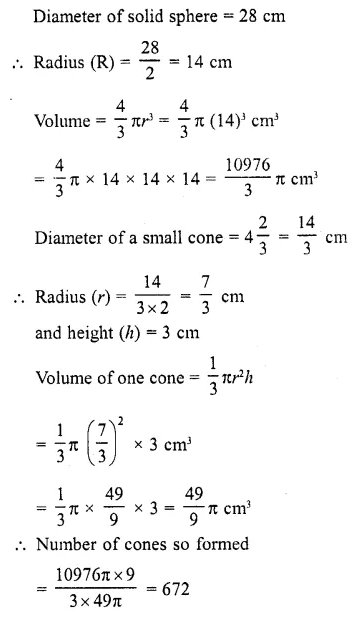
Question 21.
The diameter of a copper sphere is 18 cm. The sphere is melted and is drawn into a long wire of uniform circular cross section. If the length of the wire is 108 m, find its diameter. (C.B.S.E. 1994)
Solution:
Diameter of copper sphere – 18 cm 18
Radius (R) = \((\frac { 18 }{ 2 } )\) = 9 cm 4
Volume = \((\frac { 4 }{ 3 } )\) π (R³)

Question 22.
A hemisphere of lead of radius 7 cm is cast into a right circular cone of height 49 cm. Find the radius of the base.
Solution:
Radius of hemisphere (R) = 7 cm

Question 23.
A metallic sphere of radius 10.5 cm is melted and thus recast into small cones, each of radius 3.5 cm and height 3 cm. Find how many cones are obtained. (C.B.S.E. 2004)
Solution:
Radius of sphere (R) = 10.5 cm
∴ Volume of sphere =\((\frac { 4 }{ 3 } )\) πR³
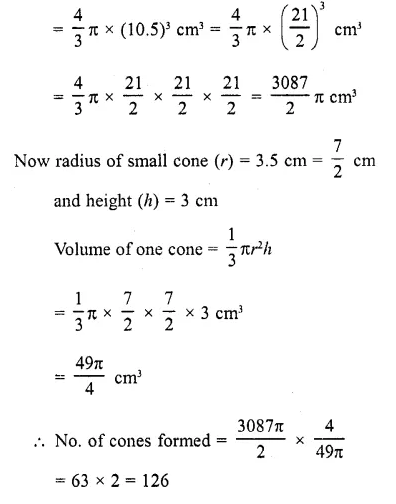
Question 24.
A cone, a hemisphere and a cylinder stand on equal bases and have the same height. Show that their volumes are in the ratio 1:2:3.
Solution:
Let radius of a cone, a hemisphere and a cylinder be r
and height in each case = h
∴ h = r

Question 25.
A hollow sphere of internal and external diameters 4 and 8 cm respectively is melted into a cone of base diameter 8 cm. Find the height of the cone.
Solution:
Outer diameter of a hollow sphere = 8 cm
∴ Outer radius (R) = \((\frac { 8 }{ 2 } )\) = 4 cm
and inner diameter = 4 cm
∴ Inner radius (r)=\((\frac { 4 }{ 2 } )\) =2 cm

Question 26.
The largest sphere is carved out of a cube of the side 10.5 cm. Find the volume of the sphere.
Solution:
Side of a cube = 10.5 cm
∵ The largest sphere is carved out of the cube,
∴ Diameter of the cube = side of the cube = 10.5 cm

Question 27.
Find the weight of a hollow sphere of metal having internal and external diameters as 20 cm and 22 cm, respectively if 1 cm³ of metal weighs 21 g.
Solution:
Internal diameter of a hollow sphere = 20 cm
and external diameter = 22 cm
∴ Outer radius (R) = \((\frac { 22 }{ 2 } )\) = 11 cm 20
and inner radius = \((\frac { 20 }{ 2 } )\) = 10 cm

Question 28.
A solid sphere of radius ‘r’ is melted and recast into a hollow cylinder of uniform thickness. If the external radius of the base of the cylinder is 4 cm, its height 24 cm and thinkness 2 cm, find the value of ‘r’.
Solution:
Radius of solid sphere = r
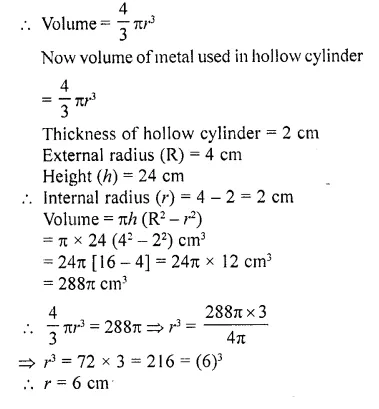
Question 29.
Lead spheres of diameter 6 cm are dropped into a cylindrical beaker containing some water and are fully submerged. If the diameter of the beaker is 18 cm and water rises by 40 cm find the number of lead spheres dropped in the water.
Solution:
Diameter of cylindrical diameter = 18 cm

Question 30.
The height of a solid cylinder is 15 cm and the diameter of its base is 7 cm. Two equal conical holes each of radius 3 cm and height 4 cm arc cut off. Find the volume of the remaining solid.
Solution:
Diameter of right solid cylinder = 7 cm

Question 31.
A solid is composed of a cylinder with hemispherical ends. If the length of the whole solid is 108 cm and the diameter of the cylinder is 36 cm, find the cost of polishing the surface at the rate of 7 paise per cm2. (Use TC = 3.1416)
Solution:
Total height of the solid =108 cm
Each diameter of base of hemispherical part = 36 cm

Question 32.
The surface area of a sphere is the same as the curved surface area of a cone having the radius of the bases as 120 cm and height 160 cm. Find the radius of the sphere.
Solution:

Question 33.
A right circular cylinder and a right circular cone have equal bases and equal heights. If their curved surfaces are in the ratio 8 : 5, determine the ratio of the radius of the base to the height of either of them.
Solution:
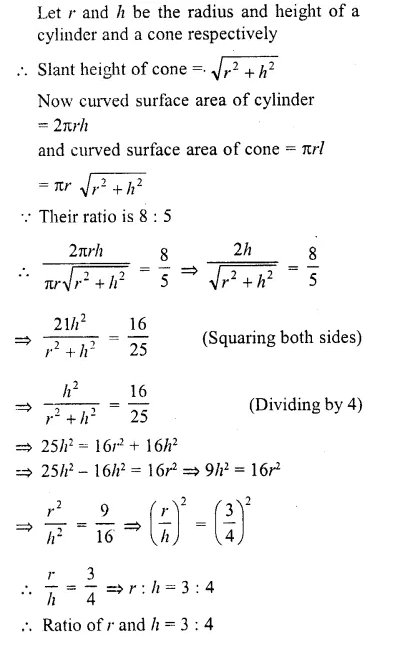
Question 34.
A rectangular vessel of dimensions 20 cm x 16 cm x 11 cm is full of water. This water is poured into a conical vessel. The top of the conical vessel has its radius 10 cm. If the conical vessel is filled completely, determine its height. (Use π = 22/7)
Solution:
Dimension of rectangular vessel are 20 cm x 16 cm x 11 cm
Volume of vessel = 20 x 16 x 11 cm³= 3520 cm³
∴ Volume of water in conical vessel = 3520 cm³
Radius of the top of vessel = 10 cm
Let h be its height, then

Question 35.
If r1 and r2 be the radii of two solid metallic spheres and if they are melted into one solid sphere, prove that the radius of the new sphere is (r1³ + r1³ )1/3.
Solution:

Question 36.
A solid metal sphere of 6 cm diameter is melted and a circular sheet of thickness 1 cm is prepared. Determine the diameter of the sheet.
Solution:
Diameter of solid sphere = 6 cm 6

Question 37.
A hemispherical tank full of water is \((\frac { 25 }{ 7 } )\) emptied by a pipe at the rate of litres per second. How much time will it take to half-empty the tank, if the tank is 3 metres in diameter ?
Solution:
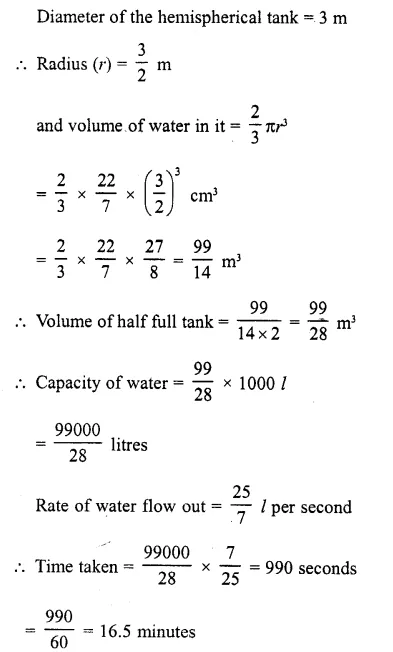
Question 38.
Find the number of coins, 1.5 cm is diameter and 0.2 cm thick, to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.
Solution:

Question 39.
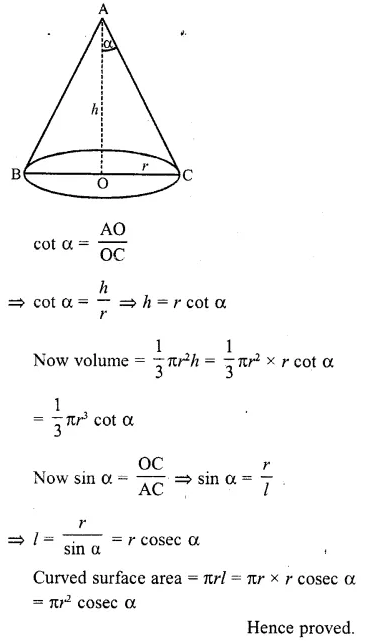
The radius of the base of a right circular cone of semi-vertical angle a is r. Show that its volume is \((\frac { 1 }{ 3 } )\) πr³ cot a and curved surface area is πr² cosec α.
Solution:
Radius of circular cone = r
and semi vertical angle = α
Let AO = h and slant height AC = l
In ΔAOC, AO ⊥ BC
Question 40.
An iron pillar consists of a cylindrical portion 2.8 m high and 20 cm in diameter and a cone 42 cm high is surmounting it. Find the weight of the pillar, given that 1 cubic cm of iron weighs 7.5 gm.
Solution:
Diameter of cylindrical portion = 20 cm
∴ Radius (r) = \((\frac { 20 }{ 2 } )\) = 10 cm
Height of (h1) = 2.8 m = 280 cm
and height of cone (h2) = 42 cm

Question 41.
A circus tent is cylindrical to a height of 3 metres and conical above it. If its diameter is 105 m and the slant height of the conical portion is 53 m, calculate the length of the canvas 5 m wide to make the required tent.
Solution:
Diameter of the tent = 105 m
∴ Radius (r) = \((\frac { 105 }{ 2 } )\) m
Height of cylindrical part (h1) = 3m
Slant height of conical part (h2) – 53 m
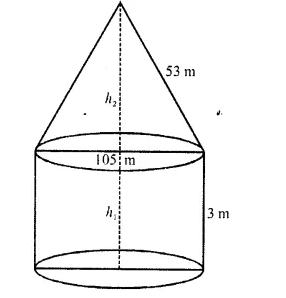
∴ Total surface area of the tent = curved surface area of the conical part + curved surface area of the cylindrical area
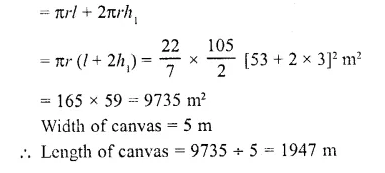
Question 42.
Height of a solid cylinder is 10 cm and diameter 8 cm. Two equal conical hole have been made from its both ends. If the diameter of the holes is 6 cm and height 4 cm, find (i) volume of the cylinder, (ii) volume of one conical hole, (iii) volume of the remaining solid.
Solution:
Height of the solid cylinder (h1) = 10 cm
Diameter = 8 cm
∴Radius (r1) = \((\frac { 8 }{ 2 } )\) = 4 cm
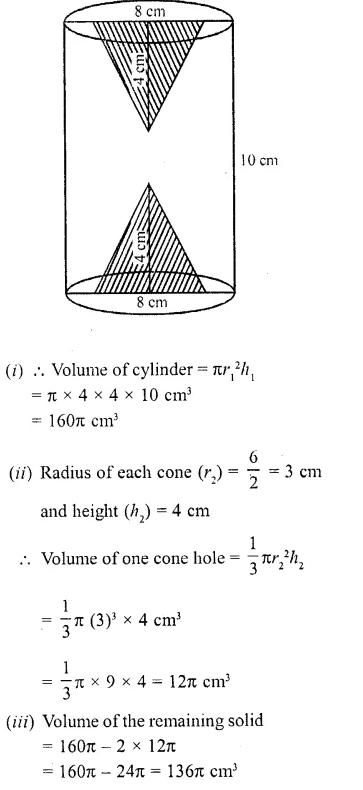
Question 43.
The height of a solid cylinder is 15 cm and the diameter of its base is 7 cm. Two equal conical holes each of radius 3 cm, and height 4 cm are cut off. Find the volume of the remaining solid.
Solution:
Diameter of the base of a cylinder = 7 cm
∴ Radius (r1) = \((\frac { 7 }{ 2 } )\) cm
Height of cylinder (h1) = 15 cm

Question 44.
A solid is composed of a cylinder with hemispherical ends. If the length of the whole solid is 108 cm and the diameter of the cylinder is 36 cm, find the cost of polishing the surface at the rate of 7 paise per cm2. (Useπ = 3.1416)
Solution:
Total height of the solid =108 cm
Diameter of base of each hemisphere = 36 cm

Question 45.
The largest sphere is to be curved out of a right circular cylinder of radius 7 cm and height 14 cm. Find the volume of the sphere.
Solution:
Radius of cylinder (r) = 7 cm
and height (h) = 14 cm
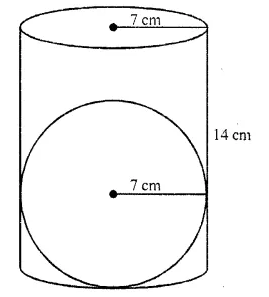
The diameter of the largest sphere curved out of the given cylinder = diameter of the cylinder
= 2 x 7 = 14 cm
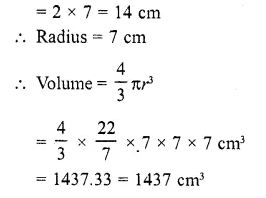
Question 46.
A tent is in the form of a right circular cylinder surmounted by a cone. The diameter of the base of the cylinder or the cone is 24 m. The height of the cylinder is 11 m. If the vertex of the cone is 16 m above the ground, find the area of the canvas required for making the tent. (Use π = 22/7)
Solution:
Diameter of the base of the cone = 24 m
∴ Radius (r) = \((\frac { 24 }{ 2 } )\) = 12 m
Height of the cylindrical part (h1) = 11 m
Total height of the tent = 16 m
Height of the conical part (h2)
= 16- 11 = 5 m
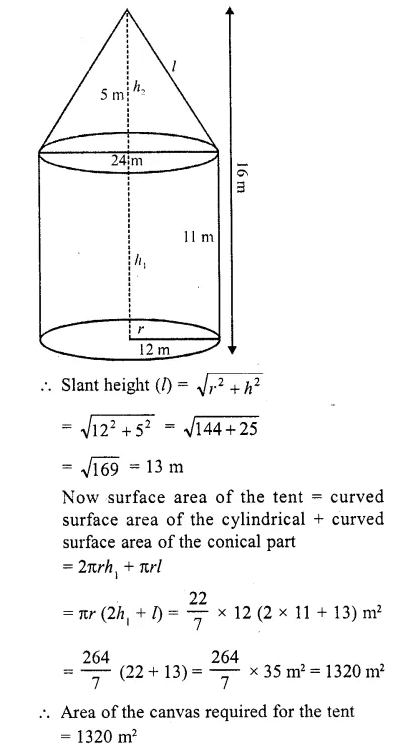
Question 47.
Area of the canvas required for the tent = 1320 m2 47. A toy is in the form of a cone mounted on a hemisphere of radius 3.5 cm. The total height of the toy is 15.5 cm find the total surface area and volume of the toy. (C.B.S.E. 2000, 2002)
Solution:
Radius of the toy (r) = 3.5 cm
Total height of the toy = 15.5 cm
∴ Height of the conical part = 15.5 – 3.5 = 12 cm
Slant height of the conical part (l)
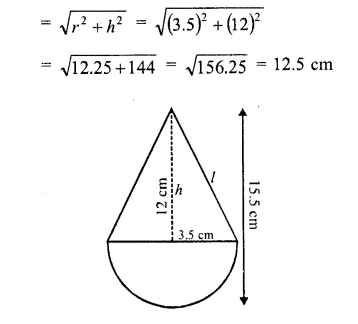
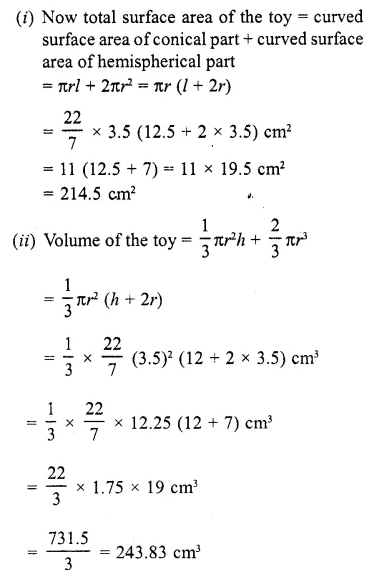
Question 48.
A cylindrical container is filled with ice-cream, whose diameter is 12 cm and height is 15 cm. The whole ice-cream is distributed to 10 children in equal cones having hemispherical tops. If the height of the conical portion is twice the diameter of its base, find the diameter of the ice-cream.
Solution:
Diameter of the cylindrical container = 12 cm
Radius (r1) = \((\frac { 12 }{ 2 } )\) = 6 cm
Height (h1) = 15 cm

Question 49.
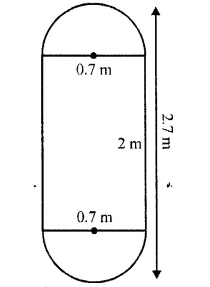
Find the volume of a solid in the form of a right circular cylinder with hemi-spherical ends whose total length is 2.7 m and the diameter of each hemispherical end is 0.7 m.
Solution:
Total length of solid = 2.7 m
Diameter of each hemisphere at the ends = 0.7 cm

Question 50.
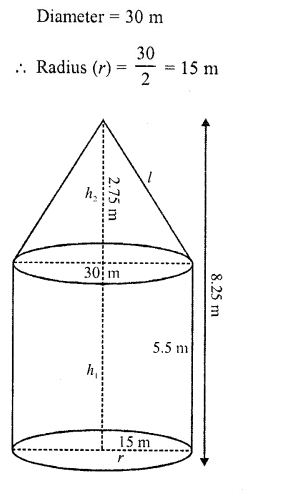
A tent of height 8.25 m is in the form of a right circular cylinder with diameter of base 30 m and height 5.5 m, surmounted by a right circular cone of the same base. Find the cost of the canvas of the tent at the rate of Rs. 45 per m².
Solution:
Total height of the tent = 8.25 m
Height of cylindrical part (h1) = 5.5 m
∴ Height of conical part (h2) = 8.25 – 5.5 = 2.75m

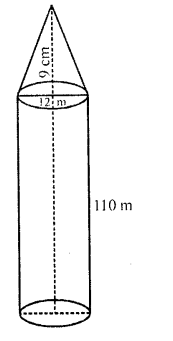
Question 51.
An iron pole consisting of a cylindrical portion 110 cm high and of base diameter 12 cm is surmounted by a cone 9 cm high. Find the mass of the pole, given that 1 cm³ of iron has 8 gram mass approximately. (Use π = 355/115)
Solution:
Diameter of the base of the cylindrical pole = 12 cm
∴ Radius (r) = \((\frac { 12 }{ 2 } )\) = 6 cm
Height of cylindrical portion (h1) = 110 cm
and height of conical portion (h2) = 9 cm

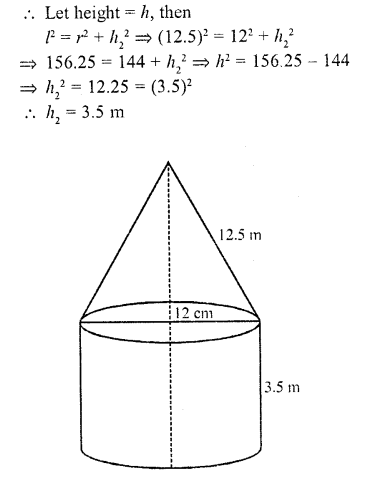
Question 52.
The interior of a building is in the form of a cylinder of base radius 12 m and height 3.5 m, surmounted by a cone of equal base and slant height 12.5 m. Find the internal curved surface area and the capacity of the building.
Solution:
Radius of the building (r) = 12m
Height of the cylindrical portion (h1) = 3.5 m and
slant height of conical portion (l) = 12.5 m
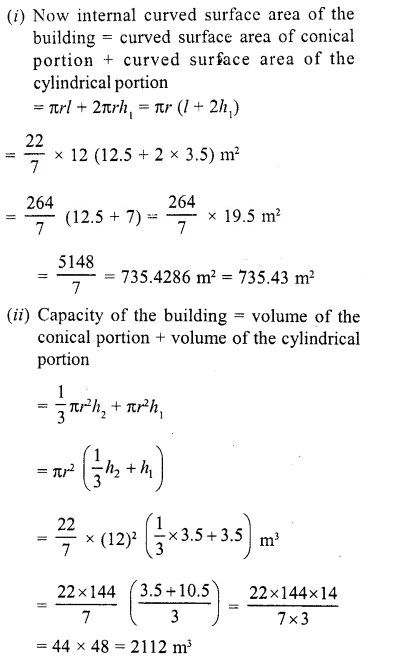
Question 53.
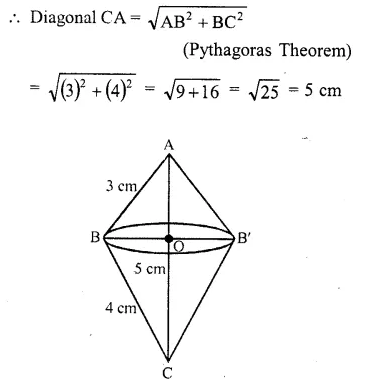
A right angled triangle with sides 3 cm and 4 cm is revolved around its hypotenuse. Find the volume of the double cone thus generated.
Solution:
In right angled ΔABC, ∠B = 90°
AB = 3 cm and BC = 4 cm
Now revolving the triangle along CA,

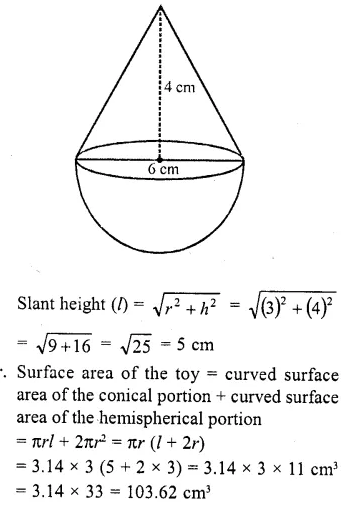
Question 54.
A toy is in the form of a cone mounted on a hemisphere with the same radius. The diameter of the base of the conical portion is 6 cm and its height is 4 cm. Determine the surface area of the toy (Use π = 3.14).
Solution:
Diameter of the base of the toy = 6 cm
∴ Radius (r) = \((\frac { 6 }{ 2 } )\) = 3 cm
Height of conical portion (h) = 4 cm
Question 55.
Find the mass of a 3.5 m long lead pipe, if the external diameter of the pipe is 2.4 cm, thickness of the metal is 2 mm and the mass of 1 cm3 of lead is 11.4 grams.
Solution:
External diameter of a cylindrical pipe = 2.4 cm
Radius (R) = \((\frac { 2.4 }{ 2 } )\) = 1.2 cm
Thickness of the pipe = 2 mm =\((\frac { 2 }{ 10 } )\) = 0.2 cm
∴ Inner radius (r) = 1.2 – 0.2 = 1.0 cm
Height (length) of the pipe (h) = 3.5 m
= 350 cm
Volume of the mass of the pipe = πh (R² – r²)

Question 56.
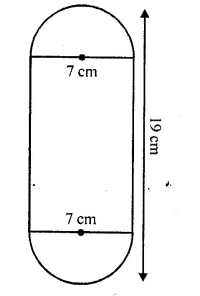
A solid is in the form of a cylinder with hemispherical ends. Total height of the solid is 19 cm and the diameter of the cylinder is 7 cm. Find the volume and total surface area of the solid.
Solution:
Total height of the solid = 19 cm
Diameter of the cylinder = 7 cm
Radius (r) = \((\frac { 7 }{ 2 } )\) cm
Height of the cylinder = 19 – 2 x \((\frac { 7 }{ 2 } )\) cm
= 19-7 =12cm

Question 57.
A golf ball has diameter equal to 4.2 cm. Its surface has 200 dimples each of radius 2 mm. Calculate the total surface area which is exposed to the surroundings assuming that the dimples are hemi-spherical.
Solution:
Diameter of the golf ball = 4.2 cm
∴ Radius (R) = \((\frac { 4.2 }{ 2 } )\) =2.1 cm
Radius of each hemispherical dimples (r) = 2 mm = \((\frac { 2 }{ 10 } )\) = \((\frac { 2 }{ 5 } )\) cm
Curved surface area of one dimple = 2πr²
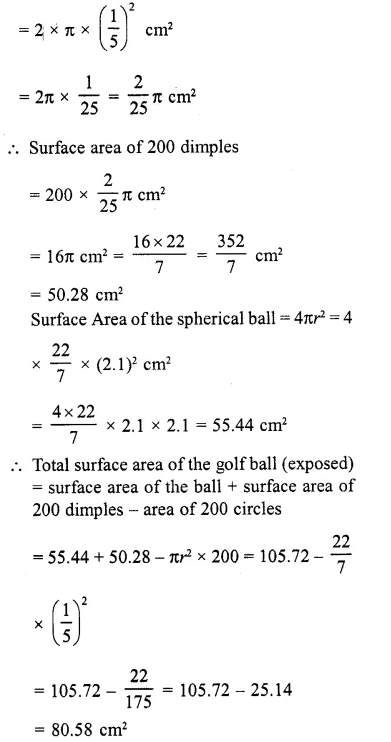
Question 58.
The radii of the ends of a bucket of height 24 cm are 15 cm and 5 cm. Find its capacity. (Take π = 22/7).
Solution:
Height of the bucket (frustum) (h) = 24 cm
Upper radius (r1) = 15 cm
and lower radius (r2) = 5 cm
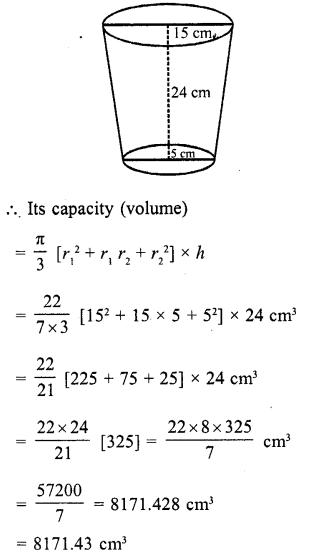
Question 59.
The radii of the ends of a bucket 30 cm high are 21 cm and 7 cm. Find its capacity in litres and the amount of sheet required to make this bucket.
Solution:
Height of the bucket (frustum) (h) = 30 cm
Upper radius (r1) = 21 cm
and lower radius (r2) = 7 cm


Question 60.
The radii of the ends of a frustum of a right circular cone are 5 metres and 8 metres and its lateral height is 5 metres. Find the lateral surface and volume of the frustum.
Solution:
Upper radius of a frustum (r1) = 8 m
and lower radius (r2) = 5 m
Lateral height (l) = 5m
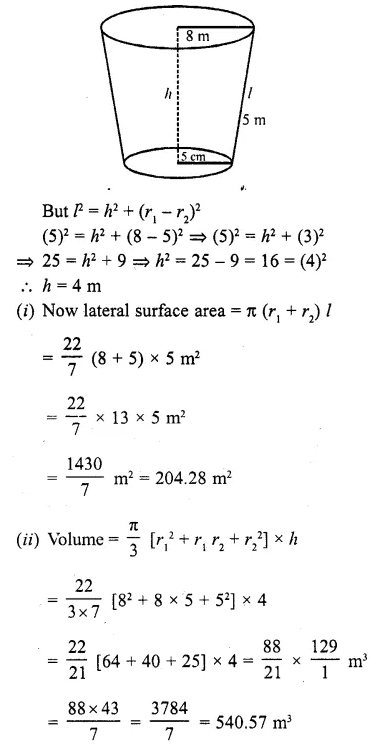
Question 61.
A frustum of a cone is 9 cm thick and the diameters of its circular ends are 28 cm and 4 cm. Find the volume and lateral surface area of the frustum. (Take π = 22/7)
Solution:
Upper diameter = 28 cm
and lower diameter = 4 cm
Height (h) = 9 cm

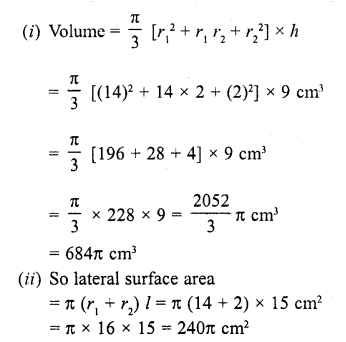
Question 62.
A bucket is in the form of a frustum of a cone and holds 15.25 litres of water. The diameters of the top and bottom are 25 cm and 20 cm respectively. Find its height and area of tin used in its construction.
Solution:
Water in a bucket (frustum) = 15.25l
Upper diameter = 25 cm
and lower diameter = 20 cm
∴ Upper radius (r1) = \((\frac { 25 }{ 2 } )\) cm
and lower radius (r2) = \((\frac { 20 }{ 2 } )\) cm =10 cm
Volume = 15.25 /= 1525 x 10 cm³ = 15250 cm³
Let h be its height

Question 63.
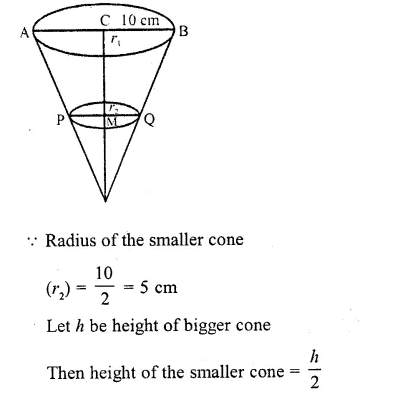
If a cone of radius 10 cm is divided into two parts by drawing a plane through the mid-point of its axis, parallel to its base. Compare the volumes of the two parts. (C.B.S.E. 2000C)
Solution:
Radius of the cone (r1) = 10 cm
Cone is divided into 2 parts Such that PQ || AB

Question 64.
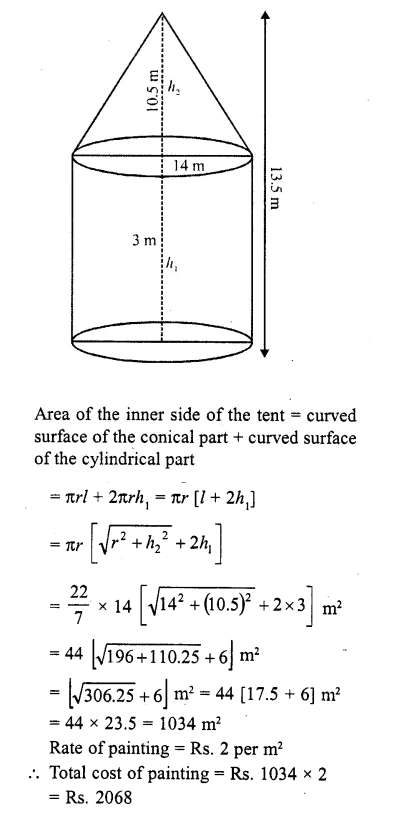
A tent is of the shape of a right circular cylinder upto a height of 3 metres and then becomes a right circular cone with a maximum height of 13.5 pnetres above the ground. Calculate the cost of painting the inner side of the tent at the rate of Rs. 2 per square metre, if the radius of the base is 14 metres
Solution:
Radius of the cylinder (r) = 14 m
and total height of the tent = 13.5 m
Height of the cylindrical part (h1) = 3 m
Height of conical part (h2) = 13.5-3.0 = 10.5m
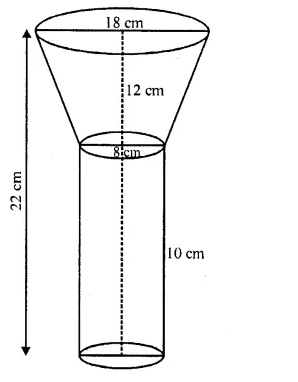
Question 65.
An oil funnel of tin sheet consists of a cylindrical portion 10 cm long attached to a frustum of a cone. If the total height be 22 cm, the diameter of the cylindrical portion 8 cm and the diameter of the top of the funnel 18 cm, find the area of the tin required. (Use : π = 22/7).
Solution:
Upper diameter of the frustum = 18 cm
and lower diameter = 8m

Question 66.
A solid cylinder of diameter 12 cm and height 15 cm is melted and recast into toys with the shape of a right circular cone mounted on a hemisphere of radius 3 cm. If the height of the toy is 12 cm, find the number of toys so formed. (C.B.S.E. 2006C)
Solution:
Diameter of solid cylinder = 12 cm
and height (h1) = 15 cm
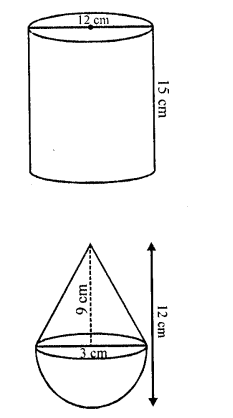

Question 67.
A container open at the top, is in the form of a frustum of a cone of height 24 cm with radii of its lower and upper circular ends as 8 cm and 20 cm respectively. Find the cost of milk which can completely fill the container at the rate of ₹21 per litre. (Use π = 22/7)
Solution:
Upper radius (R) = 20 cm
Lower radius (r) = 8 cm
Height (h) = 24 cm

Question 68.
A cone of maximum size is carved out from a cube of edge 14 cm. Find the . surface area of the cone and of the remaining solid left out after the cone carved out. [NCERT Exemplar]
Solution:
The cone of maximum size that is carved out from a cube of edge 14 cm will be of base radius 7 cm and the height 14 cm.
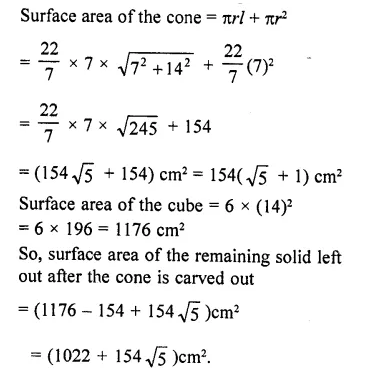
Question 69.
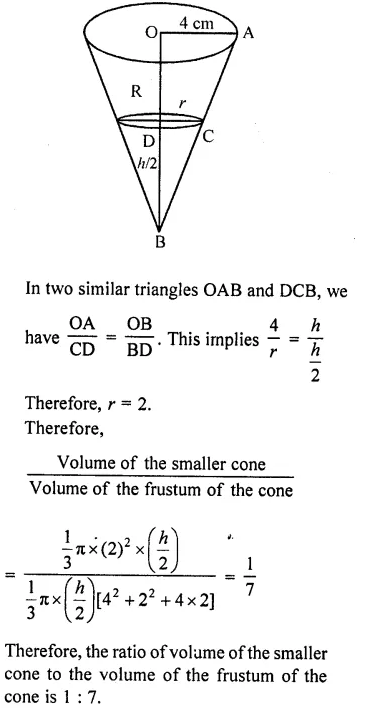
A cone of radius 4 cm is divided into two parts by drawing a plane through the mid point of its axis and parallel to its base. Compare the volumes of two parts. [NCERT Exemplar]
Solution:
Let h be the height of the given cone. One dividing the cone through the mid-point of its axis and parallel to its base into two parts, we obtain the following figure:
Question 70.
A wall 24 m, 0.4 m thick and 6 m high is constructed with the bricks each of dimensions 25 cm x 16 cm x 10 cm. If the mortar occupies \((\frac { 1 }{ 10 } )\) th of the volume of the wall, then find the number of bricks used in constructing the wall. [NCERT Exemplar]
Solution:
Given that, a wall is constructed with the help of bricks and mortar.
∴ Number of bricks


Question 71.
A bucket is in the form of a frustum of a cone and holds 28.490 litres of water. The radii of the top and bottom are 28 cm and 21 cm respectively. Find the height of the bucket. [NCERT Exemplar]
Solution:

Question 72.
Marbles of diameter 1.4 cm are dropped into a cylindrical beaker of diameter 7 cm containing some water. Find the number of marbles that should be dropped into the beaker so that the water level rises by 5.6 cm. [NCERT Exemplar]
Solution:

Question 73.
Two cones with same base radius 8 cm and height 15 cm are joined together along their bases. Find the surface area of the shape formed. [NCERT Exemplar]
Solution:
If two cones with same base and height are joined together along their bases, then the shape so formed is look like as figure shown.

Question 74.
From a solid cube of side 7 cm, a conical cavity of height 7 cm and radius 3 cm is hollowed out. Find the volume of the remaining solid. [NCERT Exemplar]
Solution:
Given that, side of a solid cube (a) = 1 cm
Height of conical cavity i.e., cone, h = 7 cm
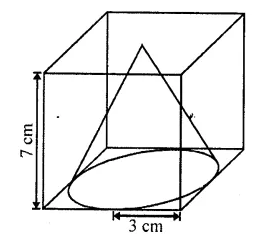
Since, the height of conical cavity and the side of cube is equal that means the conical cavity fit vertically in the cube.
Radius of conical cavity i. e., cone, r = 3 cm
⇒ Diameter = 2 x r = 2 x 3 = 6 cm
Since, the diameter is less than the side of a cube that means the base of a conical cavity is not fit inhorizontal face of cube.
Now, volume of cube = (side)³ = a³ = (7)³ = 34³ cm³
and volume of conical cavity i.e., cone
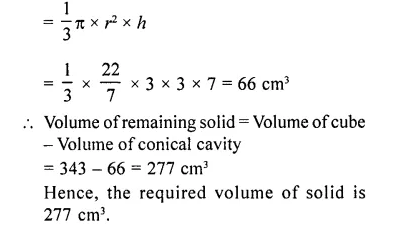
Question 75.
Two solid cones A and B are placed in a cylindrical tube as shown in the figure. The ratio of their capacitites are 2 : 1. Find the heights and capacities of the cones. Also, find the volume of the remaining portion of the cylinder. [NCERT Exemplar]
Solution:


Question 76.
An icecream cone full of icecream having radius 5 cm and height 10 cm as shown’in the figure. Calculate the volume of icecream, provided that its 1/6 parts is left unfilled with icecream.
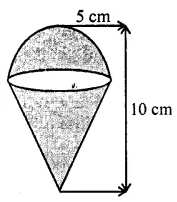
Solution:
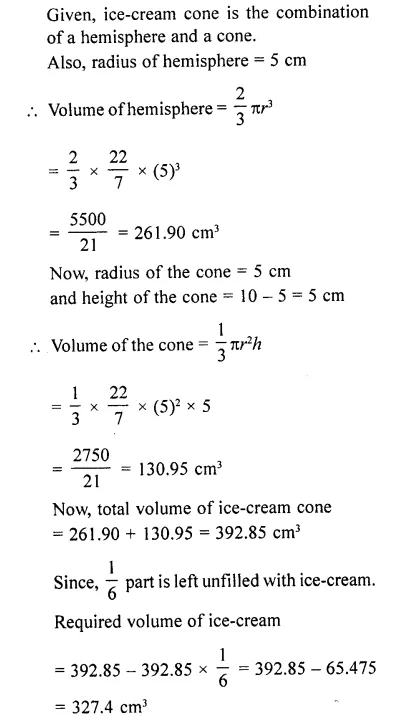
Hope given RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.