Check the below NCERT MCQ Questions for Class 11 Maths Chapter 1 Sets with Answers Pdf free download. MCQ Questions for Class 11 Maths with Answers were prepared based on the latest exam pattern. We have provided Sets Class 11 Maths MCQs Questions with Answers to help students understand the concept very well.
MCQ Questions for Class 11 Hindi with Answers were prepared based on the latest exam pattern.
Class 11 Maths Chapter 1 MCQ With Answers
Maths Class 11 Chapter 1 MCQs On Sets
Question 1.
If A, B and C are any three sets, then A – (B ∪ C) is equal to
(a) (A – B) ∪ (A – C)
(b) (A – B) ∪ C
(c) (A – B) ∩ C
(d) (A – B) ∩ (A – C)
Answer
Answer: (d) (A – B) ∩ (A – C)
Hint:
Given A, B and C are any three sets.
Now, A – (B ∪ C) = (A – B) ∩ (A – C)
Question 2.
(A’)’ = ?
(a) ∪ – A
(b) A’
(c) ∪
(d) A
Answer
Answer: (d) A
Hint:
(A’)’ = A
Question 3.
A – B is read as?
(a) Difference of A and B of B and A
(b) None of the above
(c) Difference of B and A
(d) Both a and b
Answer
Answer: (a) Difference of A and B of B and A
Hint:
A – B will read as difference of A and B of B and A
Ex: Let A = {1, 2, 3, 4, 5} and B = {1, 3, 5, 7}
Now, A – B = {2, 4}
Question 4.
If A, B and C are any three sets, then A × (B ∪ C) is equal to
(a) (A × B) ∪ (A × C)
(b) (A ∪ B) × (A ∪ C)
(c) None of these
(d) (A × B) ∩ (A × C)
Answer
Answer: (a) (A × B) ∪ (A × C)
Hint:
Given A, B and C are any three sets.
Now, A × (B ∪ C) = (A × B) ∪ (A × C)
Question 5.
IF A = [5, 6, 7] and B = [7, 8, 9] then A ∪ B is equal to
(a) [5, 6, 7, 8, 9]
(b) [5, 6, 7]
(c) [7, 8, 9]
(d) None of these
Answer
Answer: (a) [5, 6, 7, 8, 9]
Hint:
Given A = [5, 6, 7] and B = [7, 8, 9]
then A ∪ B = [5, 6, 7, 8, 9]
Question 6.
Which of the following sets are null sets
(a) {x: |x |< -4, x ?N}
(b) 2 and 3
(c) Set of all prime numbers between 15 and 19
(d) {x: x < 5, x > 6}
Answer
Answer: (b) 2 and 3
Hint:
2 and 3 is the null set.
Question 7.
IF R = {(2, 1),(4, 3),(4, 5)}, then range of the function is?
(a) Range R = {2, 4}
(b) Range R = {1, 3, 5}
(c) Range R = {2, 3, 4, 5}
(d) Range R {1, 1, 4, 5}
Answer
Answer: (b) Range R = {1, 3, 5}
Hint:
Given R = {(2, 1),(4, 3),(4, 5)}
then Range(R) = {1, 3, 5}
Question 8.
The members of the set S = {x | x is the square of an integer and x < 100} is
(a) {0, 2, 4, 5, 9, 58, 49, 56, 99, 12}
(b) {0, 1, 4, 9, 16, 25, 36, 49, 64, 81}
(c) {1, 4, 9, 16, 25, 36, 64, 81, 85, 99}
(d) {0, 1, 4, 9, 16, 25, 36, 49, 64, 121}
Answer
Answer: (b) {0, 1, 4, 9, 16, 25, 36, 49, 64, 81}
Hint:
The set S consists of the square of an integer less than 100
So, S = {0, 1, 4, 9, 16, 25, 36, 49, 64, 81}
Question 9.
In a class of 120 students numbered 1 to 120, all even numbered students opt for Physics, whose numbers are divisible by 5 opt for Chemistry and those whose numbers are divisible by 7 opt for Math. How many opt for none of the three subjects?
(a) 19
(b) 41
(c) 21
(d) 57
Answer
Answer: (b) 41
Hint:
The number of students who took at least one of the three subjects can be found by finding out A ∪ B ∪ C, where A is the set of those who took Physics, B the set of those who took Chemistry and C the set of those who opted for Math.
Now, A ∪ B ∪ C = A + B + C – (A ∩ B + B ∩ C + C ∩ A) + (A ∩ B ∩ C)
A is the set of those who opted for Physics = 120/2 = 60 students
B is the set of those who opted for Chemistry = 120/5 = 24
C is the set of those who opted for Math = 120/7 = 17
The 10th, 20th, 30th….. numbered students would have opted for both Physics and Chemistry.
Therefore, A ∩ B = 120/10 = 12
The 14th, 28th, 42nd….. Numbered students would have opted for Physics and Math.
Therefore, C ∩ A = 120/14 = 8
The 35th, 70th…. numbered students would have opted for Chemistry and Math.
Therefore, B ∩ C = 120/35 = 3
And the 70th numbered student would have opted for all three subjects.
Therefore, A ∪ B ∪ C = 60 + 24 + 17 – (12 + 8 + 3) + 1 = 79
Number of students who opted for none of the three subjects = 120 – 79 = 41
Question 10.
{ (A, B) : A² +B² = 1} on the sets has the following relation
(a) reflexive
(b) symmetric
(c) none
(d) reflexive and transitive
Answer
Answer: (b) symmetric
Hint:
Given {(a, b) : a² + b² = 1} on the set S.
Now a² +b² = b² + a² = 1
So, the given relation is symmetric.
Question 11.
Two finite sets have N and M elements. The number of elements in the power set of first set is 48 more than the total number of elements in power set of the second test. Then the value of M and N are
(a) 7, 6
(b) 6, 4
(c) 7, 4
(d) 6, 3
Answer
Answer: (b) 6, 4
Hint:
Let A and B be two sets having m and n numbers of elements respectively
Number of subsets of A = 2m
Number of subsets of B = 2n
Now, according to question
2m – 2n = 48
⇒ 2n(2m – n – 1) = 24(22 – 1)
So, n = 4
and m – n = 2
⇒ m – 4 = 2
⇒ m = 2 + 4
⇒ m = 6
Question 12.
The range of the function f(x) = 3x – 2‚ is
(a) (- ∞, ∞)
(b) R – {3}
(c) (- ∞, 0)
(d) (0, – ∞)
Answer
Answer: (a) (- ∞, ∞)
Hint:
Let the given function is
y = 3x – 2
⇒ y + 2 = 3x
⇒ x = (y + 2)/3
Now x is saisfied by all values.
So, Range{f(x)} = R = (-∞, ∞)
Question 13.
If A, B, C be three sets such that A ∪ B = A ∪ C and A ∩ B = A ∩ C, then,
(a) B = C
(b) A = C
(c) A = B = C
(d) A = B
Answer
Answer: (a) B = C
Hint:
Given A, B, C be three sets such that A ∪ B = A ∪ C and A ∩ B = A ∩ C then B = C
Question 14.
In 2nd quadrant?
(a) X < 0, Y < 0
(b) X < 0, Y > 0
(c) X > 0, Y > 0
(d) X > 0, Y < 0
Answer
Answer: (b) X < 0, Y > 0
Hint:
In the second quadrant,
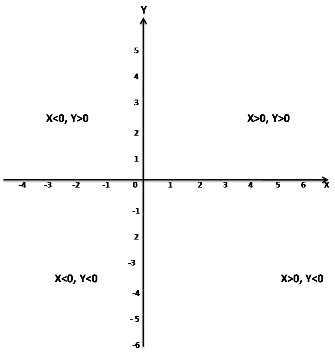
X < 0, Y > 0
Question 15.
How many rational and irrational numbers are possible between 0 and 1?
(a) 0
(b) Finite
(c) Infinite
(d) 1
Answer
Answer: (c) Infinite
Hint:
There are infinite many rational and irrational numbers are possible between 0 and 1
This is because between any two numbers, there are infinite numbers.
Question 16.
Empty set is a?
(a) Finite Set
(b) Invalid Set
(c) None of the above
(d) Infinite Set
Answer
Answer: (a) Finite Set
Hint:
In mathematics, and more specifically set theory, the empty set is the unique set having no elements and its size or cardinality (count of elements in a set) is zero.
So, an empty set is a finite set.
Question 17.
If A = [5, 6, 7] and B = [7, 8, 9] then A U B is equal to
(a) [5, 6, 7, 8, 9]
(b) [5, 6, 7]
(c) [7, 8, 9]
(d) None of these
Answer
Answer: (a) [5, 6, 7, 8, 9]
Hint:
Given A = [5, 6, 7] and B = [7, 8, 9]
then A U B = [5, 6, 7, 8, 9]
Question 18.
Which of the following two sets are equal?
(a) A = {1, 2} and B = {1}
(b) A = {1, 2} and B = {1, 2, 3}
(c) A = {1, 2, 3} and B = {2, 1, 3}
(d) A = {1, 2, 4} and B = {1, 2, 3}
Answer
Answer: (c) A = {1, 2, 3} and B = {2, 1, 3}
Hint:
Two sets are equal if and only if they have the same elements.
So, A = {1, 2, 3} and B = {2, 1, 3} are equal sets.
Question 19.
In a class of 50 students, 10 did not opt for math, 15 did not opt for science and 2 did not opt for either. How many students of the class opted for both math and science.
(a) 24
(b) 25
(c) 26
(d) 27
Answer
Answer: (d) 27
Hint:
Total students = 50
Students who did not opt for math = 10
Students who did not opt for Science = 15
Students who did not opt for either maths or science = 2
Total of 40 students in math and 13 did not opt for science but did for math = 40 – 13 = 27
So, students of the class opted for both math and science is 27
Question 20.
In last quadrant?
(a) X < 0, Y > 0
(b) X < 0, Y < 0
(c) X > 0, Y < 0
(d) X > 0, Y > 0
Answer
Answer: (d) X > 0, Y > 0
Hint:
In the last quadrant,
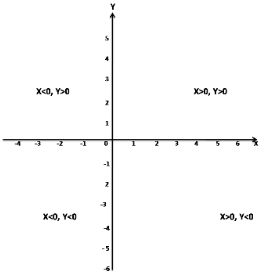
X > 0, Y > 0
We hope the given NCERT MCQ Questions for Class 11 Maths Chapter 1 Sets with Answers Pdf free download will help you. If you have any queries regarding CBSE Class 11 Maths Sets MCQs Multiple Choice Questions with Answers, drop a comment below and we will get back to you soon.
Class 10 Maths MCQ:
- Sets Class 11 MCQ
- Relations and Functions Class 11 MCQ
- Trigonometric Functions Class 11 MCQ
- Principle of Mathematical Induction Class 11 MCQ
- Complex Numbers and Quadratic Equations Class 11 MCQ
- Linear Inequalities Class 11 MCQ
- Permutations and Combinations Class 11 MCQ
- Binomial Theorem Class 11 MCQ
- Sequences and Series Class 11 MCQ
- Straight Lines Class 11 MCQ
- Conic Sections Class 11 MCQ
- Introduction to Three Dimensional Geometry Class 11 MCQ
- Limits and Derivatives Class 11 MCQ
- Mathematical Reasoning Class 11 MCQ
- Statistics Class 11 MCQ
- Probability Class 11 MCQ