Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems (Based on Quadratic Equations) Ex 6C
These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6C.
Other Exercises
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6A
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6B
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6C
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6D
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6E
Question 1.
The speed of an ordinary train is x km/hr and that of an express train is (x + 25) km per hour.
(i) Find the time taken by each train to cover 300 km.
(ii) If the ordinary train takes 2 hrs more than the express train; calculate speed of the express train.
Solution:
Speed of an ordinary train = x km/ hr
and speed of an express train = (x + 25) km/hr.
(i) Time taken by ordinary train to cover 300 km = \(\frac { 300 }{ x }\) hr
(ii) Time taken by express train to cover 300 km = \(\frac { 300 }{ x + 25 }\) hr
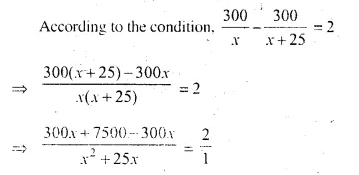
⇒ 7500 = 2x² + 50x
⇒ 2x² + 50x – 7500 = 0
⇒ x² + 25x – 3750 = 0 (Dividing by 2)
⇒ x² + 75x – 50x – 3750 = 0
⇒ x (x + 75) -50 (x + 75) = 0
⇒ (x + 75) (x – 50) = 0
Either x + 75 = 0 then x = -75 But it is not possible,
or x – 50 = 0 then x = 50
Speed of an ordinary train = 50 km/ hr
and speed of express train = 50 + 25 = 75 km/ hr
Question 2.
If the speed of a car is increased by 10 km per hr, it takes 18 minutes less to cover a distance of 36 km. Find the speed of the car.
Solution:
Let the speed of ear = x km/hr
time taken to cover 36 km = \(\frac { 36 }{ x }\) hr
In second case,
Speed of car = (x + 10) km/hr
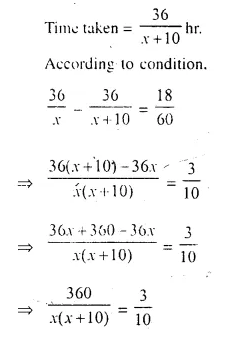
⇒ 3x² + 30 x = 3600
⇒ 3x² + 30x – 3600 = 0 .
⇒ x² + 10x – 1200 = 0 (Dividing by 3)
⇒ x² + 40x – 30x – 1200 = 0
⇒ x (x + 40) – 30 (x + 40) = 0
⇒ (x + 40) (x – 30) = 0
Either x + 40 = 0 then x = – 40 But it is not possible,
or x – 30 = 0, then x = 30
Speed of car = 30 km/hr.
Question 3.
If the speed of an aeroplane is reduced by 40 km/per hr, it takes 20 minutes more to cover 1200 km. Find the speed of the aeroplane.
Solution:
Let the speed of aeroplane = x km/hr.

⇒ x² – 40x = 144000
⇒ x² – 40x – 144000 = 0
⇒ x² – 400x + 360x – 144000 = 0
⇒ x (x – 400) + 360 (x – 400) = 0
Either x – 400 = 0, then x = 400
or x + 360 = 0, then x = – 360, But it is not possible.
x = 400
Hence speed of aeroplane = 400 km/hr.
Question 4.
A car covers a distance of 400 km at a certain speed. Had the speed been 12 km/h more, the time taken for the journey would have been 1 hour 40 minutes less. Find the original speed of the car.
Solution:
Let the original speed of the car be x km/h.

⇒ 1200x + 14400 – 1200x = 5x² + 60x
⇒ 14400 = 5x² + 60x
⇒ x² + 12x – 2880 = 0 (Dividing by 5)
⇒ x² + 60x – 48x – 2880 = 0
⇒ x (x + 60) – 48 (x + 60) = 0
⇒ (x + 60) (x – 48) = 0
⇒ x = 48 or x = -60
⇒ x = 48 (Rejecting x = -60, being speed)
Hence, original speed of the car = 48 km/h.
Question 5.
A girl goes to her friend’s house, which is at a distance of 12 km. She covers half of the distance at a speed of ‘x’ km/hr. and the remaining distance at a speed of (x + 2) km/hr. If she takes 2 hrs. 30 minutes to cover the whole distance; find ‘x’
Solution:
Distance = 12 km.
Speed for the first half distance = x km/hr.
and for the second half distance = (x + 2) km/hr.
Total time taken = 2 hrs. 30 minutes.
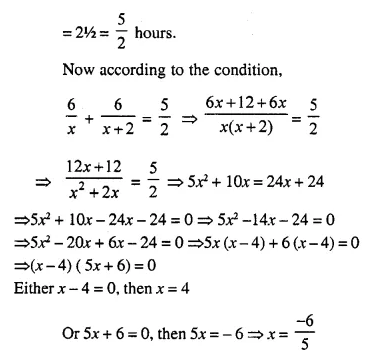
But it is not possible.
Speed for first half distance (x) = 4 km/hr
Question 6.
A car made a run of 390 km in ‘x’ hours. If the speed had been 4 km per hour more, it would have taken 2 hours less for the journey. Find ‘x’.
Solution:
Distance = 390 km
time = x hours
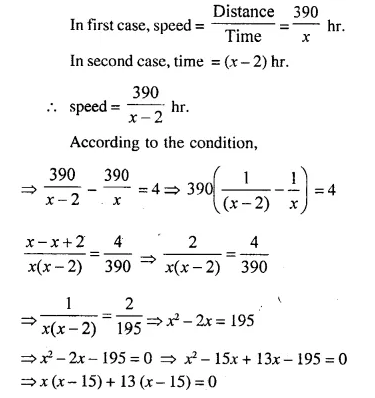
⇒ (x – 15) (x + 13) = 0
Either x – 15 = 0, then x = 15
or (x + 13) = 0 then x = -13 Which is not possible.
Value of x = 15
Question 7.
A goods train leaves a station at 6 p.m., followed by an express train which leaves at 8 p.m. and travels 20 km/hour faster than the goods train. The express train arrives at a station, 1040 km away, 36 minutes before the goods train. Assuming that the speeds of both the trains remain constant between the two stations; calculate their speeds.
Solution:
Departure of goods train = 6 p.m.
and departure of express train = 8 p.m.
Speed of express train is more than goods trains by 20 km/hr
Total distance = 1040 km
Let speed of goods train = x km/hr
Then speed of express train = (x + 20) km/hr
Difference of time taken = 8 p.m. – 6 p.m. + 36 minutes = 2 hours 36 minutes
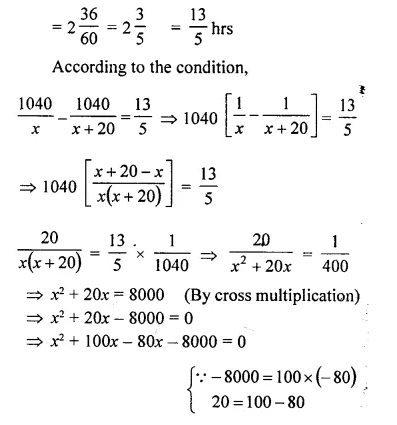
⇒ x – (x + 100) – 80 (x + 100) = 0
⇒ (x + 100) (x – 80) = 0
Either x + 100 = 0, then x = -100 but it is not possible being negative
or x – 80 = 0, then x = 80
Speed of goods train = 80 km/hr
and speed of express train = 80 + 20 = 100 km/hr
⇒ 13x² + 507x – 35100 = 0
⇒ x² + 39x – 2700 = 0 (Dividing by 13)
⇒ x² + 75x – 36x – 2700 = 0
⇒ x (x + 75) – 36(x + 75) = 0
⇒ (x + 75) (x – 36) = 0
Either x + 75 = 0, then x = – 75 Which is not possible,
or x – 36 = 0 then x = 36
Speed of goods train = 36 km/hr
and speed of express train = 36 + 39 = 75 km/hr.
Question 8.
A man bought an article for Rs. x and sold it for Rs. 16. If his loss was x percent, find the cost price of the article.
Solution:
C.P. of article = Rs. x
S.R = Rs. 16
Loss = C.P. – S.P. = Rs. (x – 16)
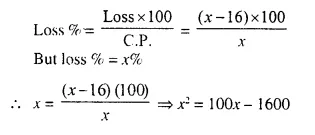
⇒ x² – 100x + 1600 = 0
⇒ x² – 20x – 80x + 1600 = 0
⇒ x (x – 20) – 80 (x – 20) = 0
⇒ (x – 20) (x – 80) = 0
Either x – 20 = 0, then x = 20
or x – 80 = 0, then x = 80
Cost Price = Rs. 20 or Rs. 80
Question 9.
A trader bought an article for Rs. x and sold it for Rs. 52, thereby making a profit of (x – 10) per cent on his outlay. Calculate the cost price.
Solution:
Let C.P. = Rs. x
S.R = Rs. 52
Profit = S.P – C.P. = Rs. 52 – x

x² – 10x = 5200 – 100x
⇒ x² – 10x + 100x – 5200 = 0
⇒ x² + 90x – 5200 = 0
⇒ x2 + 130x – 40x – 5200 = 0
⇒ x (x + 130) – 40(x + 130) = 0
⇒ (x + 130) (x – 40 ) = 0
Either x + 130 = 0 , then x = – 130 which is not possible.
or x – 40 = 0 then x = 40
Cost price = Rs. 40
Question 10.
By selling a chair for Rs. 75, Mohan gained as much per cent as its cost. Calculate the cost of the chair.
Solution:
Let. C.P of chair = Rs. x
Profit = x %
S.P. = Rs. 75
Total profit = Rs. (75 – x)
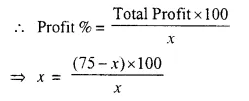
⇒ x² = 7500 – 100x
⇒ x² + 100x – 7500 = 0
⇒ x²+ 150x – 50 – 7500 = 0
⇒ x (x + 150) – 50 (x + 150) = 0
⇒ (x + 150) (x – 50) = 0
Either x + 150 = 0, then x = -150 which is not possible
or x – 50 = 0, Then x = 50
Cost price of chair = Rs. 50
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6C are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.