Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems (Based on Quadratic Equations) Ex 6A
These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6A.
Other Exercises
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6A
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6B
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6C
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6D
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6E
Question 1.
The product of two consecutive integers is 56. Find the integers.
Solution:
Let the first integer = x
Then second integer = x + 1
Now according to the condition given
x (x + 1) = 56
⇒ x² + x – 56 = 0
⇒ x² + 8x – 7x – 56 = 0
⇒ x (x + 8) – 7 (x + 8) = 0
⇒ (x + 8) (x – 7) = 0
Either x + 8 = 0, then x = – 8
or x – 7 = 0, then x = 7
(i) If x = -8, then
first integer = -8
and second integer = – 8 + 1 = – 7
(ii) If x = 7, then
first integer = 7
and second integer = 7 + 1 = 8
Integers are 7, 8 or -8, -7
Question 2.
The sum of the squares of two consecutive natural numbers is 41. Find the numbers.
Solution:
Let the first natural number = x
Then second natural number = x + 1
Now according to the condition given,
(x)² + (x + 1)² = 41
⇒ x² + x² + 2x + 1 = 41
⇒ 2x² + 2x + 1 – 41 = 0
⇒ 2x² + 2x – 40 = 0
⇒ x² + x – 20 = 0 (Dividing by 2)
⇒ x² + 5x – 4x – 20 = 0
⇒ x (x + 5) – 4 (x + 5) = 0
⇒ (x + 5) (x – 4) = 0
Either x + 5 = 0 then x = – 5 But it is not a natural number
or x – 4 = 0, Then x = 4
Numbers are 4 and 5
Question 3.
Find the two natural numbers which differ by 5 and the sum of whose squares is 97.
Solution:
Let the first natural number = x
Then second natural number = x + 5
Now according to the given condition,
(x)² + (x + 5)² = 97
⇒ x² + x² + 10x + 25 – 97 = 0
⇒ 2x² + 10x – 72 = 0
⇒ x² + 5x – 36 = 0 (Dividing by 2)
⇒ x² + 9x – 4x – 36 = 0
⇒ x (x + 9) – 4 (x + 9) = 0
⇒ (x + 9) (x – 4) = 0
Either x + 9 = 0, then x = – 9 But it is not a natural number
or x – 4 = 0, then x = 4
First number = 4
and second number = 4 + 5 = 9
Question 4.
The sum of a number and its reciprocal is 4.25. Find the number.
Solution:
Let the number = x
Now according to the condition,
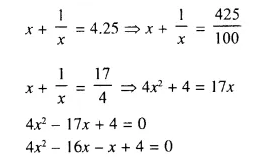
⇒ 4x (x – 4) – 1 (x – 4) = 0
⇒ (x – 4) (4x – 1) = 0
Either x – 4 = 0, then x = 4
or 4x – 1 = 0, 4x = 1 then x = \(\frac { 1 }{ 4 }\)
Number is 4 or \(\frac { 1 }{ 4 }\)
Question 5.
Two natural numbers differ by 3. Find the numbers, if the sum of their reciprocals is \(\frac { 7 }{ 10 }\)
Solution:
Let the first natural number = x
Then second natural number = x + 3
Now according to the given condition,
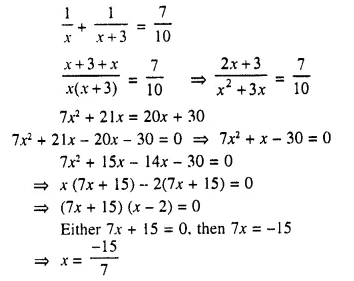
But it is not a natural number
or x – 2 = 0, then x = 2
First number = 2
and second number = 2 + 3 = 5
Question 6.
Divide 15 into two parts such that the sum of their reciprocals is \(\frac { 3 }{ 10 }\).
Solution:
Let first part = x
Then second part = 15 – x (sum = 15)
Now according to the given condition,
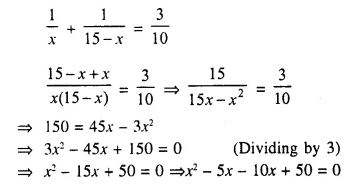
⇒ x (x – 5) – 10 (x – 5) = 0
⇒ (x – 5) (x – 10) = 0
Either x – 5 = 0, then x = 5
or x – 10 = 0, then x = 10
If x = 5, then first part = 15 – 5 = 10
If x = 10, then second part = 15 – 10 = 5
Parts are 5, 10
Question 7.
The sum of the squares of two positive integers is 208. If the square of the larger number is 18 times the smaller number, find the numbers.
Solution:
Let x be the larger number and y be the smaller number, then
According to the conditions x2 = 18 ….(i)
and x² + y² = 208 ….(ii)
⇒ 18y + y² = 208 [From (i)]
⇒ y² + 18y – 208 = 0
⇒ y² + 26y – 8y – 208 = 0
⇒ y (y + 26) – 8 (y + 26) = 0
⇒ (y + 26) (y – 8) = 0
Either y + 26 = 0, then y = -26
But it is not possible as it is not positive
or y – 8 = 0, then y = 8
Then x² = 18y ⇒ y² = 18 x 8 ⇒x² = 144 = (12)² ⇒ x = 12
Number are 12, 8
Question 8.
The sum of the squares of two consecutive positive even numbers is 52. Find the numbers.
Solution:
Let first even number = 2x
and second even number = 2x + 2
Now according to the given condition,
(2x)² + (2x + 2)² = 52
⇒ 4x² + 4x² + 8x + 4 = 52
⇒ 4x² + 4x² + 8x + 4 – 52 = 0
⇒ 8x² + 8x – 48 = 0
⇒ x² + x – 6 = 0 (Dividing by 8)
⇒ x² + 3x – 2x – 6 = 0
⇒ x (x + 3) – 2 (x + 3) = 0
⇒ (x + 3) (x – 2) = 0
Either x + 3 = 0, then x = – 3 But it is not possible because it is not positive.
or x – 2 = 0, then x = 2
First even number = 2 x 2 = 4
Second number = 4 + 2 = 6
Hence numbers are 4, 6
Question 9.
Find two consecutive positive odd numbers, the sum of whose squares is 74.
Solution:
Let first odd number = 2x -1
Second odd number = 2x – 1 + 2 = 2x + 1
Now according to the given condition,
(2x – 1)² + (2x + 1)² = 74
⇒ 4x² – 4x + 1 + 4x² + 4x + 1 = 74
⇒ 8x² + 2 – 74 = 0
⇒ 8x² – 72 = 0
⇒ x² – 9 = 0 (Dividing by 8)
⇒ (x + 3) (x – 3) = 0
Either x + 3 = 0, then x = -3 But it is not possible because it is not positive.
or x – 3 = 0, then x = 3
First odd number = 2x – 1 = 2 x 3 – 1 = 6 – 1 = 5
and second odd number = 5 + 2 = 7
Number are 5, 7
Question 10.
The denominator of a positive fraction is one more than twice the numerator. If the sum of the fraction and its reciprocal is 2.9; find the fraction.
Solution:
Let numerator of a fraction = x
Then denominator = 2x + 1

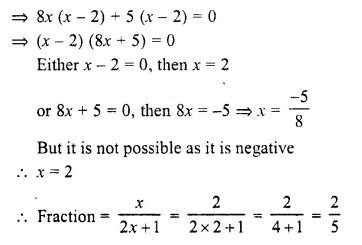
Question 11.
Three positive numbers are in the ratio \(\frac { 1 }{ 2 }\) : \(\frac { 1 }{ 3 }\) : \(\frac { 1 }{ 4 }\) Find the numbers; if the sum of their squares is 244.
Solution:
Multiply each ratio by L.C.M. of de-nominators i.e. by 12.
We get, 6 : 4 : 3
Let first positive number = 6x
Then second number = 4x
and third number = 3x
According to the given condition,
(6x)² + (4x)² + (3x)² = 244
⇒ 36x² + 16x² + 9x² = 244
⇒ 61x² = 244
⇒ x² – 4 = 0
⇒ (x + 2) (x – 2) = 0
Either x + 2 = 0, then x = -2 But it is not possible because it is not positive
or x – 2 = 0, then x = 2
First number = 6x = 6 x 2 = 12
Second number = 4x = 4 x 2 = 8
and third number = 3x = 3 x 2 = 6
Numbers are 12, 8, 6
Question 12.
Divide 20 into two parts such that three times the square of one part exceeds the other part by 10.
Solution:
Let first part = x
Then second part = 20 – x (Sum = 20)
Now, according to the given condition,
3(x)² – (20 – x) = 10
⇒ 3x² – 20 + x – 10 = 0
⇒ 3x² + x – 30 = 0
⇒ 3x² + 10x – 9x – 30 = 0
⇒ x (3x + 10) – 3 (3x + 10) = 0
⇒ (3x + 10) (x – 3) = 0
Either 3x + 10 = 0, then 3x = -10 ⇒ x = \(\frac { -10 }{ 3 }\)
But it is not possible.
or x – 3 = 0 then x = 3
Then first part = 3
and second part = 20 – 3 = 17
Question 13.
Three consecutive natural numbers are such that the square of the middle number exceeds the difference of the squares of the other two by 60. Assume the middle number to be x and form a quadratic equation satisfying the above statement Hence ; find the three numbers.
Solution:
Let middle number = x
Then, first number = x – 1
and third number = x + 1
Now according to the condition,
(x)²= [(x + 1)² – (x – 1)²] + 60
⇒ x² = [x² + 2x + 1 – x² + 2x – 1 ] + 60
⇒ x² = 4x + 60
⇒ x² – 4x – 60 = 0
⇒ x² – 10x + 6x – 60 = 0
⇒ x (x – 10) + 6 (x – 10) = 0
⇒ (x – 10) (x + 6) = 0
Either x – 10 = 0 then x = 10
or x + 6 = 0 then x = -6. But it is not a natural number.
Middle number = 10
First number = 10 – 1 = 9
and third number = 10 + 1 = 11
Hence numbers are 9, 10, 11
Question 14.
Out of three consecutive positive integers, the middle number is p. If three times the square of the largest is greater than the sum of the squares of the other two numbers by 67; calculate the value of p.
Solution:
Middle number = p
then smallest number = p – 1
and greatest number = p + 1
Now, according to the condition.
3 (p + 1)² – (p – 1)² – p² = 67
⇒ 3 (p² + 2p + 1) – (p² – 2p + 1) – p² = 67
⇒ 3p² + 6p + 3 – p² + 2p – 1 – p² – 67 = 0
⇒ p² + 8p + 2 – 67 = 0
⇒ p² + 8p – 65 = 0
⇒ p² + 13p – 5p – 65 = 0
⇒ p (p + 13) – 5 (p + 13) = 0
⇒ (p + 13) (p – 5) = 0
Either p + 13 = 0, then p = -13 But it is not possible.
or p – 5 = 0, then p = 5
p = 5
Question 15.
A can do a piece of work in ‘x’ days and B can do the same work in (x + 16) days. If both working together can do it in 15 days. Calculate ‘x’.
Solution:
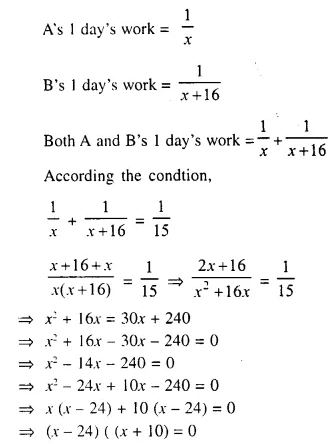
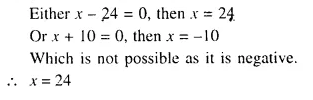
Question 16.
One pipe can fill a cistern in 3 hours less than the other. The two pipes together can fill the cistern in 6 hours 40 minutes. Find the time that each pipe will take to fill the cistern.
Solution:
Let first pipe can fill the cistern in = x hrs.
Second pipe will fill the cistern in = x – 3 hrs.
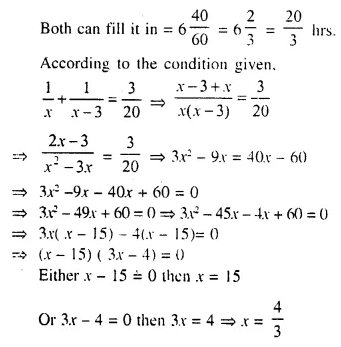
But it is not possible.
x = 15
First pipe can fill in 15 hrs.
and second pipe in 15 – 3 = 12 hrs.
Question 17.
A positive number is divided into two parts such that the sum of the squares of the two parts is 20. The square of the larger part is 8 times the smaller part. Taking A as the smaller part of the two parts. Find the number. (2010)
Solution:
Let larger part = y
and smaller part = x
x² + y² = 20 ….(i)
and y² = 8x ….(ii)
Substituting the value of y² in „
x² + 8x = 20
⇒ x² + 8x – 20 = 0
⇒ x² + 10x – 1x – 20 = 0 {-20 = 10 x (-2), 8 = 10 – 2}
⇒ x (x + 10) – 2(x + 10) = 0
⇒ (x + 10) (x – 2) = 0
Either x + 10 = 0, then x = – 10 which is not possible because it is negative
or x – 2 = 0, then x = 2
Smaller number = 2
and larger number = y² = 8x = 8 x 2 = 16
⇒ y² = 16 = (4)²
⇒ y = 4
Number = x + y = 2 + 4 = 6
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6A are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.