Selina Concise Mathematics Class 10 ICSE Solutions Chapter 18 Tangents and Intersecting Chords Ex 18C
These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 18 Tangents and Intersecting Chords Ex 18C.
Other Exercises
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 18 Tangents and Intersecting Chords Ex 18A
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 18 Tangents and Intersecting Chords Ex 18B
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 18 Tangents and Intersecting Chords Ex 18C
Question 1.
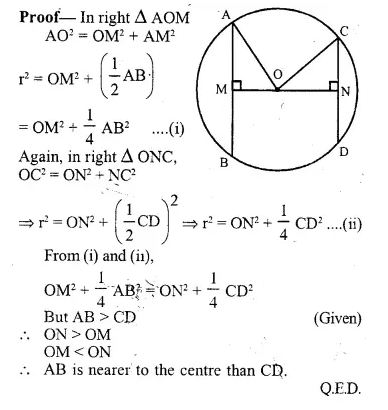
Prove that, of any two chords of a circle, the greater chord is nearer to the centre.
Solution:
Given: In circle with centre O and radius r.
OM ⊥ AB and ON ⊥ CD and AB > CD
To Prove: OM < ON
Construction: Join OA, OC
Question 2.
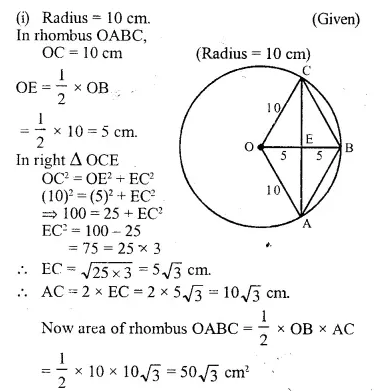
OABC is a rhombus whose three vertices A, B and C lie on a circle with centre O.
(i) If the radius of the circle is 10 cm, find the area of the rhombus.
(ii) If the area of the rhombus is 32√3 cm² find the radius of the circle.
Solution:

Question 3.
Two circles with centres A and B, and radii 5 cm and 3 cm, touch each other internally. If the perpendicular bisector of the segment AB meets the bigger circle in P and Q; find the length of PQ.
Solution:
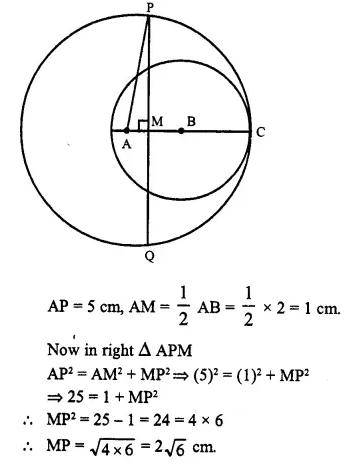
![]()
Two circles with centres A and B touch each other at C internally.
PQ is the perpendicular bisector of AB meeting the bigger circles at P and Q. Join AP.
Radius AC = 5 cm.
and radius BC = 3 cm.
AB = AC – BC = 5-3 = 2 cm.
Question 4.
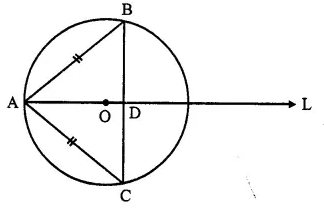
Two chords AB and AC of a circle are equal. Prove that the centre of the circle, lies on the bisector of angle BAC.
Solution:
Given: A circle in which two chords AC and AB are equal in length. AL is the bisector of ∠ BAC.
To Prove: O lies on the bisector of ∠ BAC
Proof: In ∆ ADC and ∆ ADB,
AD = AD (Common)
AB = AC (Given)
∠ BAD = ∠ CAD (Given)
∴ ∆ ADC = ∆ ADB (SAS postulate)
∴ BD = DC (C.P.C.T.)
and ∠ ADB = ∠ ADC (C.P.C.T.)
But ∠ ADB + ∠ ADC = 180° (Linear pair)
∴ ∠ ADB = ∠ ADC = 90°
∴ AD is the perpendicular bisector of chord BC.
∵ The perpendicular bisector of a chord passes through the centre of the circle.
∴ AD is the bisector of ∠ BAC passes through the centre O of the circle. Q.E.D.
Question 5.
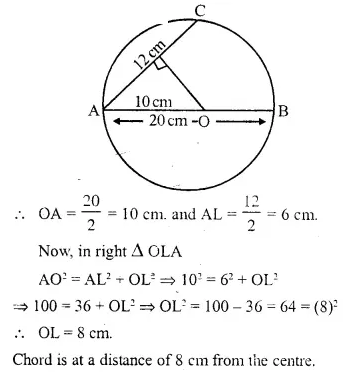
The diameter and a chord of circle have a common end-point. If the length of the diameter is 20 cm and the length of the chord is 12 cm, how far is the chord from the centre of the circle ?
Solution:
AB is the diameter and AC is the chord
∴ AB = 20 cm and AC = 12 cm
Draw OL ⊥ AC
∵ OL ⊥ AC and hence it bisects AC, O is the center of the circle.
Question 6.
ABCD is a cyclic quadrilateral in which BC is parallel to AD, angle ADC = 110° and angle BAC = 50°. Find angle DAC and angle DCA.
Solution:
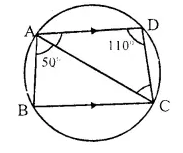
ABCD is a cyclic quad, in which AD || BC
∠ ADC = 110°, ∠ BAC = 50°
∠B + ∠D= 180° (Sum of opposite angles of a cyclic quad.)
⇒∠B + 110°= 180°
∴ ∠ B or ∠ ABC = 180° – 110° – 70″
Now. in ∆ ABC,
∠ BAC + ∠ ABC – ∠ ACB = 180°
⇒ 50° + 70° + ∠ ACB – 180°
⇒ 120° – ∠ ACB = 180°
∴ ∠ ACB = 180° – 120° = 60″
OL ⊥ AC and hence it bisects AC, O is the center of the circle.
OL ⊥ AC and hence it bisects AC, O is the center of the circle.
∵ AD || BC (Given)
∴ ∠ DAC = ∠ ACB (Alternate angles)
= 60°
Now, in ∆ ADC,
∠ DAC + ∠ ADC + ∠ DCA -= 180°
60°+ 110° + ∠ DCA = 180°
170° + ∠ DCA – 180°
∴ ∠ DCA = 180″ – 170° = 10°
Question 7.
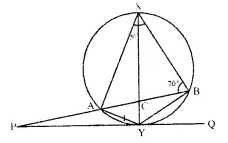
In the given figure, C and D arc points on the semi-circle described on AB as diameter. Given angle BAD = 70° and angle DBC = 30°. calculate angle BDC.
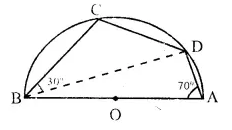
Solution:
∴ ABCD is a cyclic quad.
∠ BAD ∠ BCD 180 (Sum of opposite angles)
⇒ 70° + ∠ BCD = 180°
⇒ ∠ BCD = 180°- 70° = 110°
Now in ∆ BCD,
∠ BCD + ∠ DBC + ∠ BDC = 180°
⇒ 30°+ 110° + ∠ BDC = 180°
⇒ 140°+ ∠ BDC = 180°
∴ ∠ BDC = 180°- 140° = 40°
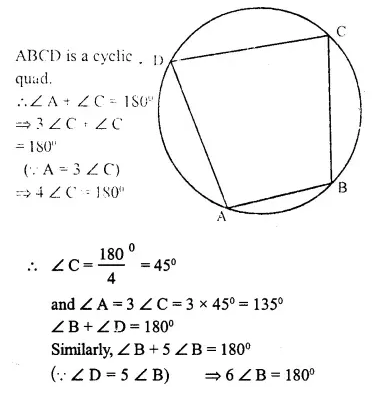
Question 8.
In cyclic quadrilateral ABCD, ∠ A = 3 ∠ C and ∠ D = 5 ∠ B. Find the measure of each angle of the quadrilateral.
Solution:
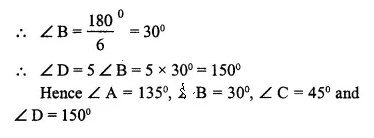
Question 9.
Show that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
Solution:
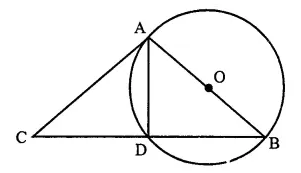
Given: ∆ABC in which AB=AC and AB as diameter, a circle is drawn which intersects BC at D.
To Prove: BD = DC
Construction: Join AD
Proof: AB is the diameter
∴ ∠ ADB = 90° (Angle in a semi-circle)
But ∠ ADB + ∠ ADC =180° (A linear pair)
∴ ∠ ADC = 90°
Now in right angled ∆s ABD and ACD,
Hypotenuse AB = AC (given)
Side AD = AD (Common)
∴ ∆ ABD ≅ ∆ ACD (RHS postulate)
BD = DC (C.P.C.T.)
Hence the circle bisects base BC at D. Q.ED.
Question 10.
Bisectors of vertex angles A, B and C of a triangle ABC intersect its circumcircle at the points D, E and F respectively. Prove that.
angle EDF = 90° – \(\frac { 1 }{ 2 }\)∠A.
Solution:
Given: A ∆ ABC whose bisectors of angles A, B and C intersect the circumcircle at D, E and F respectively. ED, EF and DF are joined.
∠ EDF = 90° – \(\frac { 1 }{ 2 }\)∠A
Construction: Join BF, FA, AE and EC.
Proof: ∠ EBF = ∠ ECF = ∠ EDF ……..(i)
(Angles in the same segment)
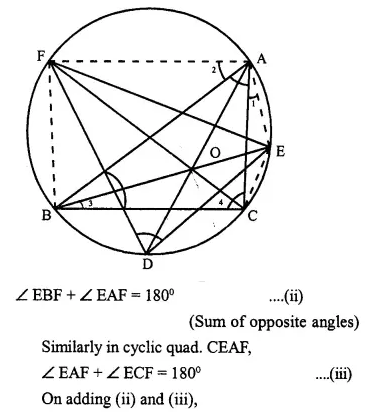
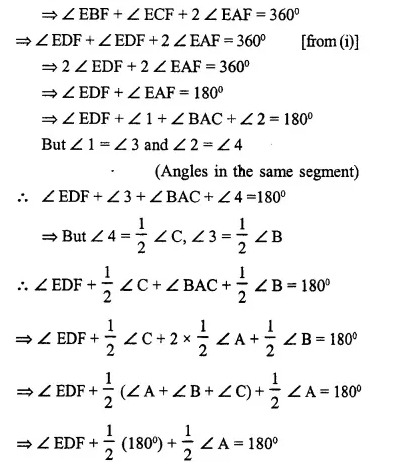
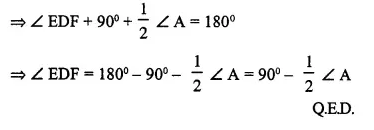
Question 11.
In the flgure; AB is the chord of a circle with centre O and DOC is a line segment such that BC = DO. If ∠ C = 20°, find angle AOD.
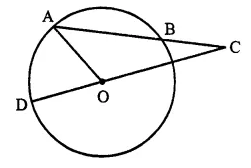
Solution:
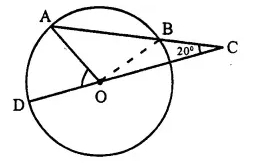
Join OB
In ∆ OBC, BC = OD = OB (radii of the circle)
∴ ∠ BOC = ∠ BCO = 20°
and Ext. ∠ ABO = ∠ BCO + ∠ BOC
= 20°+ 20° = 40° ….(i)
In ∆ OAB, OA = OB (radii of the circle)
∴ ∠ OAB = ∠ OBA = 40° [from (i)]
∠ AOB = 180°- ∠ OAB – ∠ OBA
= 180°-40°-40°= 100°
∵ DOC is a line
∴ ∠ AOD + ∠ AOB + ∠ BOC = 180°
⇒ ∠ AOD + 100° + 20° = 180°
⇒ ∠ AOD + 120° = 180°
∴ ∠ AOD = 180° – 120° = 60°
Question 12.
Prove that the perimeter of a right triangle is equal to the sum of the diameter of its incircle and twice the diameter of its circumcircle.
Solution:
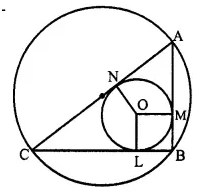
Given: In ∆ ABC, ∠ B = 90° which is inscribed in a circle and O is the incentre of the incircle of ∆ABC.
D and d are the diameters of circumcircle and incircle of ∆ ABC.
To Prove: AB +BC + CA = 2D + d.
Construction: Join OL, OM and ON.
Proof: In circumcircle of ∆ ABC,
∠ B = 90° (given)
∴ AB is the diameter of circumcircle i.e. AB = D.
Let radius of incircle = r
∴ OL = OM = ON = r
Now from B, BL, BM are the tangents to the incircle
∴ BL = OM = r
Similarly we can prove that:
AM = AN and CL = CN = R (radius)
(Tagents from the point outside the circle)
Now AB + BC + CA = AM + BM + BL + CL + CA
= AN + r + r + CN + CA
= AN + CN + 2r + CA
= AC + AC + 2r = 2 AC + 2r = 2D + d Q.E.D.
Question 13.
P is the mid point of an arc APB of a circle. Prove that the tangent drawn at P will be parallel to the chord AB.
Solution:
Given: A circle with centre O, AB is an arc whose mid point is P and AB is chord. TPS is the tangent at P.
To Prove: TPS ||AB.
Construction: Join AP and BP.
Prove: TPS is tangent and PA is chord of the circle
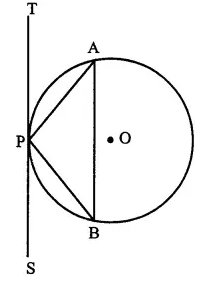
∠ APT = ∠ PBA (angles in the alternate segment)
But ∠ PBA = ∠ PAB (∵ PA = BP)
∴ ∠ APT = ∠ PAB
But these are alternate angles
∴ TPS || AB Q.E.D
Question 14.
In the given figure, MN is the common chord of two intersecting circles and AB is their common tangent Prove that the line NM produced bisects AB at P.
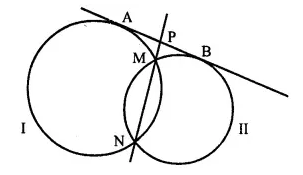
Prove that the line NM produced bisects AB at P.
Solution:
Given: Two circles intersect each other at M and N. AB is their common tangent, chord MN intersect the tangent at P.
To Prove: P is mid point of AB.
Proof: From P, AP is the tangent and PMN is the secant of first circle.
∴ AP2 = PM x PN ….(i)
Again from P, PB is the tangent and PMN is the secant of the second circle.
PB2 = PM x PN ….(ii)
from (i) and (ii)
AP2 = PB2 ⇒ AP = PB
∴ P is the mid point of AB. Q.E.D.
Question 15.
In the given figure, ABCD is a cyclic- quadrilateral, PQ is tangent to the circle at point C and BD is its diameter. If ∠ DCQ = 40° and ∠ ABD = 60°, find :
(i) ∠ DBC
(ii) ∠ BCP
(iii) ∠ ADB
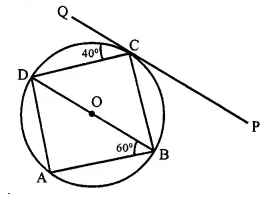
Solution:
(i) PQ is the tangent and CD is the chord
∴ ∠ DCQ = ∠ DBC (angles in the alternate segment)
∴ ∠ DBC = 40° (∵ ∠ DCQ = 40°)
(ii) ∠ DCQ + ∠ DCB + ∠ BCP = 180°
⇒ 40° + 900 + ∠ BCP = 180°(∵ ∠ DCB = 90°)
⇒ 130°+ ∠ BCP = 180°
∵ ∠ BCP =180° -130° = 50°
(iii) In Δ ABD, ∠ BAD = 90° (Angle in a semi circle) and ∠ ABD = 60°
∴ ∠ ADB = 180°- (60° + 90°)
⇒ 1800- 150° = 30°
Question 16.
The given figure shows a circle with centre O and BCD is tangent to it at C. Show that:
∠ ACD + ∠ BAC = 90°.
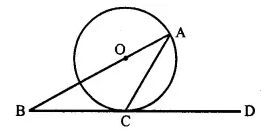
Solution:
Given: A circle with centie O and BCD is a tangent at C.
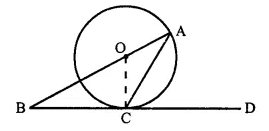
To Prove: ∠ ACD + ∠ BAC = 90°
Construction: Join OC.
Proof: BCD is the tangent and OC is the radius
∴ OC ⊥ BD
⇒ ∠ OCD = 90°
⇒ ∠ OCA + ∠ ACD = 90° ….(i)
But in ∆ OCA
OA = OC (radii of the same circle)
∴ ∠ OCA = ∠ OAC [from (i)]
∠OAC + ∠ACD = 90°
⇒ ∠ BAC + ∠ ACD = 90° Q.E.D.
Question 17.
ABC is a right triangle with angle B = 90°. A circle with BC as diameter meets hypotenuse AC at point D. Prove that
(i) AC x AD = AB2
(ii) BD2 = AD x DC.
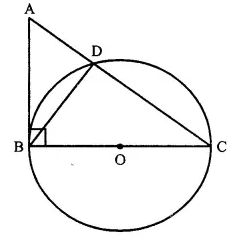
Solution:
Given: A circle with BC as diameter meets the hypotenuse of right ∆ ABC with ∠ B = 90° meets at D. BD is joined.
To Prove:
(i) AC x AD = AB2
(ii) BD2 = AD x DC
Proof:
(i) In ∆ABC, ∠ B = 90° and BC is the diameter of the circle.

Question 18.
In the given figure. AC = AE.
Show that :
(i) CP = EP
(ii) BP = DP.
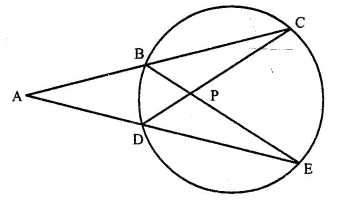
Solution:
Given: In the figure, AC = AE
To Prove: (i) CP = EP (ii) BP = DP
Proof: In ∆ ADC and ∆ ABE,
AC = AE (given)
∠ ACD = ∠ AEB (Angles in the same segment)
∠ A = ∠ A (Common)
∆ ADC ≅ ∆ ABE (ASA postulate)
AB = AD (C.P.C.T.)
But AC = AE (given)
∴ AC – AB = AE – AD
⇒ BC = DE
Now in ∆ BPC and ∆ DPE,
BC = DE (proved)
∠ C = ∠ E (Angles in the same segment)
∠ CBP = ∠ CDE (Angles in the same segment)
∴ ∆ BPC ≅ ∆ DPE (S.A.S. postulate)
∴ BP=DP (C.P.C.T.)
CP = PE (C.P.C.T.) Q.E.D.
Question 19.
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC = 120°.
Calculate :
(i) ∠ BEC
(ii) ∠ BED
Solution:
(i) In cyclic pentagon, O is the centre of circle.
Join OB, OC
AB = BC = CD (given)
and ∠ ABC = 120°.
∴ ∠ BCD = ∠ ABC = 120°
OB and OC are the bisectors of ∠ ABC and ∠ BCD respectively.
∴ ∠ OBC = ∠ BCO = 60°
In ∆ BOC,
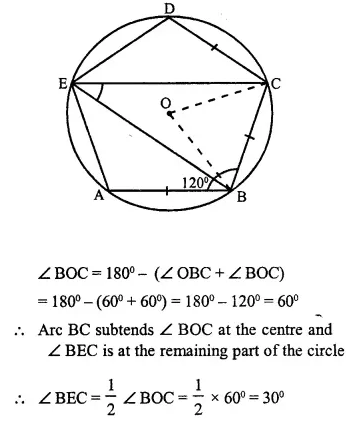
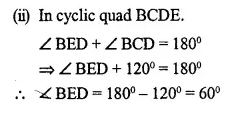
Question 20.
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If ∠ACO=30°, find
(i) ∠BCO
(ii) ∠AOB
(iii) ∠APB
Solution:
Given: In the fig. O is the centre of the circle CA and CB are the tangents to the circle from C. ∠ACO = 30°
P is any point on the circle. PA and PB are joined.
To find:
(i) ∠BCO
(ii) ∠AOB
(iii) ∠APB
Proof:
(i) In ∆ OAC and ∆OBC,
OC=OC (common)
OA = OB (radius of the circle)
CA = CB (tangents to the circle)
∴ ∆OAC ≅ ∆OBC (SSS axion)
∴ ∠ACO = ∠BCO = 30°
(ii) ∴ ∠ACB = 30° + 30° = 60°
∴ ∠AOB + ∠ACB = 180°
⇒ ∠AOB+ 60° =180°
∴ ∠AOB = 180° – 60° = 120°
(iii) Arc AB, subtends ∠AOB at the centre and ∠APB is in the remaining part of the circle
∴ ∠APB = \(\frac { 1 }{ 2 }\) ∠AOB = \(\frac { 1 }{ 2 }\) x 120° = 60°
Question 21.
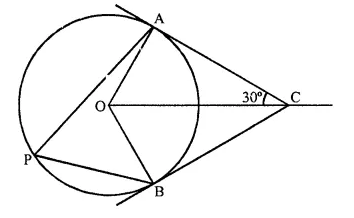
ABC is triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles. (2011)
Solution:
Given: ABC is a triangle with AB = 10 cm, BC = 8 cm, AC = 6 cm. Three circle are drawn with centre A, B and C touch each other at P, Q and R respectively

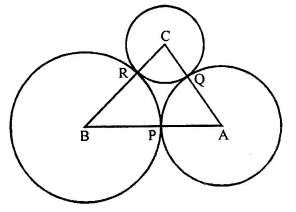
Question 22.
In a square ABCD, its diagonals AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and the bisector of angle ABD meets AC at N and AM at L.
Show that :
(i) ∠ ONL + ∠ OML = 180°
(ii) ∠ BAM = ∠ BMA
(iii) ALOB is a cyclic quadrilateral
Solution:
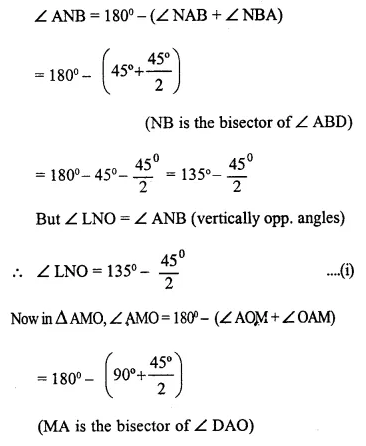

Question 23.
The given figure shows a semi-circle with centre O and diameter PQ. If PA = AB and ∠ BCQ = 140°; find measures of angles PAB and AQB. Also, show that AO is parallel to BQ.
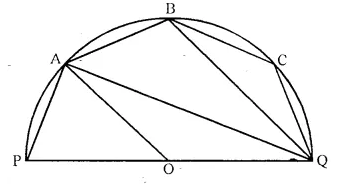
Solution:
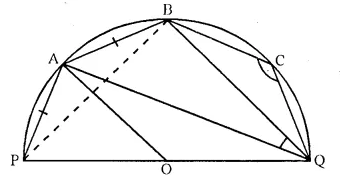
Join PB
In cyclic quad. PBCQ,
∠ BPQ + ∠ BCQ = 180°
⇒ ∠ BPQ + 140° = 180°
∴ ∠ BPQ = 180° – 140° = 40°
Now, in ∆ PBQ,
∠ PBQ + ∠ BPQ + ∠ BQP = 180°
⇒ 90° + 40° + ∠ BQP = 180°
(∠ PBQ = 90° angle in a semicircle)
⇒ 130° + ∠ BQP = 180°
∴ ∠ BQP = 180° – 130°= 50°
Nowin cyclic quad. PQBA,
∠ PQB + ∠ PAB = 180°
⇒ 50° + ∠ PAB = 180°
∴ ∠ PAB = 180° – 50° = 130°
(ii) Now, in ∆ PAB,
∠ PAB + ∠ APB + ∠ ABP = 180°
⇒ 130° + ∠ APB + ∠ ABP = 180°
⇒ ∠ APB + ∠ ABP = 180° – 130° = 50°
But ∠ APB = ∠ ABP = 25°
∴ (PA = AB)
∠ BAQ = ∠ BPQ = 40°
(Angles in the same segment)
Now, in ∆ ABQ,
∠ AQB + ∠ QAB + ∠ ABQ = 180°
⇒ ∠ AQB + 40° + 115° = 180°
⇒ ∠ AQB + 155° = 180°
⇒ ∠ AQB = 180° – 155° = 25°
(iii) Arc AQ subtends ∠ AOQ at the centre and ∠APQ at the remaining part of the circle,
∠ AOQ = 2 ∠ APQ = 2 x 65° = 130°
Now, in ∆ AOQ,
∠ OAQ = ∠ OQA
(∵ OA = OQ radii of the same circle)
But ∠ OAQ + ∠ OQA + ∠ AOQ = 180°
⇒ ∠ OAQ + ∠ OAQ + 130° = 180°
2 ∠ OAQ = 180° – 130° = 50°
∴ ∠ OAQ = 25°
∵ ∠ OAQ = ∠ AQB (each = 25°)
But these are alternate angles.
∴ AO || BQ.
Q.E.D.
Question 24.
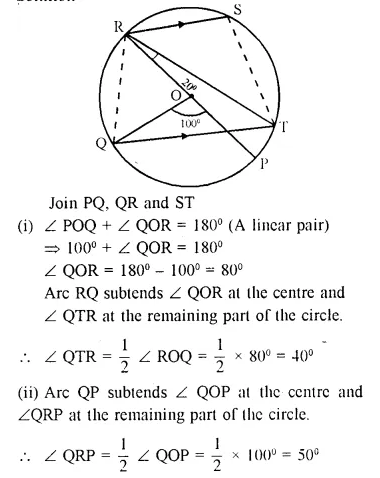
The given figure shows a circle with centre O such that chord RS is parallel to chord QT, angle PRT = 20° and angle POQ = 100°. Calculate
(i) angle QTR
(ii) angle QRP
(iii) angle QRS
(iv) angle STR
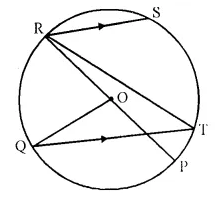
Solution:

Question 25.
In the given figure, PAT is tangent to the circle with centre O, at point A on its circumference and is parallel to chord BC. If CDQ is a line segemcnt, show that :
(i) ∠ BAP = ∠ ADQ
(ii) ∠ AOB = 2 ∠ ADQ
(iii) ∠ ADQ = ∠ ADB
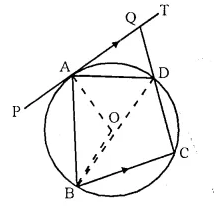
Solution:
Given: PAT is the tangent to the circle with centre O, at A. Chord BC || PAT is drawn.
CDQ is a line segment which intersects the circle at C and D and meets the tangent PAT at Q.
To Prove:
(i) ∠ BAP = ∠ ADQ (ii)∠ AOB = 2 ∠ ADQ
(iii) ∠ ADQ = ∠ ADB
Proof:
(i) ∵ PAT || BC
∴ ∠ PAB = ∠ ABC (Alternate angles) ….(i)
In cyclic quad. ABCD,
Ext. ∠ADQ = ∠ABC ….(ii)
∴ ∠ PAB = ∠ ADQ (from (i) and (ii))
(ii) Arc AB subtends ∠ AOB at the centre and ∠ADB at the remaining part of the circle.
∴ ∠ AOB = 2 ∠ ADB
= 2 ∠ PAB (In the alt. segment)
= 2 ∠ ADQ [proved in (i)]
(iii) ∵ ∠ BAP = ∠ ADB
(Angles in the alt. segment)
Bui ∠ BAP = ∠ ADQ (Proved in (i))
∴ ∠ ADQ = ∠ ADB Q.E.D.
Question 26.
AB is a line segment and M is its mid-point. Three semi-circles are drawn with AM, MB and AB as diameters on the same side of the line AB. A circle with radius r unit is drawn so that it touches all the three semi-circles. Show that: AB = 6 x r
Solution:
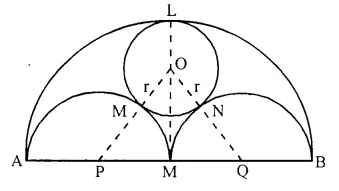
Given: A line segment AB whose mid-point is M. Three circles are drawn on AB, AM and MB as diameler A circle with radius r is drawn which touches (he three circles externally at L, R and N respectively. M, P, Q are the centres of the three circles.
To Prove: AB= 6r
Construction: Join OP and OQ.
Proof: OM = ON = r

Question 27.
TA and TB are tangents to a circle with centre O from an external point T. OT intersects the circle at point P. Prove that AP bisects the angle TAB.
Solution:
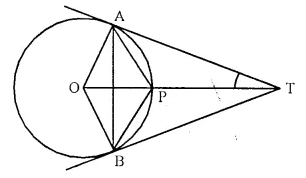
Given: A circle with centre C. From a point T outside th circle, TA and TB are two tangent to the circle OT intersects the circle at P, AP and AB are joined.
To Prove: AP is the bisector of ∠ TAB
Construction: Join PB.

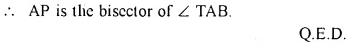
Question 28.
Two circles intersect in points P and Q. A secant passing through P intersects the circles in A and B respectively. Tangents to the circles at A and B intersect at T. Prove that A, Q, B and T lie on a circle.
Solution:
Given: Two circles intersect each other at P and Q. From P, a secant intersects the circles at A and B respectively. From A and B tangents are drawn which intersect each other at T.
To Prove: A. Q, B and T on a circle.
Construction: Join PQ.
Proof: AT is the tangent and AP is chord
∴ ∠ TAP = ∠ AQP (Angles in all. segment) …(i)
Similarly ∠ TBP = ∠ BQP ….(ii)
Adding (i) and (ii),
∠ TAP + ∠ TBP = ∠ AQP + ∠ BQP = ∠ AQB …..(iii)
Now, in ∆ TAB,
∠ ATB + ∠ TAP + ∠ TBP = 180°
⇒ ∠ ATB + ∠ AQB = 180° (from (iii)
∴ AQBT is a cyclic quadrilateral.
Hence A, Q, B and T lie on the same circle. Q.E.D.
Question 29.
Prove that any four vertices of a regular pentagon are concyclic (lie on the same circle).
Solution:
ABCDE is a regular pentagon.
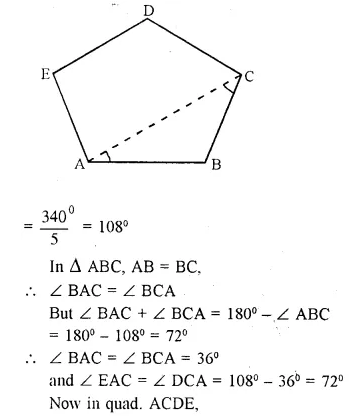

To Prove: Any four vertices lie on the same circle.
Construction: Join AC.
Proof: Each angle of a regular pentagon
Question 30.
Chords AB and CD of a circle when extended meet at point X. Given AB = 4 cm, BX = 6 cm and XD = 5 cm, calculate the length of CD. [2000]
Solution:
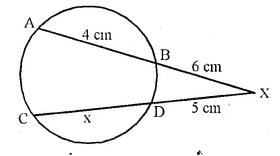
Let CD = x
∴ chords AB and CD intersect each other at outside the circle.
∴ AX.XB = CX.XD
⇒(4+6)x6 = (x + 5)x5
⇒ 10 x 6 = 5x + 25
⇒ 60 = 5x + 25
⇒ 5x = 60 – 25 = 35
∴ x = \(\frac { 35 }{ 5 }\) = 7
CD = 7 cm
Question 31.
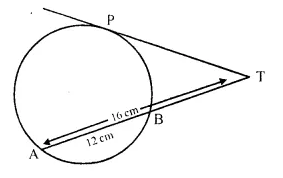
in the given figure. find TP if AT = 16 cm AB = 12 cm.
Solution:
In the figure.
PT is the tangent and TBA is the secant of the circle.
∴ TP2 = TA x TB = 16 x (16 – 12) = 16 x 4 = 64 = (8)2
Hence, TP = 8 cm.
Question 32.
In the following figure, a circle is inscribed in the quadrilateral ABCD. If BC = 38 cm. QB = 27 cm, DC = 25 cm and that AD is perpendicular to DC, find the radius of the circle. (1990)
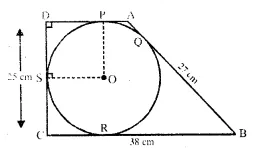
Solution:
A circle with centre is inscribed (see the fig.)
in a quadrilateral ABCD. BC = 38 cm, QB = 27cm,
DC = 25 cm and AD ⊥ BC.
Join OP and QS.
∵ OP and OS are the radii of the circle
∴ OP ⊥ AD and OS ⊥ CD
∴ OPDS is a square
∴ OP = OS – DP = DS.
Let length of radius of the circle = r
then DP = DS = r
∴ CS = 25 – r
∵ EQ = BR = 27 cm (tangents to the circle from B)
∴ CR = BC – BR = 38 – 27 = 11 cm
Similarly CR = CS
∴ 25 – r = 11 ⇒ r = 25 – 11 = 14
∴ Radius of the circle = 14 cm
Question 33.
In the given figure, XY is the diameter of the circle and PQ is a tangent to the circle at Y.
If ∠AXB = 50° and ∠ABX = 70°, find ∠BAY and ∠APY.
Solution:
In the above figure,
XY is a diameter of the circle PQ is tangent to the circle at Y.
∠AXB = 50° and ∠ABX = 70°
(i) In ∆AXB,
∠XAB + ∠ABX + ∠AXB = 180° (Angles of a triangle)
⇒ ∠XAB + 70° + 50° = 180°
⇒ ∠XAB + 120° =180°
⇒ ∠XAB = 180° – 120° = 60°
But, ∠XAY = 90° (Angle in a semicircle)
∴ ∠BAY = ∠XAY-∠XAB=90°- 60° = 30°
(ii) Similarly ∠XBY=90°(Angle in a semicircle) and ∠CXB = 70°
∴ ∠PBY = ∠XBY-∠XBA =90° – 70° = 20°
∵ ∠BYA = 180° – ∠AXB ( ∵ ∠BYA + ∠AYB = 180°) = 180°- 50° = 130°
∠PYA =∠ABY (Angles in the alternate segment) = ∠PBY = 20°
and ∠PYB = ∠PYA + ∠AYB
= 20° + 130° = 150°
∴ ∠APY = 180°-(∠PYA + ∠ABY)
= 180° -(150° +20°) =180° – 170° = 10°
Question 34.
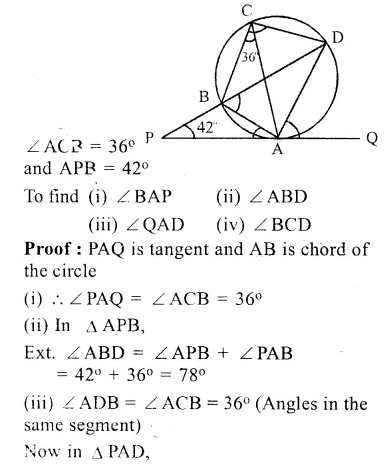
In the given figi QAP is the tangent point A and PBD is a straight line. If ∠ACB = 36° and ∠APB = 42°, find:
(i) ∠ BAP
(ii) ∠ABD
(iii) ∠ QAD
(iv) ∠ BCD
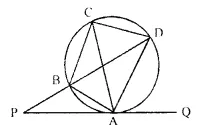
Solution:
In the given figure, QAP is the tangent to the circle at A and PBD is a B straight line.
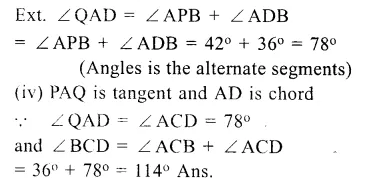
Question 35.
In the given figure, AB is a diameter. The tangent at C meets AB produced at Q. If ∠ CAB = 34°,
find :
(i) ∠CBA
(ii) ∠CQB
Solution:
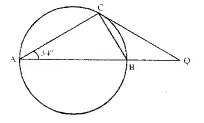
In ∆ ABC,
we have ∠ ACB = 90°
[Angle in a semicircle is 90°]
(i) Also ∠ CBA + ∠ CAB + ∠ ACB = 180° [Angle sum property of a ∆ ]
⇒ ∠ CBA =180°- ∠ CAB – ∠ ACB = 180°-34°-90° = 180°-124° = 56°
(ii) CQ is a tangent at C and CB is a chord of the circle.
⇒ ∴ ∠ QCB = ∠ BAC = 34° [Angles in the alternate segments]
∠ CBQ =180°- ∠ ABC [Linear pair]
⇒ ∠ CBQ = 180°- 56° = 124° [From (i)]
In ∆ BCQ, we have
⇒ ∠ CQB = 180° – (∠ QCB + ∠ CBQ) [Angle sum property of a ∆ ]
= 180° -(34° + 124°) = 180°- 158° = 22°
Hence, ∠CQB = 22°
Question 36.
In the given figure, A O is the centre of the circle. The tangents at B and D intersect each other at point P.
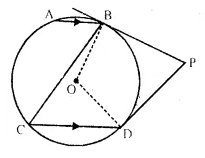
If AB is parallel to CD and ∠ ABC = 55
find :
(i) ∠ BOD
(ii) ∠ BPD
Solution:
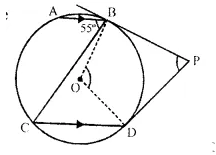
In the given figure,
O is the centre of the circle AB || CD,
∠ ABC = 55° tangents at B and D are drawn which meet at P.
∵ AB || CD
∴ ∠ ABC = ∠ BCD (Alternate angles)
∴ ∠ ABC = 55° (Given)
(i) Now arc BD subtands ∠ BOD at the centre and ∠ BCD at the remaining part of the circle.
∴ ∠BOD = 2∠BCD = 2 x 55° = 110°
(ii) In quad. OBPD,
∠OBP = ∠ODP = 90° (∵ BP and DP are tangents)
∴ ∠BOD + ∠BPD = 180°
⇒ 110° +∠BPD =180°
⇒ ∠BPD =180°-110°= 70°
Hence, ∠BOD = 110° and ∠BPD = 70°
Question 37.
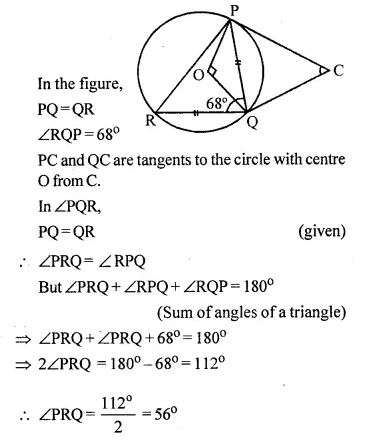
In the figure given below PQ = QR, ∠RQP = 68°, PC and CQ are tangents to the circle with centre O. Calculate the values of:
(i) ∠QOP
(ii) ∠QCP
Solution:

Question 38.
In two concentric circles, prove that all chords of the outer circle, which touch the inner circle, are of equal length.
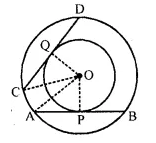
Solution:
Given: Two concentric circles with centre O AB and CD are two cords of outer circle which touch the inner circle at P and Q respectively
To prove: AB = CD
Construction : Join OA, OC, OP and OQ
Proof: ∵ OP and OQ are the radii of the inner circle and AB and CD are tangents
∴ OP ⊥ AB and OQ ⊥ CD
and P and Q are the midpoints of AB and CD Now in right AOAP and OCQ,
Side OP = OQ (radii of the inner circle)
Hyp. OA = OC (radii of the outer circle)
∴ ∆OAP = ∆OCQ (R.H.S. axiom)
∴ AP = CQ (c.p.c.t.)
But AP = \(\frac { 1 }{ 2 }\) AB and CQ = \(\frac { 1 }{ 2 }\) CD
∴ AB = CD Hence proved.
Question 39.
In the figure, given below, AC is a transverse common tangent to two circles with centres P and Q and of radii 6 cm and 3 cm respectively.
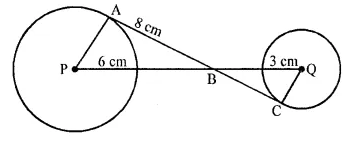
Given that AB = 5 cm , Calculate PQ.
Solution:
In the figure, two circles with centres P and Q and radii 6 cm and 3 cm respectively
ABC is the common transverse tangent to the two circles. AB = 8 cm
Join AP and CQ
∵ AC is the tangents to the two circles and PA and QC are the radii

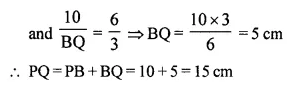
Question 40.
In the figure, given below, O is the centre of the circumcircle of triangle XYZ. Tangents at X and Y intersect at point T. Given ∠XTY = 80° and ∠XOZ = 140°, calculate the value of ∠ZXY.
Solution:
In the figure, a circle with centre O, is the circumcircle of ∆XYZ.
∠XOZ =140° (given)
Tangents from X and Y to the circle meet at T such that ∠XTY = 80°
∵ ∠XTY = 80°
∴ ∠XOY= 180°-80°= 100°
But ∠XOY + ∠YOZ + ∠XOZ = 360° (Angles at a point)
⇒ 100°+∠YOZ+ 140o = 360o
⇒ 240o+∠YOZ =360°
⇒ ∠YOZ =360°- 240°
⇒∠YOZ =120°
Now arc YZ subtends ∠YOZ at the centre and ∠YXZ at the remaining part of the circle
∴ ∠YOZ = 2 ∠YXZ
⇒ ∠YXZ= \(\frac { 1 }{ 2 }\) ∠YOZ ⇒ ∠YXZ = \(\frac { 1 }{ 2 }\) x 120° = 60°
Question 41.
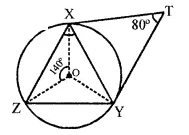
In the given figure, AE and BC intersect each other at point D. If ∠CDE = 90°, AB = 5 cm, BD = 4 cm and CD = 9 cm, findAE.
Solution:
In the given circle,
Chords AE and BC interesect each other at D at right angle i.e., ∠CDE = 90°, AB is joined AB = 5cm, BD = 4 cm, CD = 9 cm
Now we have to find AE.
Let DE=xm
Now in right ∆ABD,
AB2 = AD2 + BD2 (Pythagoras Theorem)
⇒ (5)2=AD2 + (4)2
⇒ 25 = AD2 + 16
⇒ AD2 = 25-16 = 9 = (3)2
∴AD = 3cm
∵ Chords AE and BC intersect eachothcr at D inside the circle
∴ AD x DE = BD x DC
⇒ 3 x x = 4 x 9
⇒ x= \(\frac { 4×9 }{ 3 }\) = 12cm;
∴ AE=AD + DE = 3 + 12 = 15 cm
Question 42.
In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.
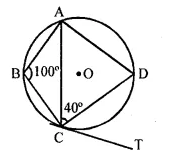
Solution:
ABCD is a cyclic quadrilateral
∴ ∠ABC + ∠ADC = 180°
100° +∠ADC = 180°
∠ADC = 180°- 100° = 80°
In ∆ADC
∠ACD + ∠CDA + ∠D AC =180°
40° + 80° +∠D AC = 180°
∠D AC = 180° – 80° – 40° = 60°
Now ∠DAC = 60°
⇒ ∠DCT = 60° [angle in alt. segment]
Question 43.
In the figure given below, O is the centre of the circle and SP is a tangent. If ∠SRT = 65°, find the values of x,y and z. (2015)
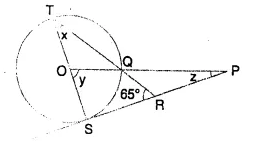
Solution:
In the given figure,
O is the centre of the circle.
SP is tangent ∠SRT =65°.
To find the values of x, y and z
(i) In ∆STR,
∠S = 90° (∵ OS is radius and ST is tangent)
∴ ∠T + ∠R = 90°
⇒ x + 65° = 90°
⇒ x = 90° – 65° = 25°
(ii) Arc CQ subtends ∠SOQ at the centre and
∠STQ at the remaining part of the circle.
∠y = ∠QOS = 2∠T = 2∠x = 2 x 25° = 50°
(iii) In ∆OSP,
∠S = 90°
∴ ∠SOQ or ∠SOP + ∠P = 90°
⇒ y+z=90o
⇒ 50° + z = 90°
⇒ z = 90°-50° = 40°
Hence x = 25°, y = 50° and z = 40°
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 18 Tangents and Intersecting Chords Ex 18C are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.