Selina Concise Mathematics Class 10 ICSE Solutions Chapter 13 Section and Mid-Point Formula Ex 13B
These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 13 Section and Mid-Point Formula Ex 13B.
Other Exercises
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 13 Section and Mid-Point Formula Ex 13A
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 13 Section and Mid-Point Formula Ex 13B
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 13 Section and Mid-Point Formula Ex 13C
Question 1.
Find the mid-point of the line segment joining the points:
(i) (-6, 7) and (3, 5)
(ii) (5, -3), (-1, 7)
Solution:
Let P (x, y) be the mid-point in each case
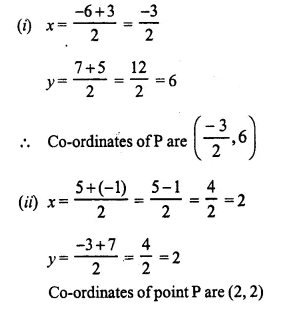
Question 2.
Points A and B have co-ordinates (3, 5) and (x, y) respectively. The mid-point of AB is (2, 3). Find the values of x and y.
Solution:
Co-ordinates of A (3, 5), B (x, y) and mid-point M (2, 3)
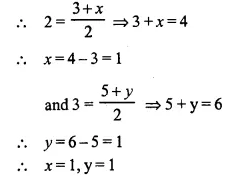
Question 3.
A (5, 3), B (-1, 1) and C (7, -3) are the vertices of ABC. If L is the mid-point of AB and M is the mid-point of AC, show that LM = \(\frac { 1 }{ 2 }\) BC.
Solution:
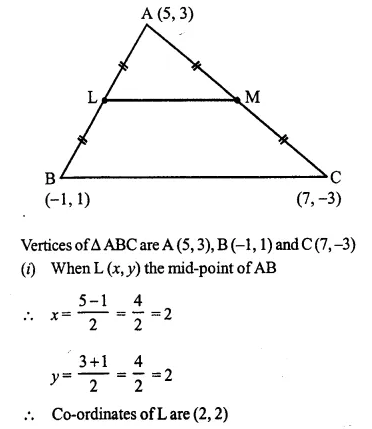
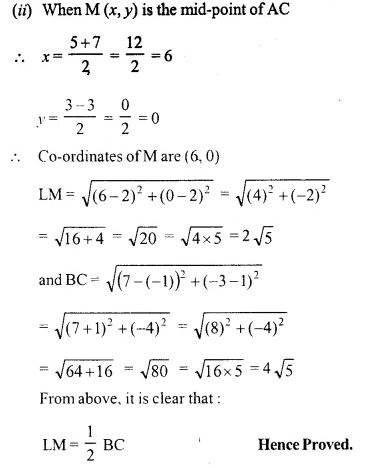
Question 4.
Given M is the mid-point of AB, find the co-ordinates of:
(i) A; if M = (1, 7) and B = (-5, 10),
(ii) B; if A = (3, -1) and M (-1, 3).
Solution:
M is the mid-point of AB.
(i) Let A = (x, y), M = (1, 7) and B = (-5, 10)
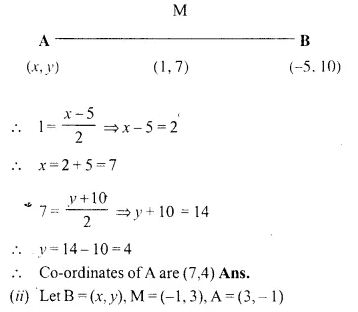
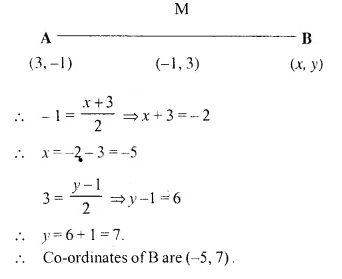
Question 5.
P (-3, 2) is the mid-point of line segment AB as shown in the figure. Find the co-ordinates of points A and B.
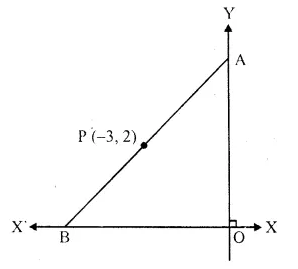
Solution:
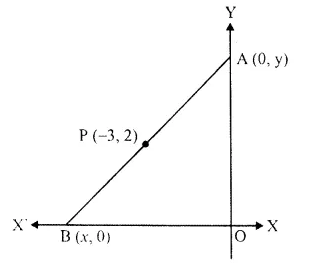
Point A is on y-axis
its abscissa is zero and point B is on x-axis
its ordinate is zero.
Now, let co-ordinates of A are (0, y) and ofB are (x, 0) and P (-3, 2) is the mid-point
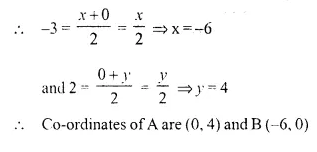
Question 6.
In the given figure, P (4, 2) is the mid point of line segment AB. Find the co-ordinates of A and B.
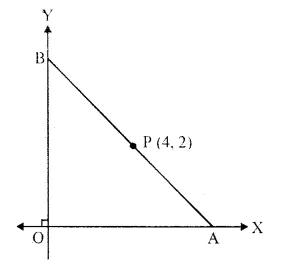
Solution:
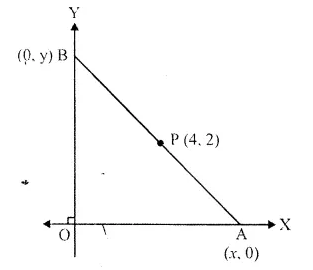
Points A and B are on x-axis and y-axis respectively
Ordinate of A is zero and abscissa of B is zero.
Let co-ordinates of A be (x, 0) and B (0, y)
and P (4, 2) is the mid-point
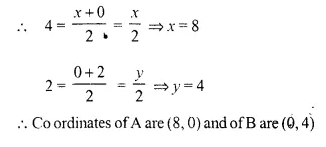
Question 7.
(-5, 2), (3, -6) and (7, 4) arc the vertices of a triangle. Find the length of its median through the vertex (3, -6) and (7, 4).
Solution:
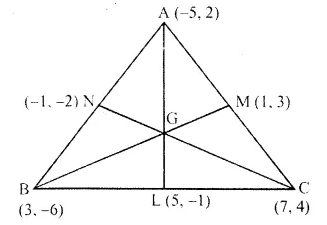
Let A (-5, 2), B (3, -6) and C (7, 4) are the vertices of a ABC
Let L,M and N are the mid-points of sides BC, CA and AB respectively of ABC.
L is the mid-point of BC.
Co-ordinates of L will be

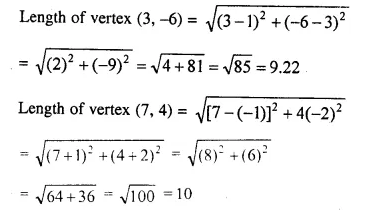
Question 8.
Given a line ABCD in which AB = BC = CD, B = (0, 3) and C = (1, 8). Find the co-ordinates of A and D.
![]()
Solution:

![]()
Question 9.
One end of the diameter of a circle is (-2, 5). Find the co-ordinates of the other end of it, if the centre of the circle is (2, -1).
Solution:
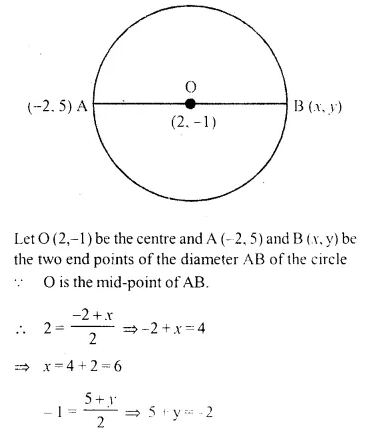
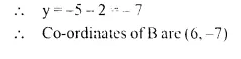
Question 10.
A (2, 5), B (1, 0), C (-4, 3) and D (-3, 8) are the vertices of quadrilateral ABCD. Find the co-ordinates of the mid-points of AC and BD. Give a special name to the quadrilateral.
Solution:
Co-ordinates of A = (2, 5), B = (1, 0), C = (-4, 3) and D = ( 3, 8)
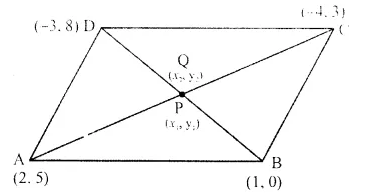
Let the mid-point of AC is P (x1, y1) Co-ordinates of mid-point of AC will be
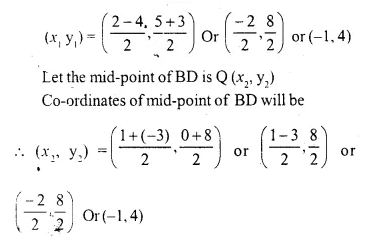
Co-ordinates of mid-points AC and BD are the same..
The quadrilateral is a parallelogram.
Question 11.
P (4, 2) and Q (-1, 5) are the vertices of parallelogram PQRS and (-3, 2) are the co-ordinates of the point of intersection of its diagonals. Find the co-ordinates of R and S.
Solution:
In the parallelogram PQRS and qo-ordinates of P are (4, 2) and of Q are (-1, 5).
The diagonals of || gm AC and BD intersect each other at O (-3, 2)

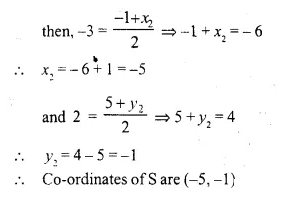
Question 12.
A (-1, 0), B (1, 3) and D (3, 5) are the vertices of a parallelogram ABCD. Find the co-ordinates of vertex C.
Solution:
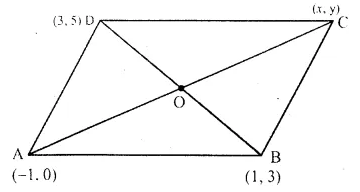
Vertices of a parallelogram ABCD are A (-1, 0), B (1, 3) and D(3, 5)
Let co-ordinates of C be (x, y)
Let the diagonals AC and BD bisect each other at O. Then O is the mid-point of AC as well as of BD.
Co-ordinates of O, the mid-point of BD will be
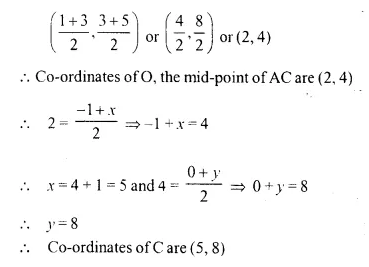
Question 13.
The points (2, -1), (-1, 4) and (-2, 2) are the mid-points of the sides of a triangle. Find its vertices.
Solution:
Let D, E and F are the mid-points of sides BC, CA and AB of a ABC respectively.
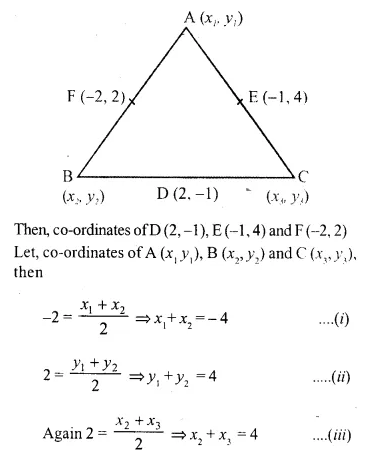

Co-ordinates of A are (-5, 7), of B are (1, -3) and of C are (3, 1)
Question 14.
Points A (-5, x), B (y, 7) and C (1, -3) are collinear (i.e. lie on the same straight line) such that AB = BC. Calculate the values of x and y.
Solution:
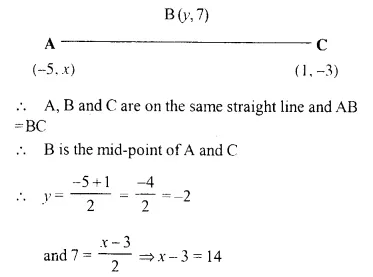
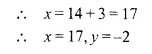
Question 15.
Points P (a, -4), Q (-2, b) and R (0, 2) are collinear. If Q lies between P and R, such that PR = 2QR, calculate the values of ‘a’ and ‘b’:
Solution:

Question 16.
Calculate the co-ordinates of the centroid of the triangle ABC, if A = (7, -2), B = (0, 1) and C = (-1, 4).
Solution:
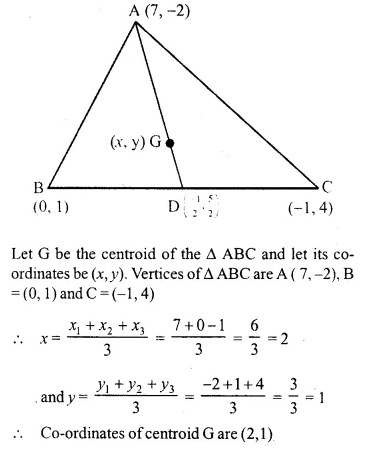
Question 17.
The co-ordinates of the centroid of a triangle PQR are (2, -5). If Q = (-6, 5) and R = (11, 8); calculate the co-ordinates of vertex P.
Solution:
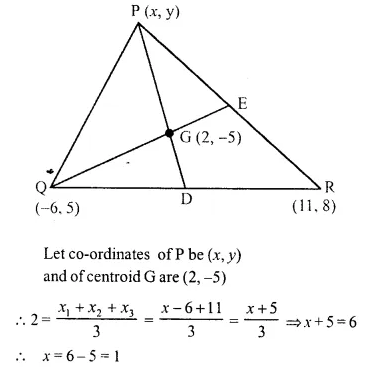
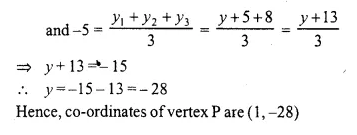
Question 18.
A (5, x), B (-4, 3) and C (y, -2) are the vertices of the triangle ABC whose centroid is the origin. Calculate the values of x and y.
Solution:
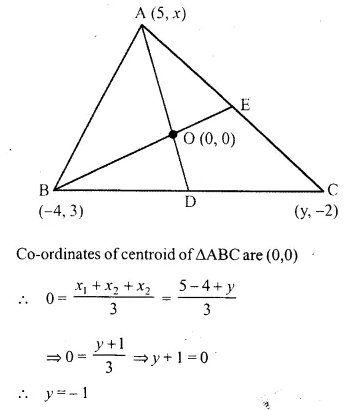
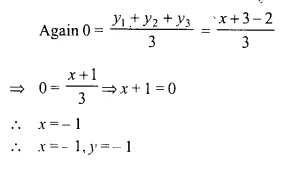
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 13 Section and Mid-Point Formula Ex 13B are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.