RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.4
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.4
Question 1.
Find the following products:
(i) (3x + 2y) (9X2 – 6xy + Ay2)
(ii) (4x – 5y) (16x2 + 20xy + 25y2)
(iii) (7p4 + q) (49p8 – 7p4q + q2)
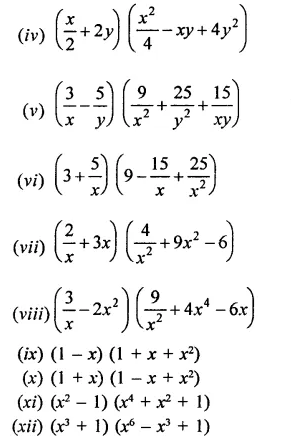
Solution:
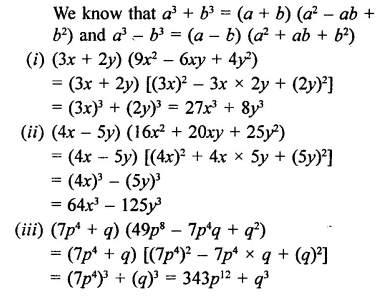
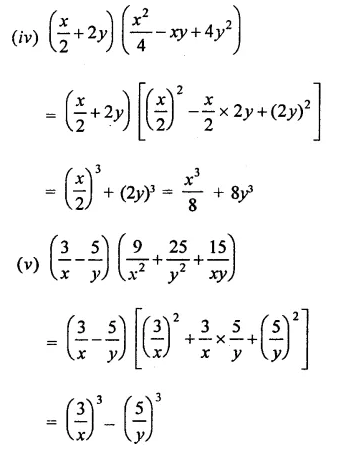
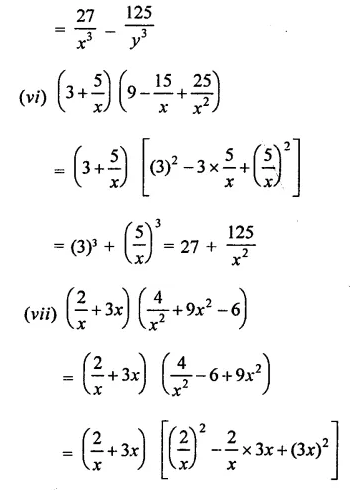
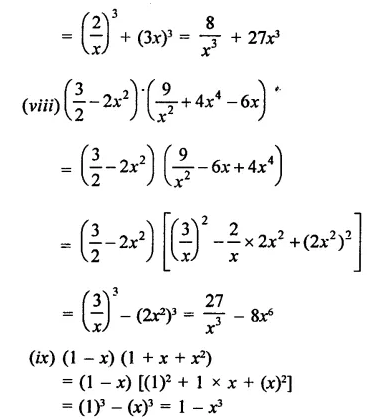
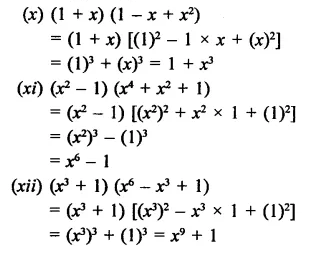
Question 2.
If x = 3 and y = -1, find the values of each of the following using in identity:
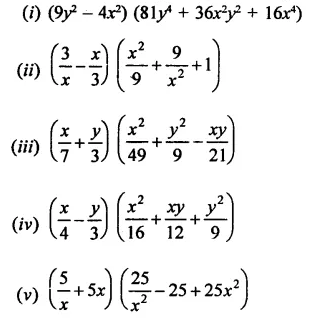
Solution:
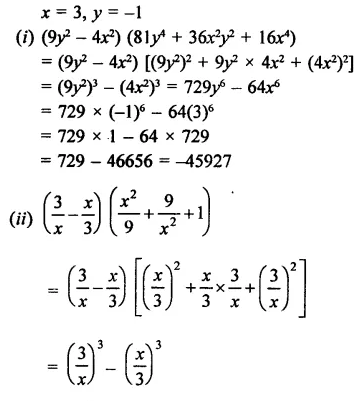
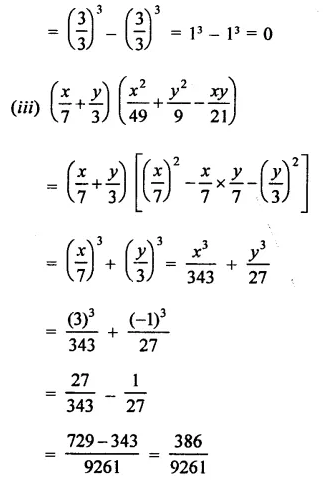
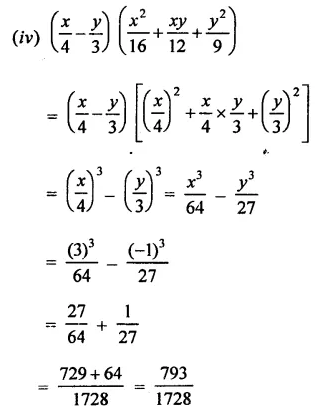
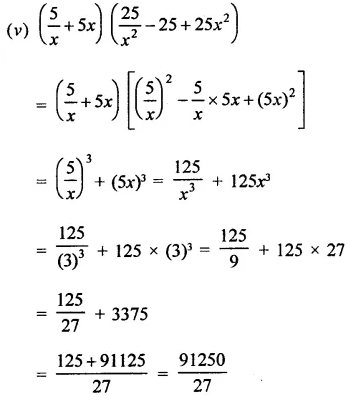
Question 3.
If a + b = 10 and ab = 16, find the value of a2 – ab + b2 and a2 + ab + b2.
Solution:
a + b = 10, ab = 16 Squaring,
(a + b)2 = (10)2
⇒ a2 + b2 + lab = 100
⇒ a2 + b2 + 2 x 16 = 100
⇒ a2 + b2 + 32 = 100
∴ a2 + b2 = 100 – 32 = 68
Now, a2 – ab + b2 = a2 + b2 – ab = 68 – 16 = 52
and a2 + ab + b2 = a2 + b2 + ab = 68 + 16 = 84
Question 4.
If a + b = 8 and ab = 6, find the value of a3 + b3.
Solution:
a + b = 8, ab = 6
Cubing both sides,
(a + b)3 = (8)3
⇒ a3 + b3 + 3 ab{a + b) = 512
⇒ a3 + b3 + 3 x 6 x 8 = 512
⇒ a3 + b3 + 144 = 512
⇒ a3 + b3 = 512 – 144 = 368
∴ a3 + b3 = 368
Question 5.
If a – b = 6 and ab = 20, find the value of a3-b3.
Solution:
a – b = 6, ab = 20
Cubing both sides,
(a – b)3 = (6)3
⇒ a3 – b3 – 3ab(a – b) = 216
⇒ a3 – b3 – 3 x 20 x 6 = 216
⇒ a3 – b3 – 360 = 216
⇒ a3 -b3 = 216 + 360 = 576
∴ a3 – b3 = 576
Question 6.
If x = -2 and y = 1, by using an identity find the value of the following:
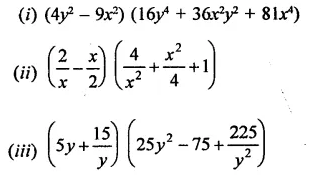
Solution:
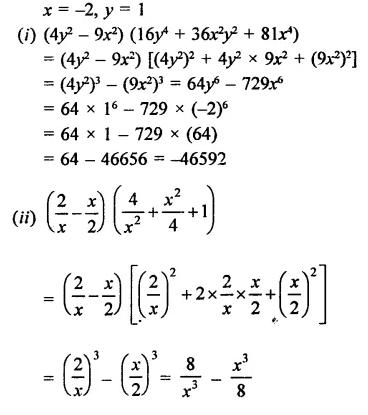
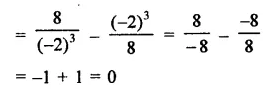
Hope given RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.4 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.