RD Sharma Class 9 Solutions Chapter 22 Tabular Representation of Statistical Data MCQS
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 22 Tabular Representation of Statistical Data MCQS
Other Exercises
- RD Sharma Class 9 Solutions Chapter 22 Tabular Representation of Statistical Data Ex 22.1
- RD Sharma Class 9 Solutions Chapter 22 Tabular Representation of Statistical Data Ex 22.2
- RD Sharma Class 9 Solutions Chapter 22 Tabular Representation of Statistical Data MCQS
Mark the correct alternative in each of the following:
Question 1.
Tally marks are used to find
(a) class intervals
(b) range
(c) frequency
(d) upper limits
Solution:
Frequency (c)
Question 2.
The difference between the highest and lowest values of the observations is called
(a) frequency
(b) mean
(c) range
(d) class intervals
Solution:
range (c)
Question 3.
The difference between the upper limit and the lower class limits is called
(a) mid-points
(b) class size
(c) frequency
(d) mean
Solution:
class size (b)
Question 4.
In the class intervals 10-20, 20-30, 20 is taken in
(a) the interval 10-20
(b) the interval 20-30
(c) both interval 10-20, 20-30
(d) none of the intervals
Solution:
the interval 20-30 (b)
Question 5.
In a frequency distribution, the mid value of a class is 15 and the class intervals is 4. The lower limit of the class is
(a) 10
(b) 12
(c) 13
(d) 14
Solution:
Mid value = 15 and class interval is 4
∴ Lower limit = 15 – \(\frac { 4 }{ 5 }\) = 15 – 2 = 13 (c)
Question 6.
The mid-value of a class interval is 42. If the class size is 10, then the upper and lower limits of the class are
(a) 47 and 37
(b) 37 and 47
(c) 37.5 and 47.5
(d) 47.5 and 37.5
Solution:
Mid value = 42 and class size =10
∴ Upper limit = 42 + \(\frac { 10 }{ 2 }\) = 42 + 5 = 47
and lower limit = 42 – \(\frac { 10 }{ 2 }\) = 42 – 5 = 37
Upper class limit and lower class limits are 47, 37 (a)
Question 7.
The number of times a particular item occurs in a given data is called its
(a) variation
(b) frequency
(c) cumulative frequency
(d) class-size
Solution:
frequency (b)
Question 8.
The width of each of nine classes in a frequency distribution is 2.5 and the lower class boundary of the lowest class 10.6. Then the upper class boundary of the highest class is
(a) 35.6
(b) 33.1
(c) 30.6
(d) 28.1
Solution:
Width of each class = 2.5
No. of classes = 9
Lower class boundary of the lowest class = 10.6
∴ Upper class limit of highest class = 10.6 + 9 x 2.5
= 10.6 + 22.5 = 33.1 (b)
Question 9.
The following marks were obtained by the students in a test:
81, 72, 90, 90, 86, 85, 92, 70, 71, 83, 89, 95, 85, 79, 62
The range of the marks is
(a) 9
(b) 17
(c) 27
(d) 33
Solution:
Marks are 81, 72, 90, 90, 86, 85, 92, 70, 71, 83, 89, 95, 85, 79, 62
Here highest marks = 95
and lowest marks = 62
∴ Range = highest marks – lowest marks = 95 – 62 = 33 (d)
Question 10.
Tallys are usually marked in a bunch of
(a) 3
(b) 4
(c) 5
(d) 6
Solution:
4 i.e. IIII (b)
Question 11.
Let l be the lower class limit of a class- interval in a frequency distribution and m be the mid-point of the class. Then, the upper class limit of the class is
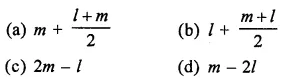
Solution:
l is the lower class limit of a class interval
m is the mid point of the class
m = \(\frac { u+l }{ 2 }\)
⇒ 2m = u+ l ⇒ u = 2m – l
Then, upper class limit = 2 m – l (c)
Hope given RD Sharma Class 9 Solutions Chapter 22 Tabular Representation of Statistical Data MCQS are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.