RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.3
These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.3
Other Exercises
- RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.1
- RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.2
- RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.3
- RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.4
- RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.5
Question 1.
Find the cube roots of the following numbers by successive subtraction of numbers : 1, 7, 19, 37, 61, 91, 127, 169, 217, 271, 331, 397,
(i) 64
(ii) 512
(iii) 1728
Solution:
(i) 64
64 – 1 = 63
63 – 7 = 56
56 – 19 = 37
37 – 37 = 0
∴ 64 = (4)3
∴ Cube root of 64 = 4
(ii) 512
512 -1 =511
511- 7 = 504
504 – 19 = 485
485 – 37 = 448
448 – 61 = 387
387 – 91 =296
296 – 127 = 169
169 – 169 = 0
∴ 512 = (8)3
∴ Cube root of 512 = 8
(iii) 1728
1728 – 1= 1727
1727 -7 = 1720
1720 -19 = 1701
1701 -37= 1664
1664 – 61 = 1603
1603 – 91 = 1512
1512 -127= 1385 .
1385 – 169= 1216
1216 – 217 = 999
999 – 271 =728
728 – 331 = 397
397 – 397=0
∴ 1728 = (12)3
∴ Cube root of 1728 = 12
Question 2.
Using the method of successive subtraction, examine whether or not the following numbers are perfect cubes :
(i) 130
(ii) 345
(iii) 792
(iv) 1331
Solution:
(i) 130
130 – 1 = 129
129 -7 = 122
122 -19 = 103
103 -37 = 66
66 – 61 = 5
We see that 5 is left
∴ 130 is not a perfect cube.
(ii) 345
345 – 1 = 344
344 – 7 = 337
337 – 19 = 318
318 – 37 = 281
81 – 61 =220
220 – 91 = 129
129 – 127 = 2
We see that 2 is left
∴ 345 is not a perfect cube.
(iii) 792
792 – 1 = 791
791 – 7 = 784
784 – 19 = 765
765 – 37 = 728
728 – 61 = 667
667 – 91 = 576
576 – 127 = 449
449 – 169 = 280
∴ We see 280 is left as 280 <217
∴ 792 is not a perfect cube.
(iv) 1331
1331 – 1 = 1330
1330 -7 = 1323
1323 – 19 = 1304
1304 – 37 = 1267
1267 – 61 = 1206
1206 – 91 = 1115
1115 – 127 = 988
988 – 169 = 819
819 – 217 = 602
602 – 271 = 331
331 – 331 =0
∴ 1331 is a perfect cube
Question 3.
Find the smallest number that must be subtracted from those of the numbers in question 2, which are not perfect cubes, to make them perfect cubes. What are the corresponding cube roots ?
Solution:
We have examined in Question 2, the numbers 130, 345 and 792 are not perfect cubes. Therefore
(i) 130
130 – 1 = 129
129 -7= 122
122 -19 = 103
103 – 37 = 66
66 – 61 = 5
Here 5 is left
∴ 5 < 91 5 is to be subtracted to get a perfect cube.
Cube root of 130 – 5 = 125 is 5
(ii) 345
345 – 1 = 344
344 -7 = 337
337 – 19 = 318
318 – 37 = 281
281 – 61 =220
220 – 91 = 129
129 – 127 = 2
Here 2 is left ∵ 2 < 169
∴ Cube root of 345 – 2 = 343 is 7
∴ 2 is to be subtracted to get a perfect cube.
(iii) 792
792 – 1 = 791
791 – 7 = 784
784 – 19 = 765
765 – 37 = 728
728 – 61 =667
667 – 91 = 576 5
76 – 127 = 449
449 – 169 = 280
280 – 217 = 63
∴ 63 <217
∴ 63 is to be subtracted
∴ Cube root of 792 – 63 = 729 is 9
Question 4.
Find the cube root of each of the following natural numbers :
(i) 343
(ii) 2744
(iii) 4913
(iv) 1728
(v) 35937
(vi) 17576
(vii) 134217728
(viii) 48228544
(ix) 74088000
(x) 157464
(xi) 1157625
(xii) 33698267
Solution:
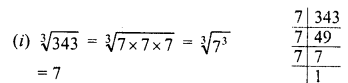
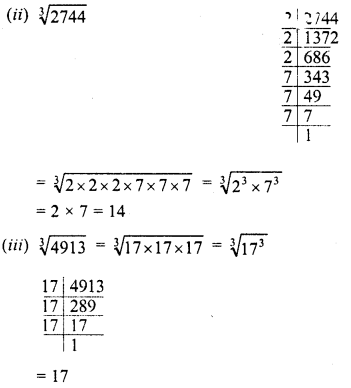
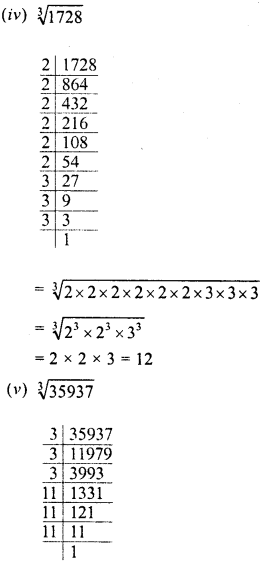







Question 5.
Find the smallest number which when multiplied with 3600 will make the product a perfect cube. Further, find the cube root of the product.
Solution:
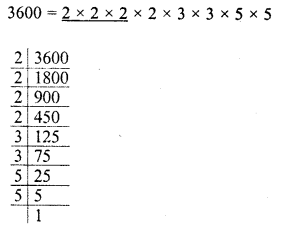
Grouping the factors in triplets of equal factors, we see that 2, 3 x 3 and 5 x 5 are left
∴ In order to complete the triplets, we have to multiply it by 2, 3 and 5.
∴ The smallest number to be multiplied = 2×2 x 3 x 5 = 60
Now product = 3600 x 60 = 216000 and cube root of 216000
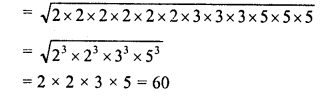
Question 6.
Multiply 210125 by the smallest number so that the product is a perfect cube. Also, find out the cube root of the product.
Solution:

Grouping the factors in triplets of equal factors, we see that 41 x 41 is left
∴ In order to complete the triplet, we have to multiply it by 41
∴ Smallest number to be multiplied = 41
∴ Product = 210125 x 41 = 8615125
∴ Cube root of 8615125
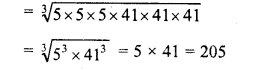
Question 7.
What is the smallest number by which 8192 must be divided so that quotient is a perfect cube ? Also, find the cube root of the quotient so obtained.
Solution:

Grouping the factors in triplets of equal factors, we see that 2 is left
∴ Dividing by 2, we get the quotient a perfect cube
∴ Perfect cube = 8192 + 2 = 4096
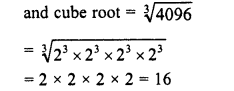
Question 8.
Three numbers are in the ratio 1:2:3. The sum of their cubes is 98784. Find the numbers.
Solution:
Ratio in numbers =1:2:3
Let first number = x
Then second number = 2x
and third number = 3x
∴ Sum of cubes of there numbers = (x)3 + (2x)3+(3x)3
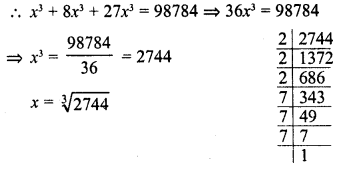
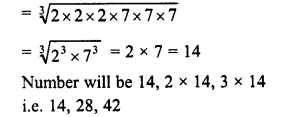
Question 9.
The volume of a cube is 9261000 m3. Find the side of the cube.
Solution:

Hope given RD Sharma Class 8 Solutions Chapter 4 Cubes and Cube Roots Ex 4.3 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.