RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1
These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1
Other Exercises
- RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1
- RD Sharma Class 10 Solutions Chapter 12 Heights and Distances VSAQS
- RD Sharma Class 10 Solutions Chapter 12 Heights and Distances MCQS
Question 1.
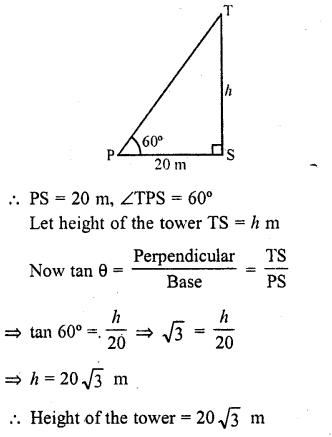
A tower stands vertically on the ground. From a point on the ground, 20 m away from the foot of the tower, the angle of elevation of the top of the tower is 60°. What is the height of the tower ?
Solution:
Let TS is the tower and P is a point which is 20 m away from the foot of the tower and angle of elevation of T is 60°
Question 2.
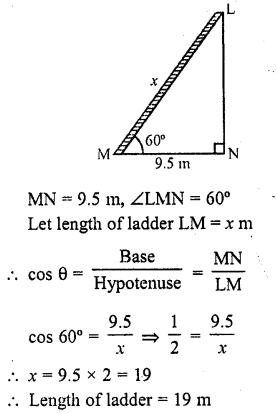
The angle of elevation of a ladder leaning against a wall is 60° and the foot of the ladder is 9.5 m away from the wall. Find the length of the ladder.
Solution:
Let LM is the ladder which makes an angle of 60° with the wall LM
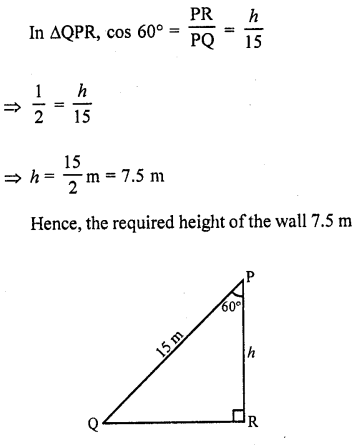
Question 3.
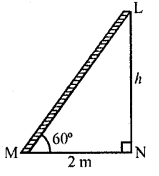
A ladder is placed along a wall of a house such that its upper end is touching the top of the wall. The foot of the ladder is 2 m away from the wail and the ladder is making an angle of 60° with the level of the ground. Determine the height of the wall.
Solution:
Let LM be the ladder which makes an angle of 60° with the wall LN and at a distance of 2 m from the foot of the wall

Question 4.
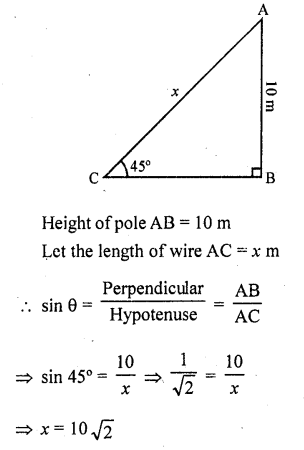
An electric pole is 10 m high. A steel wire tied to top of the pole is affixed at a point on the ground to keep the pole up right. If the wire makes an angle of 45° with the horizontal through the foot of the pole, find the length of the wire.
Solution:
Let AB be the pole and a wire AC is tied to the top of the pole with a point C on the ground which makes an angle of 45° with the ground
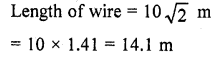
Question 5.
A kite is flying at a height of 75 metres from the ground level, attached to a string inclined at 60° to the horizontal. Find the length of the string to the nearest metre.
Solution:
Let K be the kite flying in the sky at a height of 75 m from the ground LM. The string KL makes an angle of 60° to the ground
Let length of string KL = x m
KM = 75 m
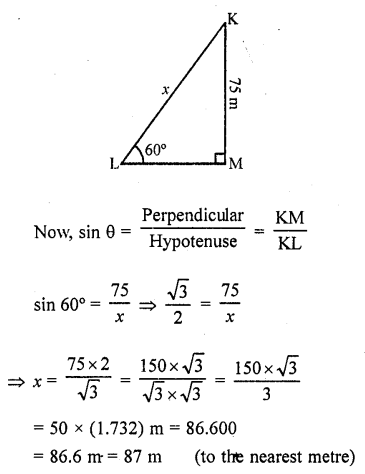
Question 6.
A ladder 15 m long just reaches the top of a vertical wall. If the ladders makes an angle of 60° with the wall, then find the height of the wall.
Solution:
Given that, the height of the ladder = 15 m
Let the height of the vertical wall = h
and the ladder makes an angle of elevation 60° with the wall i.e., θ = 60°.
Question 7.
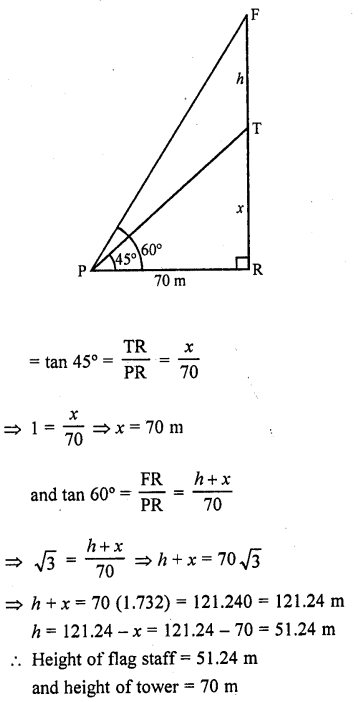
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag-staff. At a point on the plane 70 metres away from the tower, an observer notices that the angles of elevation of the top and the bottom of the flag-staff are respectively 60° and 45°. Find the height of the flag-staff and that of the tower.
Solution:
Let TR be the tower and FT is the flag on it. P is an point on the ground 70 m away from the foot of the tower. From P, the angle of elevation of the top and bottom of the flag are 60° and 45° respectively Let h be the height of flag staff and x be the height of the tower
Question 8.
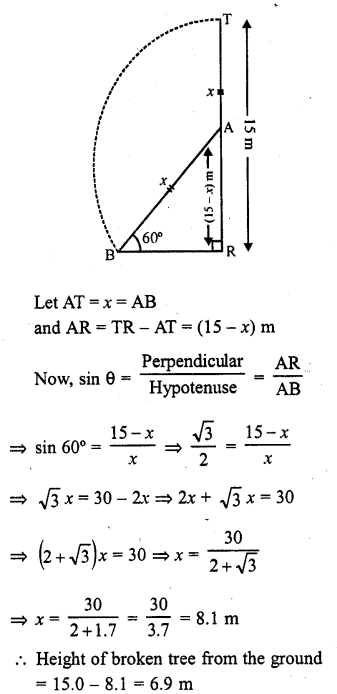
A vertically straight tree, 15 m high, is broken by the wind in such a way that its top just touches the ground and makes an angle of 60° with the ground. At what height from the ground did the tree break ? [CBSE 1995]
Solution:
Let TR be the tree whose height is 15 m
Let it is broken from A and its top T touches the ground at B making an angle of 60° with the ground
Question 9.
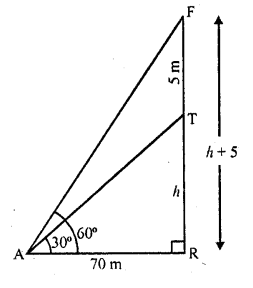
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag-staff of height 5 metres. At a point on the plane, the angles of elevation of the bottom and the top of the flag-staff are respectively 30° and 60°. Find the height of the tower. (C.B.S.E. 1995)
Solution:
Let TR be the tower and FT is a flag staff on it. A is a point on the ground such that it makes angles of elevation of the bottom and top of the flag staff of 30° and 60° respectively

Question 10.
A person observed the angle of elevation of the top of a tower as 30°. He walked 50 m towards the root of the tower along level ground and found the angle of elevation of the top of the tower as 60°. Find the height of the tower.
Solution:
Let TR be the tower. A person at A on the ground observes the angle of elevation of the top T of the tower as 30° and then moves towards the foot of the tower. At a distance of 50 m at B, the angle of elevation becomes 60°
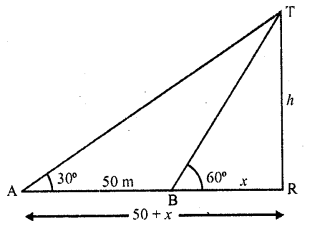
Let h be the height of the tower and BR = x, then AR = (50 + x)

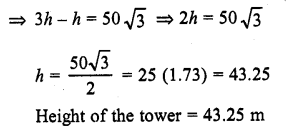
Question 11.
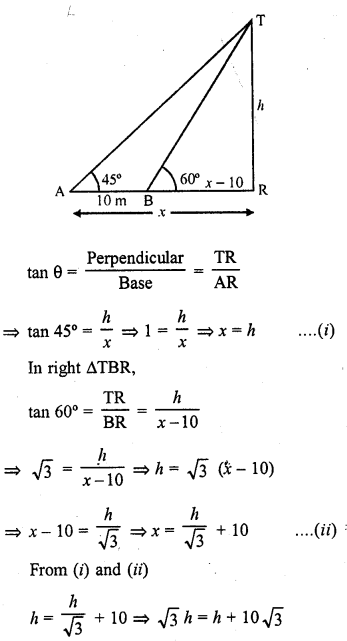
The shadow of a tower, when the angle of elevation of the sun is 45°, is found to be 10 m longer than when it was 60°. Find the height of the tower.
Solution:
Let TR be we know
Let the shadow of TR at the elevation of the sun 45° be x m and at 60°, will be (x – 10) m Now in right ΔTAR,
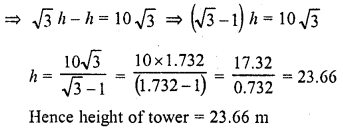
Question 12.
A parachutist is descending vertically and makes angles of elevation of 45° and 60° at two observing points 100 m apart from each other on the left side of himself. Find the maximum height from which he falls and the distance of the point where he falls on the ground from the just observation point.
Solution:
Let P be the parachutist landing to Q on the ground
A and B are two observations such that AB = 10 m
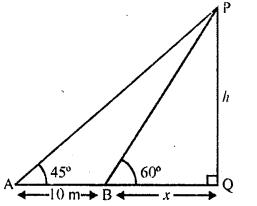
Let h be the height of the parachutist from the ground and x be the distance of B from Q and (100 + x) is the distance from A to Q Now in right ΔAPQ,

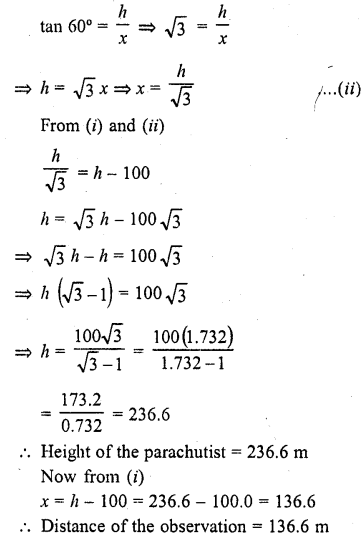
Question 13.
On the same side of a tower, two objects are located. When observed from the top of the tower, their angles of depression are 45° and 60°. If the height of the tower is 150 m, find the distance between the objects. (C.B.S.E. 1992)
Solution:
Let TR be the tower and A, B are two objects which makes angles of elevation with top of the tower as 45° and 60° respectively
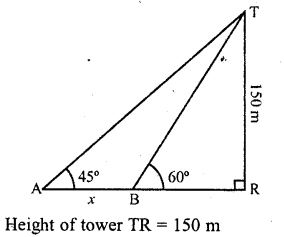

Question 14.
The angle of elevation of a tower from a point on the same level as the foot of the tower is 30°. On advancing 150 metres towards the foot of the tower, the angle of elevation of the tower becomes 60°. Show that the height of the tower is 129.9 metres (Use\(\sqrt { 3 } \) = 1-732). (C.B.S.E. 2006)
Solution:
Let TR be the tower. A is a point on the same level which makes an angle of elevation of 30° with the top of the tower TR, and 150 m from A towards the foot of the tower the angle of elevaton is 60°, Let TR = h m
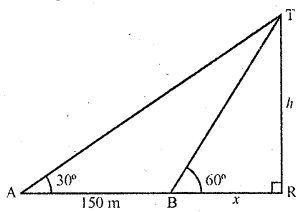

Question 15.
The angle of elevation of the top of a tower as observed from a point in a horizontal plane through the foot of the tower is 32°. When the observer moves towards the tower a distance of 100 m, he finds the angle of elevation of the top to be 63°. Find the height of the tower and the distance of the first position from the tower. [Take tan 32° = 0.6248 and tan 63° = 1.9626] (C.B.S.E. 2001C)
Solution:
Let PQ be the tower and from a points A, and B the angles of elevations of top P of the tower are 32° and 63° respectively and AB= 100 m


Question 16.
The angle of elevation of the top of a tower from a point A on the ground is 30°. On moving a distance of 20 metres towards the foot of the tower to a point B the angle of elevation increases to 60°. Find the height of the tower and the distance of the tower from the point A. (C.B.S.E. 2002)
Solution:
Let CD be the tower and from a point A on the same ground, the angle of elevation of the top of the tower is 30°. B is another point such that AB = 20 m and from B, the angle of elevation is 60°
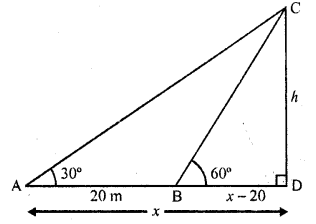
Let h be the height of the tower CD and x is the length of AD
∴ BD = (x – 20) m
Now in right ΔCAD

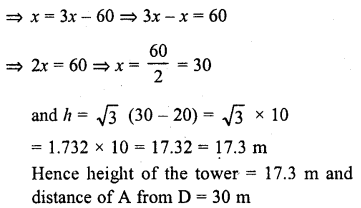
Question 17.
From the top of a building 15 m high the angle of elevation of the top of a tower is found to be 30°. From the bottom of the same building, the angle of elevation of the top of the tower is found to be 60°. Find the height of the tower and the distance between the tower and building. (C.B.S.E. 2002)
Solution:
Let TR be the tower and AB be the building The angles of elevation of the top of the tower T, from A is 30° and from B is 60°
Height of AB = 15 m
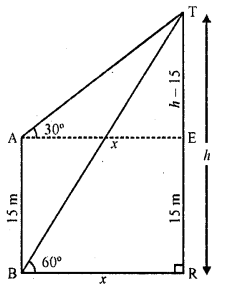
Let the height of tower TR = h and the distance between the tower and building = x
In right ΔTBR,
![]()

Question 18.
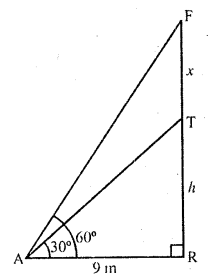
On a horizontral plane there is a vertical tower with the flag pole on the top of the tower. At a point 9 metres away from the foot of the tower the angle of elevation of the top and bottom of the flag pole are 60° and 30° respectively. Find the height of the tower and the flag pole mounted on it. (C.B.S.E. 2005)
Solution:
Let TR be the tower and F is the flag pole on it. A is a point 9 m away from the foot of the tower and angles of elevation of the top and bottom of the flag pole from A are 60° and 30° respectively
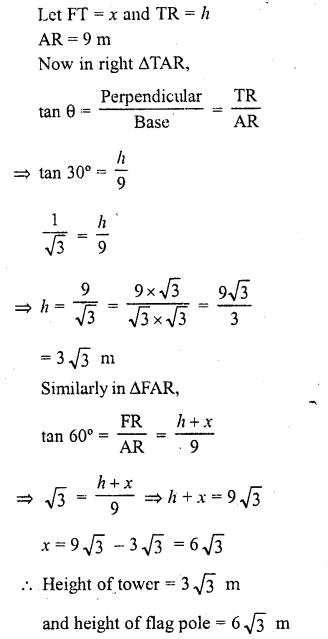
Question 19.
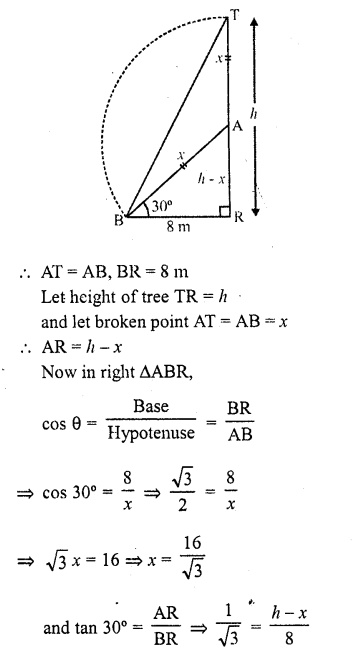
A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle of 30° with the ground. The distance between the foot of the tree to the point where the top touches the ground is 8 in. Find the height of the tree.
Solution:
Let TR be the tree and it is broken from A and broken part of the tree makes an angle of 30° on the ground at B
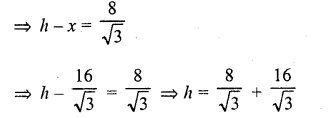
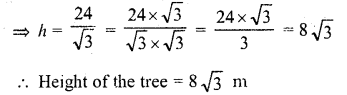
Question 20.
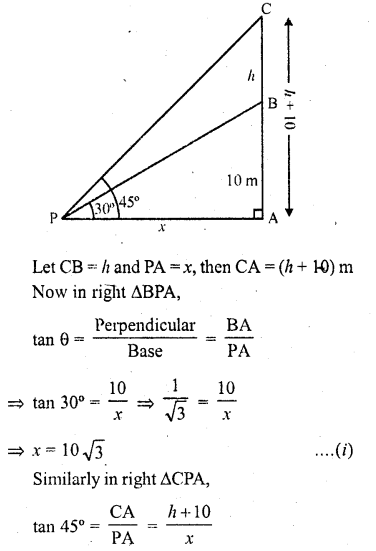
From a point P on the ground the angle of elevation of a 10 m tall building is 30°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flag-staff from P is 45°. Find the length of the flag-staff and the distance of the building from the point P. (Take \(\sqrt { 3 } \) = 1.732
Solution:
Let BA is the building such that BA = 10 in CB is a flag-staff on the building P is a point on the ground such that the angles of the elevation of the top of the building is 30° and that of the top of the flag-staff is 45°
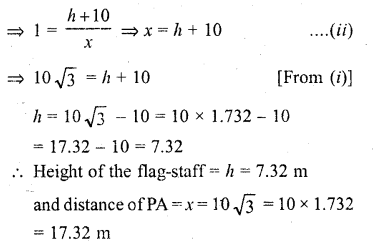
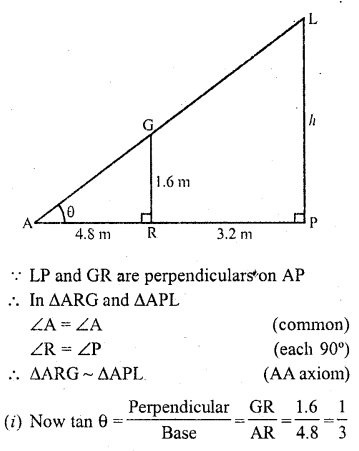
Question 21.
A 1.6 m tall girl stands at a distance of 3.2 m from a lamp-post and casts a shadow of 4.8 m on the ground. Find the height of the lamp-post by using
(i) trigonometric ratios
(ii) property of similar triangles.
Solution:
Let LP is the lamp-post and GR is the girl who is at a distance of 3.2 m
From the lamp-post and its shadow is AR which is 4.8 m long. Let ∠A = 0
Height of girl GR = 1.6 m and let height of lamp post = h

Question 22.
A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increasees from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.
Solution:
Let BA is the boy whose height is 1.5 m and CD is building whose height is 30 m Angle of elevation of C from B (eyes of the boy) is 30°
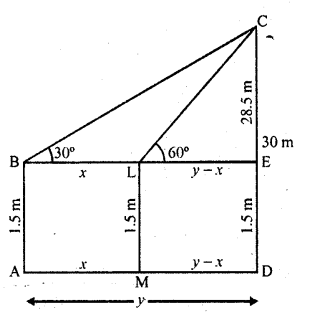
and on moving some distance towards the building at L, the angle of elevation of C is 60°
Let AM = BL = x and AD = y
Then LE = MD = y – x
and CE = CD – ED = 30 – 1.5 = 28.5 m
Now in right ΔCBE

Question 23.
The shadow of a tower standing on a level ground is found to be 40 m longer when Sun’s altitude is 30° than when it was “60°. Find the height of the tower.
Solution:
Let TR be the tower and RB and RA are its shadows at the elevation of 60° and 30° respectively. Such that BA = 40 m
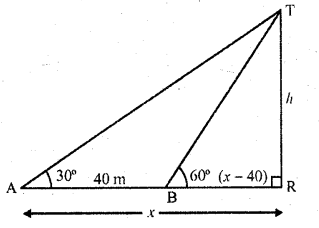
Let h be the height of the tower and let shadow RA = x m
Then shadow RB = (x – 40) m
Now in right ΔTAR,
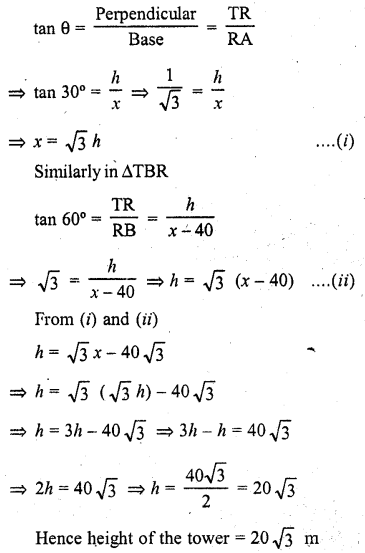
Question 24.
From a point on the ground the angles of elevation of the bottom and top of a transmission tower fixed at the top of 20 m high building are 45° and 60° respectively. Find the height of the transmission tower.
Solution:
BC is the building and AB is the transmission on it the height of the building is 20 m From a point P, the angles of elevation of B and A are 45° and 60° respectively
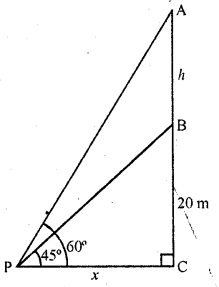
Let height of the transmission AB = h and let PC = x
Now in right ΔBPC,

Question 25.
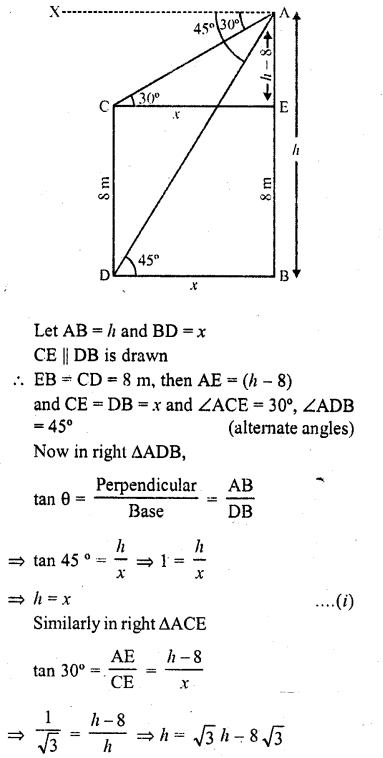
The angles of depression of the top and bottom of 8 m tali building from the top of a multistoried building are 30° and 45° respectively. Find the height of the multistoried building and the distance Between the two buildings.
Solution:
Let AB be the multistoried building and CD is another building. From A, the angles of depression of the top C and bottom D of the other building are 30° and 45° respectively Height of building is 8 m i.e. CD = 8 m
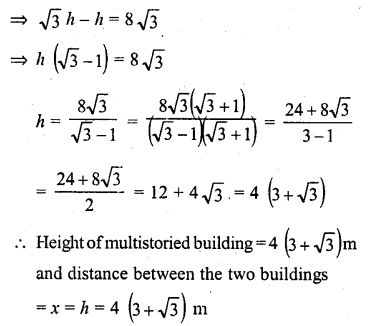
Question 26.
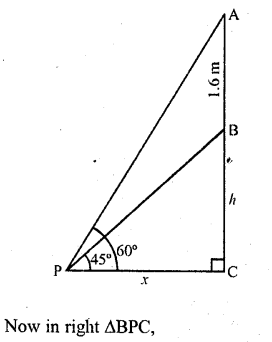
A statue 1.6 m tall stands on the top of pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point the angles of elevation of the top of thd\pedestal is 45°. Find the height of the pedestal. (C.B.S.E. 2008)
Solution:
Let AB be the statue standing on the top of a pedestal BC
From a point P on the ground the angles of elevation of the top of the statue is 60° and top of the pedestal BC is 45°
Let height of BC = h and PC = x
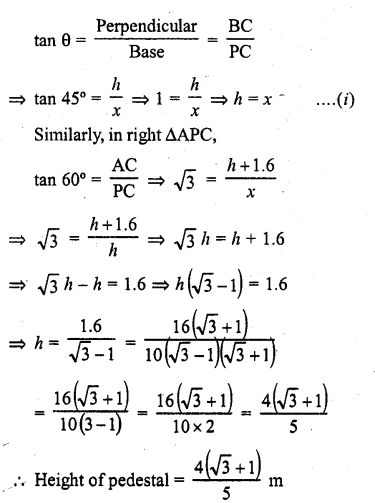
Question 27.
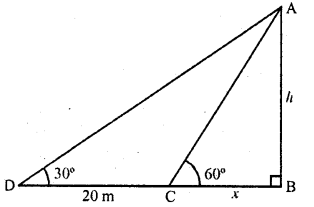
A T.V. Tower stands vertically on a bank of a river. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From a point 20 m away this point on the same bank, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the river.
Solution:
Let AB is the T.V. tower and CB is the,width of the river. D is a point which is 20 m away from C
Now angles of elevation from A to C and D are 60° and 30° respectively.
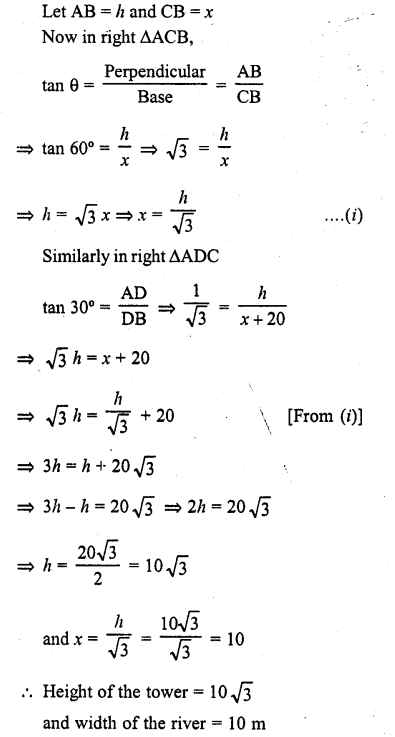
Question 28.
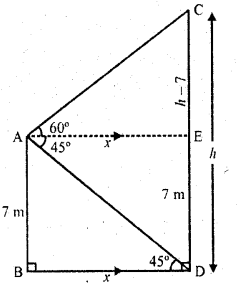
From the top of a 7 m high building, the – angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
Solution:
Let AB be the building and CD be the cable tower
From the top of building, the angle of elevation of the top of tower is 60° and angle of depression of the foot of the tower is 45° Now AB = 7 m

Question 29.
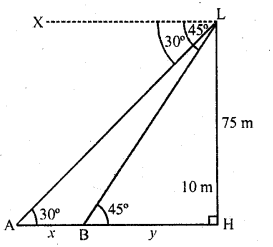
As observed from the top of a 75 m tall lighthouse, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
Solution:
Let LH is die light house and A, B are two ships From L, angles of depression of the ships A and B are 30° and 45° respectively

Question 30.
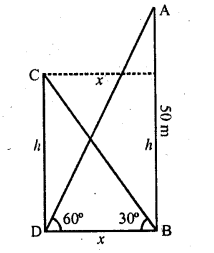
The angle of elevation of the top of the building from the foot of the tower is 30° and the angle of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.
Solution:
Let AB be the tower and CD is the building The angle of elevation of the top of the building from the foot of the tower is 30° and the angle of the top of the tower from the foot of the building is 60°

Question 31.
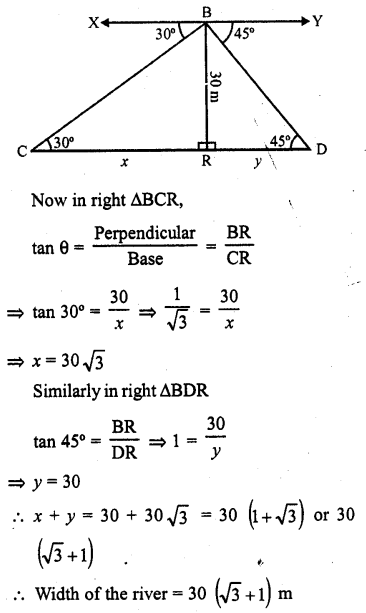
From a point on a bridge across a river the angles of depression of the banks onopposite side of the river are 30° and 45° respectively. If bridge is at the height of 30 m from the banks, find the width of the river.
Solution:
Let BR is the bridge with a height of 30 m and angles of depression from B the top of the bridge to two given points C and D on the opposite sides of the river are 30° and 45° respectively CD is the width of the river Let CR = x and DR = y
Question 32.
Two poles of equal heights are standing opposite to each other on either side of the road which is 80 m wide. From a point between them on the road the angles of elevation of the top of the poles are 60° and 30° respectively. Find the height of the poles and the distances of the point from the poles.
Solution:
AB and CD are two equal poles on either side of the road BD which is 80 m wide P is a point on the road such that the angles of elevation of the tops of the poles are 60° and 30° respectively
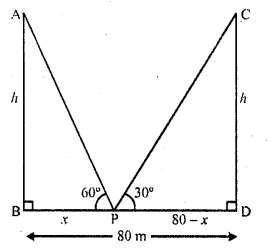
Let the length of each pole in h and let BP = x, then DP = 80 – x
In right ΔABP,

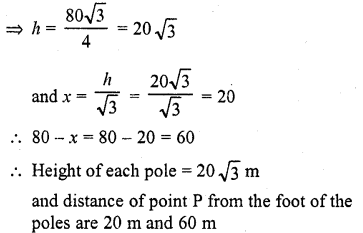
Question 33.
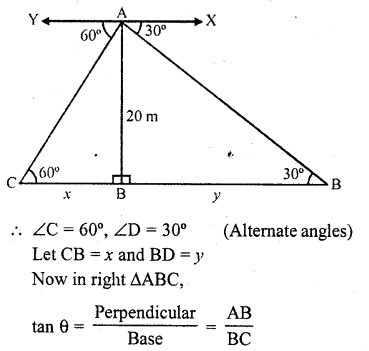
A man sitting at a height of 20 m on a tall tree on a small island in the middle of a river observes two poles directly opposite to each other on the two banks of the river and in line with the foot of tree. If the angles of depression of the feet of the poles from a point at which the man is sitting on the tree on either side of the river are 60° and 30° respectively. Find the width of the river.
Solution:
Let AB be the tree on which a man is sitting the tree is on a small island in the middle of the river. C and D are the foot of the poles on either bank of the river The angles of depression from A to the poles C and D are 60° and 30° respectively and AB = 20 m

Question 34.
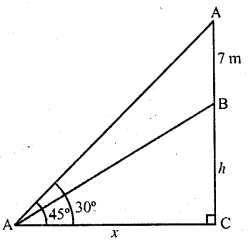
A vertical tower stands on a horizontal plane and is surmounted by a flag-staff of height 7 m. From a point on the plane, the angle of elevation of the bottom of the flag-staff is 30° and that of the top of the flag-staff is 45°. Find the height of the tower.
Solution:
Let AB be a flag post on a building BC From a point P on the same ground, angle of elevations of A and B are 45° and 30° respectively
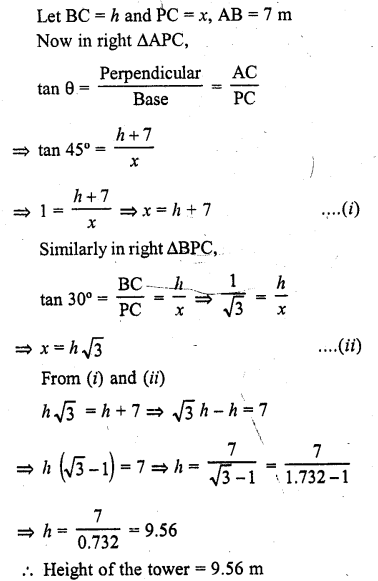
Question 35.
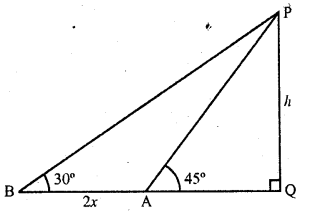
The length of the shadow of a tower standing on level plane is found to be 2x metres longer when the sun’s altitude is 30° than when it was 45°. Prove that the height of tower is x (\(\sqrt { 3 } \) +1) metres.
Solution:
Let PQ be the tower whose shadow is QA at the elevation of 45° and QB at the elevation of 30° such that AB = 2x

Question 36.
A tree breaks due to the storm and the broken part bends so that the top of the tree touches the ground making an angle of 30° with the ground. The distance from the foot of the tree to the point where the top touches the ground is 10 Find the height of the tree.
Solution:
Let TR be the tree arid it is broken at S and its broken parts touches the ground at P making ah angle of 30° elevation angle,
PR = 10 m
Let length of the tree TR = h and let TS = SP = x
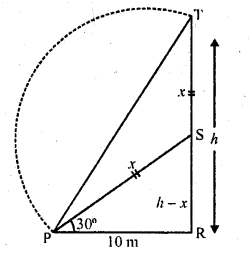
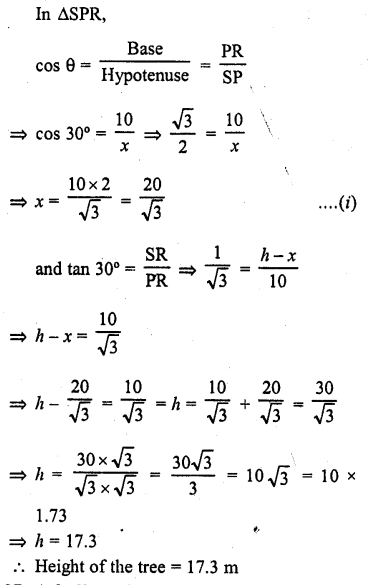
Question 37.
A balloon is connected to a meteorological ground station by a cable of length 215 m inclined at 60° to the horizontal. Determine the height of the balloon from the ground. Assume that there is no slack in the cable.
Solution:
Let B is the balloon which is connected by the cable BC which is 215 m long and makes an angle of elevation of 60° with the ground Let h be the height of the balloon
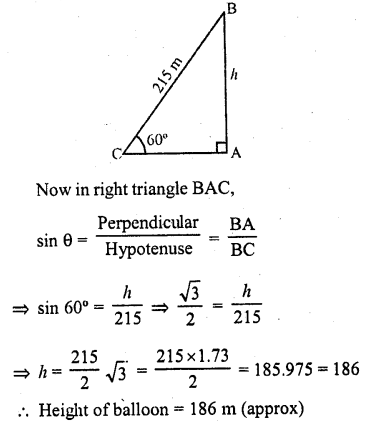
Question 38.
Two men on either side of the cliff 80 m high observes the angles of elevation of the top of the cliff to be 30° and 60° respectively. Find the distance between the two men.
Solution:
Let CL is the cliff and A and B are two men on either side of the cliff making angles of elevation with C as 30“ and 60“ respectively Height of cliff CL = 80 m
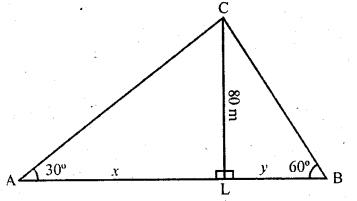

Question 39.
Find the angle of elevation of the sun (sun’s altitutde) when the length of the shadow of a vertical pole is equal to its height.
Solution:
Let the height of pole AB = h m
Then its shadow = h m

Question 40.
An aeroplane is flying at a height of 210 m. Flying at this height at some instant the angles of depression of two points in a line in opposite directions on both the banks of the river are 45° and 60°. Find the width of the river. (Use \(\sqrt { 3 } \) = 1.73) [CBSE 2015]
Solution:
Height of the aeroplane = 210 m
Let AB is the height of aeroplane and C and D are the points on the opposite banks of a river.
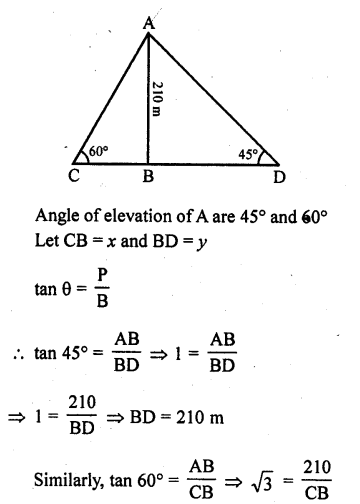
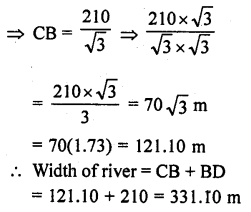
Question 41.
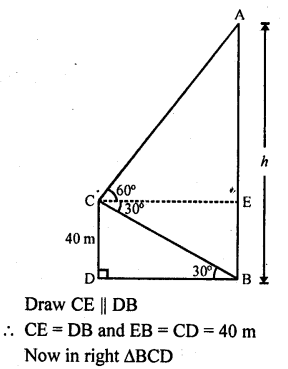
The angle of elevation of the top of a chimney from the top of a tower is 60° and the angle of depression of the foot of the chimney from the top of the tower is 30°. If the height of the tower is 40 m, find the height of the chimney. According to pollution control norms, the minimum height of a smoke emitting chimney should be 100 m. State if the height of the above mentioned chimriey meets the pollution norms. What value is discussed in this question? [CBSE 2014]
Solution:
Let CD be the tower area AB be the chimney angle of elevation of the top of tower with the top of the chimney is 60° and foot of chimney with the top of tower is 30°
CD = 40 m
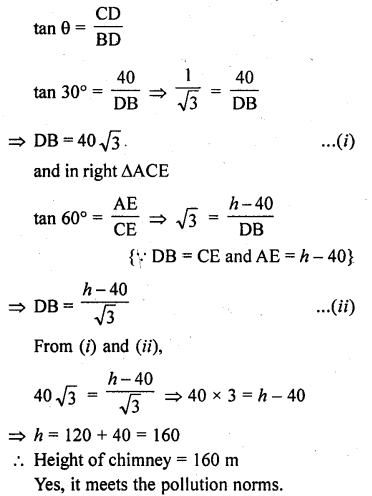
Question 42.
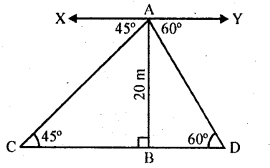
Two ships are there in the sea on either side of a light house in such a way that the ships and the light house are in the same straight line. The angle of depression of two ships are observed from the top of the light house are 60° and 45° respectively. If the height of the light house is 200 m, find the distance between the two ships. (Use \(\sqrt { 3 } \) = 1.73)
Solution:
Let AB be the light house and C and D are two ships which make angle of depression with the top A of the light house of 60° and 45°
AB = 20 m

Question 43.
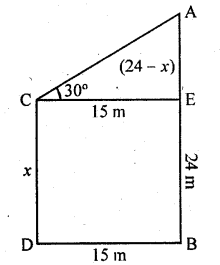
The horizontal distance between two poles is 15 m. The angle of depression of the top of the first pole as seen from the top of the second pole is 30°. If the height of the second pole is 24 m, find the height of the first pole. (\(\sqrt { 3 } \) = 1.732) [CBSE 2013]
Solution:
Let AB and CD are two poles and distance between them = 15 m, and AB = 24 m Angle of elevation from top of pole CD, to pole AB = 30°
From C, draw CE || DB
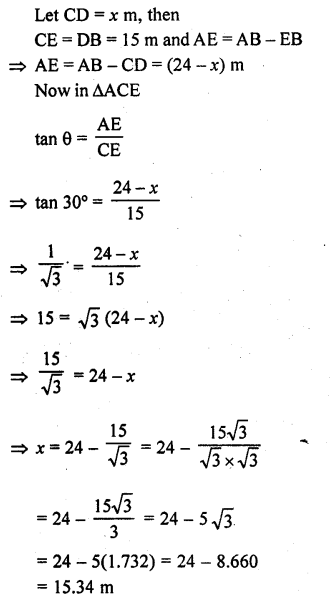
Question 44.
The angles of depression of two ships from the top of a light house and on the same side of it are found to be 45° and 30° respectively. If the ships are 200 m apart, find the height of the light house.
Solution:
Let PQ be the light house and A and B are two ships on the same side of the light house Angle of depression from top of the light house of the two ships are 30° and 45°
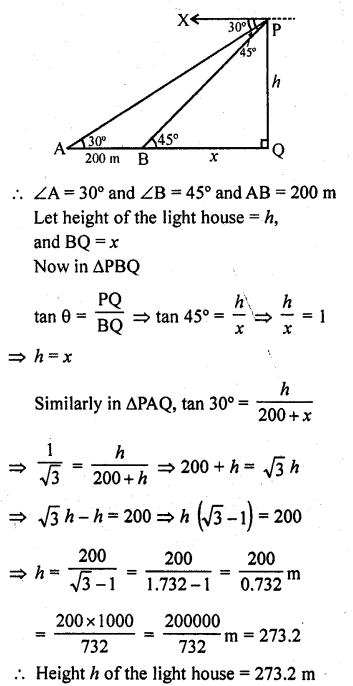
Question 45.
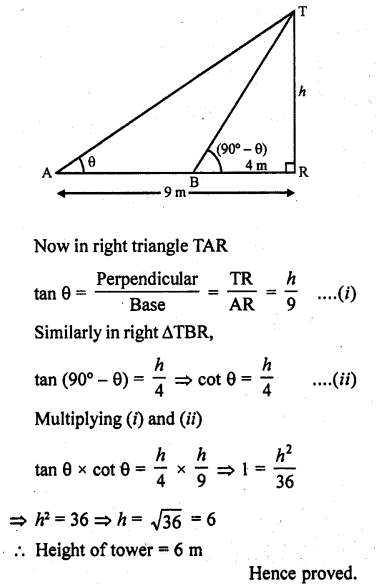
The angles of elevation of the top of a tower from two points at’a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
Solution:
Let TR be the tower. A and B are two points which make the angled of elevation with top of tower as θ and 90° – θ (∵ angles are complementary)
Let height of tower TR = h and AR = 9 m, BR = 4m
Question 46.
From the top of a 50 m high tower, the angles of depression of the top and bottom of a pole are observed to be 45° and 60° respectively. Find the height of the pole.
Solution:
Let AB be the tower and CD is the pole. Angles of depression from the top A to the top and bottom of the pole are 45° and 60° respectively
AB = 50 m, let CD = h and BD = EC = x
∵ CE || DB
∴ EB = CD = h
and AE = 50 – h
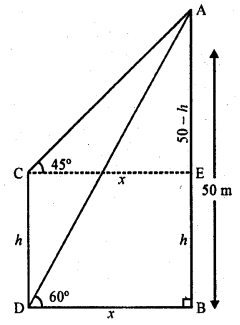

Question 47.
The horizontal distance between two trees of different heights is 60 m. The angle of depression of the top of the first tree when seen from the top of the second tree is 45°. If the height of the second tree is 80 m, find the height of the first tree.
Solution:
Let AB and CD be the two trees
AB = 80 m, angle of depression from A of C is 45°. Draw CE || DB
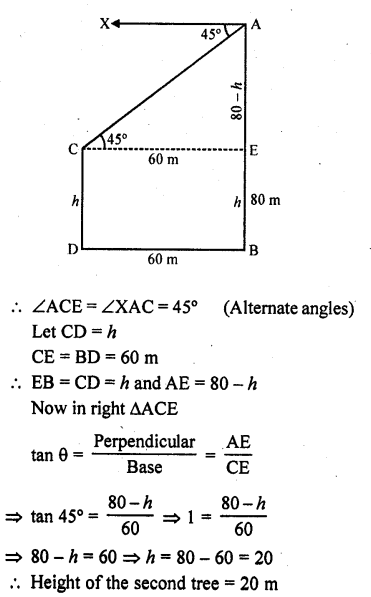
Question 48.
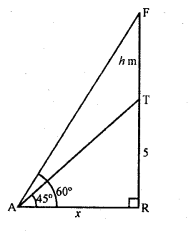
A flag-staff stands on the top of a^5 m high tower. From a point on the ground, the angle of elevation of the top of the flag-staff is 60° and from the same point, the angle of elevation of the top of the tower is 45°. Find the height of the flagstaff.
Solution:
Let FT is the flag-staff situated on the top of the tower TR. A is any point on the same plane which makes angles of elevation with top of the flag-staff and top of the tower are 60° and 45° respectively.

Use Cuemath’s Online Kilometer To Mile Calculator and convert kilometers to miles in just one click.
Question 49.
The angle of elevation of the top of a vertical tower PQ from a point X on the ground is 60°. At a point Y, 40 m vertically above X, the angle of elevation of the top is 45°. Calculate the height of the tower.
Solution:
Let TR is the tower From a point X, the angle of elevation of T is 60° and 40 m above X, from the point Y, the angle of elevation is 45°
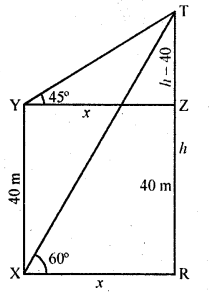

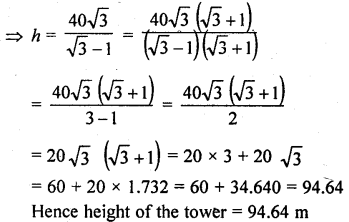
Question 50.
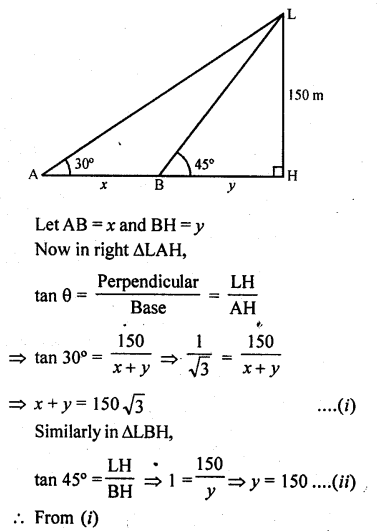
As observed from the top of a 150 m tall light house, the angles of depression of two ships approaching it are 30° and 45°. If one ship is directly behind the other, find the distance between the two ships.
Solution:
Let LH be the light house, A apd B ate two ships making angles of elevation with the top of the light house as 30° and 45° respectively.
LH = 150 m.
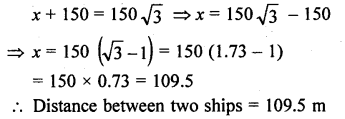
Question 51.
The angles of elevation of the top of a rock from the top and foot of a 100 m high tower are respectively 30° and 45°. Find the height of the rock.
Solution:
Let RS is the rock and TP is the tower. The angles of elevation of the top of rock with the top and foot of the tower are 30° and 45° respectively
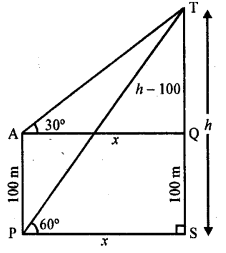
Height of TP = 100 m
Let height of rock RS = h
From T, draw TQ || PS _
Then QS = TP = 100 m ‘
and RQ = h – 100
Let PS = TQ = x
Now in right ΔRPS

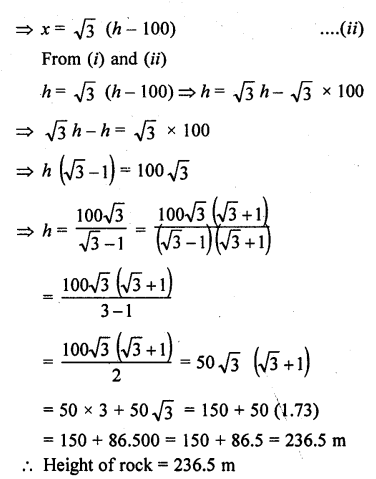
Question 52.
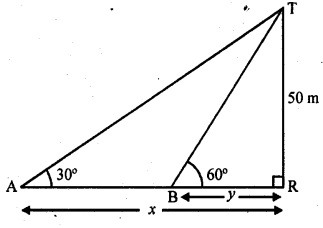
A straight highway leads to the foot of a tower of height 50 m. From the top of the tower, the angles of depression of two cars standing on the highway are 30° and 60° respectively. What is the distance between the two cars and how far is each car from the tower ?
Solution:
Let TR be the tower and A and B are two cars on the road making angles of elevation with T the top of tower as 30° and 60°
Height of the tower TR = 50 m
Let AR = x and BR = y
Now in right ΔTAR,

Question 53.
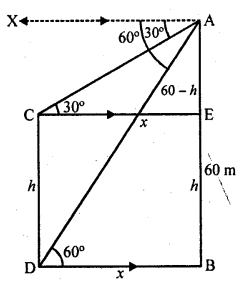
From the top of a building AB, 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find
(i) the horizontal distance between AB and CD.
(ii) the height of the lamp post
(iii) the difference between the heights of the building and the lamp post. [CBSE 2009]
Solution:
Let AB is the building and CD is the verticle lamp
From A, the top of the building angles of depression of C and D are 30° and 60° respectively
Height of building AB = 60 m
Let height of CD = h
Draw CE || DB || AX
∴ ∠ACE = ∠XAC = 30° and ∠ADB = ∠XAD = 60°
EB = CD = h and AE = 60 – h
Let DB = CE = x
Now in right ΔACE,


Question 54.
Two boats approach a light house in midsea from opposite directions. The angles of elevation of the top of the light house from two boats are 30° and 45° respectively. If the distance between two boats is 100 m, find the height of the light house. [CBSE 2014]
Solution:
Let LH is the light house and A and B are two boats on the opposite directions of the light house which are making angle of elevation of the top L of the light house as 30° and 45°
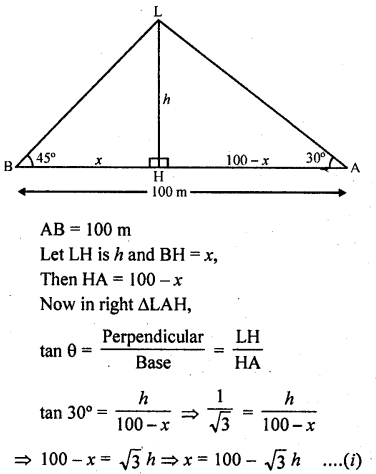
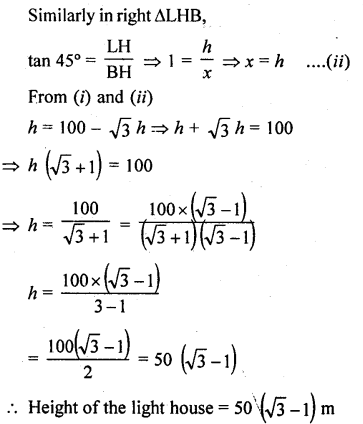
Question 55.
The angle of elevation of the top of a hill at the foot of a tower is 60° and the angle of elevation of the top of the tower from the foot of the hill is 30°. If the tower is 50 m high, what is the height of the hill ?[CBSE 2006C, 2013]
Solution:
Let TR be the tower, HL is the hill and angles of elevation of top of the hill is 60° and top of the tower is 30
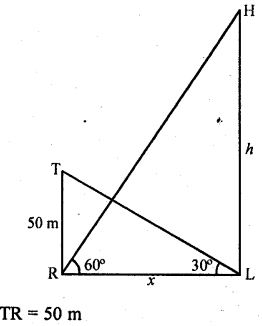

Question 56.
A moving boat is observed from the top of a 150 m high cliff moving away from the cliff. The angle of depression of the boat changes from 60° to 45° in 2 minutes. Find the speed of the boat in m/h. [CBSE 2017]
Solution:
Let the distance BC be x m and CD be y m.
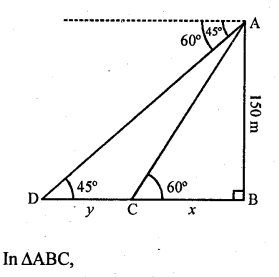
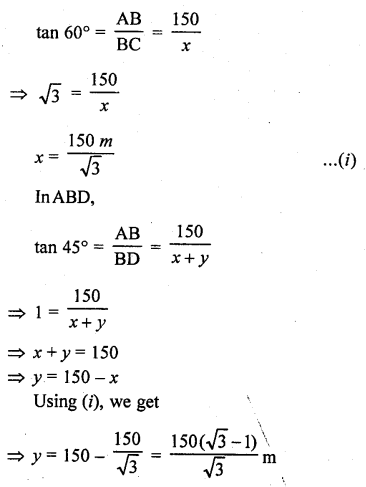

Question 57.
From the fop of a 120 m ifigh tower, a man observes two cars on the opposite sides of the tower and in straightline with the base of tower with angles of depression as 60° and 45°. Find the distance between the cars. (Take \(\sqrt { 3 } \) = 1.732) [CBSE 2017]
Solution:
Let BD be the tower and A and C be the two points on ground.
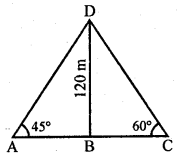
Then, BD, the height of the tower = 120m
∠BAD = 45°, ∠BCD = 60°

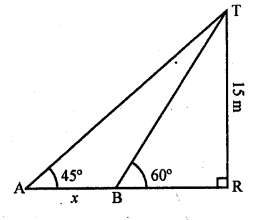
Question 58.
Two points A and B are on the same side of a tower and in the same straight line with its base. The angles of depression of these points from the top of the tower are 60° and 45° respectively. If the height of the tower is 15 m, then find the distance between these points. [CBSE2017]
Solution:
Let TR be the tower and A, B are two objects which makes angles of elevation with top of the tower as 45° and 60° respectively


Question 59.
A fire in a building B is reported on telephone to two fire stations P and Q, 20 km apart from each other on a straight road. P observes that the fire is at an angle of 60° to the road and Q observes that it is at an angle of 45° to the road. Which station should send its team and how much will this team have to travel ?
Solution:
Let B is the building one fire and P and Q the fire stations which are 20 km apart i.e., PQ = 20 km.
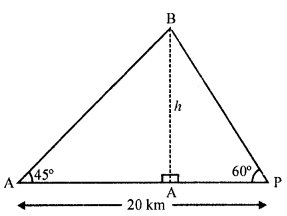
P and Q observes the angles with B, as 60° and 45° respectively.
Draw BA ⊥ PQ
Let AB = h Now in right ΔBAQ

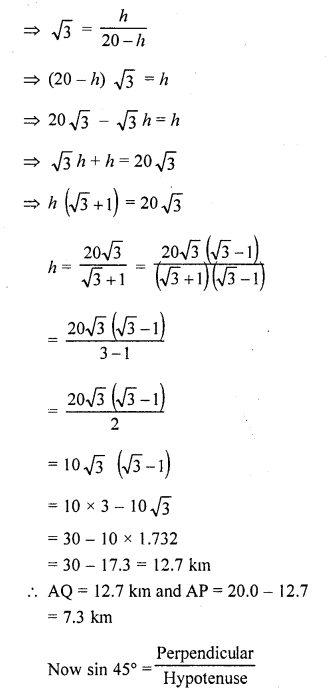


Question 60.
A man on the deck of a ship is 10 m above the water level. He observes that the angle of elevation of the top of a cliff is 45° and the angle of depression of the base is 30°. Calculate the distance of the cliff from the ship and the height of the cliff.
Solution:
Let M is a man on the deck MN such that MN = 10 m, AB is the cliff
From M the angle of elevation of A is 45°
and angle of depression of B is 30°
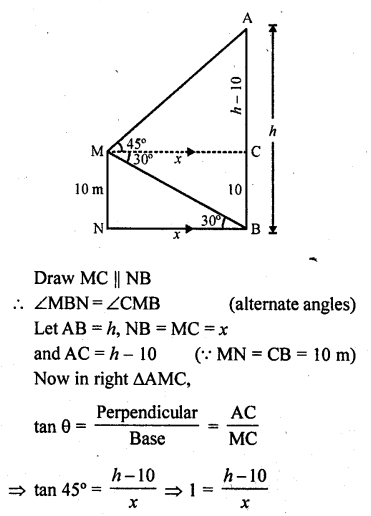

Question 61.
A man standing on the deck of a ship, which is 8 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill.
Solution:
Let M is the man on the deck MN such that MN = 8 m. AB is the hill From M, the angle of elevation of A is 60° and angle of depression of B is 30°
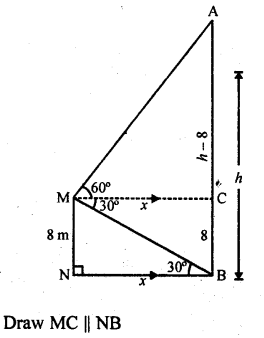

Question 62.
There are two temples, one on each bank of a river, just opposite to each other. One temple is 50 m high. From the top of this temple, the angles of depression of the top and the foot of the other temple are 30° and 60° respectively. Find the width of the river and the height of the other temple.
Solution:
Let AB and CD are two temples on the banks of the river.
AB = 50 m
From A, the angles of depression of the top and botttom of the other temple are 30° and 60° respectively.
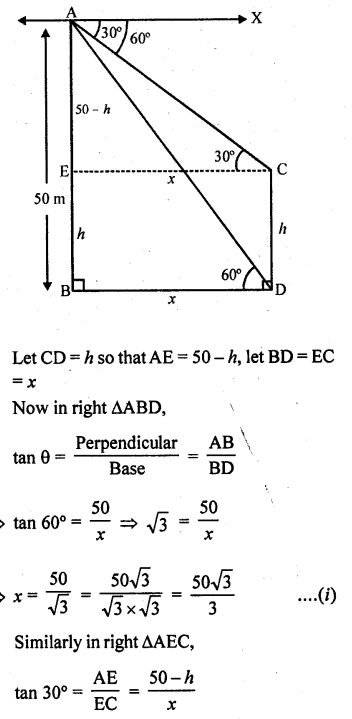
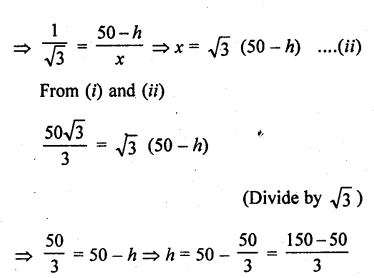

Question 63.
The angle of elevation of an aeroplane from a point on the ground is 45°. After a flight of 15 seconds, the elevation changes to 30°. If the aeroplane is flying at a height of 3000 metres, find the speed of the aeroplane.
Solution:
Let A is the plane flying in the sky at is height of 3000 m i.e., AB = 3000 m
P is a point on the ground which from an angle of elevation of 45° at A and then after a flight of 15 seconds at A’ the angle of elevation because 30°
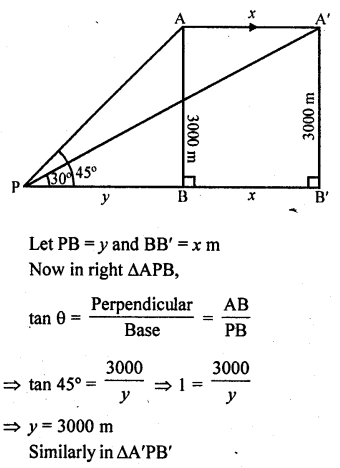

Question 64.
An aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°. Find the the speed of the aeroplane in km/hr.
Solution:
Let A be the aeroplane and AB is the height which 1 km and make an angle of elevations of 60° from a point P on the ground After moving 10 second’s flight, the angle of elevation becomes 30° from P
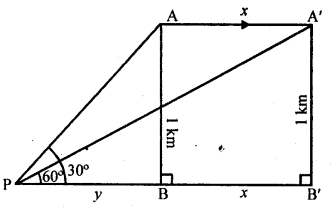
A’B’=AB =1 km = 1000 m
Let PB = y and BB’ = x
Now in right ΔAPB,

![]()
Question 65.
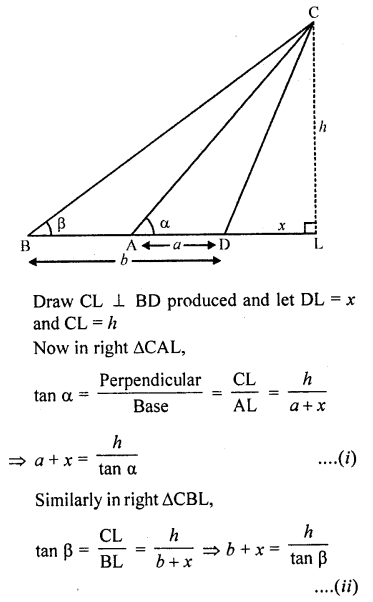
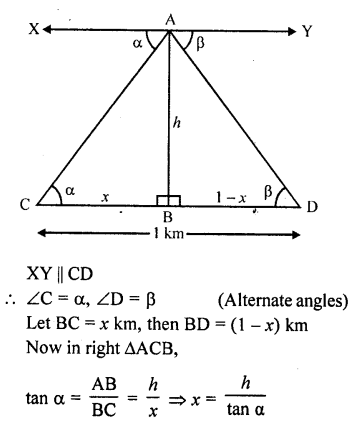
A tree standing on a horizontal plane is leaning towards east. At two points situated at distance a and b exactly due west on it, the angles of elevation of the top are respectively a and p. Prove that the height of the top from the ground is
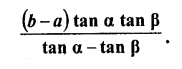
Solution:
Let CD is the tree which is leaning towardsEast and A and B are two points on the West making angles of elevation with top C of the tree as α and β
A and B are at the distance of a and b from the foot of the tree CD, then AD = a, BD = b
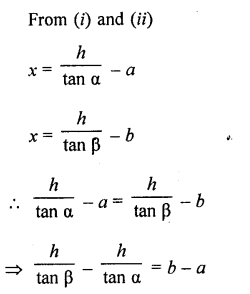
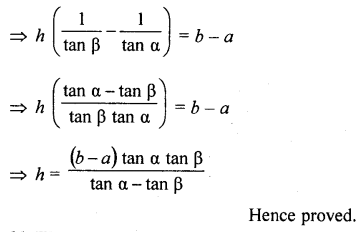
Question 66.
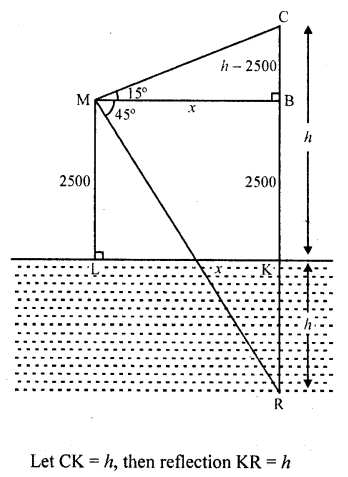
The angle of elevation of a stationery cloud from a point 2500 m above a lake is 15° and the angle of depression of its reflection in the lake is 45°. What is the height of the cloud above the lake level? (Use tan 15° = 0.268)
Solution:
Let C is the cloud over a lake LK
From a point M which, is 2500 m above the lake level, angle of elevation of C is 15° and angle of depression of the reflection of C in the lake which is R is 45°

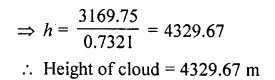
Question 67.
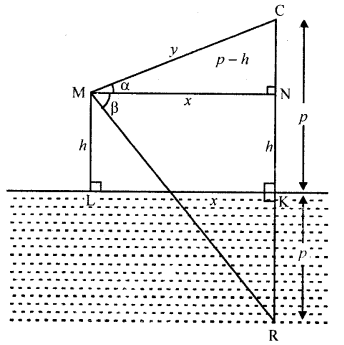
If the angle of elevation of a cloud from a point h metres above a lake is a and the angle of depression of its reflection in the lake be p, prove that the distance of the cloud from the point of \(\frac { 2h\sec { \alpha } }{ \tan { \beta -\tan { \alpha } } }\) [CBSE 2004]
Solution:
Let C be the cloud and from a point M which h m is above the lake level angle of elevation is α and angle of reflection of the cloud C, is β
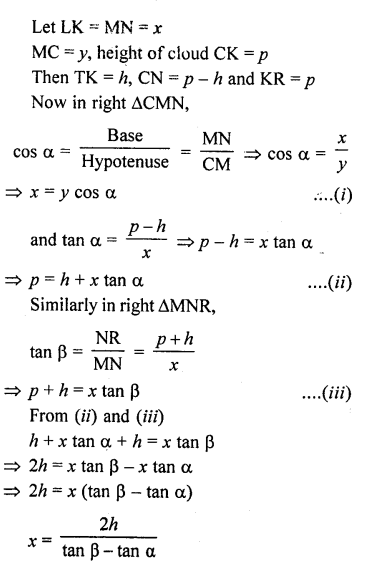

Question 68.
From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive mile stones on opposite sides of the aeroplane are observed to be a and p. Show that the height in miles of aeroplane above the road is given by \(\frac { \tan { \alpha } \tan { \beta } }{ \tan { \alpha } +\tan { \beta } }\) [CBSE 2004]
Solution:
Let A is aeroplane and C and D are two such points that the angles of depression from A are a and p respectively and CD = 1 km
Let height of the plane be h
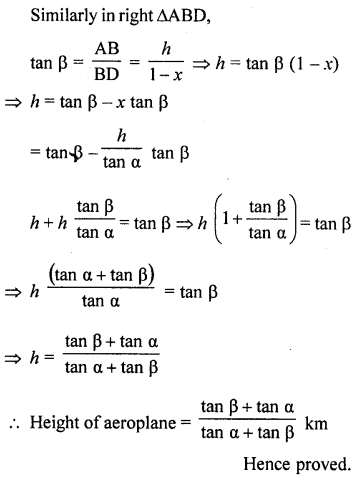
Question 69.
PQ is a post of given height a and AB is a tower at some distance. If a and p are the angles of elevation of B, the top of the tower, at P and Q respectively. Find the height of the tower and its distance from the post.
Solution:
Let PQ is post and AB is the tower Angles of elevation of B, from P and Q are a and P respectively
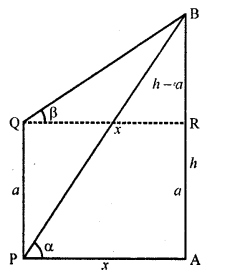

Question 70.
A ladder rests against a wail at an angle a to the horizontal. Its foot is pulled away from the wall through a distance a, so that it slides a distance b down the wall making an angle p with the horizontal.
Show that \(\frac { a }{ b }\) = \(\frac { \cos { \alpha } -\cos { \beta } }{ \sin { \beta } -\sin { \alpha } }\)
Solution:
In the figure, AC and ED is the same stair, so AC = ED
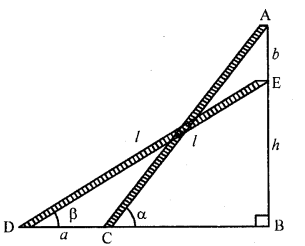

Question 71.
A tower subtends an angle a at a point A in the plane of its base and the angle of depression of the foot of the tower at a point b metres just above A is p. Prove that the height of the tower is b tan α cot β.
Solution:
Let TR is the tower which subtends angle α at a point A on the same plane
AB = b and angle of depression of R from B is β
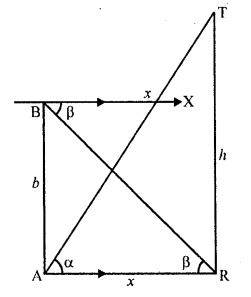

Question 72.
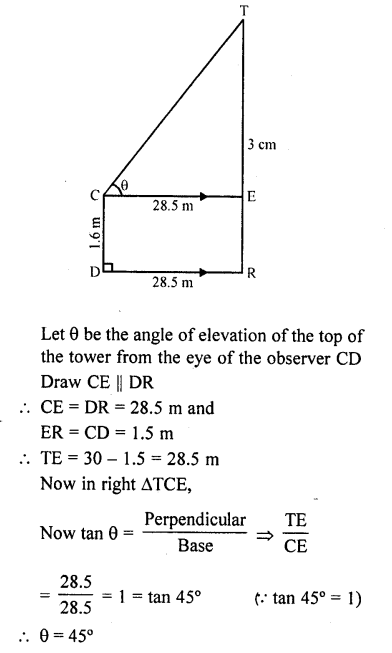
An observer, 1.5 m tall, is 28.5 m away from a tower 30 m high. Determine theangle of elevation of the top of the tower from his eye.
Solution:
Let TR is the tower and CD is the observer who is 28.5 m away from the tower TR
Height of the tower TR = 30 m
and height of observer CD = 1.5 m
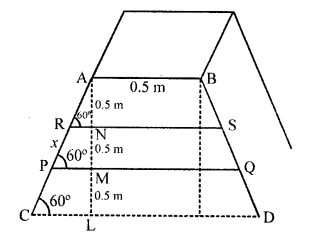
Question 73.
A carpenter makes stools for electricians with a square top of side 0.5 m and at a height of 1.5 m above the ground. Also, each leg is inclined at an angle of 60° to the ground. Find the length of each leg and also the lengths of two steps to be put at equal distances.
Solution:
Let AC be the leg of stool whose top in a square shaped of side AB = 0.5 m
Height of stool AL = 1.5 m, and angle of inclination by the leg of the stool = 60°


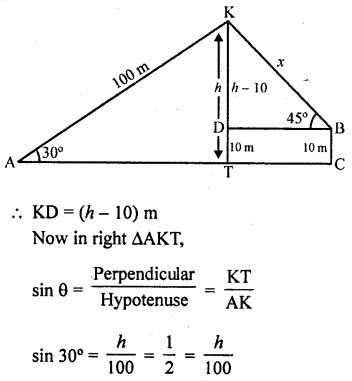
Question 74.
A boy is standing on the ground and flying a kite with 100 m of string at an elevation of 30°. Another boy is standing on the roof of a 10 m high building and is flying his kite at an elevation of 45°. Both the boys are on opposite sides of both the kites. Find the length of the string that the second boy must have so that the two kites meet.
Solution:
Let K be the kite. A and B are two boys flying kites. Boy B is standing on a building 10 m high
The string AK of kite of boy A is 100 m Let h be the height of the kite and x is the length of string of kite of second boy B

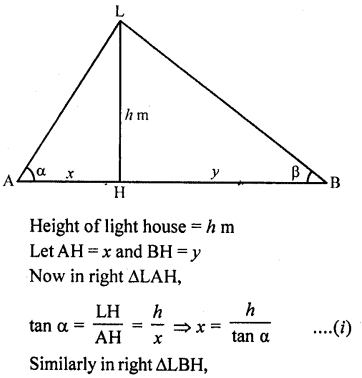
Question 75.
From the top of a light house, the angles of depression of two ships on the opposite sides of it are observed to be α and β. If the height of the light house be h metres and the line joining the ships passes through the foot of the light house, show that the distance between the ship is \(\frac { h(\tan { \alpha } +\tan { \beta } ) }{ \tan { \alpha } \tan { \beta } }\) meters.
Solution:
Let LH be the light house and A and B are two ships which make angles of elevation with L are a and p respectively

Question 76.
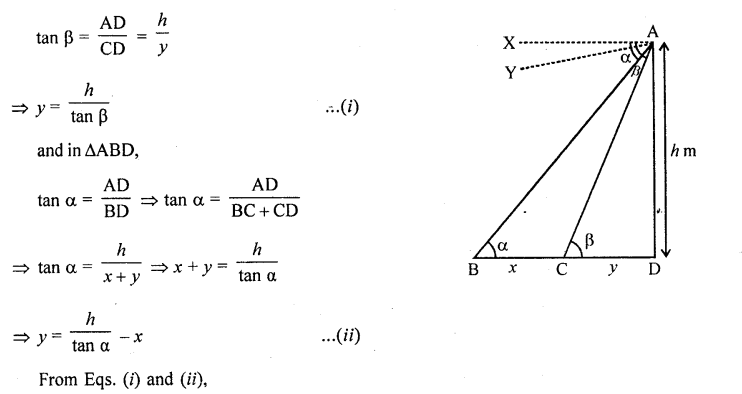
From the top of a tower hmetre high, the angles of depression of two objects, which are in the line with the foot of the tower are a and β (β > α). Find the distance between the two objects. [NCERT Exemplar]
Solution:
Let the distance between two objects is x m
and CD = y m
Given that, ∠BAX = α = ∠ABD [alternate angle]
∠CAY = β = ∠ACD [alternate angle]
and the height of tower, AD = h m Now, in ΔACD,

Question 77.
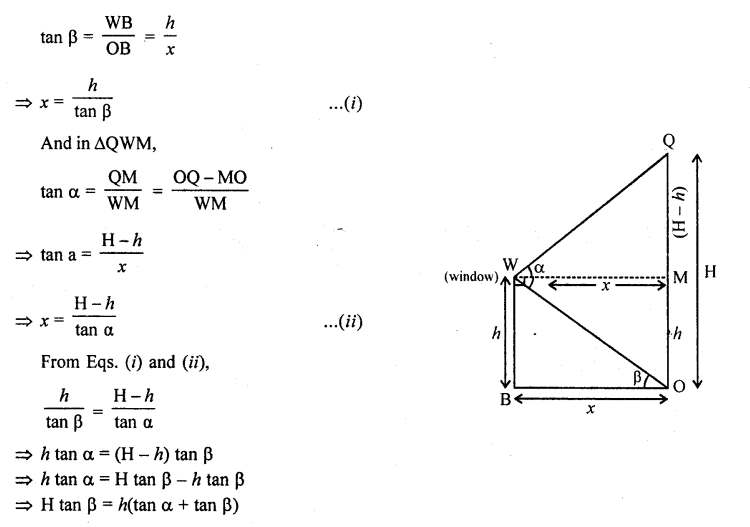
A window of a house is h metre above the ground. From the window, the angles of elevation and depression of the top and bottom of another house situated on the opposite side of the lane are found to be α and β respectively. Prove that the height of the house is h( 1 + tan α tan β) metres. [NCERT Exemplar]
Solution:
Let the height of the other house = OQ = H
and OB = MW = x m
Given that, height of the first house = WB = h = MO
and ∠QWM = α, ∠OWM =β= ∠WOB [alternate angle]
Now, in ΔWOB,
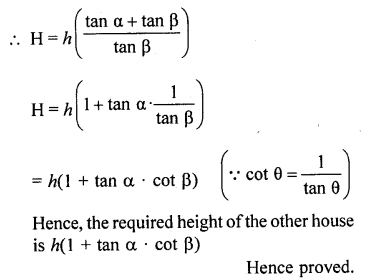
Question 78.
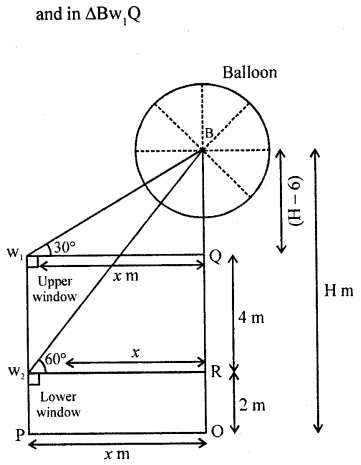
The lower window of a house is at a height of 2 m above the ground and its upper window is 4 m vertically above the lower window. At certain instant the angles of elevation of a balloon from these windows are observed to be 60° and 30° respectively. Find the height of the balloon above the ground.[NCERT Exemplar]
Solution:
Let the height of the balloon from above the ground is H.
A and OP = w2R = w1Q = x
Given that, height of lower window from above the ground = w2P = 2 m = OR
Height of upper window from above the lower window = w1w2 = 4 m = QR
∴ BQ = OB – (QR + RO)
BQ = H – (4 + 2)
BQ = H – 6
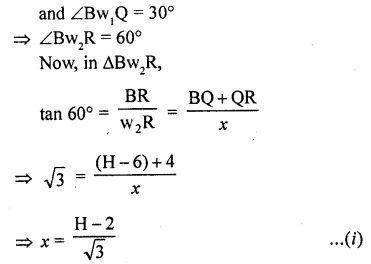
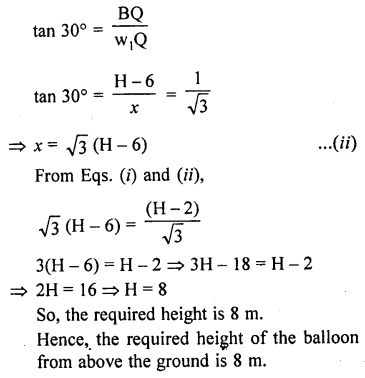
Hope given RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.