ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.2
These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.2
More Exercises
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.1
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.2
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.3
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles MCQS
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Chapter Test
Question 1.
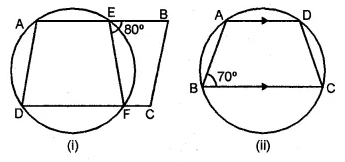
If O is the centre of the circle, find the value of x in each of the following figures (using the given information):
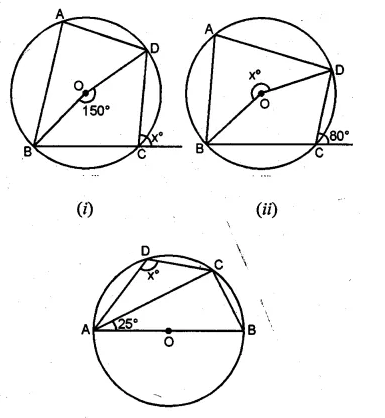
Solution:
From the figure
(i) ABCD is a cyclic quadrilateral
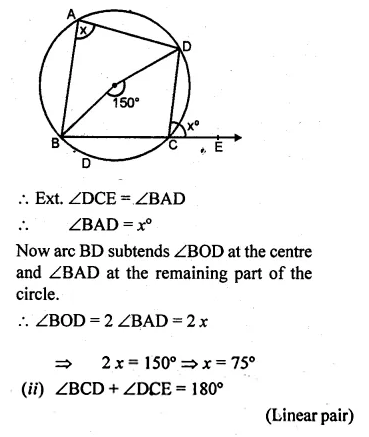
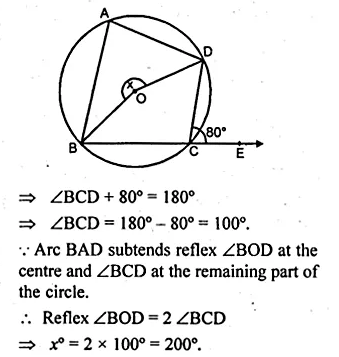
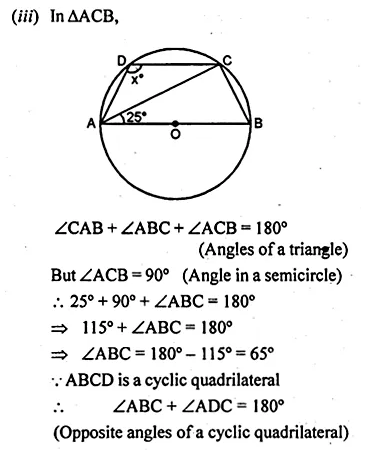
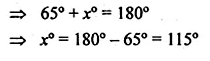
Question 2.
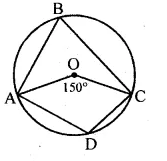
(a) In the figure (i) given below, O is the centre of the circle. If ∠AOC = 150°, find (i) ∠ABC (ii) ∠ADC.
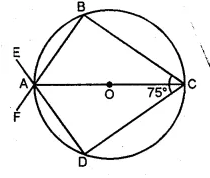
(b) In the figure (i) given below, AC is a diameter of the given circle and ∠BCD = 75°. Calculate the size of (i) ∠ABC (ii) ∠EAF.
Solution:
(a) Given, ∠AOC = 150° and AD = CD
We know that an angle subtends by an arc of a circle
at the centre is twice the angle subtended by the same arc
at any point on the remaining part of the circle.
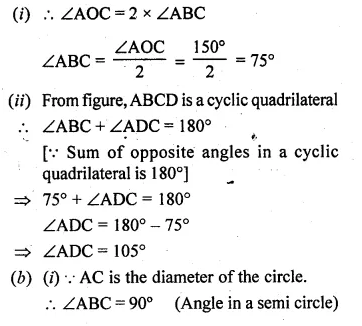

Question 3.
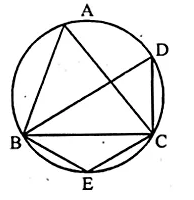
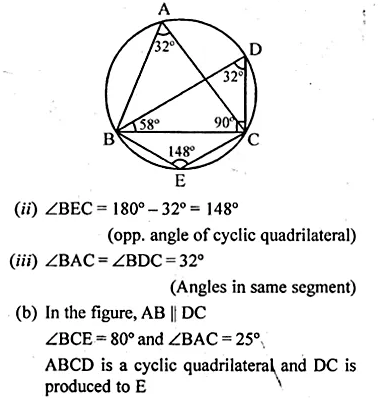
(a) In the figure, (i) given below, if ∠DBC = 58° and BD is a diameter of the circle, calculate:
(i) ∠BDC (ii) ∠BEC (iii) ∠BAC
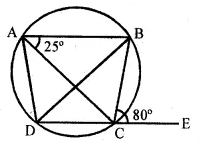
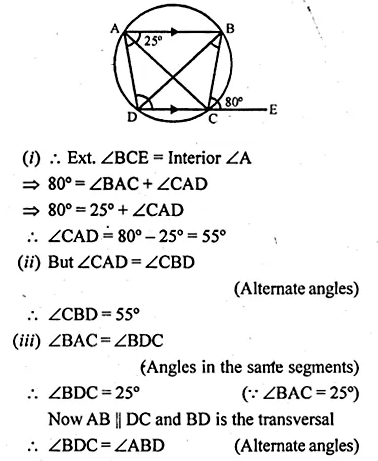
(b) In the figure (if) given below, AB is parallel to DC, ∠BCE = 80° and ∠BAC = 25°. Find:
(i) ∠CAD (ii) ∠CBD (iii) ∠ADC (2008)
Solution:
(a) ∠DBC = 58°
BD is diameter
∠DCB = 90° (Angle in semi circle)
(i) In ∆BDC
∠BDC + ∠DCB + ∠CBD = 180°
∠BDC = 180°- 90° – 58° = 32°

Question 4.
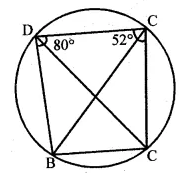
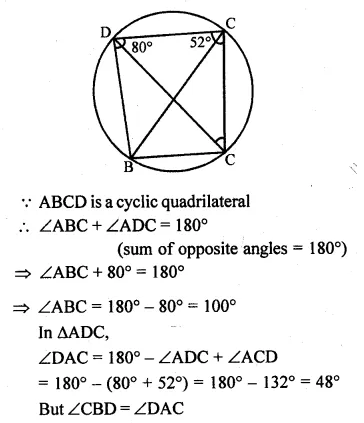
(a) In the figure given below, ABCD is a cyclic quadrilateral. If ∠ADC = 80° and ∠ACD = 52°, find the values of ∠ABC and ∠CBD.
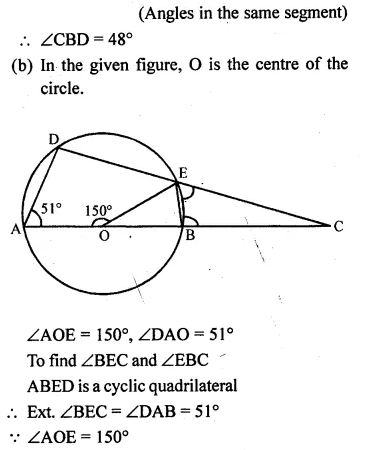
(b) In the figure given below, O is the centre of the circle. ∠AOE =150°, ∠DAO = 51°. Calculate the sizes of ∠BEC and ∠EBC.
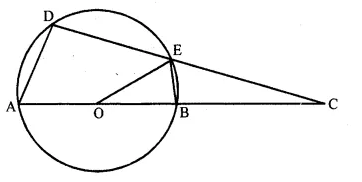
Solution:
(a) In the given figure, ABCD is a cyclic quadrilateral
∠ADC = 80° and ∠ACD = 52°
To find the measure of ∠ABC and ∠CBD

Question 5.
(a) In the figure (i) given below, ABCD is a parallelogram. A circle passes through A and D and cuts AB at E and DC at F. Given that ∠BEF = 80°, find ∠ABC.
(b) In the figure (ii) given below, ABCD is a cyclic trapezium in which AD is parallel to BC and ∠B = 70°, find:
(i)∠BAD (ii) DBCD.
Solution:
(a) ADFE is a cyclic quadrilateral
Ext. ∠FEB = ∠ADF
⇒ ∠ADF = 80°
ABCD is a parallelogram
∠B = ∠D = ∠ADF = 80°
or ∠ABC = 80°
(b)In trapezium ABCD, AD || BC
(i) ∠B + ∠A = 180°
⇒ 70° + ∠A = 180°
⇒ ∠A = 180° – 70° = 110°
∠BAD = 110°
(ii) ABCD is a cyclic quadrilateral
∠A + ∠C = 180°
⇒ 110° + ∠C = 180°
⇒ ∠C = 180° – 110° = 70°
∠BCD = 70°
Question 6.
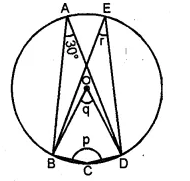
(a) In the figure given below, O is the centre of the circle. If ∠BAD = 30°, find the values of p, q and r.
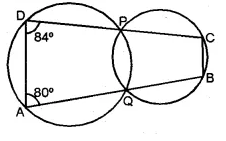
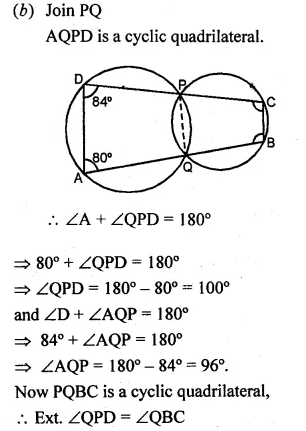
(b) In the figure given below, two circles intersect at points P and Q. If ∠A = 80° and ∠D = 84°, calculate
(i) ∠QBC (ii) ∠BCP
Solution:
(a) (i) ABCD is a cyclic quadrilateral
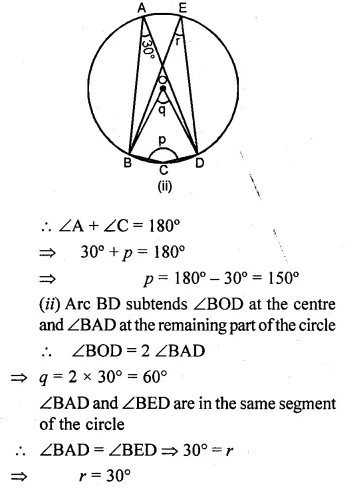
Question 7.
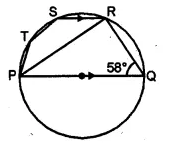
(a) In the figure given below, PQ is a diameter. Chord SR is parallel to PQ.Given ∠PQR = 58°, calculate (i) ∠RPQ (ii) ∠STP
(T is a point on the minor arc SP)
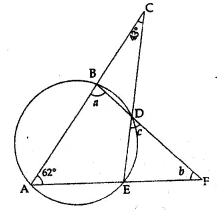
(b) In the figure given below, if ∠ACE = 43° and ∠CAF = 62°, find the values of a, b and c (2007)
Solution:
(a) In ∆PQR,
∠PRQ = 90° (Angle in a semi circle) and ∠PQR = 58°
∠RPQ = 90° – ∠PQR = 90° – 58° = 32°
SR || PQ (given)


Question 8.
(a) In the figure (i) given below, AB is a diameter of the circle. If ∠ADC = 120°, find ∠CAB.
(b) In the figure (ii) given below, sides AB and DC of a cyclic quadrilateral ABCD are produced to meet at E, the sides AD and BC are produced to meet at F. If x : y : z = 3 : 4 : 5, find the values of x, y and z.
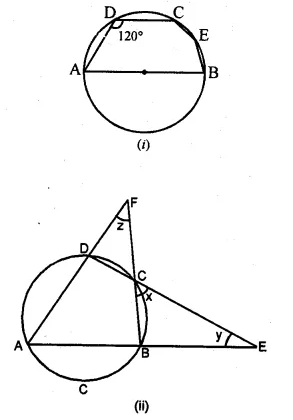
Solution:
(a) Construction: Join BC, and AC then
ABCD is a cyclic quadrilateral.
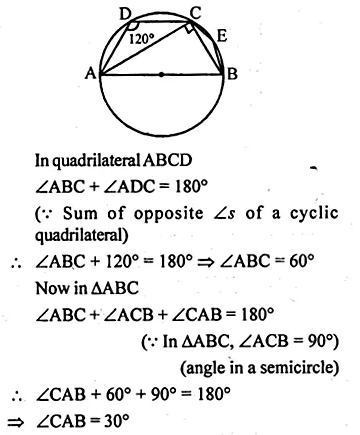
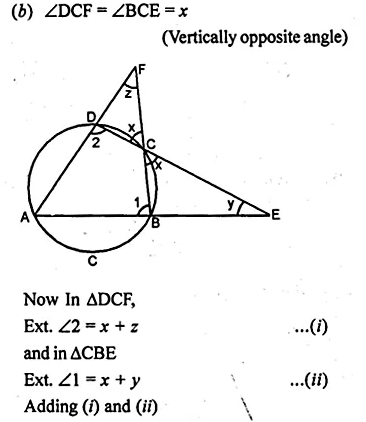
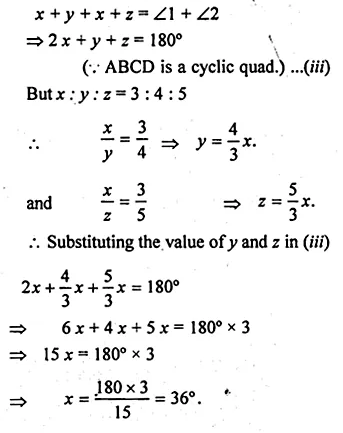
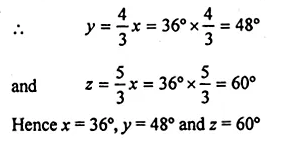
Question 9.
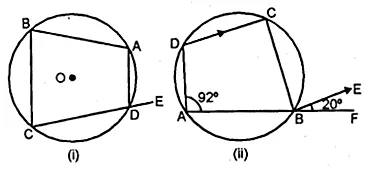
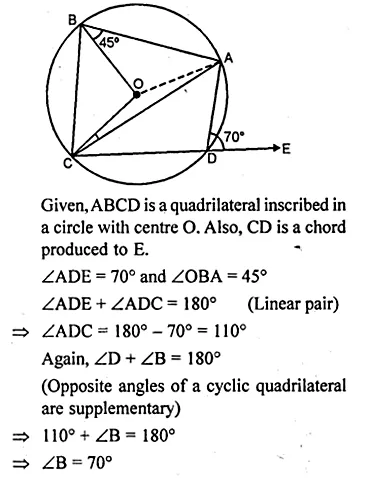
(a) In the figure (i) given below, ABCD is a quadrilateral inscribed in a circle with centre O. CD is produced to E. If ∠ADE = 70° and ∠OBA = 45°, calculate
(i) ∠OCA (ii) ∠BAC
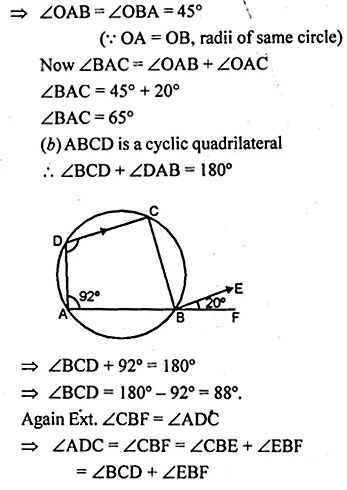
(b) In figure (ii) given below, ABF is a straight line and BE || DC. If ∠DAB = 92° and ∠EBF = 20°, find :
(i) ∠BCD (ii) ∠ADC.
Solution:
(a) ABCD is a cyclic quadrilateral


Question 10.
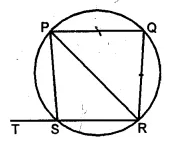
(a) In the figure (ii) given below, PQRS is a cyclic quadrilateral in which PQ = QR and RS is produced to T. If ∠QPR = 52°, calculate ∠PST.
(b) In the figure (ii) given below, O is the centre of the circle. If ∠OAD = 50°, find the values of x and y.
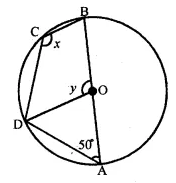
Solution:
(a) PQRS is a cyclic quadrilateral in which
PQ = QR
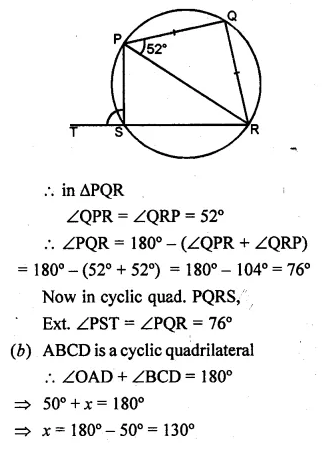
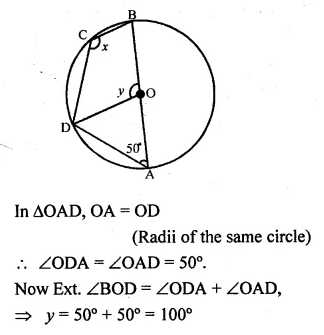
Question 11.
(a) In the figure (i) given below, O is the centre of the circle. If ∠COD = 40° and ∠CBE = 100°, then find :
(i) ∠ADC
(ii) ∠DAC
(iii) ∠ODA
(iv) ∠OCA.
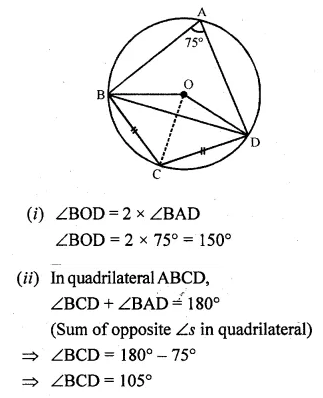
(b) In the figure (ii) given below, O is the centre of the circle. If ∠BAD = 75° and BC = CD, find :
(i) ∠BOD
(ii) ∠BCD
(iii) ∠BOC
(iv) ∠OBD (2009)
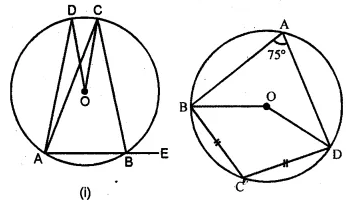
Solution:
(a) (i) ∴ ABCD is a cyclic quadrilateral.
∴ Ext. ∠CBE = ∠ADC
⇒ ∠ADC = 100°
(ii) Arc CD subtends ∠COD at the centre
and ∠CAD at the remaining part of the circle
∴ ∠COD = 2 ∠CAD
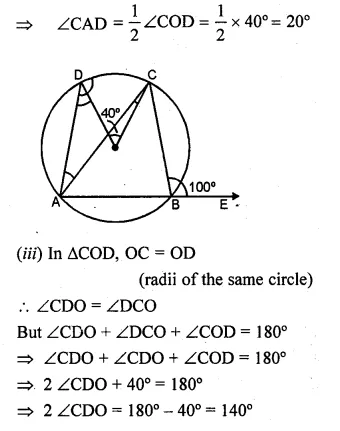

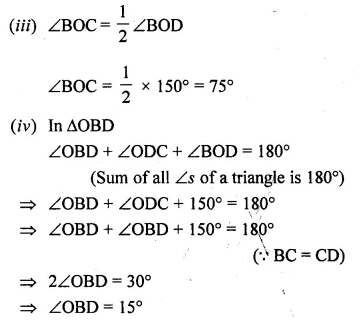
Question 12.
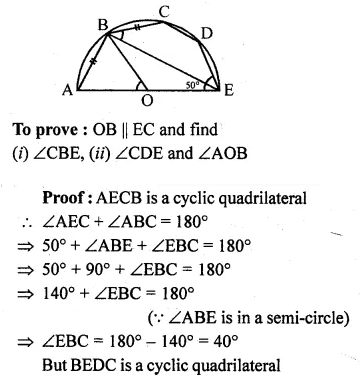
In the given figure, O is the centre and AOE is the diameter of the semicircle ABCDE. If AB = BC and ∠AEC = 50°, find :
(i) ∠CBE
(ii) ∠CDE
(iii) ∠AOB.
Prove that OB is parallel to EC.
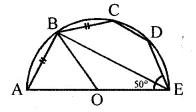
Solution:
In the given figure,
O is the centre of the semi-circle ABCDE
and AOE is the diameter. AB = BC, ∠AEC = 50°

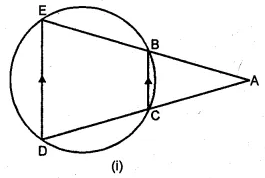
Question 13.
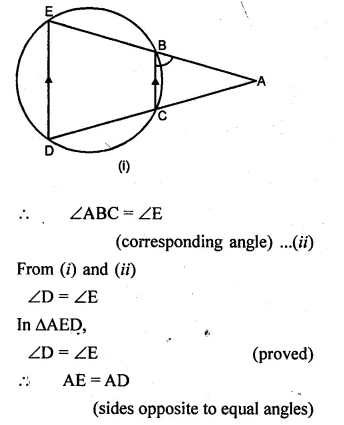
(a) In the figure (i) given below, ED and BC are two parallel chords of the circle and ABE, ACD are two st. lines. Prove that AED is an isosceles triangle.
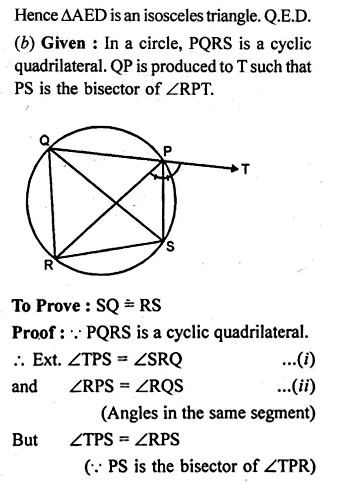
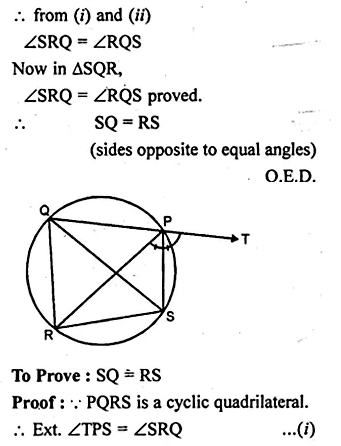
(b) In the figure (ii) given below, SP is the bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that SQ = RS.
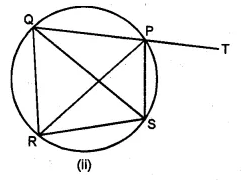
Solution:
(a) Given: Chord BC || ED,
ABE and ACD are straight lines.
To Prove: ∆AED is an isosceles triangle.
Proof: BCDE is a cyclic quadrilateral.
Ext. ∠ABC = ∠D …(i)
But BC || ED (given)

Question 14.
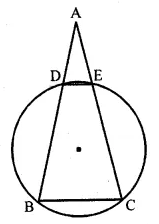
In the given figure, ABC is an isosceles triangle in which AB = AC and circle passing through B and C intersects sides AB and AC at points D and E. Prove that DE || BC.
Solution:
In the given figure,
∆ABC is an isosceles triangle in which AB = AC.
A circle passing through B and C intersects
sides AB and AC at D and E.
To prove: DE || BC
Construction : Join DE.
∵ AB = AC
∠B = ∠C (angles opposite to equal sides)
But BCED is a cyclic quadrilateral
Ext. ∠ADE = ∠C
= ∠B (∵ ∠C = ∠B)
But these are corresponding angles
DE || BC
Hence proved.
Question 15.
(a) Prove that a cyclic parallelogram is a rectangle.
(b) Prove that a cyclic rhombus is a square.
Solution:
(a) ABCD is a cyclic parallelogram.
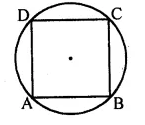
To prove: ABCD is a rectangle
Proof: ABCD is a parallelogram
∠A = ∠C and ∠B = ∠D

Question 16.
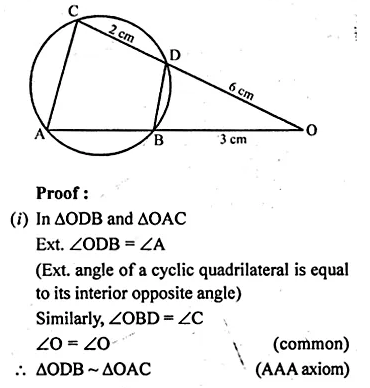
In the given figure, chords AB and CD of the circle are produced to meet at O. Prove that triangles ODB and OAC are similar. Given that CD = 2 cm, DO = 6 cm and BO = 3 cm, area of quad. CABD
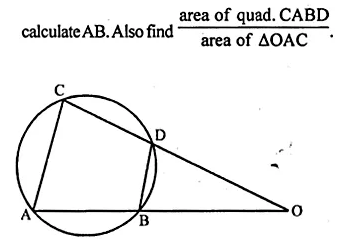
Solution:
In the given figure, AB and CD are chords of a circle.
They are produced to meet at O.
To prove : (i) ∆ODB ~ ∆OAC
If CD = 2 cm, DO = 6 cm, and BO = 3 cm
To find : AB and also area of the
\(\frac { Quad.ABCD }{ area\quad of\quad \Delta OAC } \)
Construction : Join AC and BD


Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.2 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.