ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Chapter Test
These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Chapter Test
More Exercises
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.1
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.2
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.3
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles MCQS
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Chapter Test
Question 1.
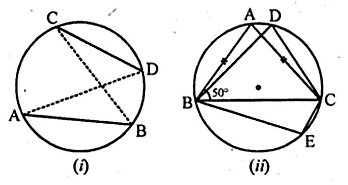
(a) In the figure (i) given below, triangle ABC is equilateral. Find ∠BDC and ∠BEC.
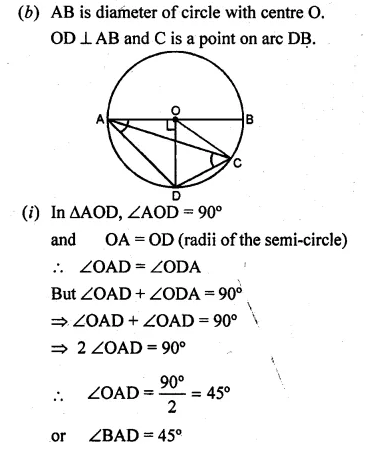
(b) In the figure (ii) given below, AB is a diameter of a circle with centre O. OD is perpendicular to AB and C is a point on the arc DB. Find ∠BAD and ∠ACD
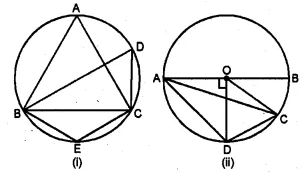
Solution:
(a) ∆ABC is an equilateral triangle.
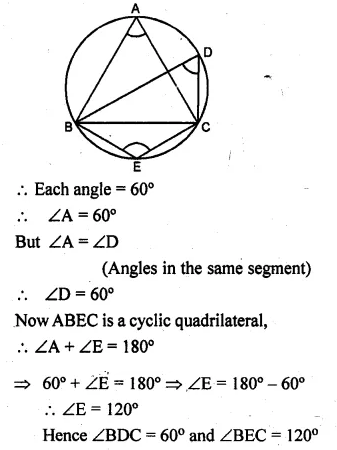

Question 2.
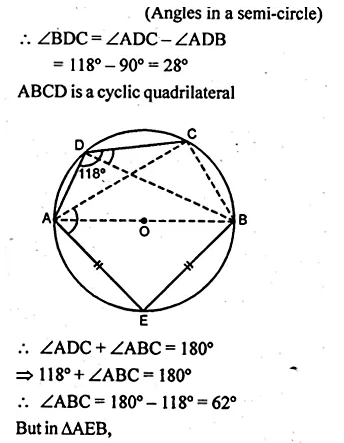
(a) In the figure given below, AB is a diameter of the circle. If AE = BE and ∠ADC = 118°, find
(i) ∠BDC (ii) ∠CAE.
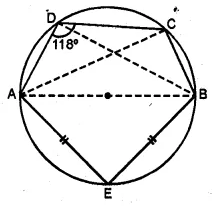
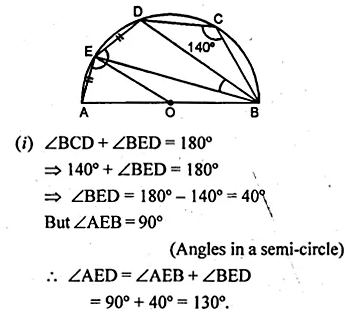
(b) In the figure given below, AB is the diameter of the semi-circle ABCDE with centre O. If AE = ED and ∠BCD = 140°, find ∠AED and ∠EBD. Also Prove that OE is parallel to BD.

Solution:
(a) Join DB, CA and CB.
∠ADC = 118° (given)
and ∠ADB = 90°


Question 3.
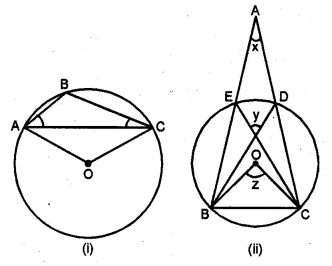
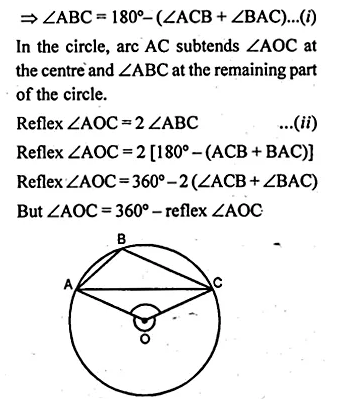
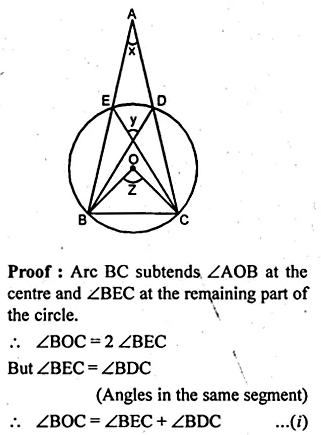
(a) In the figure (i) given below, O is the centre of the circle. Prove that ∠AOC = 2 (∠ACB + ∠BAC).
(b) In the figure (ii) given below, O is the centre of the circle. Prove that x + y = z.
Solution:
(a) Given: O is the centre of the circle.
To Prove : ∠AOC = 2 (∠ACB + ∠BAC).
Proof: In ∆ABC,
∠ACB + ∠BAC + ∠ABC = 180° (Angles of a triangle)

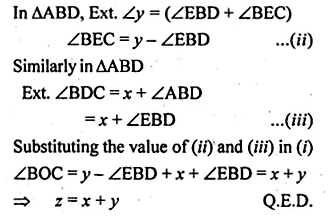
Question 4.
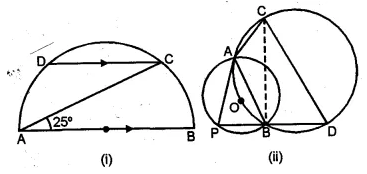
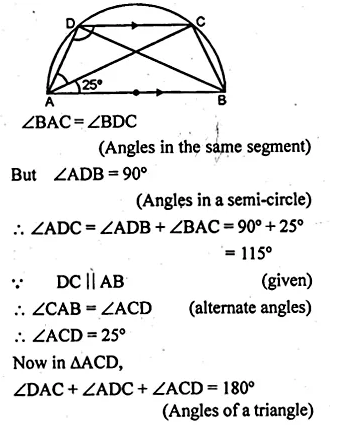
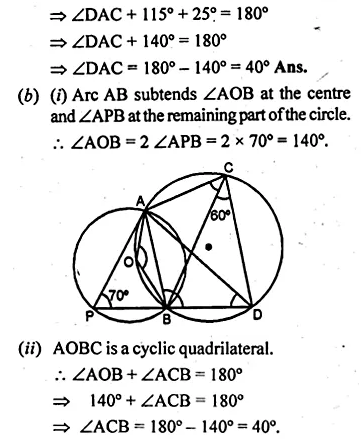
(a) In the figure (i) given below, AB is the diameter of a circle. If DC is parallel to AB and ∠CAB = 25°, find :
(i)∠ADC (ii) ∠DAC.
(b) In the figure (ii) given below, the centre O of the smaller circle lies on the circumference of the bigger circle. If ∠APB = 70° and ∠BCD = 60°, find :
(i) ∠AOB (ii) ∠ACB
(iii) ∠ABD (iv) ∠ADB.
Solution:
(a) AB is diameter and DC || AB,
∠CAB = 25°, join AD,BD

Question 5.
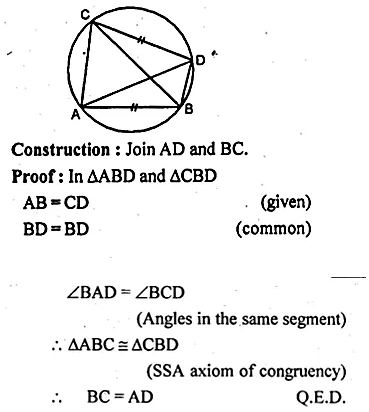
(a) In the figure (i) given below, ABCD is a cyclic quadrilateral. If AB = CD, Prove that AD = BC.
(b) In the figure (ii) given below, ABC is an isosceles triangle with AB = AC. If ∠ABC = 50°, find ∠BDC and ∠BEC.
Solution:
(a) Given : ABDC is a cyclic quadrilateral AB = CD.
To Prove: AD = BC.

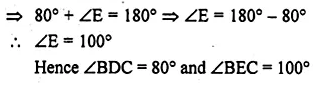
Question 6.
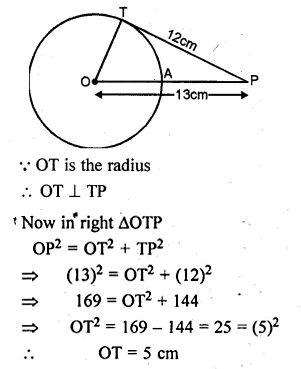
A point P is 13 cm from the centre of a circle. The length of the tangent drawn from P to the circle is 12 cm. Find the distance of P from the nearest point of the circle.
Solution:
Join OT, OP = 13 cm and TP = 12 cm
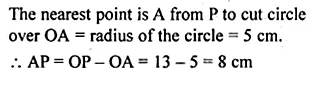
Question 7.
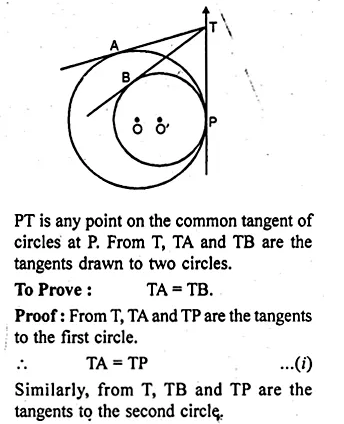
Two circles touch each other internally. Prove that the tangents drawn to the two circles from any point on the common tangent are equal in length.
Solution:
Given: Two circles with centre O and O’
touch each other internally at P.

Question 8.
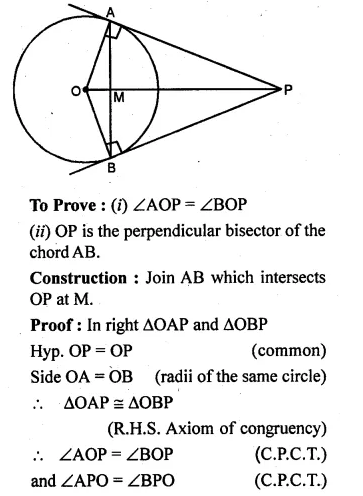
From a point outside a circle, with centre O, tangents PA and PB are drawn. Prove that
(i) ∠AOP = ∠BOP.
(ii) OP is the perpendicular bisector of the chord AB.
Solution:
Given: From a point P, outside the circle with centre O.
PA and PB are the tangents to the circle,
OA, OB and OP are joined.

Question 9.
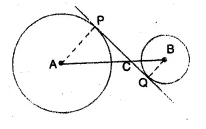
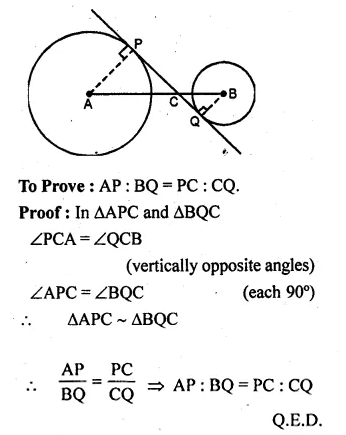
(a) The figure given below shows two circles with centres A, B and a transverse common tangent to these circles meet the straight line AB in C. Prove that:
AP : BQ = PC : CQ.
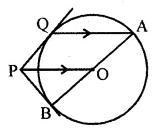
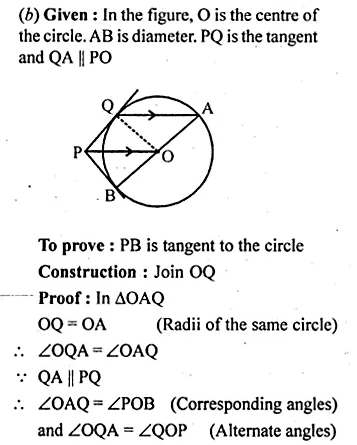
(b) In the figure (ii) given below, PQ is a tangent to the circle with centre O and AB is a diameter of the circle. If QA is parallel to PO, prove that PB is tangent to the circle.
Solution:
(a) Given: Two circles with centres A and B
and a transverse common tangent to these circles meets AB at C.

Question 10.
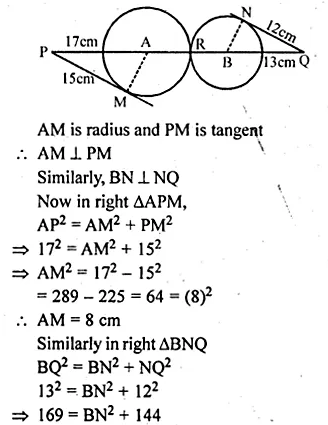
In the figure given below, two circles with centres A and B touch externally. PM is a tangent to the circle with centre A and QN is a tangent to the circle with centre B. If PM = 15 cm, QN = 12 cm, PA = 17 cm and QB = 13 cm, then find the distance between the centres A and B of the circles.
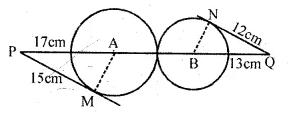
Solution:
In the given figure, two chords with centre A and B touch externally.
PM is a tangent to the circle with centre A
and QN is tangent to the circle with centre B.
PM = 15 cm, QN = 12 cm, PA = 17 cm, QB = 13 cm.
We have to find AB.

Question 11.
Two chords AB, CD of a circle intersect externally at a point P. If PB = 7 cm, AB = 9 cm and PD = 6 cm, find CD.
Solution:
∵ AB and CD are two chords of a circle
which intersect each other at P, outside the circle.
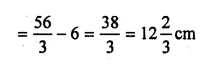
Question 12.
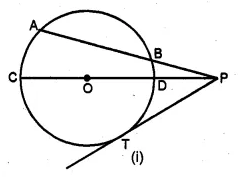
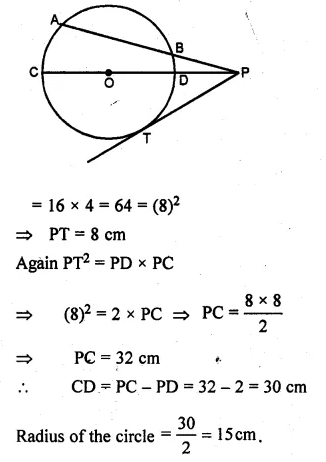
(a) In the figure (i) given below, chord AB and diameter CD of a circle with centre O meet at P. PT is tangent to the circle at T. If AP = 16 cm, AB = 12 cm and DP = 2 cm, find the length of PT and the radius of the circle
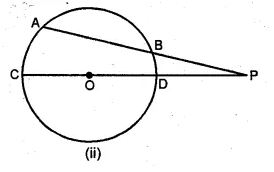
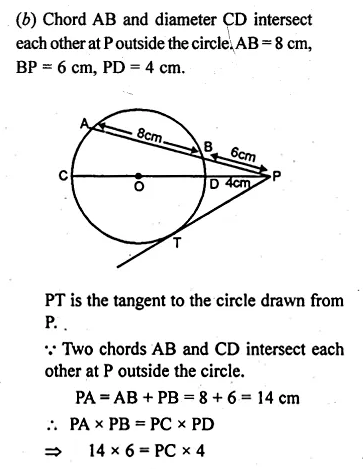
(b) In the figure (ii) given below, chord AB and diameter CD of a circle meet at P. If AB = 8 cm, BP = 6 cm and PD = 4 cm, find the radius of the circle. Also, find the length of the tangent drawn from P to the circle. .
Solution:
Given : (a) AB is a chord of a circle with centre O
and PT is tangent and CD is the diameter of the circle
which meet at P.
AP = 16 cm, AB = 12 cm, OP = 2 cm
∴PB = PA – AB = 16 – 12 = 4 cm
∵ABP is a secant and PT is tangent.
∴PT² = PA × PB.

Question 13.
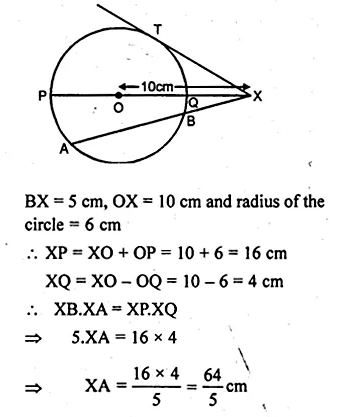
In the figure given below, chord AB and diameter PQ of a circle with centre O meet at X. If BX = 5 cm, OX = 10 cm and.the radius of the circle is 6 cm, compute the length of AB. Also, find the length of tangent drawn from X to the circle.
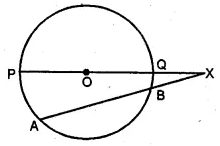
Solution:
Chord AB and diameter PQ meet at X
on producing outside the circle
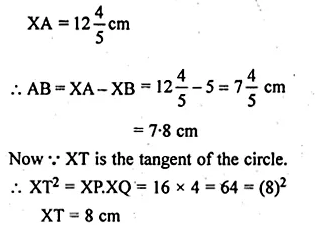
Question 14.
(a) In the figure (i) given below, ∠CBP = 40°, ∠CPB = q° and ∠DAB = p°. Obtain an equation connecting p and q. If AC and BD meet at Q so that ∠AQD = 2 q° and the points C, P, B and Q are concyclic, find the values of p and q.
(b) In the figure (ii) given below, AC is a diameter of the circle with centre O. If CD || BE, ∠AOB = 130° and ∠ACE = 20°, find:
(i)∠BEC (ii) ∠ACB
(iii) ∠BCD (iv) ∠CED.
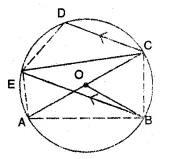
Solution:
(a) (i) Given : ABCD is a cyclic quadrilateral.
Ext. ∠PBC = ∠ADC
⇒ 40° = ∠ADC
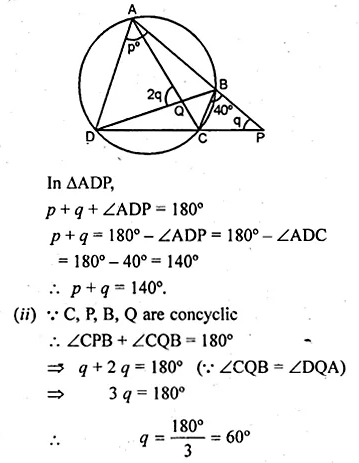
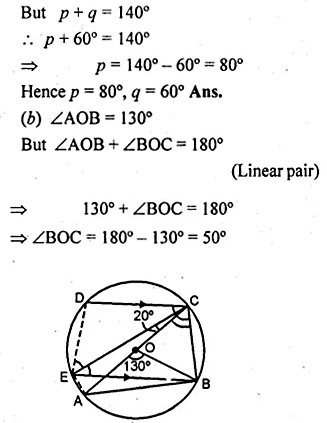

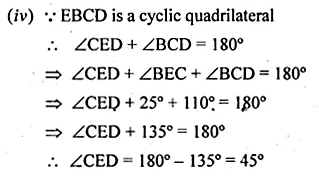
Question 15.
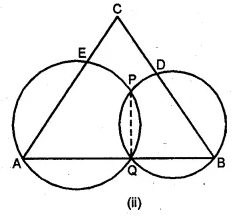
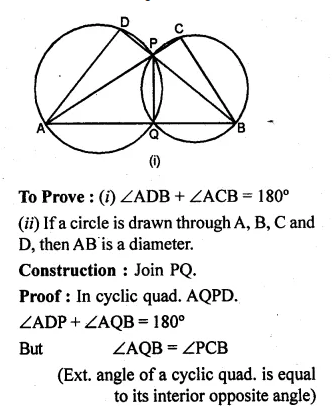
(a) In the figure (i) given below, APC, AQB and BPD are straight lines.
(i) Prove that ∠ADB + ∠ACB = 180°.
(ii) If a circle can be drawn through A, B, C and D, Prove that it has AB as a diameter
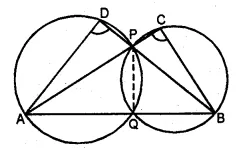
(b) In the figure (ii) given below, AQB is a straight line. Sides AC and BC of ∆ABC cut the circles at E and D respectively. Prove that the points C, E, P and D are concyclic.
Solution:
(a) Given: In the figure, APC,
AQB and BPD are straight lines.

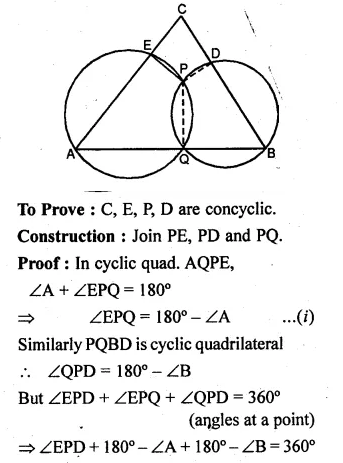

Question 16.
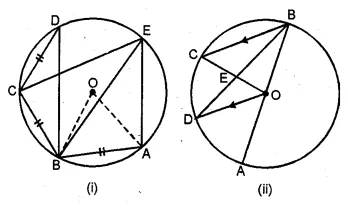
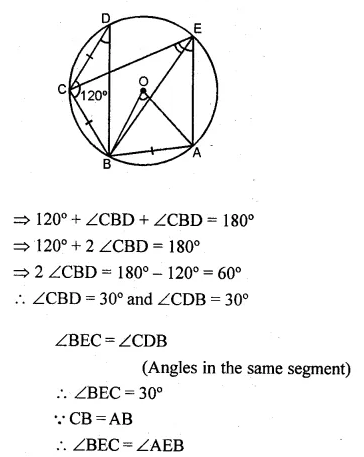
(a) In the figure (i) given below, chords AB, BC and CD of a circle with centre O are equal. If ∠BCD = 120°, find
(i) ∠BDC (ii) ∠BEC
(iii) ∠AEC (iv) ∠AOB.
Hence Prove that AOAB is equilateral.
(b) In the figure (ii) given below, AB is a diameter of a circle with centre O. The chord BC of the circle is parallel to the radius OD and the lines OC and BD meet at E. Prove that
(i) ∠CED = 3 ∠CBD (ii) CD = DA.
Solution:
(a) In ∆BCD, BC = CD
∠CBD = ∠CDB
But ∠BCD + ∠CBD + ∠CDB = 180°
(∵ Angles of a triangle)



Question 17.
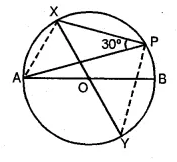
(a) In the adjoining figure, (i) given below AB and XY are diameters of a circle with centre O. If ∠APX = 30°, find
(i) ∠AOX (ii) ∠APY (iii) ∠BPY (iv) ∠OAX.
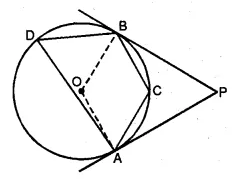
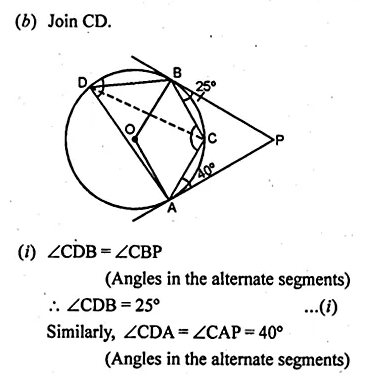
(b) In the figure (ii) given below, AP and BP are tangents to the circle with centre O. If ∠CBP = 25° and ∠CAP = 40°, find :
(i) ∠ADB (ii) ∠AOB (iii) ∠ACB (iv) ∠APB.
Solution:
(a) AB and XY are diameters of a circle with centre O.
∠APX = 30°.
To find :
(i) ∠AOX (ii) ∠APY
(iii) ∠BPY (iv) ∠OAX
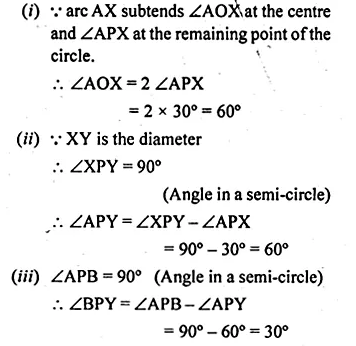
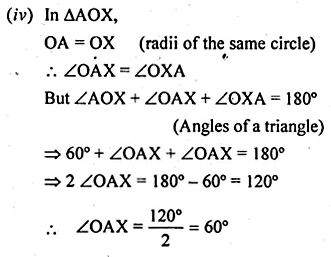

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Chapter Test are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.