CBSE Sample Papers for Class 12 Maths Paper 5 are part of CBSE Sample Papers for Class 12 Maths. Here we have given CBSE Sample Papers for Class 12 Maths Paper 5.
CBSE Sample Papers for Class 12 Maths Paper 5
| Board | CBSE |
| Class | XII |
| Subject | Maths |
| Sample Paper Set | Paper 5 |
| Category | CBSE Sample Papers |
Students who are going to appear for CBSE Class 12 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme as prescribed by the CBSE is given here. Paper 5 of Solved CBSE Sample Paper for Class 12 Maths is given below with free PDF download solutions.
Time: 3 Hours
Maximum Marks: 100
General Instructions:
- All questions are compulsory.
- Questions 1-4 in section A are very short answer type questions carrying 1 mark each.
- Questions 5-12 in section B are short answer type questions carrying 2 marks each.
- Questions 13-23 in section C are long answer I type questions carrying 4 marks each.
- Questions 24-29 in section D are long answer II type questions carrying 6 marks each.
SECTION A
Question 1.
What is the principal value of \({ tan }^{ -1 }\left( tan\frac { 2\pi }{ 3 } \right)\)
Question 2.
If A is a square matrix of order 3 x 3 and |3A| = k |A|, then find the value of k.
Question 3.
What is the distance of the point (p, q, r) from the x-axis?
Question 4.
Let f: R → R be defined by f(x) = 3x2 – 5 and g : R → R be defined by g(x) = \(\frac { x }{ { x }^{ 2 }+1 }\). Find fog.
SECTION B
Question 5.
Show that the relation R in the set A = {1, 2, 3, 4, 5} given by R = {(a, b): |a – b| is even} is an equivalence relation.
Question 6.
Let li, mi, ni For i = 1, 2, 3 be the direction cosines of three mutually perpendicular vectors in space. Show that AA’ = I3.
Where
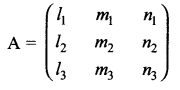
Question 7.
Form the differential equation corresponding to the function y2 = a(b – x) (b + x) by eliminating a and b.
Question 8.
If ey (x + 1) = 1, prove that \(\frac { dy }{ dx }\) = -ey
Question 9.
Find the Cartesian and vector equations of line which passes through the point (-2, 4, -5) and parallel to the line given by
\(\frac { x+3 }{ 3 } =\frac { 4-y }{ -5 } =\frac { 8-z }{ -6 }\)
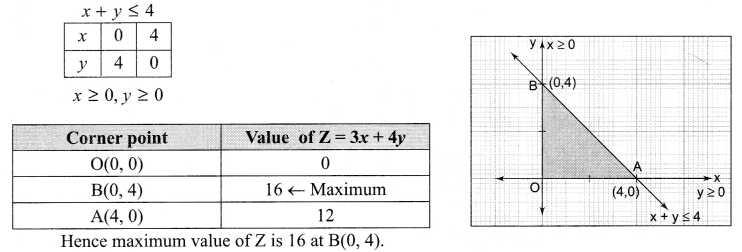
Question 10.
Solve the following L.R.R graphically
Maximise Z = 3x + 4y
Subject to constraints x + y ≤ 4, x ≥ 0, y ≥ 0
Question 11.
If P (E) = 0.35, P(F) = 0.45, P(E ∪ F) = 0.65. Find (i) P (E|F) (ii) P(E ∩ \(\bar { F }\)).
Question 12.
Find the points on the curve y = x3 at which the slope of the tangent is equal to y-coordinate of the point.
SECTION C
Question 13.
Find the area of the region bounded by the y-axis, y = cos x and y = sin x, 0 ≤ x ≤ \(\frac { \pi }{ 4 }\).
Question 14.
Evaluate \(\int _{ 0 }^{ 4 }{ \left( 2{ x }^{ 2 }+5x \right) } dx\) dx as a limit of sum.
Question 15.
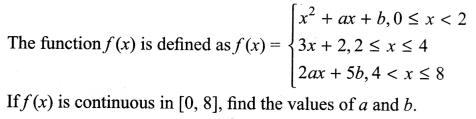
Question 16.

Question 17.
Use differentials to find the approximate value of \(\frac { 1 }{ { \left( 2.002 \right) }^{ 2 } }\)
OR
Find the intervals for which the function f(x) = sin x – cos x is increasing or decreasing in [0, 2π].
Question 18.
Solve the differential equation y dx + (x – y2) dy = 0
OR
Solve the differential equation \(\frac { dy }{ dx } =\frac { x+y+1 }{ x+y }\)
Question 19.
A bag contains (2n + 1) coins. It is known that n of these coins have a head on both its sides whereas the rest of the coins are fair. A coin is picked up at random from the bag and is tossed. If the probability that the toss results in a head is \(\frac { 31 }{ 42 }\). Find the value of n.
Question 20.
A plane meets the coordinate axis in A, B and C such that the centroid of ΔABC is the point (α, β, γ). Show that the equation of the plane is \(\frac { x }{ \alpha } +\frac { y }{ \beta } +\frac { z }{ \gamma } =3\).
Question 21.
Two cards are drawn simultaneously without replacement from a well shuffled pack of 52 cards. Find the mean and variance of number of red cards.
Question 22.
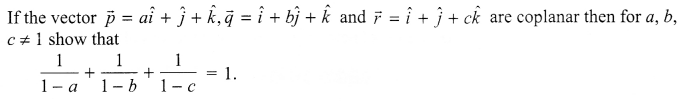
Question 23.
If a 20 year old girl drives her car at 25 km/h, she has to spend ₹ 4/km on petrol. If she drives her car at 40 km/h, the petrol cost increases to ₹ 5/km. She has ₹ 200 to spend on petrol and wishes to find the maximum distance she can travel within one hour. Express the above problem as L.P.P. Write any one value reflected in the problem.
SECTION D
Question 24.
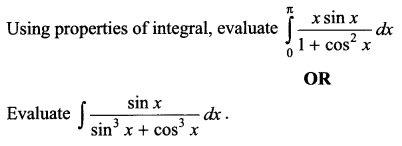
Question 25.
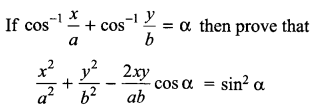
OR
Let N be the set of all natural numbers and let R be a relation in N x N defined by (a, b) R (c, d) ⇒ ad = bc
For all (a, b), (c, d) ∈ N x N, show that R is an equivalence relation on N x N.
Question 26.
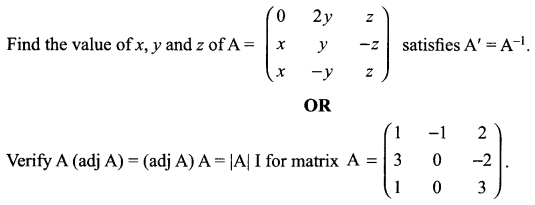
Question 27.
Define skew lines. Using only vector approach, find the shortest distance between the following two skew lines
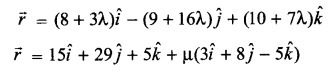
Question 28.
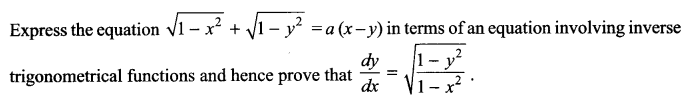
Question 29.
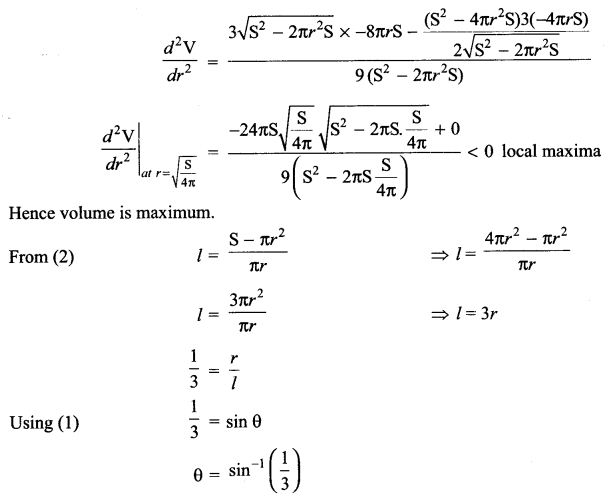
Show that the semivertical angle of a right circular cone of given surface area and maximum volume is \({ sin }^{ -1 }\left( \frac { 1 }{ 3 } \right)\)
Solutions
Solution 1.
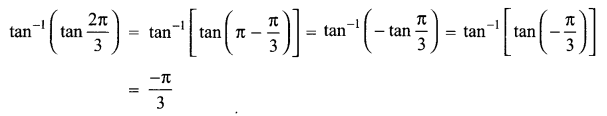
Solution 2.
A is a square matrix of order 3 x 3
|3A| = k|A| ⇒ |3A| = 33 |A| = 27 |A| = k |A|
So k = 27.
Solution 3.
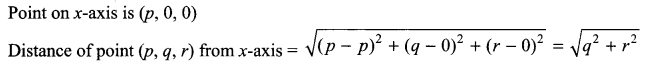
Solution 4.
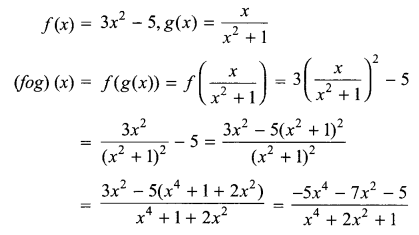
Solution 5.
A= {1,2, 3, 4, 5}
R = {(a, b): |a- b| is even}
Reflexive: (a, a): |a – a| = 0 is even
So (a, a) ∈ R, ∀ a ∈A
So R is reflexive.
Symmetric: (a, b): |a – b| is even, ∀ (a, b) ∈ R
= |b – a| is even
= (b, a) ∈ R
So R is symmetric.
Transitive: Let (a, b), (b, c) ∈ R
(a, b): |a – b| is even and (b, c): |b – c| is even.
a – b = ± 2m, b – c = ± 2n, ∀ m, n ∈ N
a – c = ± 2m ± 2n = ± 2 (m + n)
|a – c| is even.
So (a, c) ∈ R.
So R is transitive.
Since R is reflexive, symmetric and transitive, so R is an equivalence relation.
Solution 6.
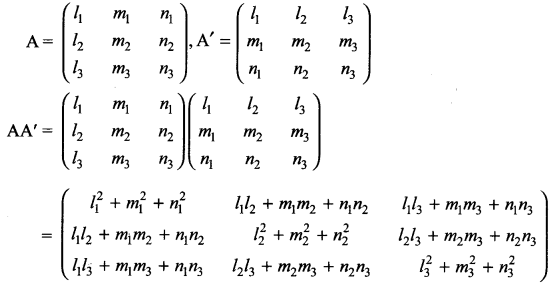
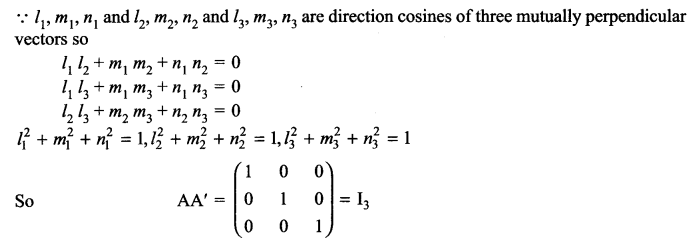
Solution 7.

Solution 8.
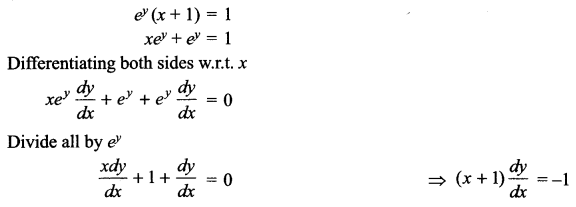
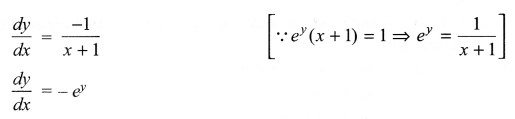
Solution 9.
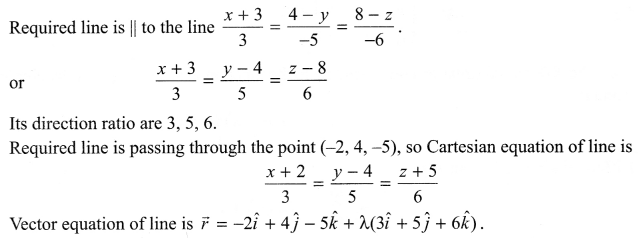
Solution 10.
Solution 11.
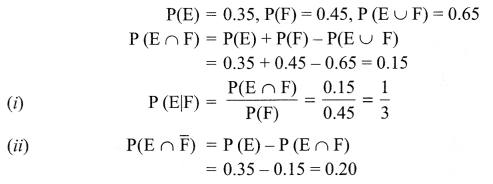
Solution 12.
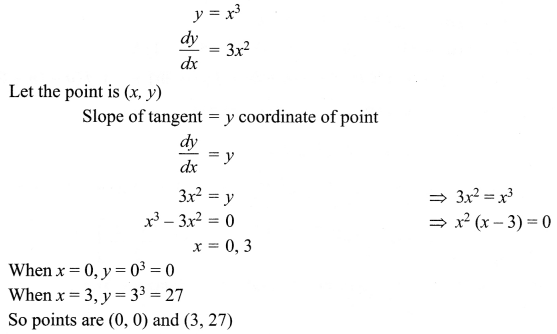
Solution 13.
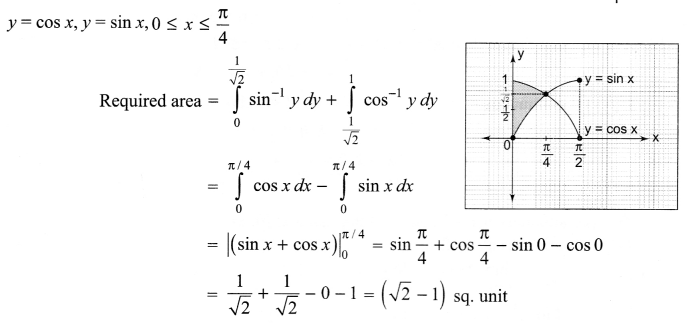
Solution 14.
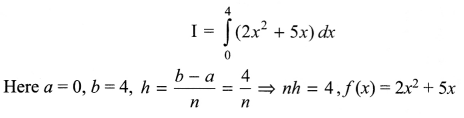

Solution 15.

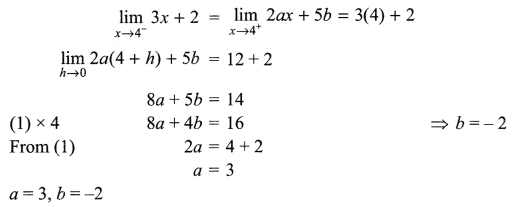
Solution 16.

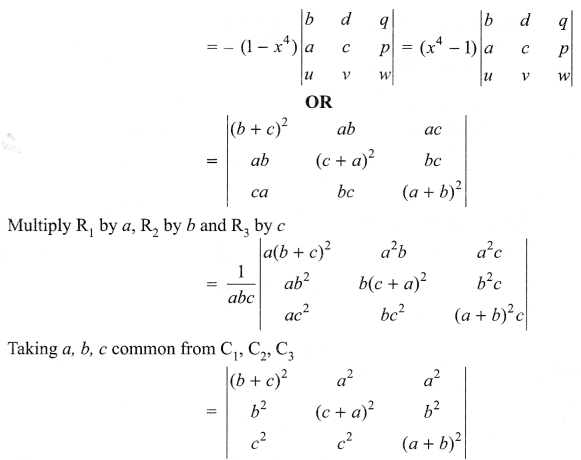


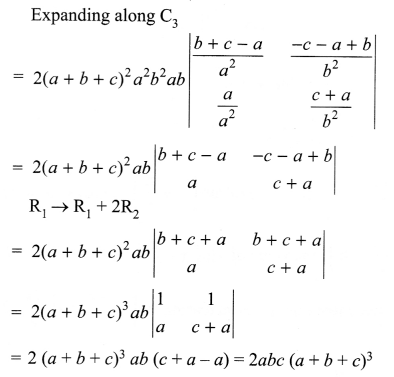
Solution 17.

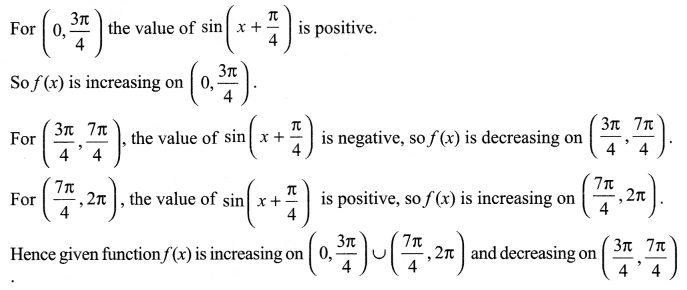
Solution 18.
![]()


Solution 19.
Let E1 is the event: Coin having head on both sides
E2 is the event: Coin is fair.
A is the event: head comes upon tossing a coin
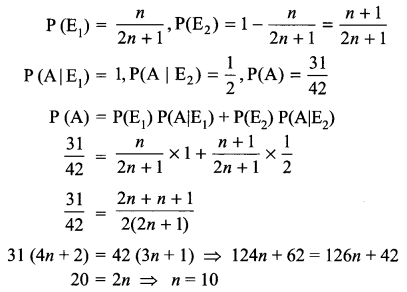
Solution 20.

Solution 21.
Let Random variable x denote the number of red cards drawn.
Possible values of x are 0, 1, 2
Two cards are drawn simultaneously without replacement.
Total cards = 52, Red cards = 26
Remaining cards = 26

Solution 22.
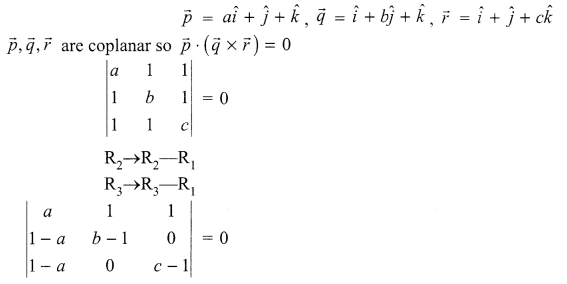
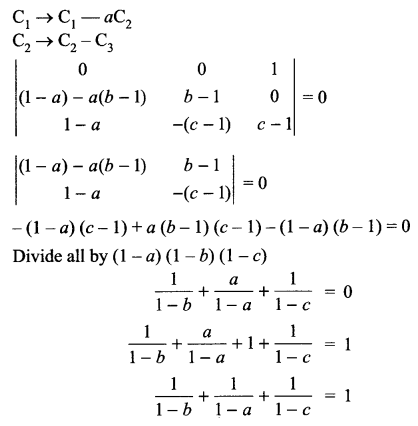
Solution 23.
Let distance covered with speed of 25 km/h is x km, distance covered with speed of 40 km/h is y km.
Objective function is maximize distance = Z = x + y,
Subject to constraints are
4x + 5y ≤ 200
x ≥ 0, y ≥ 0
Value: At slow speed consumption of petrol is low, so maintain normal speed and save petrol.
Solution 24.
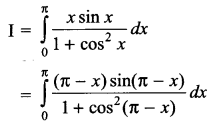
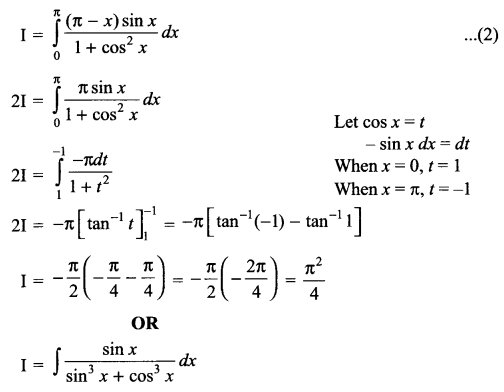

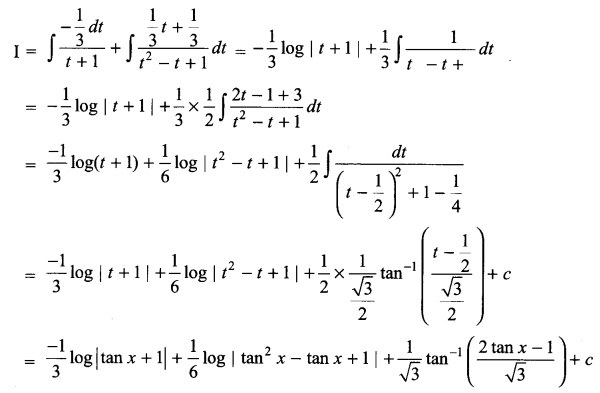
Solution 25.

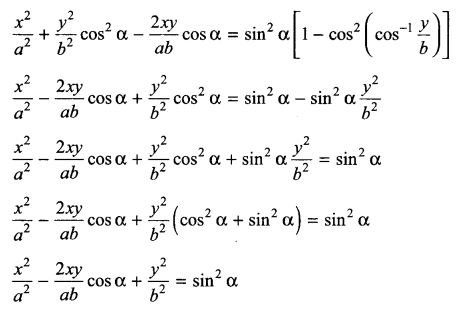
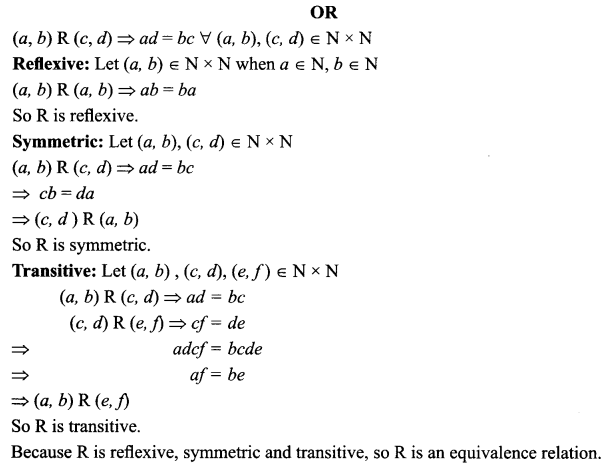
Solution 26.
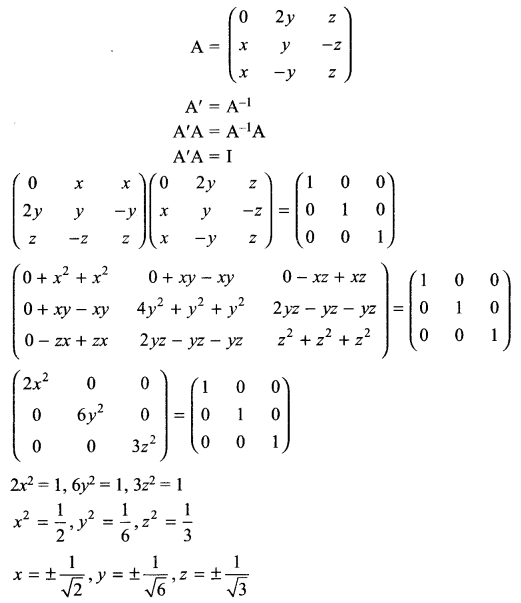
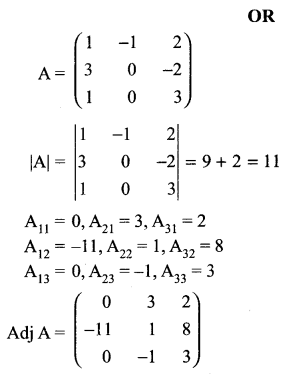
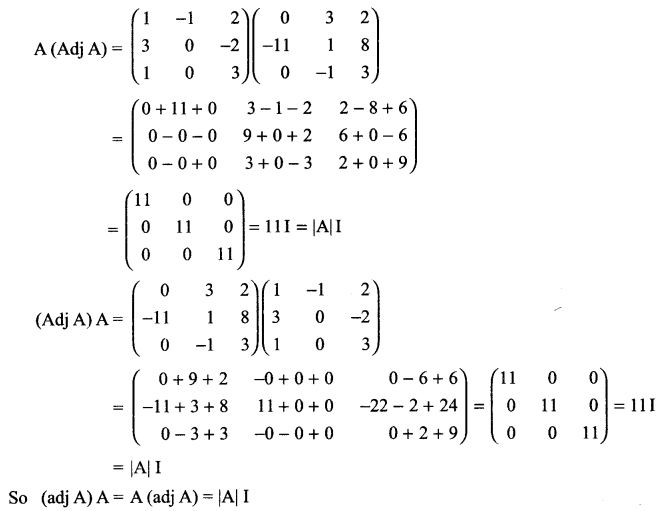
Solution 27.
Skew lines: The lines which are neither intersecting nor parallel are called skew lines.
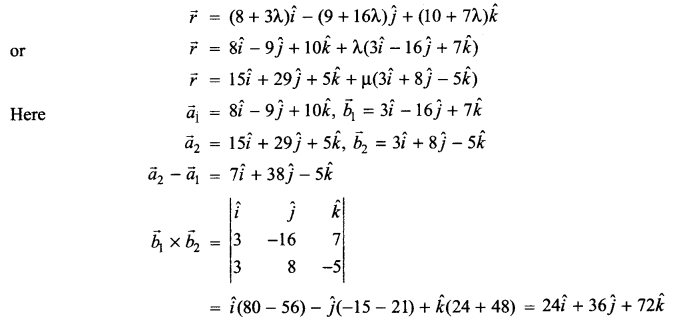

Solution 28.

Solution 29.
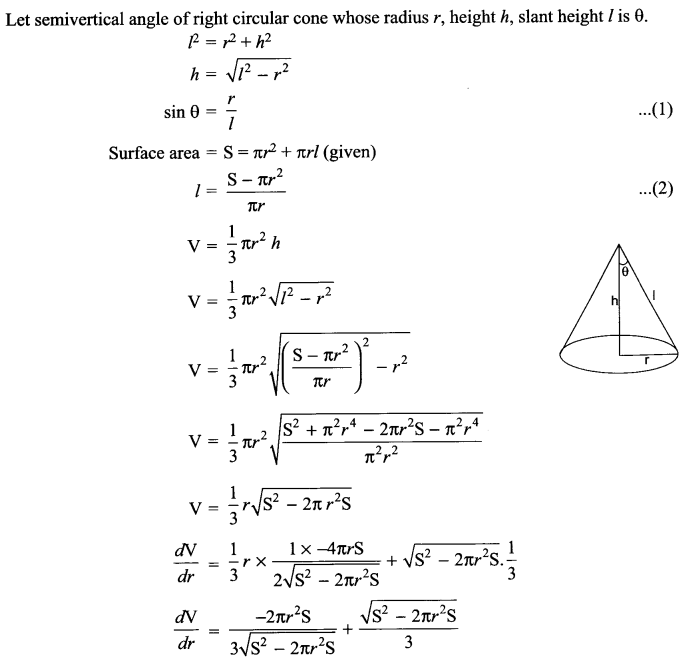
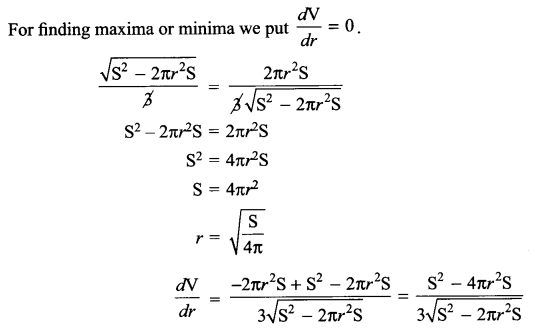
We hope the CBSE Sample Papers for Class 12 Maths Paper 5 help you. If you have any query regarding CBSE Sample Papers for Class 12 Maths Paper 5, drop a comment below and we will get back to you at the earliest.