CBSE Sample Papers for Class 10 Maths Standard Term 2 Set 2 with Solutions

Students can access the CBSE Sample Papers for Class 10 Maths with Solution and marking scheme Term 2 Set 2 will help students in understanding the difficulty level of the exam.

CBSE Sample Papers for Class 10 Maths Standard Term 2 Set 2 with Solutions

Time : 2 Hr.
Max. Marks : 40

General Instructions :

• The question paper consists of 14 questions divided into three Sections A, B, C.
• All questions are compulsory.
• Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
• Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
• Section C comprises of 4 questions of 4 marks each. An internal choice has been provided in one question. It contains two case study based questions.

Section – A

Question 1.
The solution of a quadratic equation is as follows : (2)
\(x =\frac{8 \pm \sqrt{(-8)^{2}-4(3)(2)}}{2(3)}\)
Then find the quadratic equation.
Answer:
Given, x = \(\frac{8 \pm \sqrt{(-8)^{2}-4(3)(2)}}{2(3)}\)
Thus, a = 3,b = -8 and c = 2
The equation is given by
ax² + bx + c = 0
Hence, 3x² – 8x + 2 = 0.

Question 2.
Is the roots of the equation x² – 3x – 9 = 0 are real and distinct? (2)
OR
Find the nature of roots of the quadratic equation 2x² – 4x + 3 = 0.
Answer:
Given, x² – 3x – 9 =0
Now, D = b² – 4ac
= (-3)² – 4(1)(-9)
= 9 + 36
= 45 > 0
Thus, the roots are real and distinct.
OR
Given, 2x² – 4x + 3 = 0
Comparing it with quadratic equation
ax² + bx + c =0
Here,a = 2, b = -4 and c = 3.
D = b² – 4ac
= (-4)² – 4 x (2) (3)
= 16 – 24
= – 8 < 0
Hence, D < 0 this shows that roots will be imaginary.

Question 3.
From an external point P, tangents PA and PB are drawn to a circle with centre O. If CD is the tangent to the circle at a point E and PA = 14 cm, find the perimeter of ∆PCD. (2)

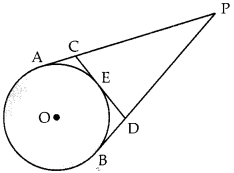
Answer:
We have, AP PB, [Tangents from point P]
AC = CE, (Tangents from point C]
BD = DE [Tangents from point D]
Thus, CD = CE + ED – AC + BD
Now, CP = AP – AC – 14 – AC
and PD = BP – BD = 14 – BD [AP BP; from above]
Now, Perimeter of ∆PCD = CP + CD + DP
= 14 – AC + AC + BD + 14 – BD
= 28 cm.

Question 4.
Two cubes each of side 4 cm are joined end to end to form a solid. Find the surface area of the resulting cuboid. (2)
Answer:
Given, side of each cube (a) =4 cm
Thus, length of the larger solid = (4 + 4) cm = 8 cm
Width of the larger solid = 4 cm
Height of the larger solid = 4 cm
Thus, surface area of the resultant cuboid = 2(4 × 8 + 4 × 4 +4 × 8) cm²
= 2(32 + 16 + 32) cm²
= (2 × 80) cm²
= 160 cm^2.

Question 5.
If the mean of frequency distribution is 8.1 and \(\Sigma f_{i} x_{i}=132+5 k, \Sigma f_{i}=20\), then k = ? (2)
Answer:
Given:
\(\Sigma f_{i} x_{i}=132+5 k\)
\(\Sigma f_{i}=20\)
Mean = 8.1
Then,
Mean = \(\frac{\Sigma f_{i} x_{i}}{\Sigma f_{i}}=\frac{132+5 k}{20}\)
⇒ \(8.1=\frac{132+5 k}{20}\)
⇒ 162 = 132 + 5k
⇒ 5k = 30
⇒ k = 6

Question 6.
What is the common difference of an A.P. in which a₂₁ – a₇ = 84? (2)
Answer:
Given, a₂₁ – a₇ = 84
∴ (a + 20d) – (a + 6d) = 84 [ ∵  a_n = a + (n – 1) d]
⇒ 20d – 6d = 84
⇒ 14d = 84
⇒ d = 6.

Section – B

Question 7.
Draw a line segment of length 8 cm and divide it internally in the ratio 4:5. (3)
Answer:
Step I: Draw AB = 8 cm
Step II: Draw any ray AX making an acute angle with AB.

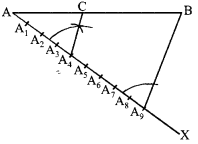
Step III: Draw 9(4 + 5) points on ray AX namely A₁, A₂, A₃, A₄, A₅, A_6, A₇, A₈, A₉ at equal distance.
Step IV: Join BA₉
Step V: Through point A₄, draw a line parallel to A₉B intersecting AB at the point C then AC : CB = 4 : 5.
BD = AB – AD = 6 – 2.54 = 3.46 m

Question 8.
In the given figure, AB is 6 m high pole and CD is a ladder inclined at an angle of 60° to the horizontal and reaches upto a point D of pole. If AD = 2.54 m. Find the length of the ladder. (Use √ 3 = 1.73) (3)

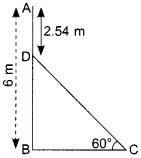
OR
If a tower 30 m high, casts a shadow 10V3 m long on the ground, then what is the angle of elevation of the sun?
Answer:
\(\sin 60^{\circ}=\frac{\mathrm{BD}}{\mathrm{DC}}\)
\(\frac{\sqrt{3}}{2}=\frac{3.46}{D C}\)
\(\mathrm{DC}=\frac{3.46 \times 2}{\sqrt{3}}=4 \mathrm{~m}\)
∴ Length of the ladder, DC =4 m (∵ √ 3 = 1.732)
OR

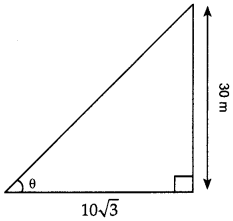
Let required angle be θ.
\(\tan \theta=\frac{30}{10 \sqrt{3}}\)
\(\tan \theta=\sqrt{3}\)
tan θ = tan 60°
∴ θ = 60°.

Question 9.
The following table shows the age distribution of cases of a certain disease admitted during a year in a particular hospital:

class	5-14	15-24	25-34	35-44	45-54	55-64
Frequency	6	11	21	23	14	5

Find the average age for which maximum cases occurred.(3)
Answer:

Age (in years) (in years) ;	4.5 – 14.5	14.5 – 24.5	24.5 – 34.5	34.5 – 44.5	44.5 – 54.5	54.5 – 64.5
No. of   cases	6	11	21	23	14	5

Here, highest frequency group = 34.5 – 44.5
Modal class = 34.5 – 44.5
Thus,l = 34.5, h = 10, f₁= 23, f₀ = 21, f₂ = 14
Mode = \(l+\left(\frac{f_{1}-f_{0}}{2 f_{1}-f_{0}-f_{2}}\right) \times h\)
= \(34.5+\left(\frac{23-21}{46-21-14}\right) \times 10\)
= \(34.5+\frac{2}{11} \times 10\)
= 34.5 + 1.81
= 36.31.

Question 10.
Calculate the mean of the following data : (3)

Class Interval	0-10	10-20	20-30	30-40	40-50
Frequency	12	16	6	7	9

Answer:

Class Interval	Frequency (fi)	Class Marks (xi)	(fi × xi)
0-10	12	5	60
10-20	16	15	240
20-30	6	25	150
30-40	7	35	245
40 – 50	9	45	405
	5£ = 50		\(\Sigma\left(f_{i} \times x_{i}\right)\) = 1100

We know that
Mean = \(\frac{\Sigma\left(f_{i} \times x_{i}\right)}{\Sigma f_{i}}\)
= \(\frac{1100}{50}\)
= 22.

Section – C

Question 11.
A takes 6 days less than B to do a work. If both A and B working together can do it in 4 days, how many days will B take to finish it? (4)
OR
Two water taps together take 6 hours to fill a tank. If the tap with the larger diameter takes 9 hours lesser than the tap with the smaller diameter, then find the time in which each tap can separately fill the tap.
Answer:
Let B can finish a work in x days
So, A can finish work in (x – 6) days.
Together they finish the work in 4 days
According to the question,
\(\frac{1}{x}+\frac{1}{x-6}=\frac{1}{4}\)
⇒ \(\frac{x-6+x}{(x)(x-6)}=\frac{1}{4}\)
⇒ = 4(2x – 6)=x² – 6x
⇒ 8x — 24 = x² – 6x
⇒ x² – 14x + 24 = 0
⇒ x² – 12x – 2x + 24 = 0
⇒ x (x -12) – 2(x – 12) = 0
⇒ (x – 12) (x – 2) = 0
Either x – 12 = 0 or x – 2 = 0
x = 12 or x = 2, Rejected
Hence, B can finish work in 12 days.
A can finish work in 6 days.
OR
Let the smaller tap fill the tank in x hr and the total capacity of the tank be 1 unit.
Then in 1 hr. it can fill \(\frac{1}{x}\) unit.
So the larger tank takes (x – 9) hours to fill the tank.
Then in 1 hr, it can fill \(\frac{1}{x – 9}\) unit.
Together they can fill the tank in 6 hours.
Then in 1 hour, they can fill \(\frac{1}{6}\) unit of the tank.
Thus,
⇒ \(\frac{1}{x}+\frac{1}{x – 9}=\frac{1}{6}\)
⇒ \(\frac{x – 9 + x}{x(x – 9)}=\frac{1}{6}\)
⇒ \(\frac{2 x – 9}{x(x – 9)}=\frac{1}{6}\)
⇒ x² – 9x – 12x + 54 = 0
⇒ x² – 21x + 54 = 0
⇒ x² – 18x – 3x + 54 = 0
⇒ x(x – 18) – 3(x – 18) = 0
⇒ (x – 18)(x – 3) = 0
⇒ x = 3, 18.

As 9 hours less than 3 hours is -6 which is not possible, so the smaller tap takes 18 hours to fill the tank and the larger takes 9 hours to do so.

Question 12.
In Fig., XY and X’Y’ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X’Y’ at B. Prove that ∠AOB = 90°. (4)

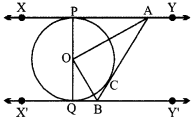
Answer:
Join OC. In ∆XAPO and ∆ACO, we have
AP = AC [Tangents drawn from external point A]
AO = OA [Common]
PO = OC [Radii of the same circle]

∆APO ≅ ∆ACO [By SSS criterion of congruence]
∴ ∠PAO = ∠CAO [By C.P.C.T.]
∴ ∠PAC =2 ∠CAO
Similarly, we can prove that
∆OQB ≅ ∆OCB
∠QBO = ∠CBO
⇒ ∠CBQ = 2 ∠CBO
Now, ∠TAC + ∠CBQ = 180° [Sum of interior angles on the same side of transversal is 180°]
⇒ 2 ∠CAO + 2 ∠CBO = 180°
⇒ ∠CAO + ∠CBO = 90°
⇒ 180° – ∠AOB = 90° [ ∠CAO + ∠CBO + ∠AOB = 180°]
⇒ 180° – 90° = ∠AOB
⇒ ∠AOB = 90°.

Question 13.
Last night a big strom hit the city of Cuttack. Wind blow with the speed more than 200 km/hr. Many trees got uprooted, pillars broken. Many places in the city got darken as there was no electricity. An electrician was called to repair the faulty wires. He has to repair an electric fault on a pole of height 5 m. He needs to reach a point 1.3 m below the top of the pole to undertake a repair work as shown in figure.

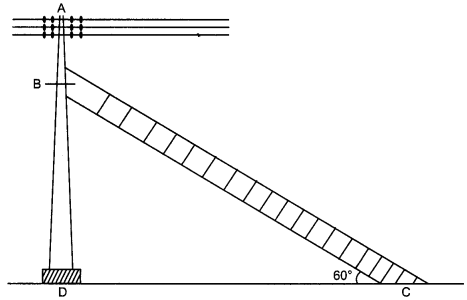
(i) If the ladder is inclined at 60°. Then find the length of the ladder required. (2)
(ii) How far the foot of the ladder should be placed from the foot of the pole? (2)
Answer:
(i) Given, Height of the pole = 5 m
Height to be reached = 5 – 1.3 – 3.7 m
Angle of elevation = 60°
In LBDC,
∴ Length of ladder = BC
\(\sin 60^{\circ}=\frac{\mathrm{BD}}{\mathrm{BC}}\)
⇒ \(\frac{\sqrt{3}}{2}=\frac{3.7}{B C}\)
⇒ BC = \(\frac{3.7 \times 2}{\sqrt{3}}=\frac{7.4}{\sqrt{3}}\)
= \(\frac{7.4}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\)
= \(\frac{7.4 \sqrt{3}}{3}\) m.

(ii)
Distance between foot of the pole and foot of the ladder is DC.
\(\tan 60^{\circ}=\frac{\mathrm{BD}}{\mathrm{DC}}\)
⇒ \(\sqrt{3}=\frac{3.7}{\mathrm{DC}}\)
⇒ \(\mathrm{DC}=\frac{3.7}{\sqrt{3}}\)
⇒ \(\frac{3.7 \times \sqrt{3}}{3}=1.23 \sqrt{3}\) m.

Question 14.
Snehal throws a party in her house. For the party she has to serve snacks and juice to her guests. She has a big jar of diameter 14 cm and height 42 cm filled with juice. She has two type of glasses for serving juice of cylindrical shape. Glass A with diameter 7 cm and height 10 cm and glass B with diameter 7 cm and height 12 cm.
Based on the above information answer the questions that follows :
(i) What is the capacity of juice jar? (2)
(ii) If the juice is to served in glass B. Then how many guest will be served? (2)
Answer:
(i) Since, jar is of cylindrical shape. So the capacity of jar is given by volume of cylinder.
Volume of cylinder = r²h
Radius of jar (r) = \(\frac {14}{2}\) = 7cm
Height of jar (h) = 42 cm
∴ Volume = \(\frac {22}{7}\) x 7 x 7 x 42
= 6,468 cm³.

(ii) Dimensions of glass B are
Radius of glass = \(\frac {7}{2}\) cm
Height of glass = 12 cm
∴ Capacity of each glass = \(\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2} \times 12\)
= 462 cm³
∴ Number of guests served = \(\frac{Volume of juice jar}{Volume of each glass}\)
= \(\frac{6468}{462}\)
= 14.