Selina Concise Mathematics Class 10 ICSE Solutions Chapter 16 Loci (Locus and Its Constructions) Ex 16A
These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 16 Loci (Locus and Its Constructions) Ex 16A
Other Exercises
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 16 Loci (Locus and Its Constructions) Ex 16A
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 16 Loci (Locus and Its Constructions) Ex 16B
Question 1.
Given— PQ is perpendicular bisector of side AB of the triangle ABC
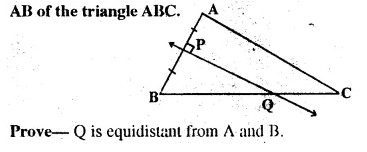
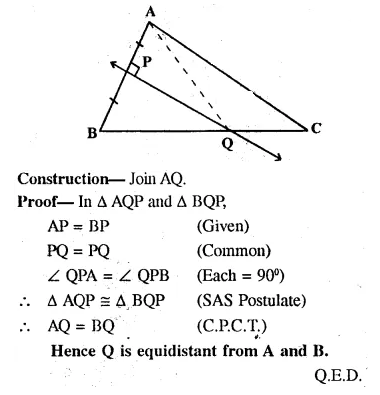
Solution:
Question 2.
Given— CP is bisector of angle C of A ABC.
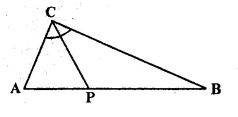
Prove: p is equidistant from AC and BC
Solution:
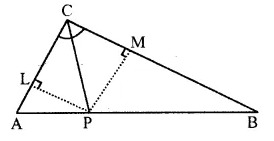

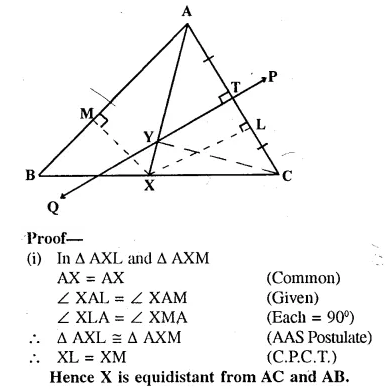
Question 3.
Given— AX bisects angle BAG and PQ is perpendicular bisector of AC which meets AX at point Y.
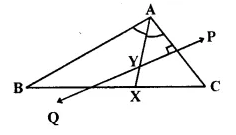
Prove:
(i) X is equidistant from AB and AC.
(ii) Y is equidistant from A and C.
Solution:
Construction: From X, draw XL ⊥ AC and XM ⊥ AB and join YC.

Question 4.
Construct a triangle ABC, in which AB = 4.2 cm, BC = 6.3 cm and AC = 5 cm. Draw perpendicular bisector of BC which meets AC at point D. Prove that D is equidistant from B and C.
Solution:
Given: In Δ ABC, AB, = 4.2 cm, BC = 6.3 cm and AC = 5cm
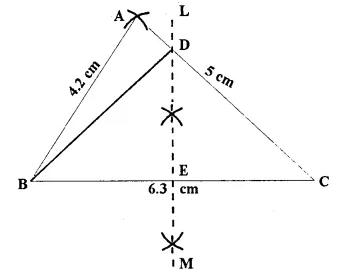
Steps of Construction:
(i) Draw a line segment BC = 6.3 cm.
(ii) With centre B-and radius 4.2 cirr draw mi are.
(iii) With centre C mid radius 5 cm, draw another arc which intersect the first arc at A.
(iv) Join AB mid AC.
A ABC is the required triangle.
(v) Again with centre B mid C mid radius greater
than \(\frac { -1 }{ 2 }\) BC, draw arcs which intersects each other at L mid M.
(vi) Join LM intersecting AC at D mid BC at E.
(vii) Join DB.

Question 5.
In each of the given figures: PA = PH and QA = QB.

Prove, in each case, that PQ (produce, if required) is perpendicular bisector of AB. Hence, state the locus of points equidistant from two given fixed points.
Solution:
(i) Construction: Join PQ which meets AB in D.
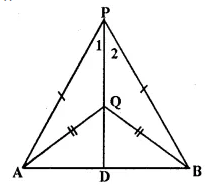
Proof:
P is equidistant from A mid B
∴ P lies on die perpendicular bisector of AB similarly Q is equidistant from A mid B.
∴ Q lies on perpendicular bisector of AB P mid Q both lies on the perpendicular bisector of AB.
∴ PQ is Hie perpendicular bisector of AB
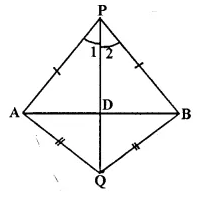
Hence locus of die points which are equidistant from two fixed points, is a perpendicular, bisector of die line joining die fixed points. Q.E.D.
Question 6.
Construct a right angled triangle PQR, in which ∠Q = 90°, hypotenuse PR = 8 cm and QR = 4.5 cm. Draw bisector of angle PQR and let it meets PR at point T. Prove that T is equidistant from PQ and QR.
Solution:
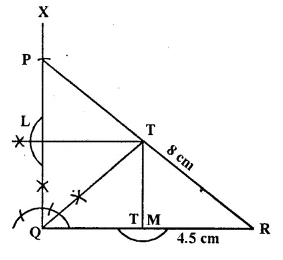
Steps of Construction
(i) Draw a line segment QR = 4.5 cm.
(ii) At Q, draw a ray QX making an angle of 90°.
(iii) With centre P mid radius 8 cm, draw mi arc which intersects QX at P.
(iv) Join RP.
A-PQR is the required triangle.
(v) Draw the bisector of ∠PQR which meets PR in T.
(vi) From T, draw perpendicular PL and PM respec- lively on PQ and QR.

Question 7.
Construct a triangle ABC in which angle ABC = 75°. AB = 5 cm and BC = 6.4 cm.
Draw perpendicular bisector of side BC and also the bisector of angle ACB. If these bisectors intersect each other at point P ; prove that P is equidistant from B and C ; and also from AC and BC.
Solution:
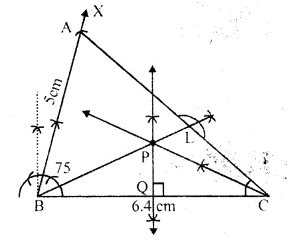
Steps of Construction:
(i) Draw a line segment BC = 6.4 cm.
(ii) At B, draw a ray BX making an angle of 75° with BC and cut off BA = 5 cm.
(iii) Join AC.
Δ ABC is the required triangle.
(iv) Draw the perpendicular bisector of BC.
(v) Draw the angle bisector of ∠ACB which intersects the perpendicular bisector of ,BC at P
(vi) Join PB and draw PL ⊥ AC.

Question 8.
In parallelogram ABCD, side AB is greater than side BC and P is a point in AC such that PB bisects angle B.
Prove that P is equidistant from AB and BC.
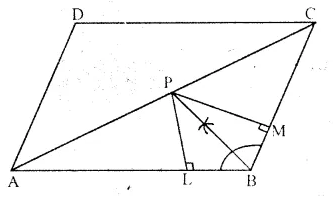
Solution:
Given: In || gm ABCD. AB > BC and bisector of ∠B meets diagonal AC at P.
To Prove: P is equidistant from AB and BC.
Construction: From P, draw PL ⊥ AB and PM ⊥ BC.

Question 9.
In triangle LMN, bisectors of interior angles at L and N intersect each other at point A.
Prove that:
(i) point A is equidistant from all the three sides of the triangle.
(ii) AM bisects angle LMN.
Solution:
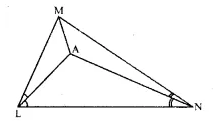
Given: In A LMN, angle bisectors of ∠L and ∠N
meet at A, AM is joined.
To Prove:
(i) A is equidistant from all the sides of A LMN.
(ii) AM is the bisector of ∠M.
Proof: ∴ A lies on the bisector of ∠N
∴ A is equidistant from MN and LN Again
∴ A lies on the bisector of ∠L A is equidistant from LN and LM Hence
∴ A is equidistant from all sides of the triangle LMN.
∴ A lies on the bisector of ∠M Q.E.D.
Question 10.
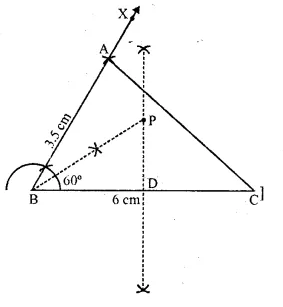
Use ruler and compasses only for this question:
(i) construct ΔABC, where AB = 3.5 cm, BC = 6 cm and ∠ABC = 60°.
(ii) Construct the locus of points inside the triangle which are equidistant from BA and BC.
(iii) Construct the locus of points inside the triangle which are equidistant from B and C.
(iv) Mark the point P which is equidistant from AB, BC and also equidistant from B and C. Measure and record the length of PB. (2010)
Solution:
Steps of construction:
1. Draw a line BC = 6 cm and an angle CBX = 60°. Cut off AB = 3.5 cm. Join AC, ΔABC is the required triangle.
2. Draw ⊥ bisector of BC and bisector of ∠B.
3. Bisector of ∠B meets bisector of BC at P
∴ BP is the required length, where PB = 3.5 cm
4. P is the point which is equidistant from BA and BC, also equidistant fromB and C
Question 11.
The given figure shows a triangle ABC in which AD bisects angle BAC. EG is perpendicular bisector of side AB which intersects AD at point E Prove that:
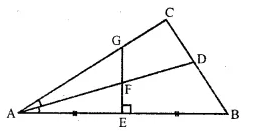
(i) F is equidistant from A and B.
(ii) F is equidistant from AB and AC.
Solution:
Given : In the figure,
In ΔABC, AD is the bisector of ∠BAC Which meets BC at D EG is the perpendicular bisector of AB which intersects AD at F
To prove :
(i) F is equidistant from A and B.
(ii) F is equidistant from AB and AC.
Proof:
(i) ∴ F lies on the perpendicular bisector of AB F is equidistant from A and B
(ii) Again,
∴ F lies onthe bisector of ∠BAC
∴ F is equidistant from AB and AC.
(10 cm theorem)
Hence proved.
Question 12.
The bisectors of ∠B and ∠C of a quadrilateral ABCD intersect each other at point P. Show that P is equidistant from the opposite sides AB and CD.
Solution:
In quadrilateral ABCD, the bisectors of ∠B and ∠C meet each other at P.
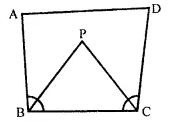
To prove : D is equidistant from the sides AB and CD.
Proof:
∴ P lies on the bisector of ∠B P is equidistant from AB and BC ….(i)
Similarly, P lies on the bisector of ∠C P is equidistant from BC and CD ….(ii)
From (i) and (ii),
∴ P is equidistant from AB and CD
Hence proved.
Question 13.
Draw a line AB = 6 cm. Draw the locus of all the points which are equidistant from A and B.
Solution:
Steps of Construction:
(i) Draw a line segment AB = 6 cm
(ii) Draw perpendicular bisector LM of AB. LM is the required locus.
(iii) Take any point on LM say P.
(iv) Join PA and PB
∵ P lies on the right bisector of line AB
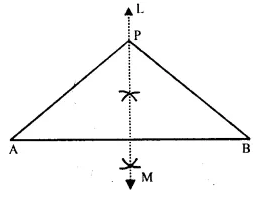
∴ P is equidistant from A and B.
∴ PA = PB
∴ Perpendicular bisector of AB is the locus of all points which are equidistant from A and B.
Question 14.
Draw an angle ABC = 75°. Draw the locus of all the points equidistant from AB and BC.
Solution:
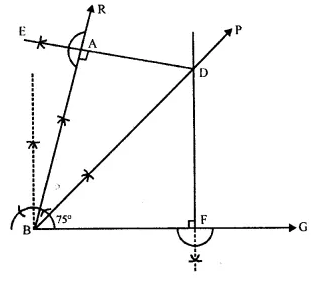
Steps of Construction:
(I) Draw a ray BC.
(ii) Construct a ray RA making an angle of 750 with BC.
(iii) ∴ ∠ABC = 75°
(iv) Draw the angle bisector BP of ∠ABC. BP is the required locus.
(v) Take any point D on BP.
(vi) From D, draw DE ⊥ AB and DF ⊥ BC.
∵ D lies on the angle bisector ∠ABC.
∴ D is equidistant from AB and BC.
∴ DE = DF
Similarly any point on BP, is equidistant from AB and BC.
∴BP is the locus of all points which are equidistant from AB and BC.
Question 15.
Draw an angle ABC = 60°, having AB = 4.6 cm and BC = 5 cm. Find a point P equidistant from AB and BC ; and also equidistant from A and B
Solution:
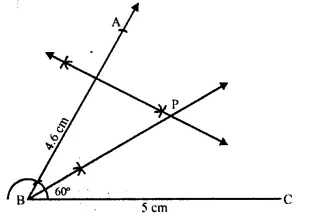
Steps of Construction:
(i) Draw a line segment BC = 5 cm.
(ii) At B, draw a ray BX making an angle of 60° and cut off BA = 4.6 cm.
(iii) Draw the angle bisector of ∠ABC.
(iv) Draw the perpendicular bisector of AB which intersects the angle bisector at P.
P is the required point which is equidistant from AB and BC as well as from points A and B.
Question 16.
In the figure given below, find a point P on CD equidistant from points A and B.

Solution:
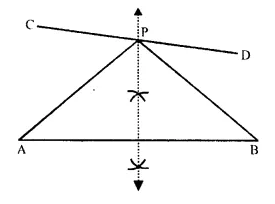
Steps of Construction:
(i) In the figure AB and CD are two line segments.
(ii) Draw the perpendicular bisector of AB which intersects CD in P.
P is the required point which is equidistant from A and B
∵ P lies on the perpendicular bisector of AB.
∴ PA = PB.
Question 17.
In the given triangle ABC, find a point P equidistant from AB and AC; and also equidistant from B and C.
Solution:
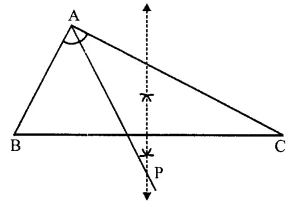
Steps of Construction:
(i) In the given triangle, draw the angle bisector of ∠BAC.
(ii) Draw the perpendicular bisector of BC which intersects the angle bisector of ∠A at P.
P is the required point which is equidistant from AB and AC as well as from B and C.
∵ P lies on the angle bisector of ∠BAC.
∴ It is equidistant from AB and AC. Again
∵ P lies on the perpendicular bisector of BC.
∴ P is equidistant from B and C.
Question 18.
Construct a triangle ABC, with AB = 7 cm, BC = 8 cm and ∠ABC = 60°. Locate by construction the point P such that :
(i) P is equidistant from B and C.
(ii) P is equidistant from AB and BC.
(iii) Measure and record the length of PB.
(2000)
Solution:
Steps of Construction :
1. Draw a line segment AB = 7 cm.
2. Draw angle ∠ABC = 60° with the help of compass.
3. Cut off BC = 8 cm.
4. Join A and C.
5. The triangle ABC so formed is required triangle.
(i) Draw perpendicular bisector of line BC. The point situated on this line will be equidistant from B and C.
(ii) Draw angular bisector of ∠ABC. Any
point situated on this angular bisector is equidistant from lines AB and BC.
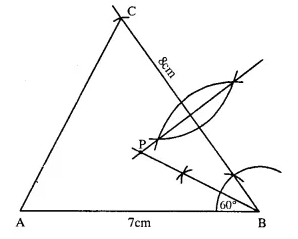
The point which fulfills the condition required in (i) and (ii) is the intersection point of bisector of line BC and angular bisector of ∠ABC.
(iii) Length of PB is 4.5 cm.
Question 19.
On a graph paper, draw the lines x = 3 and y = -5. Now, on the same graph paper, draw the locus of the point which is equidistant from the given lines.
Solution:
On the graph paper, draw axis XOX’ and YOY’ Draw a line l, x = 3 which is parallel to y-axis and another line m, y = -5, which is parallel to x-axis
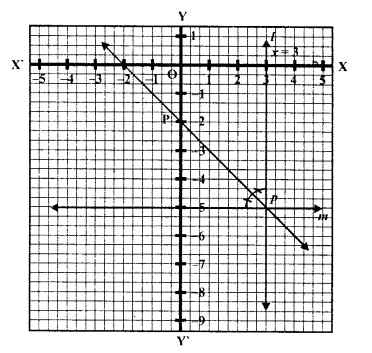
These two lines intersect eachother at P.
Now draw the angle bisector p of ∠P
∵ p is the bisector of ∠P
∴ Any point on P, is equidistant from l and m
∴ This line p is equidistant from l and m.
Question 20.
On a graph paper, draw the line x = 6. Now, on the same graph paper, draw the locus of the point which moves in such a way that its distance from the given line is always equal to 3 units.
Solution:
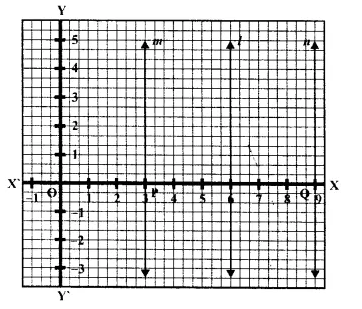
On the graph, draw axis XOX’ and YOY’
Draw a line l, x = 6
Which is parallel to -axis
Take point P and Q which are at a distance of 3units from the line l
Draw line rn and n from P and Q parallel to P respectively
The line m and n are the required locus of the points P and Q
Which arc always 3 units from the line l.
Hence proved.
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 16 Loci (Locus and Its Constructions) Ex 16B are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.