RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3
Other Exercises
- RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.1
- RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.2
- RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3
- RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals VSAQS
- RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals MCQS
Question 1.
In the figure, compute the area of the quadrilateral.
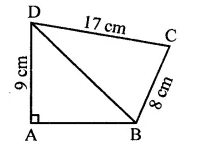
Solution:
In the quadrilateral ABCD,
∠A = 90°, ∠CBD = 90°, AD = 9 cm, BC = 8 cm and CD = 17 cm
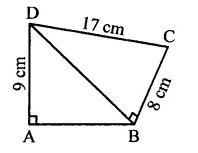
In right ∆BCD,
CD = BC2 + BD2 (Pythagoras Theorem)
⇒ (17)2 = (8)2 + BD2
⇒ 289 = 64 + BD2
⇒ BD2 = 289 – 64 = 225 = (15)2
∴ BD = 15 cm
Now in right ∆ABD,
BD2 = AB2 + AD2
⇒ (15)2 = AB2 + (9)2
⇒ 225 = AB2 + 81
⇒ AB2= 225 – 81 = 144 = (12)2
∴ AB = 12 cm

Question 2.
In the figure, PQRS is a square and T and U are, respectively, the mid-points of PS and QR. Find the area of ∆OTS if PQ = 8 cm.
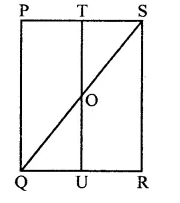
Solution:
In square PQRS, T and U are the mid-points of the sides PS and QR
TU, QS and US are joined
PQ = 8 cm
∴ T and U are mid-points of the opposites sides PS and QR
∴ TU || PQ TO || PQ
In RQS,
T is mid-point of PS and TO || PQ
∴ O is the mid point of SQ 1 1

Question 3.
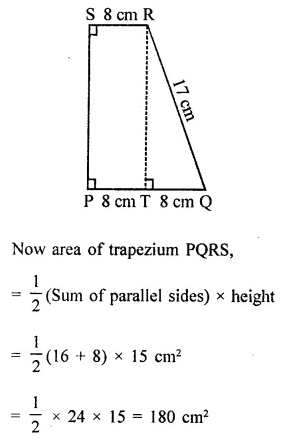
Compute the area of trapezium PQRS in the figure.
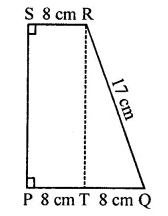
Solution:
In ∆TQR, ∠RTQ = 90°
∴ QR2 = TQ2 + RT2
⇒ (17)2 = (8)2 + RT2
⇒ 289 = 64 + RT2
⇒ RT2 = 289 – 64 = 225 = (15)2
∴ RT = 15 cm
and PQ = 8 + 8 = 16 cm
Question 4.
In the figure, ∠AOB = 90°, AC = BC, OA = 12 cm and OC = 6.5 cm. Find the area of ∆AOB.
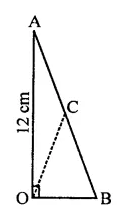
Solution:
In ∆AOB, ∠AOB = 90°
C is a point on AB such that AC = BC Join OC
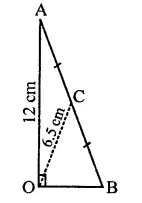
Since C is the mid-point of hypotenuse of right ∆AOB
∴ AC = CB = OC = 6.5 cm
∴ AB = 6.5 + 6.5 = 13 cm
Now in right ∆AOB
⇒ AB2 = AO2 + OB2 (Pythagoras Theorem)
⇒ (13)2 = (12)2 + OB2
⇒ 169 = 144 + OB2
⇒ OB2 = 169 – 144 = 25 = (5)2
∴ OB = 5 cm
Question 5.
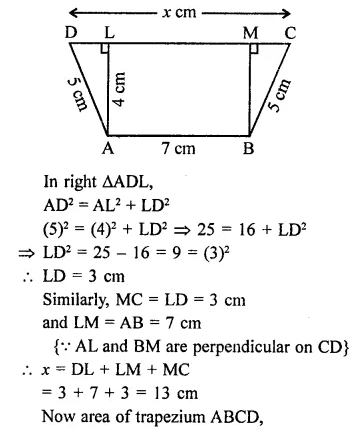
In the figure, ABCD is a trapezium in which AB = 7 cm, AD = BC = 5 cm, DC = x cm, and distance between AB and DC is 4 cm. Find the value of x and area of trapezium ABCD.
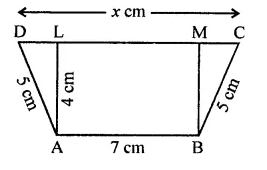
Solution:
In the trapezium ABCD,
AB = 7 cm
AL = BM = 4 cm
AD = BC = 5 cm
Question 6.
In the figure, OCDE is a rectangle inscribed in a quadrant of a circle of radius 10 cm.If OE = 2 \(\sqrt { 5 } \) , find the area of the rectangle.
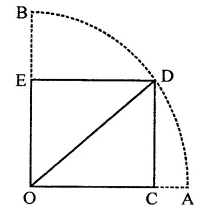
Solution:
Radius of the quadrant of circle = 2\(\sqrt { 5 } \) units
∴ OD diagonal of rectangle = 10 units (∵ OD = OB = OA = 10 cm)
DE = 2 \(\sqrt { 5 } \) cm
∴ In right ∆OED,
OD2 = OE2 + DEv
(10)2 = OE2 + (2\(\sqrt { 5 } \))2
100 = OE2 + 20
OE2 = 100 – 20 = 80
⇒ OE2 = (4\(\sqrt { 5 } \))2
∴ OE = 4\(\sqrt { 5 } \) cm
∴ Area of rectangle = lxb
= DE x OE
= 2\(\sqrt { 5 } \) x 4\(\sqrt { 5 } \)
= 8 x 5 = 40 cm2
Question 7.
In the figure, ABCD is a trapezium in which AB || DC. Prove that ar( ∆AOD = ar(∆BOC).
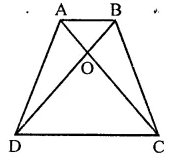
Solution:
In trapezium ABCD, diagonals AC and BD intersect each other at O
∴ ∆ADB and ∆ACB are on the same base AB and between the same parallels
∴ ar(∆ADB = ar(∆ACD)
Subtracting, ar(AAOB) from both sides,
ar(∆ADB) – ar(∆AOB) = ar(∆ACD) – ar(∆AOB)
⇒ ar(∆AOD) = ar(∆BOC)
Question 8.
In the figure, ABCD, ABFE and CDEF are parallelograms. Prove that ar(∆ADE) = ar(∆BCF) [NCERT]
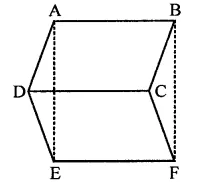
Solution:
Given : In the figure, ABCD, ABEF and CDEF are ||gms
To prove : ar(∆ADE) = ar(∆BCF)
Proof: ∴ ABCD is a ||gm
∴ AD = BC
Similarly, in ||gm ABEF
AE = BF
and in ||gm CDEF,
DE = CF
Now, in ∆ADE and ∆BCF
AD = BC (proved)
DE = CF (proved)
AE = BF (proved)
∴ ∆ADE ≅ ∆BCF
∴ ar(∆ADE) = ar(∆BCF) (∵ Congruent triangles are equal in area)
Question 9.
In the figure, ABC and ABD are two triangles on the base AB. If line segment CD is bisected by AB at O, show that ar(∆ABC) = ar(∆ABC)
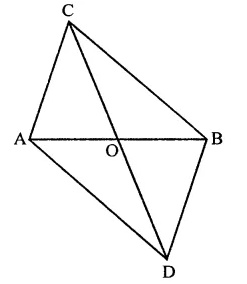
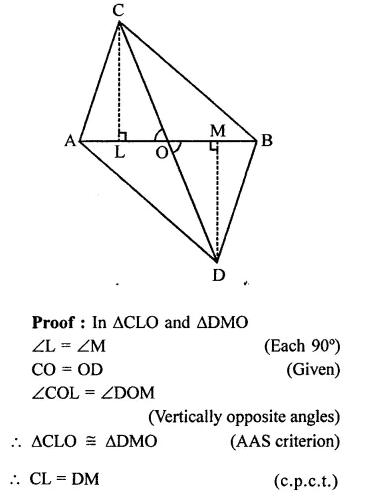
Solution:
Given : In the figure, ∆ABC and ∆ABD are on the same base AB and line CD is bisected by AB at O i.e. CO = OD
To prove : ar(∆ABC) = ar(∆ABD)
Construction : Draw CL ⊥ AB and DM ⊥ AB

Question 10.
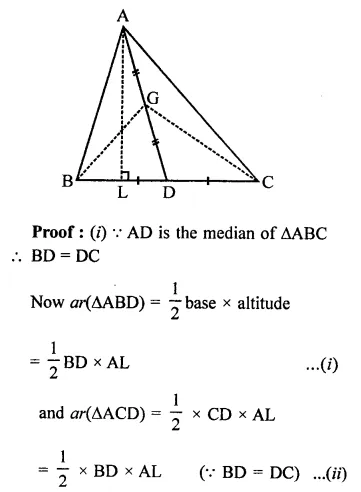
If AD is a median of a triangle ABC, then prove that triangles ADB and ADC are equal in area. If G is the mid point of median AD, prove that ar(∆BGC) = 2ar(∆AGC).
Solution:
Given : In ∆ABC, AD is its median. G is mid point of AD. BG and CF are joined
To prove :
(i) ar(∆ADB) = ar(∆ADC)
(ii) ar(∆BGC) = 2ar(∆AGC)
Construction : Draw AL ⊥ BC

Question 11.
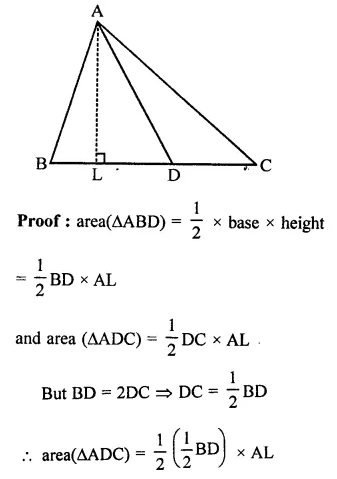
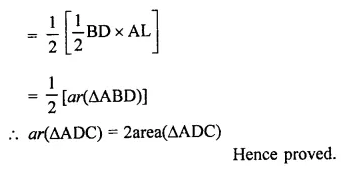
A point D is taken on the side BC of a AABC such that BD = 2DC. Prove that ar(∆ABD) = 2ar(∆ADC)
Solution:
Given : In ∆ABC, D is a point on BC such that
BD = 2DC
AD is joined
To prove : ar(∆ABD) = 2ar(∆ADC)
Construction : Draw AL ⊥ BC
Question 12.
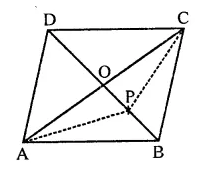
ABCD is a parallelogram whose diagonals intersect at O. If P is any point on BO, prove that
(i) ar(∆ADO) = or (∆CDO)
(ii) ar(∆ABP) = ar(∆CBP).
Solution:
Given : In ||gm ABCD, Diagonals AC and BD intersect each other at O
P is any point on BO
AP and CP are joined
To prove :
(i) ar(∆ADO) = ar(∆CDO)
(ii) ar(∆ABP) = ar(∆CBP)
Proof:
(i) In ∆ADC,
O is the mid point of AC
∴ ar(∆ADO) = ar(∆CDO)
(ii) Since O is the mid point of AC
∴ PO is the median of ∆APC
∴ af(∆APO) = or(∆CPO) …(i)
Similarly, BO is the median of ∆ABC
∴ ar(∆ABO) = ar(∆BCO) …(ii)
Subtracting (i) from (ii),
ar(∆ABO) – ar(∆APO) = ar(∆BCO) – ar( ∆CPO)
⇒ ar(∆ABP) = ar(∆CBP)
Hence proved.
Question 13.
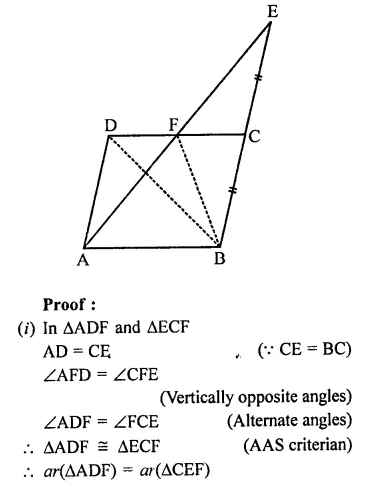
ABCD is a parallelogram in which BC is produced to E such that CE = BC. AE intersects CD at F.
(i) Prove that ar(∆ADF) = ar(∆ECF)
(ii) If the area of ∆DFB = 3 cm2, find the area of ||gm ABCD.
Solution:
Given : In ||gm ABCD, BC is produced to E such that CE = BC
AE intersects CD at F
To prove :
(i) ar(∆ADF) = ar(∆ECF)
(ii) If ar(∆DFB) = 3 cm2, find the area of (||gm ABCD)

Question 14.
ABCD is a parallelogram whose diagonals AC and BD intersect at O. A line through O intersects AB at P and DC at Q. Prove that ar(∆POA) = ar(∆QOC).
Solution:
Given : In ||gm ABCD, diagonals AC and BD intersect at O
A line through O intersects AB at P and CD at Q
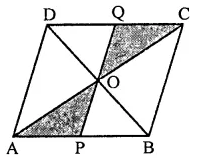
To prove : ar(∆POA) = ar(∆QOC)
Proof : In ∆POA and ∆QOC,
OA = OC (O is mid-point of AC)
∠AOD = ∠COQ (Vertically opposite angles)
∠APO = ∠CQO (Alternate angles)
∴ ar(∆POA) ≅ ar(∆QOC) (AAS criterian)
∴ ar(∆POA) = ar(∆QOC)
Question 15.
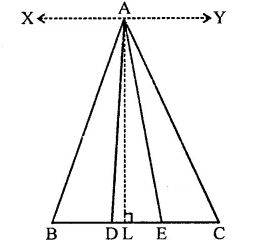
In the figure, D and E are two points on BC such that BD = DE = EC. Show that ar(∆ABD) = ar(∆ADE) = ar(∆AEC). [NCERT]
Solution:
Given : D and E are two points on BC such that BD = DE = EC
AD and AE are joined
To prove : ar(∆ABD) = ar(∆ADE) = ar(∆AEC)
Construction : From A, draw AL ⊥ BC and XAY || BC
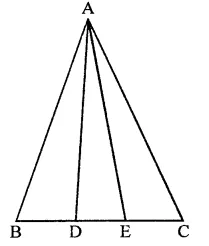
Proof: ∵ BD = DE = EC
and ∆ABD, ∆ADE and ∆AEC have equal bases and from the common vertex A
∴ ar(∆ABD) = ar(∆ADE) = ar(∆AEC)
Question 16.
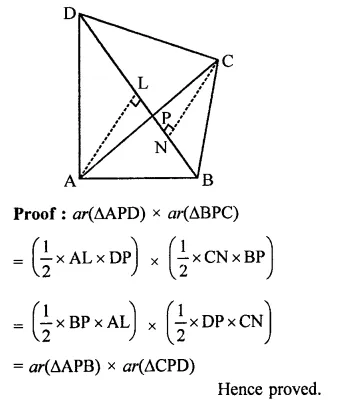
Diagonals AC and BD of a quadrilateral ABCD intersect each other at P.
Show that: ar(∆APB) x ar(∆CPD) = ar(∆APD) x ar(∆BPC)
Solution:
Given : In quadrilateral ABCD, diagonal AC and BD intersect each other as P
To prove : ar(∆APB) x ar(∆CPD) = ar(APD) x ar(∆BPC)
Construction : Draw AL and CN perpendiculars on BD
Question 17.
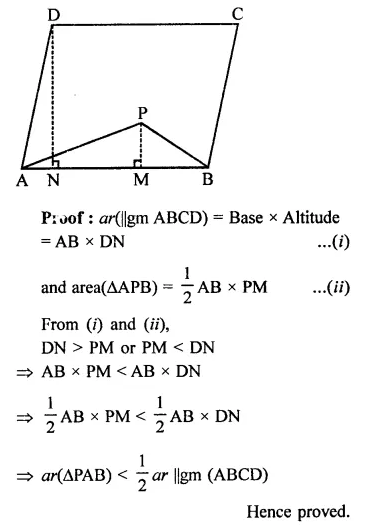
If P is any point in the interior of a parallelogram ABCD, then prove that area of the triangle APB is less than half the area of parallelogram.
Solution:
Given : In ||gm ABCD, P is any point in the ||gm
AP and BP are joined
To prove : ar(∆APB) < \(\frac { 1 }{ 2 }\) ar(||gm ABCD)
Construction : Draw DN ⊥AB and PM ⊥ AM
Question 18.
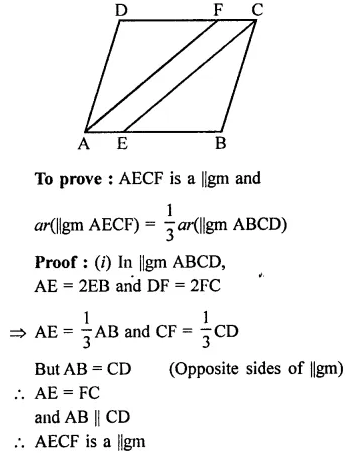
ABCD is a parallelogram. E is a point on BA such that BE = 2EA and F is a point on DC such that DF = 2FC. Prove that AECF is a parallelogram whose area is one third of the area of parallelogram ABCD.
Solution:
Given : In ||gm ABCD, E is a point on AB such that BE = 2EA and F is a point on CD such that DF = 2FC. AE and CE are joined

Question 19.
In a ∆ABC, P and Q are respectively, the mid-points of AB and BC and R is the mid-point of AP. Prove that
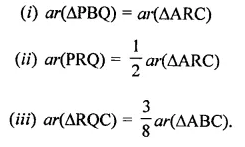
Solution:
Given : In ∆ABC,
P and Q are mid-pionts of AB and BC R is mid-point of AP, PQ, RC, RQ are joined
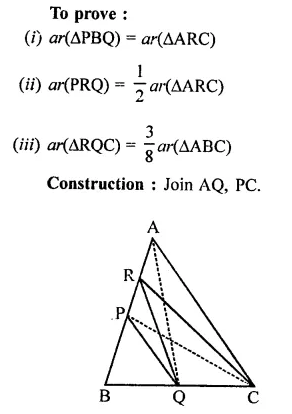



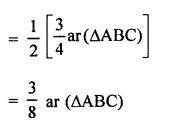
Question 20.
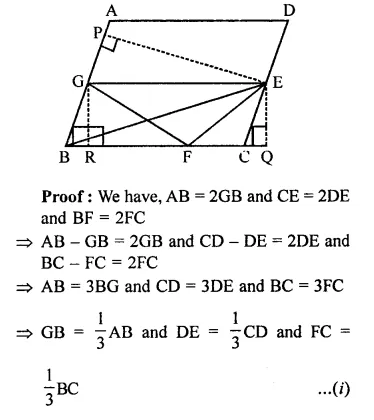
ABCD is a parallelogram, G is the point on AB such that AG = 2GB, E is a point of DC such that CE = 2DE and F is the point of BC such that BF = 2FC. Prove that:
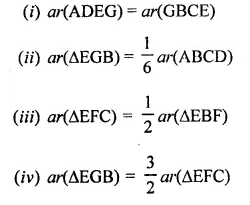
(v) Find what portion of the area of parallelogram is the area of AEFG.
Solution:
Given : ABCD is a parallelogram and AG = 2GB, CE = 2DE and BF = 2FC
To prove :
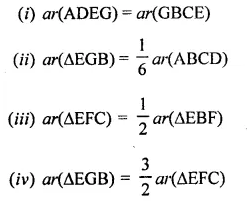
(v) Find what portion of the area of parallelogram is the area of AFEG.
Construction : Draw EP ⊥ AB and EQ ⊥ BC
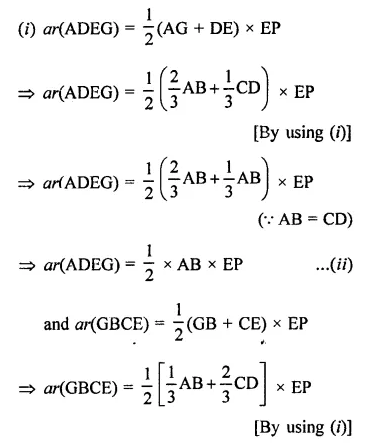
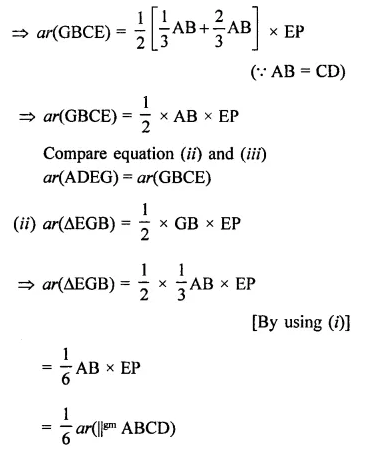
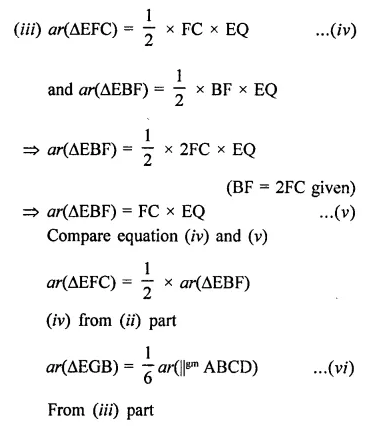
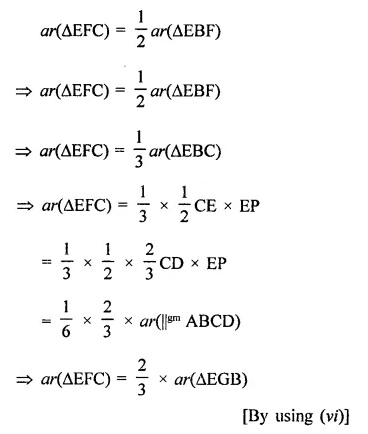

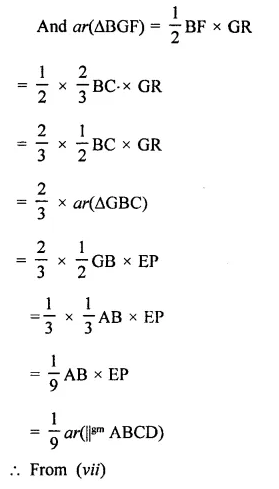
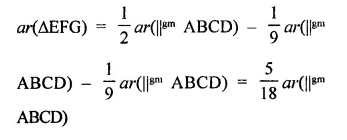
Question 21.
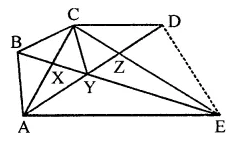
In the figure, CD || AE and CY || BA.
(i) Name a triangle equal in area of ACBX.
(ii) Prove that or(∆ZDE) = ar(∆CZA).
(iii) Prove that ar(∆CZY) = ar(∆EDZ).
Solution:
Given : In the figure,
CP || AE and CY || BA
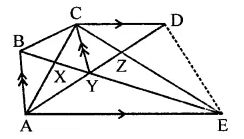
To prove :
(i) Name a triangle equal in area of ∆CBX
(ii) Prove that ar(∆ZDE) = ar(∆CZA)
(iii) ar(BCZY) = ar(∆EDZ)
Proof:
(i) ∆CBX and ∆CYX are on the same base BY and between same parallels.
∴ ar(∆CBX) = ar(∆CYX)
(ii) ∆ADE and ∆ACE are on the same base AE
and between the same parallels (AE || CD)
∴ ar(∆ADE) = ar(∆ACE)
Subtracting ar(∆AZE) from both sides
⇒ ar(∆ADE) – ar(∆AZE) = ar(∆ACE) – ar(∆AZE)
⇒ ar(∆ZDE) = ar(∆ACZ)
⇒ ar∆ZDE = ar∆CZA
(iii) ∵ As ACY and BCY are on the same base CY and between the same parallels
∴ ar(∆ACY) = ar(∆BCY)
Now ar(∆ACZ) = ar(∆ZDE) (Proved)
⇒ ar(∆ACY) + ar(∆CYZ) = ar(∆EDZ)
⇒ ar(∆BCY) + ar(∆CYZ) = ar(∆EDZ)
∴ ar quad. (BCZY) = ar(EDZ)
Hence proved.
Question 22.
In the figure, PSD A is a parallelogram in which PQ = QR = RS and AP || BQ || CR. Prove that ar(∆PQE) = ar(∆CFD).
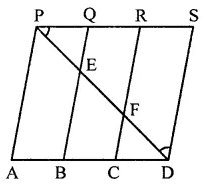
Solution:
Given : In the figure, PSDA is a ||gm in
which PQ = QR = RS and
AP || BQ || CR || DS
To prove : ar(∆PQE) = ar(∆CFD)
Construction : Join PD
Proof : ∵ PA || BQ || CR || DS
and PQ – QR = RS (Given)
∴ AB = BC = CD
∴ PQ = CD
Now in ABED, F is mid point of ED
∴ EF = FD
Similarly, EF = PE
⇒ PE = FD
In ∆PQE and ∆CFD,
∴ ∠EPQ = ∠FDC (Alternate angles)
PQ = CD
PE = FD (Proved)
∴ APQE ≅ ACFD (SAS cirterion)
∴ ar(∆PQE) = ar(∆CFD)
Question 23.
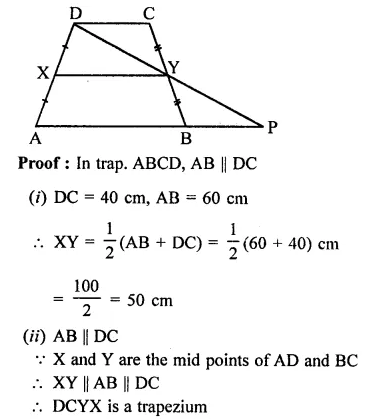
In the figure, ABCD is a trapezium in which AB || DC and DC = 40 cm and AB = 60 cm. If X and Y are, respectively the mid-points of AD and BC, prove that:
(i) XY = 50 cm
(ii) DCYX is a trapezium
(iii) ar(trap. DCYX) = \(\frac { 9 }{ 11 }\) ar(trap. XYBA)
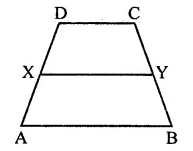
Solution:
Given : In the figure, ABCD is a trapezium in which AB || DC
DC = 40 cm, AB = 60 cm
X and Y are the mid-points of AD and BC respectively
To prove :
(i) XY = 50 cm
(ii) DCYX is a trapezium
(iii) ar(trap. DCYX) = \(\frac { 9 }{ 11 }\) m(trap. XYBA)
Construction : Join DY and produce it to meet AB produced at P

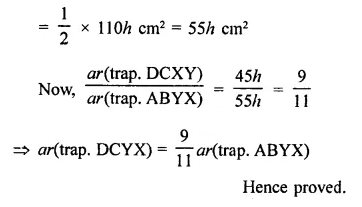
Question 24.
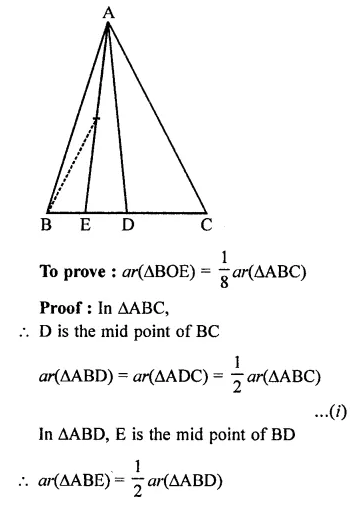
D is the mid-point of side BC of ∆ABC and E is the mid-point of BD. If O is the mid-point of AE, prove that ar(∆BOE) = \(\frac { 1 }{ 8 }\) ar(∆ABC).
Solution:
Given : In ∆ABC, D is mid point of BC, E is mid point BE and O is the mid point of AE. BO, AE, AD are joined.
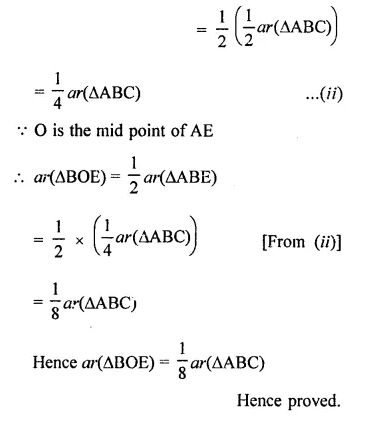
Question 25.
In the figure, X and Y are the mid-points of AC and AB respectively, QP || BC and CYQ and BXP are straight lines. Prove that ar(∆ABP) = ar(∆ACQ).
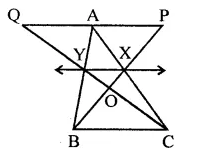
Solution:
Given : In ∆ABC, X and Y are the mid pionts of AC and AB respectively. Through A, a line parallel to BC is drawn. Join BX and CY and produce them to meet the parallel line through A, at P and Q respectively and intersect each other at O.
To prove : ar(∆ABP) = ar(∆ACQ)
Construction : Join XY and produce it to both sides
Proof : ∵ X and Y are mid points of sides AC and AB
∴ XY || BC
Similarly, XY || PQ
∆BXY and ∆CXY are on the same base XY and between the same parallels
∴ ar(∆BXY) = ar(∆CXY) …(i)
Now, trap. XYAP and trap. XYAQ are on the same base XY and between the same parallels
∴ ar(XYAP) = ar(XYAQ) …(ii)
Adding (i) and (ii),
∴ ar(∆BXY) + ar(∆YAP)
= ar(CXY) + ar(XYAQ)
⇒ ar(∆ABP) = ar(∆ACQ)
Question 26.
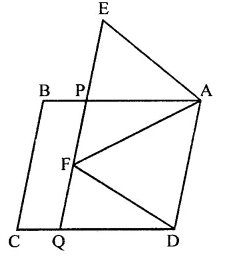
In the figure, ABCD and AEFD are two parallelograms. Prove that
(i) PE = FQ
(ii) ar(∆APE) : ar(∆PFA) = ar(∆QFD) : ar(∆PFD)
(iii) ar(∆PEA) = ar(∆QFD).
Solution:
Given : Two ||gm ABCD and ||gm AEFD are on the same base AD. EF is produced to meet CD at Q. Join AF and PD also
To prove :
(i) PE = FQ
(ii) ar(∆APE) : ar(∆PFA) = ar(∆QFD) : ar(∆PFD)
(iii) ar(∆PEA) = ar(∆QFD)
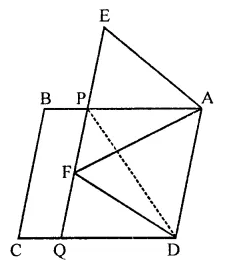
Proof:
(i) In ∆AEP and DFQ,
AE = DF (Opposite sides of a ||gm)
∠AEP = ∠DFQ (Corresponding angles)
∠APE = ∠DQF (Corresponding angles)
∴ ∆AEP ≅ ∆DFQ (AAS axiom)
∴ PE = QF (c.p.c.t.)
(ii) and ar(∆AEP) = ar(∆DFQ) …(i)
(iii) ∵ ∆PFA and ∆PFD are on the same base PF and between the same parallels
∴ ar(∆PFA) = ar(∆PFD) …(ii)
From (i) and (ii),
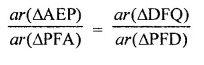
Question 27.
In the figure, ABCD is a ||gm. O is any point on AC. PQ || AB and LM || AD. Prove that ar(||gm DLOP) = ar(||gm BMOQ).
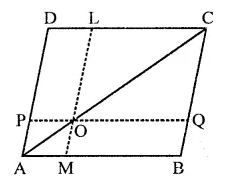
Solution:
Given : In ||gm ABCD, O is any point on diagonal AC. PQ || AB and LM || BC
To prove : ar(||gm DLOP) = ar(||gm BMOQ)
Proof : ∵ Since, a diagonal of a parallelogram divides it into two triangles of equal area.
∴ ar(∆ADC) = or(∆ABC)
⇒ ar(∆APO) + or(||gm DLOP) + ar(∆OLC)
= ar(∆AOM) + ar(||gm BMOQ) + ar( ∆OQC) …(i)
Since, AO and OC are diagonals of parallelograms AMOP and OQCL respectively,
∴ ar(∆APO) = ar(∆AMO) …(ii)
And, ar(∆OLC) = ar(∆OQC) …(Hi)
Subtracting (ii) and (iii) from (i), we get ar(||gm DLOP) = ar(||gm BMOQ)
Question 28.
In a ∆ABC, if L and M are points on AB and AC respectively such that LM || BC.
Prove that:
(i) ar(∆LCM) = ar(∆LBM)
(ii) ar(∆LBC) = ar(∆MBC)
(iii) ar(∆ABM) = ar(∆ACL)
(iv) ar(∆LOB) = ar(∆MOC).
Solution:
Given : In ∆ABC,
L and M are mid points on AB and AC
LM, LC and MB are joined
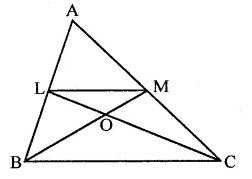
To prove :
(i) ar(∆LCM) = or(∆LBM)
(ii) ar(∆LBC) = ar(∆MBC)
(iii) ar(∆ABM) = ar(∆ACL)
(iv) ar(∆LOB) = ar(∆MOC)
Proof: ∵ L and M are the mid points of AB and AC
∴ LM || BC
(i) Now ∆LBM and ∆LCM are on the same base LM and between the same parallels
∴ar(∆LBM) = ar(∆LCM) …(i)
⇒ ar(∆LCM) = ar(∆LBM)
(ii) ∵ ∆LBC and ∆MBC are on the same base
BC and between the same parallels
∴ ar(∆LBC) = ar(∆MBC) …(ii)
(iii) a(∆LMB) = ar(∆LMC) [From (i)]
⇒ ar(∆ALM) + ar(∆LMB)
= ar(∆ALM) + ar(∆LMC) [Adding or(∆ALM) to both sides]
⇒ ar(∆ABM) = ar(∆ACL)
(iv) ∵ ar(∆LBC) = ar(∆MBC) [From (ii)]
⇒ ar(∆LBC) – ar(∆BOC) = ar(∆MBC) – ar(∆BOC)
ar(∆LBO) = ar(∆MOC)
Question 29.
In the figure, ABC and BDC are two equilateral triangles such that D is the mid-point of BC. AE intersects BC in F.
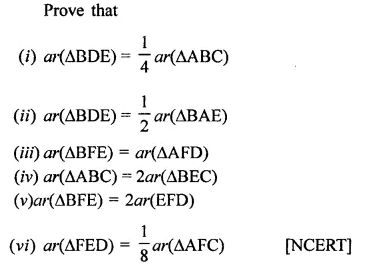
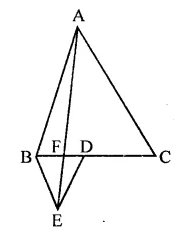
Solution:
Given : ABC and BDE are two equilateral triangles and D is mid point of BC. AE intersects BC in F
To prove :
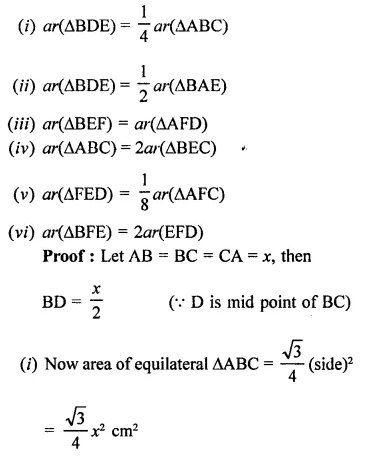





Question 30.
In the figure, ABC is a right triangle right angled at A, BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ⊥ DE meets BC at Y. Show that [NCERT]
(i) ∆MBC ≅ ∆ABD
(ii) ar(BYXD) = ar(∆MBC)
(iii) ar(BYXD) = ar(ABMN)
(iv) ∆FCB ≅ ∆ACE
(v) ar(CYXE) = 2ar(∆FCB)
(vi) ar(CYXE) = ar(∆CFG)
(vii) ar(BCED) = ar(AMBN) + ar(ACFG)
Solution:
Given : In ∆ABC, ∠A = 90°
BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively
AX ⊥ DE meeting DE at X
To prove :
(i) ∆MBC ≅ ∆ABD
(ii) ar(BYXD) = 2ar(∆MBC)
(iii) ar(BYXD) = ar(ABMN)
(iv) ∆FCB ≅ ∆ACE
(v) ar(CYXE) = 2ar(∆FCB)
(vi) ar(CYXE) = ar(ACFG)
(vii) ar(BCED) = or(AMBN) + ar(ACFG)
Construction : Join AD, AE, BF and CM
Proof:
(i) In ∆MBC and ∆ABD,
MB=AB (Sides of square)
BC = BD
∠MBC = ∠ABD (Each angle = 90° + ∠ABC)
∴ ∆MBC ≅ ∆ABD (SAS criterian)
∴ ar(∆MBC) = ar(∆ABD) …(i)
(ii) ∵ ∆ABD and rectangle BYXD are on the same base BD and between the same parallels
∴ ar(∆ABD) = \(\frac { 1 }{ 2 }\) ar(rect. BYXD)
⇒ ar(rect. BYXD) = 2ar(∆ABD)
⇒ ar(rect. BYXD) = 2ar(∆MBC) …(ii)
(iii) Similarly, ∆MBC and square MBAN are on the same base MB and between the same parallels
∴ ar(∆MBC) = ar(sq. ABMN) …(iii)
From (ii) and (iii)
ar(sq. ∆BMN) = ar(rect. BYXD)
(iv) In AFCB and ∆ACE,
FC = AC
CB = CE (Sides of squares)
∠FCB = ∠ACE (Each = 90° + ∠ACB)
∴ ∆FCB = ∆ACE (SAS criterian)
(v) ∵ ∆FCB ≅ ∆ACE (Proved)
∴ ar(∆FCB) = ar(∆ACE)
∵∆ACE and rectangle CYXE are on the same base and between the same parallels
∴ 2ar(∆ACE) = ar(CYXC)
⇒ 2ar(∆FCB) = ar(CYXE) …(iv)
(vi) ∵ AFCB and rectangle FCAG are on the base FC and between the same parallels
∴ 2ar(∆FCB) = ar(FCAG) …(v)
From (iv) and (v)
ar(CMXE) = ar(ACFG)
(vii) In ∆ACB.
BC2 = AB2 + AC2 (By Pythagoras Theorem)
⇒ BC x BD = AB x MB + AC x FC
⇒ ar(BCED) = ar(ABMN) + ar(ACFG)
Hence proved.
Hope given RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.