RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.4
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.4
Other Exercises
- RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.1
- RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.2
- RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.3
- RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.4
- RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.5
- RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.6
- RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula VSAQS
- RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula MCQS
Question 1.
In the figure, it is given that AB = CD and AD = BC. Prove that ∆ADC ≅ ∆CBA.
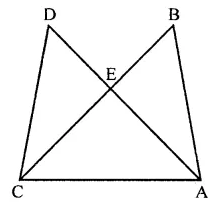
Solution:
Given : In the figure, AB = CD, AD = BC
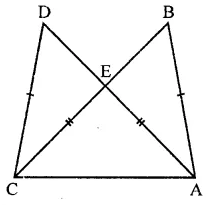
To prove : ∆ADC = ∆CBA
Proof : In ∆ADC and ∆CBA
CD = AB (Given)
AD = BC (Given)
CA = CA (Common)
∴ ∆ADC ≅ ∆CBA (SSS axiom)
Question 2.
In a APQR, if PQ = QR and L, M and N are the mid-points of the sides PQ, QR and RP respectively. Prove that LN = MN.
Solution:
Given : In ∆PQR, PQ = QR
L, M and N are the mid-points of sides PQ, QR and RP respectively. Join LM, MN and LN
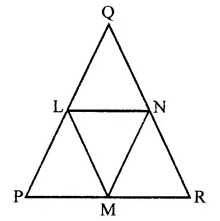
To prove : ∠PNM = ∠PLM
Proof : In ∆PQR,
∵ M and N are the mid points of sides PR and QR respectively
∴ MN || PQ and MN = \(\frac { 1 }{ 2 }\) PQ …(i)
∴ MN = PL
Similarly, we can prove that
LM = PN
Now in ∆NML and ∆LPN
MN = PL (Proved)
LM = PN (Proved)
LN = LN (Common)
∴ ∆NML = ∆LPN (SSS axiom)
∴ ∠MNL = ∠PLN (c.p.c.t.)
and ∠MLN = ∠LNP (c.p.c.t.)
⇒ ∠MNL = ∠LNP = ∠PLM = ∠MLN
⇒ ∠PNM = ∠PLM
Hope given RD Sharma Class 9 Solutions Chapter 12 Heron’s Formula Ex 12.4 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.