RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.5
These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.5
Other Exercises
- RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.1
- RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.2
- RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.3
- RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4
- RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.5
- RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.6
- RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7
- RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.8
- RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.9
Question 1.
Find the square root of each of the long division method.
(I) 12544
(ii) 97344
(iii) 286225
(iv) 390625
(v) 363609
(vi) 974169
(vii) 120409
(viii) 1471369
(ix) 291600
(x) 9653449
(xi) 1745041
(xii) 4008004
(xiii) 20657025
(xiv) 152547201
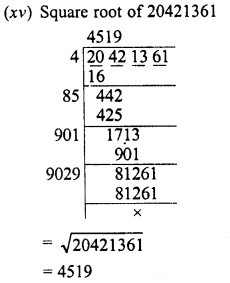
(jcv) 20421361
(xvi) 62504836
(xvii) 82264900
(xviii) 3226694416
(xix)6407522209
(xx) 3915380329
Solution:
<







Question 2.
Find the least number which must be subtracted from the following numbers to make them a perfect square :
(i) 2361
(ii) 194491
(iii) 26535
(iv) 16160
(v) 4401624
Solution:
(i) 2361
Finding the square root of 2361
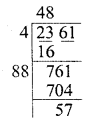
We get 48 as quotient and remainder = 57
∴ To make it a perfect square, we have to subtract 57 from 2361
∴ Least number to be subtracted = 57
(ii) 194491
Finding the square root of 194491
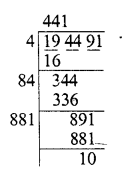
We get 441 as quotient and remainder = 10
∴ To make it a perfect square, we have to subtract 10 from 194491
∴ Least number to be subtracted = 10
(iii) 26535
Finding the square root of 26535
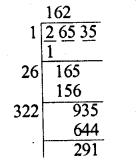
We get 162 as quotient and 291 as remainder
∴ To make it a perfect square, we have to subtract 291 from 26535
∴ Least number to be subtracted = 291
(iv)16160
Finding the square root of 16160
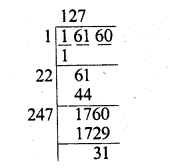
We get 127 as quotient and 31 as remainder
∴ To make it a perfect square, we have to subtract 31 from 16160
∴ Least number to be subtracted = 31
(v) 4401624
Find the square root of 4401624
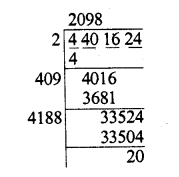
We get 2098 as quotient and 20 as remainder
∴ To make it a perfect square, we have to subtract 20 from 4401624
∴ Least number to be subtracted = 20
Question 3.
Find the least number which must be added to the following numbers to make them a perfect square :
(i) 5607
(ii) 4931
(iii) 4515600
(iv) 37460
(v) 506900
Solution:
(i) 5607
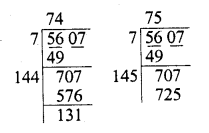
Finding the square root of 5607, we see that 742 = 5607- 131 =5476 and 752 = 5625
∴ 5476 < 5607 < 5625
∴ 5625 – 5607 = 18 is to be added to get a perfect square
∴ Least number to be added = 18
(ii) 4931
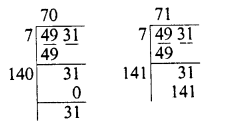
Finding the square root of 4931, we see that 702= 4900
∴ 712 = 5041 4900 <4931 <5041
∴ 5041 – 4931 = 110 is to be added to get a perfect square.
∴ Least number to be added =110
(iii) 4515600
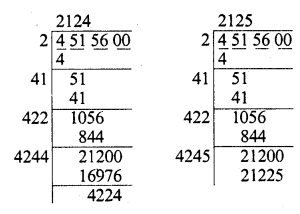
Finding the square root of 4515600, we see
that 21242 = 4511376
and 2 1 252 = 45 1 56 25
∴ 4511376 <4515600 <4515625
∴ 4515625 – 4515600 = 25 is to be added to get a perfect square.
∴ Least number to be added = 25
(iv) 37460
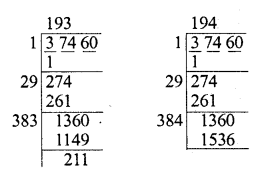
Finding the square root of 37460
that 1932 = 37249, 1942 = =37636
∴ 37249 < 37460 < 37636
∴ 37636 – 37460 = 176 is to be added to get a perfect square.
∴ Least number to be added =176
(v) 506900
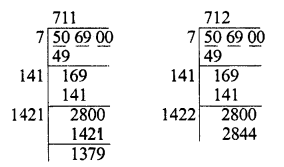
Finding the square root of 506900, we see that
7112 = 505521, 7122 = 506944
∴ 505521 < 506900 < 506944
∴ 506944 – 506900 = 44 is to be added to get a perfect square.
∴ Least number to be added = 44
Question 4.
Find the greatest number of 5 digits which is a perfect square.
Solution:
Greatest number of 5-digits = 99999 Finding square root, we see that 143 is left as remainder
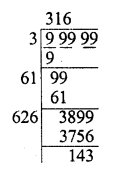
∴ Perfect square = 99999 – 143 = 99856 If we add 1 to 99999, it will because a number of 6 digits
∴ Greatest square 5-digits perfect square = 99856
Question 5.
Find the least number of four digits which is a perfect square.
Solution:
Least number of 4-digits = 10000
Finding square root of 1000
We see that if we subtract 39
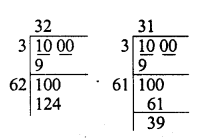
From 1000, we get three digit number
∴ We shall add 124 – 100 = 24 to 1000 to get a
perfect square of 4-digit number
∴ 1000 + 24 = 1024
∴ Least number of 4-digits which is a perfect square = 1024
Question 6.
Find the least number of six-digits which is a perfect square.
Solution:
Least number of 6-digits = 100000
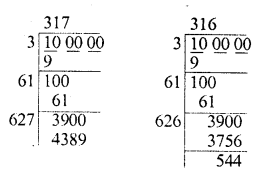
Finding the square root of 100000, we see that if we subtract 544, we get a perfect square of 5-digits.
So we shall add
4389 – 3900 = 489
to 100000 to get a perfect square
Past perfect square of six digits= 100000 + 489 =100489
Question 7.
Find the greatest number of 4-digits which is a perfect square.
Solution:
Greatest number of 4-digits = 9999
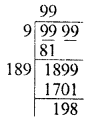
Finding the square root, we see that 198 has been left as remainder
∴ 4-digit greatest perfect square = 9999 – 198 = 9801
Question 8.
A General arranges his soldiers in rows to form a perfect square. He finds that in doing so, 60 soldiers are left out. If the total number of soldiers be 8160, find the number of soldiers in each row.
Solution:
Total number of soldiers = 8160 Soldiers left after arranging them in a square = 60
∴ Number of soldiers which are standing in a square = 8160 – 60 = 8100
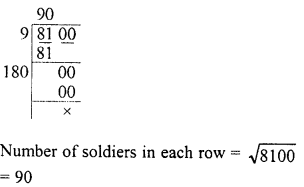
Question 9.
The area of a square field is 60025 m2. A man cycle along its boundry at 18 km/hr. In how much time will be return at the starting point.
Solution:
Area of a square field = 60025 m2

Question 10.
The cost of levelling and turfing a square lawn at Rs. 250 per m2 is Rs. 13322.50. Find the cost of fencing it at Rs. 5 per metre ?
Solution:
Cost of levelling a square field = Rs. 13322.50
Rate of levelling = Rs. 2.50 per m2
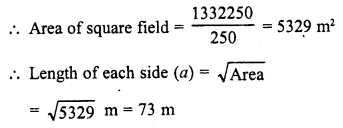
and perimeter = 4a = 4 x 73 = 292 m Rate of fencing the field = Rs. 5 per m
∴ Total cost of fencing = Rs. 5 x 292 = Rs. 1460
Question 11.
Find the greatest number of three digits which is a perfect square.
Solution:
3-digits greatest number = 999
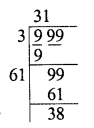
Finding the square root, we see that 38 has been left
∴ Perfect square = 999 – 38 = 961
∴ Greatest 3-digit perfect square = 961
Question 12.
Find the smallest number which must be added to 2300 so that it becomes a perfect square.
Solution:
Finding the square root of 2300
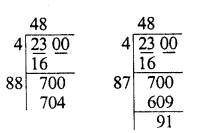
We see that we have to add 704 – 700 = 4 to 2300 in order to get a perfect square
∴ Smallest number to be added = 4
Hope given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.5 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.