RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.2
These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.2
Other Exercises
- RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.1
- RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.2
- RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.3
- RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4
- RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.5
- RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.6
- RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7
- RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.8
- RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.9
Question 1.
The following numbers are not perfect squares. Give reason :
(i) 1547
(ii) 45743
(iii) 8948
(iv) 333333
Solution:
We know that if the units digit is 2, 3, 7 or 8 of a number, then the number is not a perfect square.
(i) ∴ 1547 has 7 as units digit.
∴ It is not a perfect square.
(ii) 45743 has 3 as units digit
∴ It is not a perfect square.
(iii) ∴ 8948 has 8 as units digit
∴ It is not a perfect square.
(iv) ∴ 333333 has 3 as units digits
∴ It is not a perfect square.
Question 2.
Show that the following numbers are not perfect squares :
(i) 9327
(ii) 4058
(iii) 22453
(iv) 743522
Solution:
(i) 9327
∴ The units digit of 9327 is 7
∴ This number can’t be a perfect square.
(ii) 4058
∴ The units digit of 4058 is 8
∴ This number can’t be a perfect square.
(iii) 22453
∴ The units digit of 22453 is 3
.∴ This number can’t be a perfect square.
(iv) 743522
∴ The units digit of 743522 is 2
∴ This number can’t be a perfect square.
Question 3.
The square of which of the following numbers would be an odd number ?
(i) 731
(ii) 3456
(iii) 5559
(iv) 42008
Solution:
We know that the square of an odd number is odd and of even number is even. Therefore
(i) Square of 731 would be odd as it is an odd number.
(ii) Square of 3456 should be even as it is an even number.
(iii) Square of 5559 would be odd as it is an odd number.
(iv) The square of 42008 would be an even number as it is an even number.
Therefore suqares of (i) 731 and (ii) 5559 will be odd numbers.
Question 4.
What will be the units digit of the squares of the following numbers ?
(i) 52
(ii) 977
(iii) 4583
(iv) 78367
(v) 52698
(vi) 99880
(vii) 12796
(viii) 55555
(ix) 53924
Solution:
(i) Square of 52 will be 2704 or (2)2 = 4
∴ Its units digit is 4.
(ii) Square of 977 will be 954529 or (7)2 = 49 .
∴ Its units digit is 9
(iii) Square of 4583 will be 21003889 or (3)2 = 9
∴ Its units digit is 9
(iv) IS 78367, square of 7 = 72 = 49
∴ Its units digit is 9
(v) In 52698, square of 8 = (8)2 = 64
∴ Its units digit is 4
(vi) In 99880, square of 0 = 02 = 0
∴ Its units digit is 0
(vii) In 12796, square of 6 = 62 = 36
∴ Its units digit is 6
(viii) In In 55555, square of 5 = 52 = 25
∴ Its units digit is 5
(ix) In 53924, square pf 4 = 42 = 16
∴ Its units digit is 6
Question 5.
Observe the following pattern
1 + 3 = 22
1 + 3 + 5 = 32
1+34-5 + 7 = 42
and write the value of 1 + 3 + 5 + 7 + 9 +…………upto n terms.
Solution:
The given pattern is
1 + 3 = 22
1 + 3 + 5 = 32
1+3 + 5 + 7 = 42
1+3 + 5 + 7 + 9 +……………… upto n terms (number of terms)2 = n2
Question 6.
Observe the following pattern :
22 – 12 = 2 + 1
32 – 22 = 3 + 2
42 – 32 = 4 + 3
52 – 42 = 5 + 4
Find the value of
(i) 1002 – 992
(ii) 1112 – 1092
(iii) 992 – 962
Solution:
From the given pattern,
22 – 12 = 2 + 1
32 – 22 = 3 + 2
42 – 32 = 4 + 3
52 – 42 = 5 + 4
Therefore
(i) 1002-99° = 100 + 99
(ii) 1112 – 1092 = 1112 – 1102– 1092
= (1112 – 1102) + (1102 – 1092)
= (111 + 110) + (110+ 109)
= 221 + 219 = 440
(iii) 992 – 962 = 992 – 982 + 982 – 972 + 972 – 962
= (992 – 982) + (982 – 972) + (972 – 962)
= (99 + 98) + (98 + 97) + (97 + 96)
= 197 + 195 + 193 = 585
Question 7.
Which of the following triplets are Pythagorean ?
(i) (8, 15, 17)
(ii) (18, 80, 82)
(iii) (14, 48, 51)
(iv) (10, 24, 26)
(vi) (16, 63, 65)
(vii) (12, 35, 38)
Solution:
A pythagorean triplet is possible if (greatest number)2 = (sum of the two smaller numbers)
(i) 8, 15, 17
Here, greatest number =17
∴ (17)2 = 289
and (8)2 + (15)2 = 64 + 225 = 289
∴ 82 + 152 = 172
∴ 8, 15, 17 is a pythagorean triplet
(ii) 18, 80, 82
Greatest number = 82
∴ (82)2 = 6724
and 182 + 802 = 324 + 6400 = 6724
∴ 182 + 802 = 822
∴ 18, 80, 82 is a pythagorean triplet
(iii) 14, 48, 51
Greatest number = 51
∴ (51)2 = 2601
and 142 + 482 = 196 + 2304 = 25 00
∴ 512≠ 142 + 482
∴ 14, 48, 51 is not a pythagorean triplet
(iv) 10, 24, 26
Greatest number is 26
∴ 262 = 676
and 102 + 242 = 100 + 576 = 676
∴ 262 = 102 + 242
∴ 10, 24, 26 is a pythagorean triplet
(vi) 16, 63, 65
Greatest number = 65
∴ 652 = 4225
and 162 + 632 = 256 + 3969 = 4225
∴ 652 = 162 + 632
∴ 16, 63, 65 is a pythagorean triplet
(vii) 12, 35, 38
Greatest number = 38
∴ 382 = 1444
and 122 + 352 = 144 + 1225 = 1369
∴ 382 ≠122 + 352
∴ 12, 35, 38 is not a pythagorean triplet.
Question 8.
Observe the following pattern
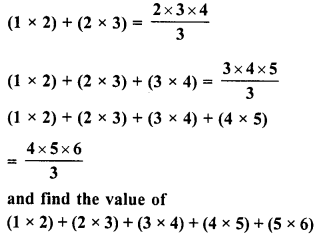
Solution:
From the given pattern
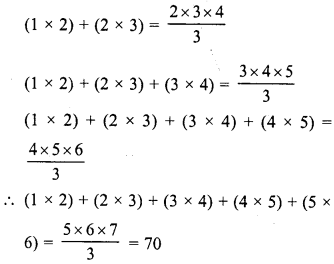
Question 9.
Observe the following pattern
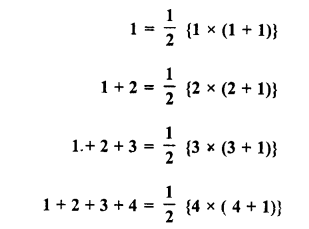
and find the values of each of the following :
(i) 1 + 2 + 3 + 4 + 5 +….. + 50
(ii) 31 + 32 +… + 50
Solution:
From the given pattern,
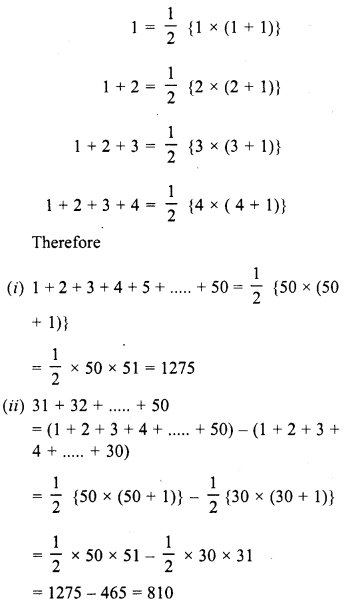
Question 10.
Observe the following pattern
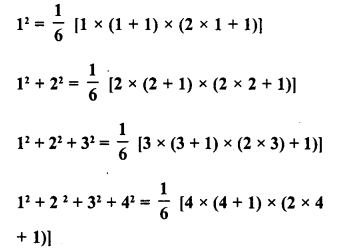
and find the values of each of the following :
(i) 12 + 22 + 32 + 42 +…………… + 102
(ii) 52 + 62 + 72 + 82 + 92 + 102 + 122
Solution:
From the given pattern,
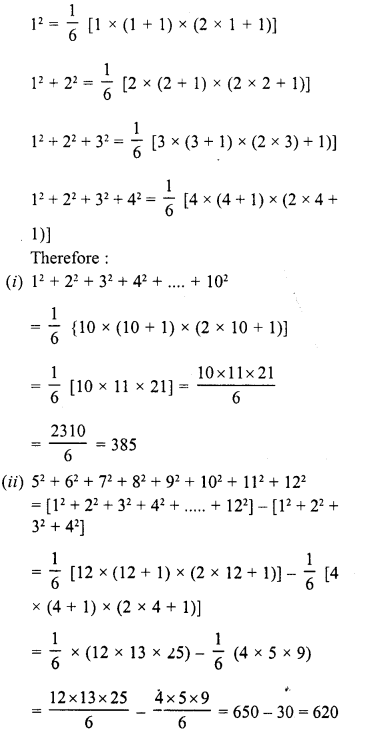
Question 11.
Which of the following numbers are squares of even numbers ?
121,225,256,324,1296,6561,5476,4489, 373758
Solution:
We know that squares of even numbers is also are even number. Therefore numbers 256, 324,1296, 5476 and 373758 have their units digit an even number.
∴ These are the squares of even numbers.
Question 12.
By just examining the units digits, can you tell which of the following cannot be whole squares ?
- 1026
- 1028
- 1024
- 1022
- 1023
- 1027
Solution:
We know that a perfect square cam at ends with the digit 2, 3, 7, or 8
∴ By examining the given number, we can say that 1028, 1022, 1023, 1027 can not be perfect squares.
Question 13.
Write five numbers for which you cannot decide whether they are squares.
Solution:
A number which ends with 1,4, 5, 6, 9 or 0
can’t be a perfect square
2036, 4225, 4881, 5764, 3349, 6400
Question 14.
Write five numbers which you cannot decide whether they are square just by looking at the unit’s digit.
Solution:
A number which does not end with 2, 3, 7 or 8 can be a perfect square
∴ The five numbers can be 2024, 3036, 4069, 3021, 4900
Question 15.
Write true (T) or false (F) for the following statements.
(i) The number of digits in a square number is even.
(ii) The square of a prime number is prime.
(iii) The sum of two square numbers is a square number.
(iv) The difference of two square numbers is a square number.
(vi) The product of two square numbers is a square number.
(vii) No square number is negative.
(viii) There is not square number between 50 and 60.
(ix) There are fourteen square number upto 200.
Solution:
(i) False : In a square number, there is no condition of even or odd digits.
(ii) False : A square of a prime is not a prime.
(iii) False : It is not necessarily.
(iv) False : It is not necessarily.
(vi) True.
(vii) True : A square is always positive.
(viii) True : As 72 = 49, and 82 = 64.
(ix) True : As squares upto 200 are 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196 which are fourteen in numbers.
Hope given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.2 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.