RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS
These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS
Other Exercises
- RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.1
- RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.2
- RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.3
- RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.4
- RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry Ex 6.5
- RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry VSAQS
- RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS
Mark the correct alternative in each of the following :
Question 1.
The distance between the points (cosθ, sinθ) and (sinθ, -cosθ) is
(a) √3
(b) √2
(c) 2
(d) 1
Solution:
(b) Distance between (cosθ, sinθ) and (sinθ, -cosθ)
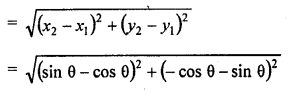
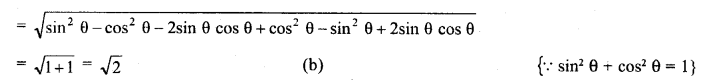
Question 2.
The distance between the points (a cos 25°, 0) and (0, a cos 65°) is
(a) a
(b) 2a
(c) 3a
(d) None of these
Solution:
(a) Distance between (a cos 25°, 0) and (0, a cos 65°)
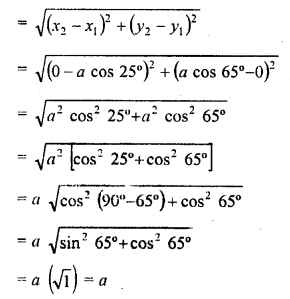
Question 3.
If x is a positive integer such that the distance between points P (x, 2) and Q (3, -6) is 10 units, then x =
(a) 3
(b) -3
(c) 9
(d) -9
Solution:
(c) Distance between P (x, 2) and Q (3, -6) = 10 units
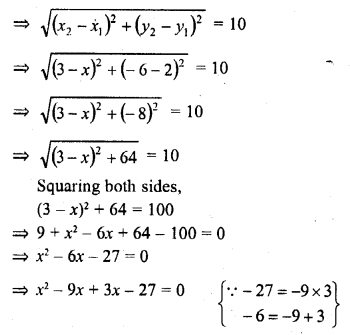
=> x (x – 9) + 3 (x – 9) = 0
(x – 9) (x + 3) = 0
Either x – 9 = 0, then x = 9 or x + 3 = 0, then x = -3
x is positive integer
Hence x = 9
Question 4.
The distance between the points (a cosθ + b sinθ, 0) and (0, a sinθ – b cosθ) is
(a) a² + b²
(b) a + b
(c) a² – b²
(d) √(a²+b²)
Solution:
(d) Distance between (a cosθ + b sinθ, 0) and (0, a sinθ – b cosθ)
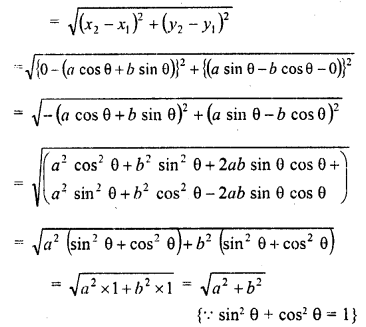
Question 5.
If the distance between the points (4, p) and (1, 0) is 5, then p =
(a) ±4
(b) 4
(c) -4
(d) 0
Solution:
(a) Distance between (4, p) and (1, 0) = 5
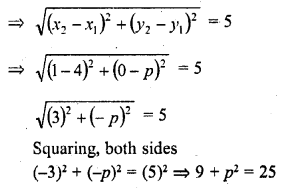
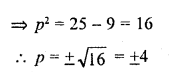
Question 6.
A line segment is of length 10 units. If the coordinates of its one end are (2, -3) and the abscissa of the other end is 10, then its ordinate is
(a) 9, 6
(b) 3, -9
(c) -3, 9
(d) 9, -6
Solution:
(b) Let the ordinate of other end = y
then distance between (2, -3) and (10, y) = 10 units
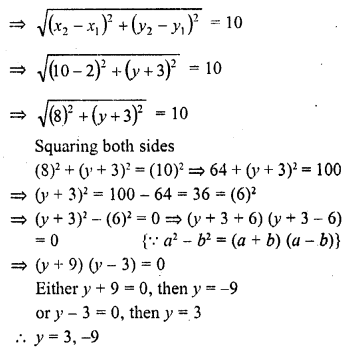
Question 7.
The perimeter of the triangle formed by the points (0, 0), (1, 0) and (0, 1) is
(a) 1 ± √2
(b) √2 + 1
(c) 3
(d) 2 + √2
Solution:
(d) Let the vertices of ∆ABC be A (0, 0), B(1, 0) and C (0, 1)
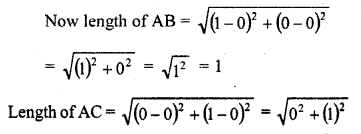
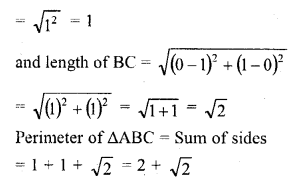
Question 8.
If A (2, 2), B (-4, -4) and C (5, -8) are the vertices of a triangle, then the length of the median through vertices C is
(a) √65
(b) √117
(c) √85
(d) √113
Solution:
(c) Let mid point of A (2, 2), B (-4, -4) be D whose coordinates will be
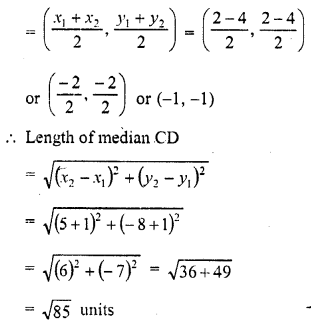
Question 9.
If three points (0, 0), (3, √3) and (3, λ) form an equilateral triangle, then λ =
(a) 2
(b) -3
(c) -4
(d) None of these
Solution:
(d) Let the points (0, 0), (3, √3) and (3, λ) from an equilateral triangle
AB = BC = CA
=> AB² = BC² = CA²
Now, AB² = (x2 – x1)² + (y2 – y1)²
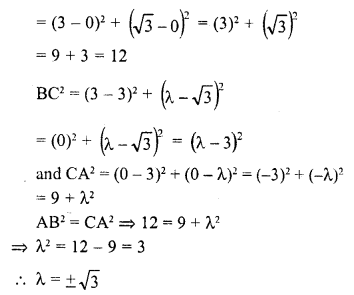
Question 10.
If the points (k, 2k), (3k, 3k) and (3, 1) are collinear, then k
(a) \(\frac { 1 }{ 3 }\)
(b) \(\frac { -1 }{ 3 }\)
(c) \(\frac { 2 }{ 3 }\)
(d) \(\frac { -2 }{ 3 }\)
Solution:
(b) Let the points A (k, 2k), B (3k, 3k) and C (3, 1) be the vertices of a ∆ABC
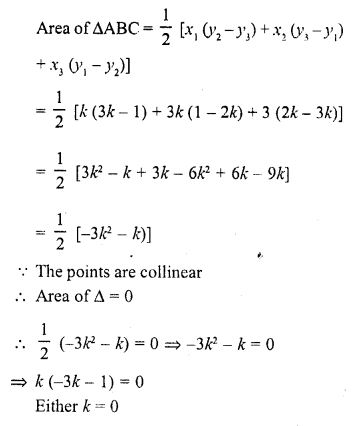
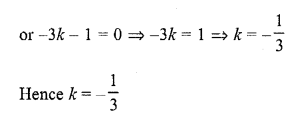
Question 11.
The coordinates of the point on x-axis which are equidistant from the points (-3, 4) and (2, 5) are
(a) (20, 0)
(b) (-23, 0)
(c) (\(\frac { 4 }{ 5 }\) , 0)
(d) None of these
Solution:
(d)

Question 12.
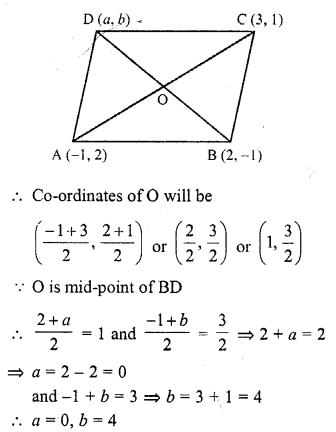
If (-1, 2), (2, -1) and (3, 1) are any three vertices of a parallelogram, then
(a) a = 2, b = 0
(b) a = -2, b = 0
(c) a = -2, b = 6
(d) a = 0, b = 4
Solution:
(d) In ||gm ABCD, diagonals AC and AD bisect each other at O
O is mid-point of AC
Question 13.
If A (5, 3), B (11, -5) and P (12, y) are the vertices of a right triangle right angled at P, then y =
(a) -2, 4
(b) -2, 4
(c) 2, -4
(d) 2, 4
Solution:
(c) A (5, 3), B (11, -5) and P (12, y) are the vertices of a right triangle, right angle at P

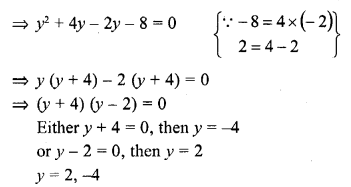
Question 14.
The area of the triangle formed by (a, b + c), (b, c + a) and (c, a + b) is
(a) a + b + c
(b) abc
(c) (a + b + c)²
(d) 0
Solution:
(d) Vertices of a triangle are (a, b + c), (b, c + a) and (c, a + b)
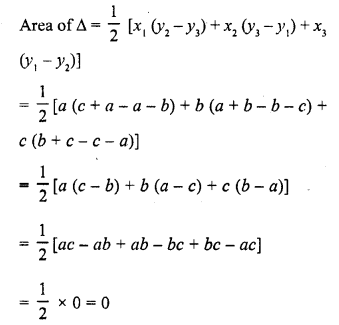
Question 15.
If (x, 2), (-3, -4) and (7, -5) are coliinear, then x =
(a) 60
(b) 63
(c) -63
(d) -60
Solution:
(c) Area of triangle whose vertices are (x, 2), (-3, -4) and (7, -5)
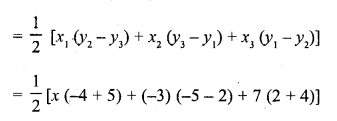
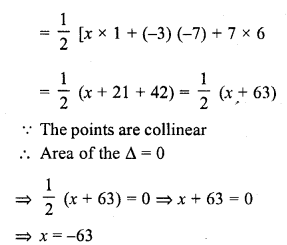
Question 16.
If points (t, 2t), (-2, 6) and (3, 1) are collinear, then t =
(a) \(\frac { 3 }{ 4 }\)
(b) \(\frac { 4 }{ 3 }\)
(c) \(\frac { 5 }{ 3 }\)
(d) \(\frac { 3 }{ 5 }\)
Solution:
(b) The area of triangle whose vertices are (t, 2t), (-2, 6) and (3, 1)
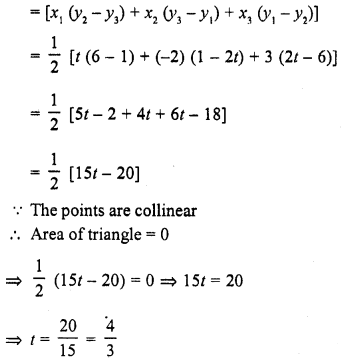
Question 17.
If the area of the triangle formed by the points (x, 2x), (-2, 6) and (3, 1) is 5 square units, then x =
(a) \(\frac { 2 }{ 3 }\)
(b) \(\frac { 3 }{ 5 }\)
(c) 2
(d) 5
Solution:
(c) Area of triangle whose vertices are (x, 2x), (-2, 6) and (3, 1)
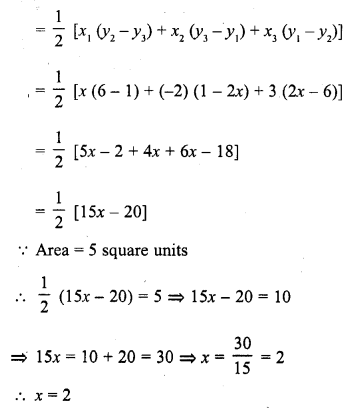
Question 18.
If points (a, 0), (0, b) and (1, 1) are collinear, then \(\frac { 1 }{ a }\) + \(\frac { 1 }{ b }\) =
(a) 1
(b) 2
(c) 0
(d) -1
Solution:
(a) The area of triangle whose vertices are (a, 0), (0, b) and (1, 1)
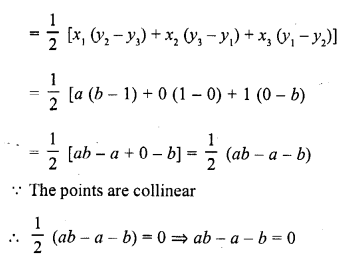
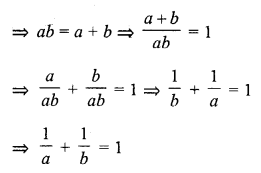
Question 19.
If the centroid of a triangle is (1, 4) and two of its vertices are (4, -3) and (-9, 7), then the area of the triangle is
(a) 183 sq. units
(b) \(\frac { 183 }{ 2 }\) sq. units
(c) 366 sq. units
(d) \(\frac { 183 }{ 4 }\) sq. units
Solution:
(b) Centroid of a triangle = (1, 4)
and two vertices of the triangle are (4, -3) and (-9, 7)
Let the third vertex be (x, y), then
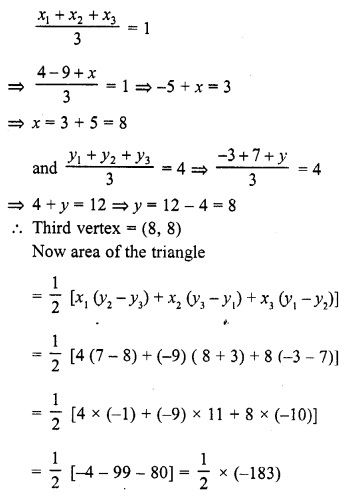
= \(\frac { 183 }{ 2 }\) sq. units
Question 20.
The line segment joining points (-3, -4) and (1, -2) is divided by y-axis in the ratio
(a) 1 : 3
(b) 2 : 3
(c) 3 : 1
(d) 2 : 3
Solution:
(c) The point lies on y-axis
Its abscissa will be zero
Let the point divides the line segment joining the points (-3, -4) and (1, -2) in the ratio m : n
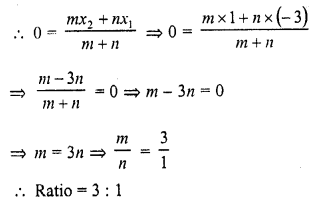
Question 21.
The ratio in which (4, 5) divides the join of (2, 3) and (7, 8) is
(a) -2 : 3
(b) -3 : 2
(c) 3 : 2
(d) 2 : 3
Solution:
(d) Let the point (4, 5) divides the line segment joining the points (2, 3) and (7, 8) in the ratio m : n
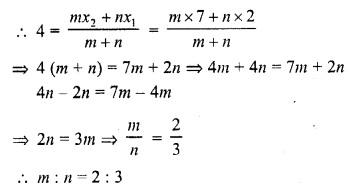
Question 22.
The ratio in which the X-axis divides the segment joining (3, 6) and (12, -3) is
(a) 2 : 1
(b) 1 : 2
(c) -2 : 1
(d) 1 : -2
Solution:
(a) The point lies on x-axis
Its ordinate is zero
Let this point divides the line segment joining the points (3, 6) and (12, -3) in the ratio m : n
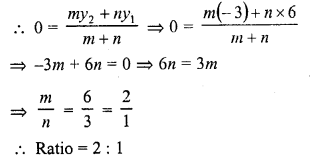
Question 23.
If the centroid of the triangle formed by the points (a, b), (b, c) and (c, a) is at the origin, then a3 + b3 + c3 =
(a) abc
(b) 0
(c) a + b + c
(d) 3 abc
Solution:
(d) Centroid of the triangle formed by the points (a, b), (b, c) and (c, a) is origin (0, 0)
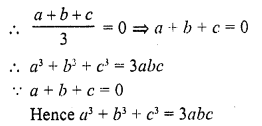
Question 24.
If points (1, 2), (-5, 6) and (a, -2) are collinear, then a =
(a) -3
(b) 7
(c) 2
(d) -2
Solution:
(b) The area of a triangle whose vertices are (1, 2), (-5, 6) and (a, -2)
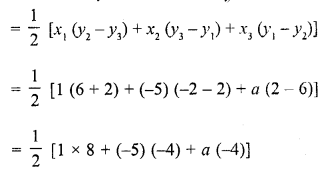
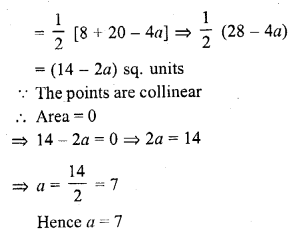
Question 25.
If the centroid of the triangle formed by (7, x), (y, -6) and (9, 10) is at (6, 3), then (x, y) =
(a) (4, 5)
(b) (5, 4)
(c) (-5, -2)
(d) (5, 2)
Solution:
(d) Centroid of (7, x), (y, -6) and (9, 10) is (6, 3)
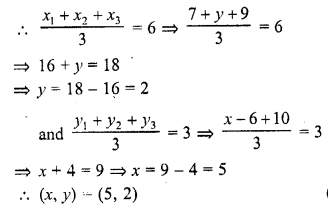
Question 26.
The distance of the point (4, 7) from the x-axis is
(a) 4
(b) 7
(c) 11
(d) √65
Solution:
(b) The distance of the point (4, 7) from x-axis = 7
Question 27.
The distance of the point (4, 7) from the y-axis is
(a) 4
(b) 7
(c) 11
(d) √65
Solution:
(a) The distance of the point (4, 7) from y-axis = 4
Question 28.
If P is a point on x-axis such that its distance from the origin is 3 units, then the coordinates of a point Q on OY such that OP = OQ, are
(a) (0, 3)
(b) (3, 0)
(c) (0, 0)
(d) (0, -3)
Solution:
(a) P is a point on x-axis and its distance from 0 is 3
Co-ordinates of P will be (3, 0)
Q is a point on OY such that OP = OQ
Co-ordinates of Q will be (0, 3)
Question 29.
If the point (x, 4) lies on a circle whose centre is at the origin and radius is 5, then x =
(a) ±5
(b) ±3
(c) 0
(d) ±4
Solution:
(b) Point A (x, 4) is on a circle with centre O (0, 0) and radius = 5
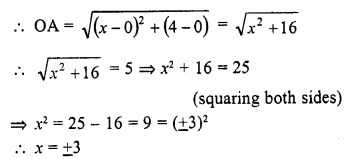
Question 30.
If the point P (x, y) is equidistant from A (5, 1) and B (-1, 5), then
(a) 5x = y
(b) x = 5y
(c) 3x = 2y
(d) 2x = 3y
Solution:
(c)
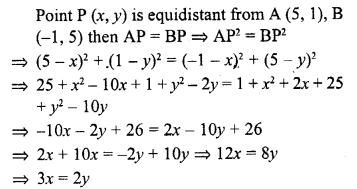
Question 31.
If points A (5, p), B (1, 5), C (2, 1) and D (6, 2) form a square ABCD, then p =
(a) 7
(b) 3
(c) 6
(d) 8
Solution:
(c) Vertices of a square are A (5, p), B (1, 5), C (2, 1) and D (6, 2)
The diagonals bisect each other at O
O is the mid-point of AC and BD
O is mid-point of BD, then
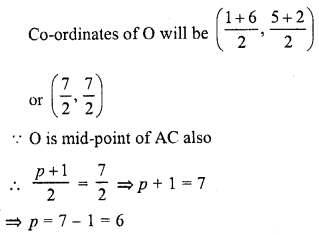
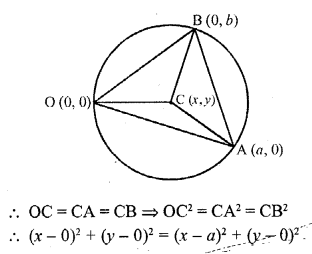
Question 32.
The coordinates of the circumcentre of the triangle formed by the points O (0, 0), A (a, 0) and B (0, b) are
(a) (a, b)
(b) (\(\frac { a }{ 2 }\) , \(\frac { b }{ 2 }\))
(c) (\(\frac { b }{ 2 }\) , \(\frac { a }{ 2 }\))
(d) (b, a)
Solution:
(b) Let co-ordinates of C be (x, y) which is the centre of the circumcircle of ∆OAB
Radii of a circle are equal
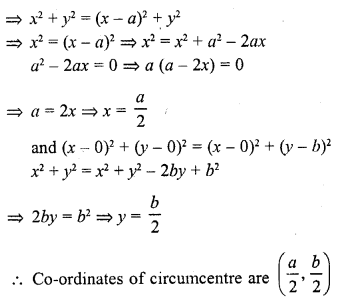
Question 33.
The coordinates of a point on x-axis which lies on the perpendicular bisector of the line segment joining the points (7, 6) and (-3, 4) are
(a) (0, 2)
(b) (3, 0)
(b) (0, 3)
(d) (2, 0)
Solution:
(d) The given point P lies on x-axis
Let the co-ordinates of P be (x, 0)
The point P lies on the perpendicular bisector of of the line segment joining the points A (7, 6), B (-3, 4)

Question 34.
If the centroid of the triangle formed by the points (3, -5), (-7, 4), (10, -k) is at the point (k, -1), then k =
(a) 3
(b) 1
(c) 2
(d) 4
Solution:
(c) O (k, -1) is the centroid of triangle whose vertices are
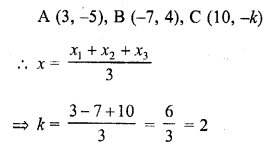
Question 35.
If (-2, 1) is the centroid of the triangle having its vertices at (x, 0), (5, -2), (-8, y), then x, y satisfy the relation
(a) 3x + 8y = 0
(b) 3x – 8y = 0
(c) 8x + 3y = 0
(d) 8x = 3y
Solution:
(-2, 1) is the centroid of triangle whose vertices are (x, 0), (5, -2), (-8, y)
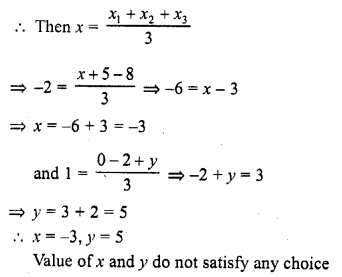
Question 36.
The coordinates of the fourth vertex of the rectangle formed by the points (0, 0), (2, 0), (0, 3) are
(a) (3, 0)
(b) (0, 2)
(c) (-2, 3)
(d) (3, 2)
Solution:
(c) Three vertices of a rectangle are A (0, 0), B (2, 0), C (0, 3)
Let fourth vertex be D (x, y)
The diagonals of a rectangle bisect eachother at O
O is the mid-point of AC, then
Coordinates of O will be (\(\frac { 0+0 }{ 2 }\) , \(\frac { 0+3 }{ 2 }\))
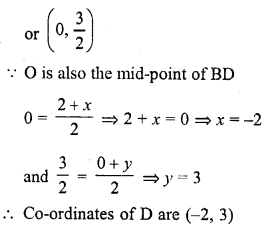
Question 37.
The length of a line segment joining A (2, -3) and B is 10 units. If the abscissa of B is 10 units, then its ordinates can be
(a) 3 or -9
(b) -3 or 9
(c) 6 or 27
(d) -6 or-27
Solution:
(a) Abscissa of B is 10 and co-ordinates of A are (2, -3)
Let ordinates of B be y, then
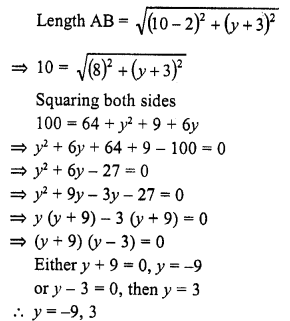
Question 38.
The ratio in which the line segment joining P(x1, y1) and Q (x2, y2) is divided by x-axis is
(a) y1 : y2
(b) -y1 : y2
(c) x1 : x2
(d) -x1 : x2
Solution:
(b) Let a point A on x-axis divides the line segment joining the points P (x1, y1), Q (x2, y2) in the ratio m1 : m2 and
let co-ordinates of A be (x, 0)
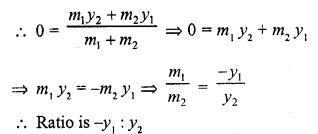
Question 39.
The ratio in which the line segment joining points A (a1, b1) and B (a2, b2) is divided by y-axis is
(a) -a1 : a2
(b) a1 : a2
(c) b1 : b2
(d) -b1 : b2
Solution:
(a) Let the point P on y-axis, divides the line segment joining the point A (a1, b1) and B (a2, b2) is the ratio m1 : m2 and
let the co-ordinates of P be (0, y), then
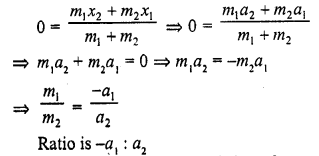
Question 40.
If the line segment joining the points (3, -4) and (1, 2) is trisected at points P
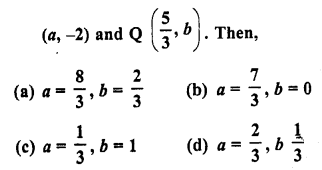
Solution:
(b)
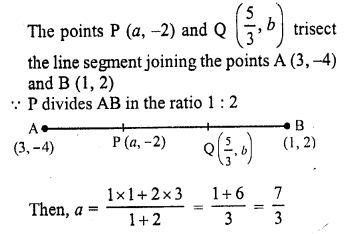
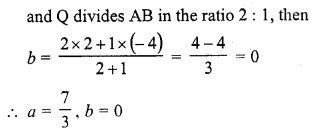
Question 41.
If the coordinates of one end of a diameter of a circle are (2, 3) and the coordinates of its centre are (-2, 5), then the coordinates of the other end of the diameter are [CBSE 2012]
(a) (-6, 7)
(b) (6, -7)
(c) (6, 7)
(d) (-6, -7)
Solution:
(a) Let AB be the diameter of a circle with centre O
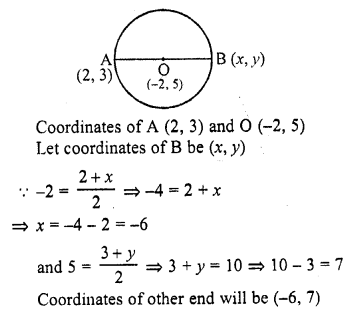
Question 42.
The coordinates of the point P dividing the line segment joining the points A (1, 3) and B (4, 6) in the ratio 2 : 1 are
(a) (2, 4)
(b) (3, 5)
(c) (4, 2)
(d) (5, 3) [CBSE 2012]
Solution:
(b) Point P divides the line segment joining the points A (1, 3) and B (4, 6) in the ratio 2 : 1
Let coordinates of P be (x, y), then
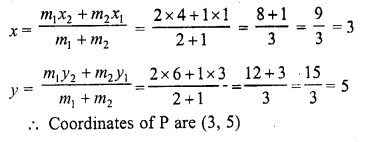
Question 43.
In the figure, the area of ∆ABC (in square units) is [CBSE 2013]
(a) 15
(b) 10
(c) 7.5
(d) 2.5
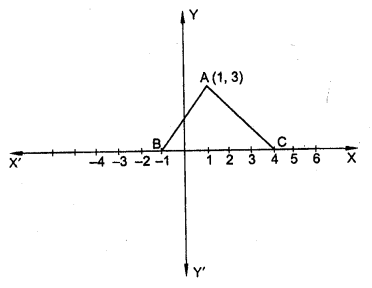
Solution:
(c)
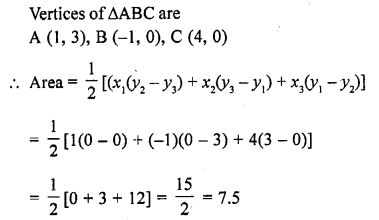
Question 44.
The point on the x-axis which is equidistant from points (-1, 0) and (5, 0) is
(a) (0, 2)
(b) (2, 0)
(c) (3, 0)
(d) (0, 3) [CBSE 2013]
Solution:
(c) Let the point P (x, 0) is equidistant from the points A (-1, 0), B (5, 0)
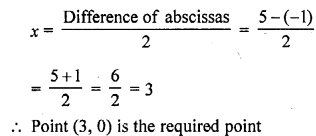
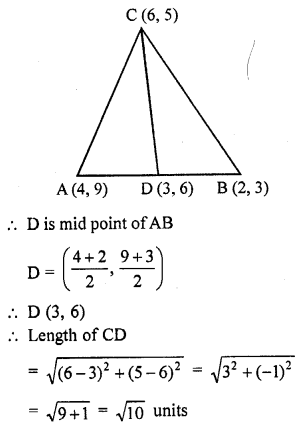
Question 45.
If A (4, 9), B (2, 3) and C (6, 5) are the vertices of ∆ABC, then the length of median through C is
(a) 5 untis
(b) √10 units
(c) 25 units
(d) 10 units [CBSE 2014]
Solution:
(b) A (4, 9), B (2, 3) and C (6, 5) are the vertices of ∆ABC
Let median CD has been drawn C (6, 5)
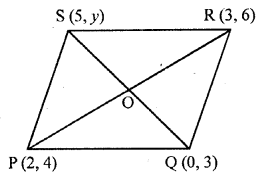
Question 46.
If P (2, 4), Q (0, 3), R (3, 6) and S (5, y) are the vertices of a paralelogram PQRS, then the value of y is
(a) 7
(b) 5
(c) -7
(d) -8 [CBSE 2014]
Solution:
(a) P (2, 4), Q (0, 3), R (3, 6) and S (5, y) are the vertices of a ||gm PQRS

Question 47.
If A (x, 2), B (-3, -4) and C (7, -5) are collinear, then the value of x is
(a) -63
(b) 63
(c) 60
(d) -60 [CBSE 2014]
Solution:
(a) A (x, 2), B (-3, -4) and C (7, -5) are collinear, then area ∆ABC = 0
Now area of ∆ABC
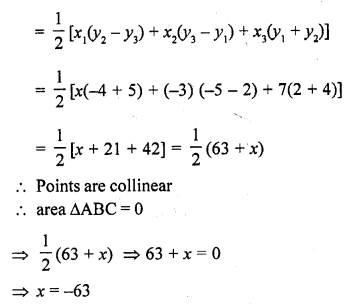
Question 48.
The perimeter of a triangle with vertices (0, 4) and (0, 0) and (3, 0) is
(a) 7 + √5
(b) 5
(c) 10
(d) 12 [CBSE 2014]
Solution:
(d) A (0, 4) and B (0, 0) and C (3, 0) are the vertices of ∆ABC

Question 49.
If the point P (2, 1) lies on the line segment joining points A (4, 2) and B (8, 4), then
(a) AP = \(\frac { 1 }{ 3 }\) AB
(b) AP = BP
(c) BP = \(\frac { 1 }{ 3 }\) AB
(d) AP = \(\frac { 1 }{ 2 }\) AB
Solution:
(d) Given that, the point P (2, 1) lies on the line segment joining the points (4, 2) and B (8, 4), which shows in the figure below:


Question 50.
A line intersects the y-axis and x-axis at P and Q, respectively. If (2, -5) is the mid-point of PQ, then the coordinates of P and Q are, respectively
(a) (0, -5) and (2, 0)
(b) (0, 10) and (-4, 0)
(c) (0, 4) and (-10, 0)
(d) (0, -10) and (4, 0)
Solution:
(d) Let the coordinates of P and Q (0, y) and (x, 0), respectively.
So, the mid-point of P (0, y) and Q (x, 0) is
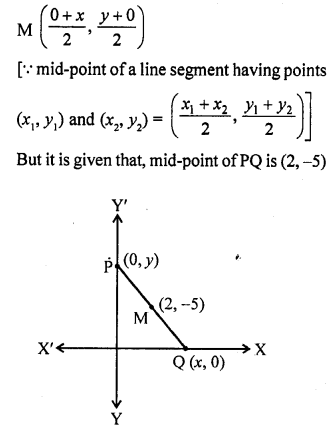
2 = \(\frac { x + 0 }{ 2 }\) and -5 = \(\frac { y + 0 }{ 2 }\)
=> 4 = x and -10 = y
=> x = 4 and y = -10
So, the coordinates of P and Q are (0, -10) and (4, 0).
Hope given RD Sharma Class 10 Solutions Chapter 6 Co-ordinate Geometry MCQS are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.