RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.6
These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.6. You must go through NCERT Solutions for Class 10 Maths to get better score in CBSE Board exams along with RS Aggarwal Class 10 Solutions.
Other Exercises
- RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.1
- RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.2
- RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3
- RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.4
- RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.5
- RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.6
- RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.7
- RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8
- RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9
- RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10
- RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11
- RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12
- RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13
- RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS
- RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS
Question 1.
Determine the nature of the roots of following quadratic equations :
(i) 2x² – 3x + 5 = 0 [NCERT]
(ii) 2x² – 6x + 3 = 0 [NCERT]
(iii) \(\frac { 3 }{ 5 }\) x² – \(\frac { 2 }{ 3 }\) x + 1 = 0
(iv) 3x² – 4√3 x + 4 = 0 [NCERT]
(v) 3x² – 2√6 x + 2 = 0
Solution:
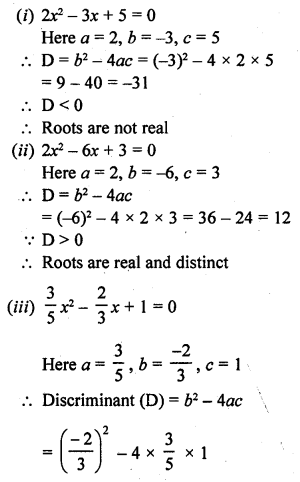

Question 2.
Find the values of k for which the roots are real and equal in each of the following equations :
(i) kx² + 4x + 1 = 0
(ii) kx² – 2√5 x + 4 = 0
(iii) 3x² – 5x + 2k = 0
(iv) 4x²+ kx + 9 = 0
(v) 2kx² – 40x + 25 = 0
(vi) 9x² – 24x + k = 0
(vii) 4x² – 3kx +1 = 0
(viii) x² – 2 (5 + 2k) x + 3 (7 + 10k) = 0
(ix) (3k + 1) x² + 2(k + 1) x + k = 0
(x) kx² + kx + 1 = – 4x² – x
(xi) (k + 1) x² + 2 (k + 3) x + (k + 8) = 0
(xii) x² – 2kx + 7k – 12 = 0
(xiii) (k + 1) x² – 2 (3k + 1) x + 8k + 1 = 0
(xiv) 5x² – 4x + 2 + k (4x² – 2x – 1) = 0
(xv) (4 – k) x² + (2k + 4) x (8k + 1) = 0
(xvi) (2k + 1) x² + 2 (k + 3) x (k + 5) = 0
(xvii) 4x² – 2 (k + 1) x + (k + 4) = 0
(xviii) 4x² (k + 1) x + (k + 1) = 0
Solution:
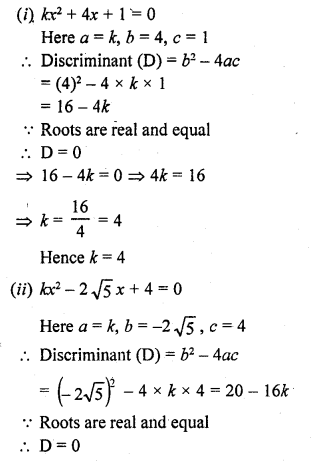
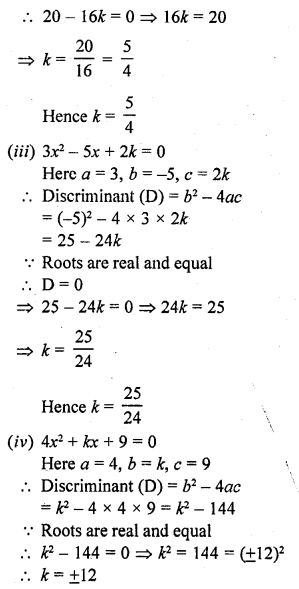

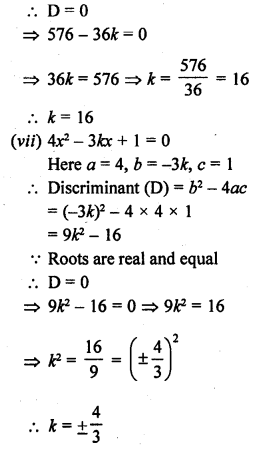
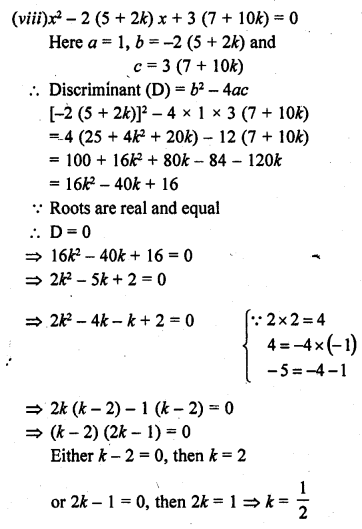

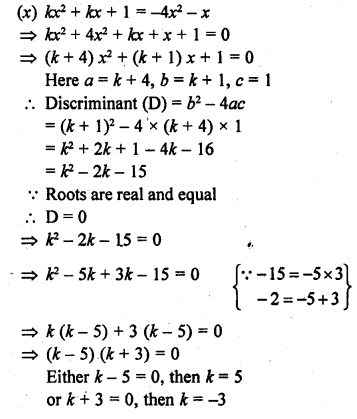
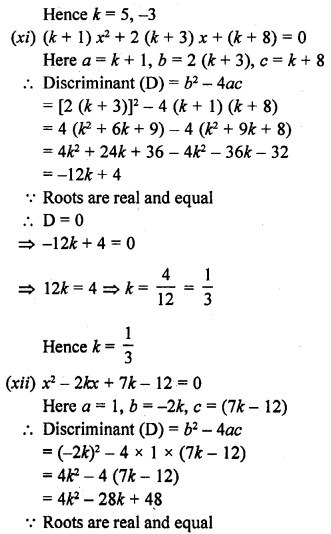
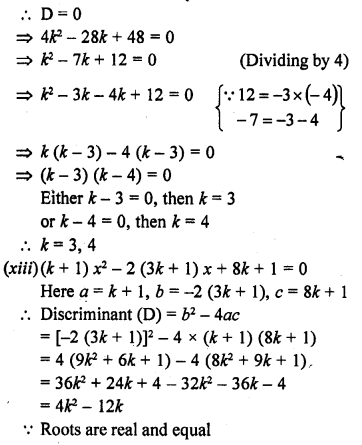
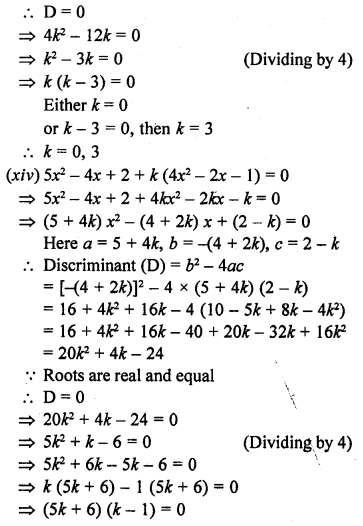
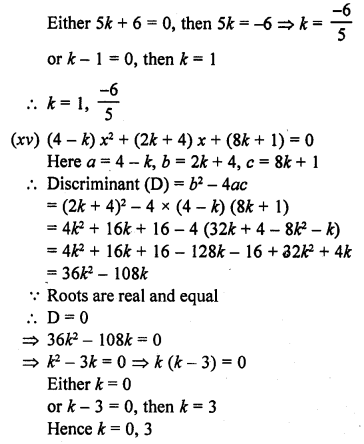
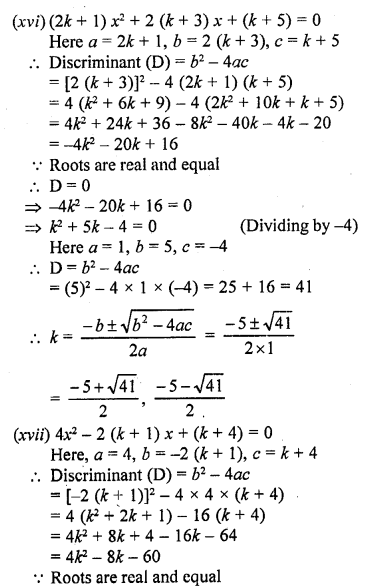
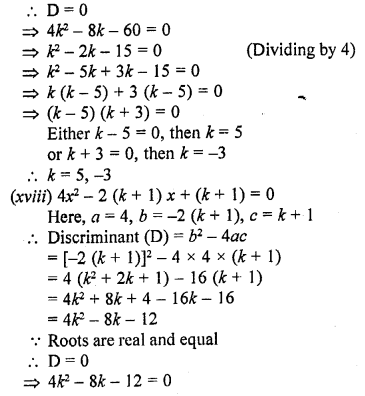
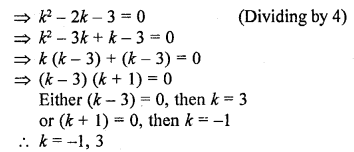
Question 3.
In the following, determine the set of values of k for which the given quadratic equation has real roots :
(i) 2x² + 3x + k = 0
(ii) 2x² + x + k = 0
(iii) 2x² – 5x – k = 0
(iv) kx² + 6x + 1 = 0
(v) 3x² + 2x + k = 0
Solution:



Question 4.
Find the values of k for which the following equations have real and equal roots :
(i) x²- 2(k + 1) x + k² = 0 [CBSE 2001C, 2013]
(ii) k²x² – 2 (2k – 1) x + 4 = 0 [CBSE 2001C]
(iii) (k + 1) x² – 2(k – 1) x + 1 = 0 [CBSE 2002C]
(iv) x² + k(2x + k – 1) + 2 = 0 [CBSE 2017]
Solution:
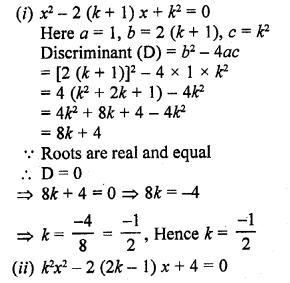
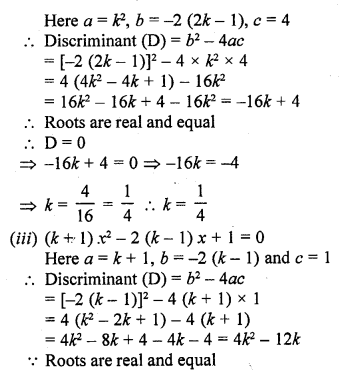
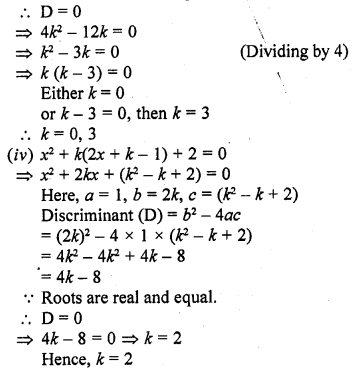
Question 5.
Find the values of k for which the following equations have real roots
(i) 2x² + kx + 3 = 0 [NCERT]
(ii) kx (x – 2) + 6 = 0 [NCERT]
(iii) x² – 4kx + k = 0 [CBSE 2012]
(iv) kx(x – 2√5 ) + 10 = 0 [CBSE 2013]
(v) kx (x – 3) + 9 = 0 [CBSE 2014]
(vi) 4x² + kx + 3 = 0 [CBSE 2014]
Solution:
(i) 2x² + kx + 3 = 0
Here a = 2, b = k, c = 3
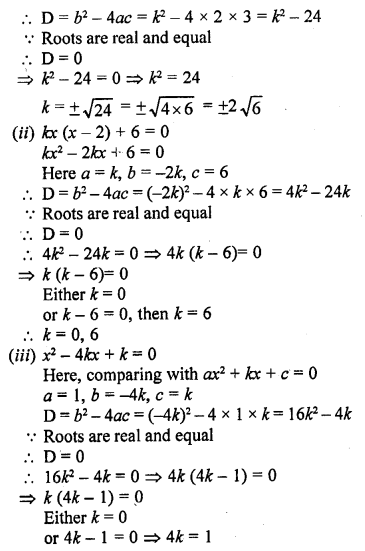
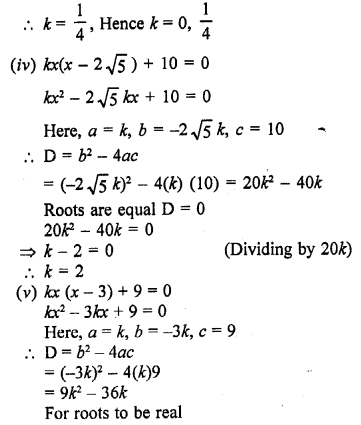
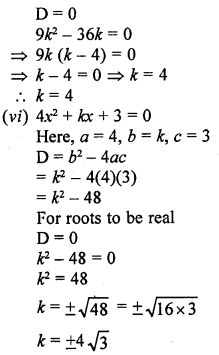
Question 6.
Find the values of k for which the given quadratic equation has real and distinct roots :
(i) kx² + 2x + 1 = 0
(ii) kx² + 6x + 1 = 0
Solution:

Question 7.
For what value of k, (4 – k) x² + (2k + 4) x + (8k + 1) = 0, is a perfect square.
Solution:
(4 – k) x² + (2k + 4) x + (8k + 1) = 0
Here, a = 4 – k, b = 2k + 4, c = 8k + 1

Question 8.
Find the least positive value of k for which the equation x² + kx + 4 = 0 has real roots.
Solution:
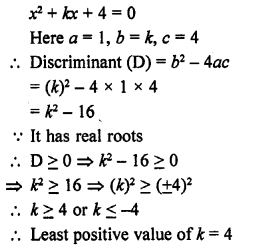
Question 9.
Find the value of k for which the quadratic equation (3k + 1) x² + 2(k + 1) x + 1 = 0 has equal roots. Also, find the roots.
[CBSE 2014]
Solution:
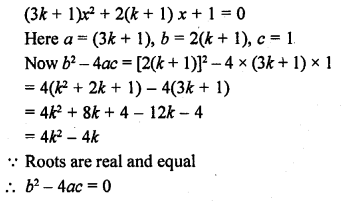
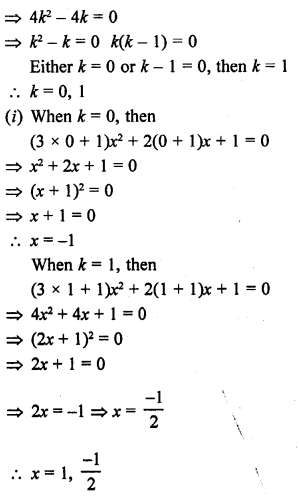
Question 10.
Find the values of p for which the quadratic equation (2p + 1) x² – (7p + 2) x + (7p – 3) = 0 has equal roots. Also, find these roots.
Solution:
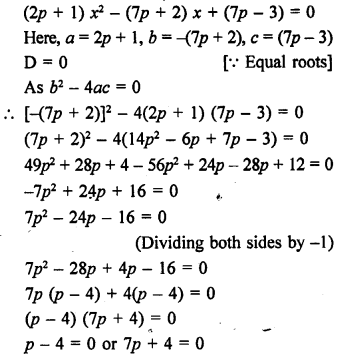
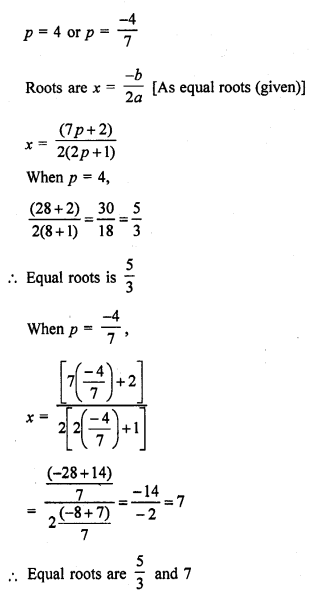
Question 11.
If – 5 is a root of the quadratic equation 2x² + px – 15 = 0 and the quadratic equation p(x² + x) + k = 0 has equal-roots, find the value of k. [CBSE 2014]
Solution:
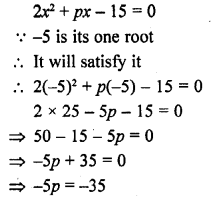
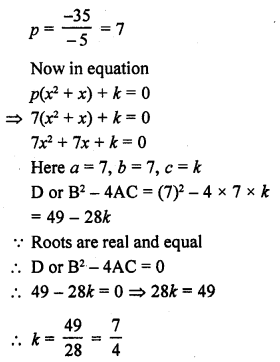
Question 12.
If 2 is a root of the quadratic equation 3x² + px – 8 = 0 and the quadratic equation 4x² – 2px + k = 0 has equal roots, find the value of k. [CBSE 2014]
Solution:
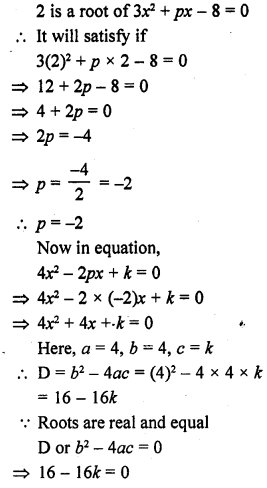
=> 16k = 16
k = 16
Question 13.
If 1 is a root of the quadratic equation 3x² + ax – 2 = 0 and the quadratic equation a(x² + 6x) – b=0 has equal roots, find the value of b.
Solution:
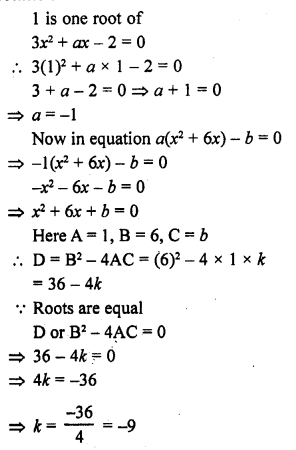
Question 14.
Find the value of p for which the quadratic equation (p + 1) x² – 6 (p + 1) x + 3 (p + q) = 0, p ≠ -1 has equal roots. Hence, find the roots of the equation. [CBSE 2015]
Solution:
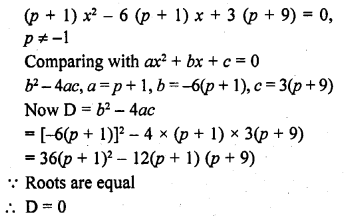
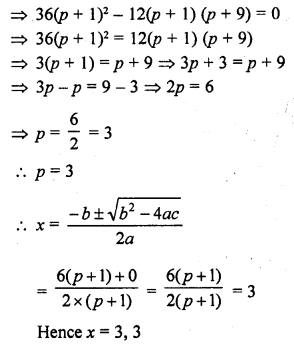
Question 15.
Determine the nature of the roots of following quadratic equations :
(i) (x – 2a) (x – 2b) = 4ab
(ii) 9a²b²x² – 24abcdx + 16c²d² = 0, a ≠ 0, b ≠ 0
(iii) 2 (a² + b²) x² + 2 (a + b) x + 1 = 0
(iv) (b + c) x² – (a + b + c) x + a = 0
Solution:

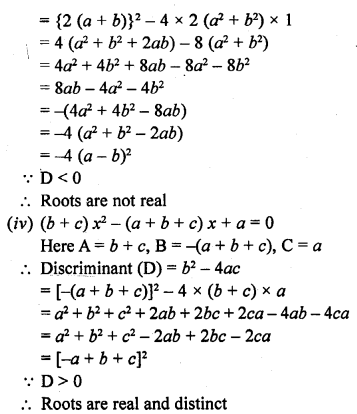
Question 16.
Determine the set of values of k for which the given following quadratic equation has real roots :
(i) x² – kx + 9 = 0
(ii) 2x² + kx + 2 = 0
(iii) 4x² – 3kx +1=0
(iv) 2x² + kx – 4 = 0
Solution:
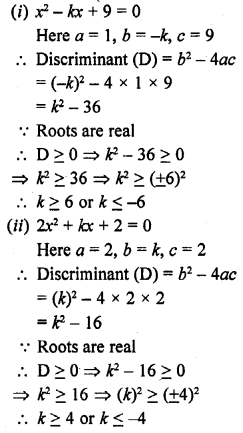
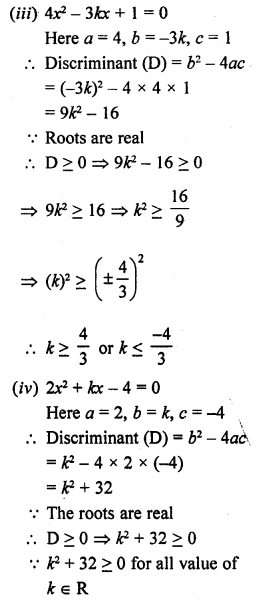
Question 17.
If the roots of the equation (b – c) x² + (c – a) x + (a – b) = 0 are equal, then prove that 2b = a + c. [CBSE 2002C]
Solution:
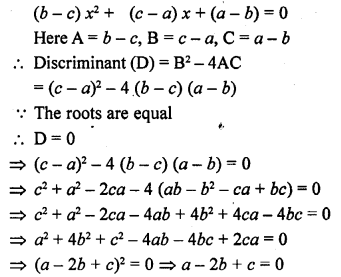
=> a + c = 2b
=> 2b = a + c
Hence proved.
Question 18.
If the roots of the equation (a² + b²) x² – 2 (ac + bd) x + (c² + d²) = 0 are equal. prove that \(\frac { a }{ b }\) = \(\frac { c }{ d }\)
Solution:

Question 19.
If the roots of the equations ax² + 2bx + c = 0 and bx² – 2√ac x + b = 0 are simultaneously real, then prove that b² = ac
Solution:
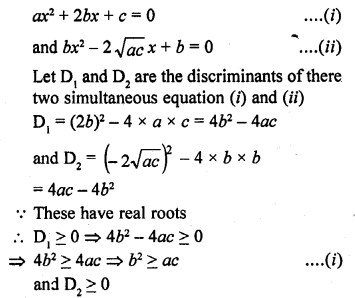
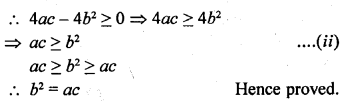
Question 20.
If p, q are real and p ≠ q, then show that the roots of the equation (p – q) x² + 5(p + q) x – 2(p – q) = 0 are real and unequal.
Solution:
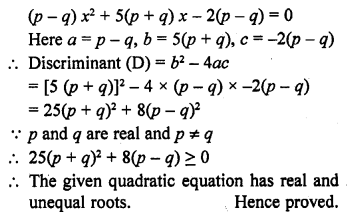
Question 21.
If the roots of the equation (c² – ab) x² – 2 (a² – bc) x + b² – ac = 0 are equal, prove that either a = 0 or a3 + b3 + c3 = 3abc.
Solution:
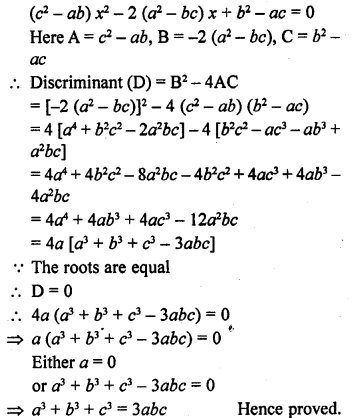
Question 22.
Show that the equation 2 (a² + b²) x² + 2 (a + b) x + 1 = 0 has no real roots, when a ≠ b.
Solution:

Question 23.
Prove that both the roots of the equation (x – a) (x – b) + (x – b) (x – c) + (x – c) (x – a) = 0 are real but they are equal only when a = b = c.
Solution:

Question 24.
If a, b, c are real numbers such that ac ≠ 0, then show that at least one of the equations ax² + bx + c = 0 and – ax² + bx + c = 0 has real roots.
Solution:

Question 25.
If the equation (1 + m²) x² + 2mcx + (c² – a²) = 0 has equal roots, prove that c² = a² (1 + m²). (C.B.S.E. 1999)
Solution:
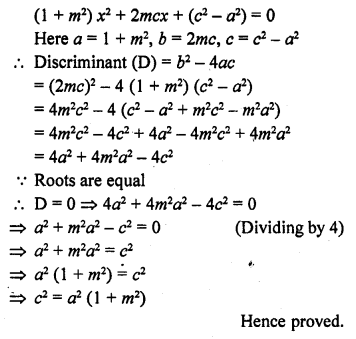
Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.6 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.