RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1
These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1
Other Exercises
- RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1
- RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.2
- RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.3
- RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.4
- RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.5
- RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.6
- RD Sharma Class 10 Solutions Chapter 15 Statistics Ex VSAQS
- RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS
Question 1.
Calculate the mean for the following distribution :
| X | 5 | 6 | 7 | 8 | 9 |
| f | 4 | 8 | 14 | 11 | 3 |
Solution:
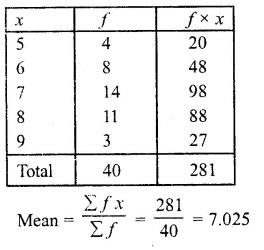
Question 2.
Find the mean of the following data:
| X | 19 | 21 | 23 | 25 | 27 | 29 | 31 |
| f | 13 | 15 | 16 | 18 | 16 | 15 | 13 |
Solution:
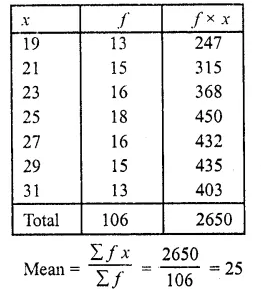
Question 3.
If the mean of the following data is 20.6. Find the value of p. (C.B.S.E. 1997)
| X | 10 | 15 | p | 25 | 35 |
| y | 3 | 10 | 25 | 7 | 5 |
Solution:

Question 4.
If the mean of the following data is 15, find p. (C.B.S.E. 1992C)
| X | 5 | 10 | 15 | 20 | 25 |
| f | 6 | P | 6 | 10 | 5 |
Solution:

Question 5.
Find the value of p for the following distribution whose mean is 16.6.
| X | 8 | 12 | 15 | P | 20 | 25 | 30 |
| f | 12 | 16 | 20 | 24 | 16 | 8 | 4 |
Solution:
Mean = 16.6

Question 6.
Find the missing value of p for the following distribution whose mean is 12.58. (C.B.S.E. 1992C)
| X | 5 | 8 | 10 | 12 | P | 20 | 25 |
| f | 2 | 5 | 8 | 22 | 7 | 4 | 2 |
Solution:

Question 7.
Find the missing frequency (p) for the following distribution whose mean is 7.68.
| X | 3 | 5 | 7 | 9 | 11 | 13 |
| f | 6 | 8 | 15 | P | 8 | 4 |
Solution:

Question 8.
The following table gives the number of boys of a particular age in a class of 40 students. Calculate the mean age of the students
| Age (in years) | 15 | 16 | 17 | 18 | 19 | 20 |
| No. of students | 3 | 8 | 10 | 10 | 5 | 4 |
Solution:
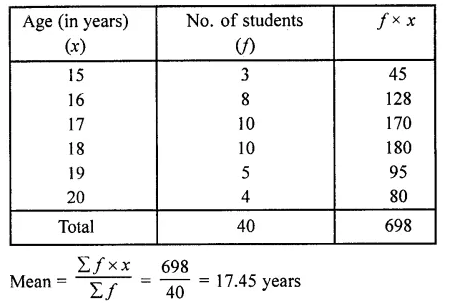
Question 9.
Candidates of four schools appear in a mathematics test. The data were as follows :
| Schools | No. of Candidates | Average Score |
| I | 60 | 75 |
| II | 48 | 80 |
| III | Not available | 55 |
| IV | 40 | 50 |
If the average score of the candidates of all the four schools is 66, find the number of candidates that appeared from school III.
Solution:

Question 10.
Five coins were simultaneously tossed 1000 times and at each toss the number of heads were observed. The number of tosses during which 0, 1, 2, 3, 4 and 5 heads were obtained are shown in the table below. Find the mean number of heads per toss.
| No. of heads per toss | No. of tosses |
| 0 | 38 |
| 1 | 144 |
| 2 | 342 |
| 3 | 287 |
| 4 | 164 |
| 5 | 25 |
| Total | 1000 |
Solution:
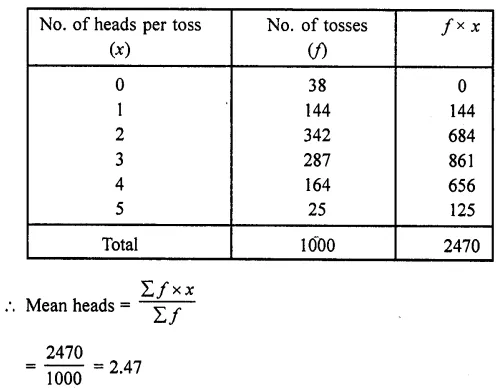
Question 11.
The arithmetic mean of the following data is 14, find the value of k. (C.B.S.E. 2002C)
| X | 5 | 10 | 15 | 20 | 25 |
| f | 7 | k | 8 | 4 | 5 |
Solution:
Mean=14
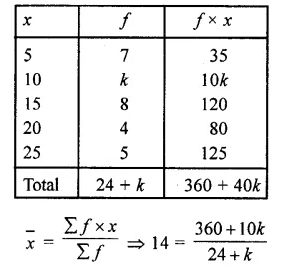
⇒ 14 (24 + k) = 360 + 10k
⇒ 336 + 14k = 360 + 10k
⇒ 14k- 10k- 360 -336 24
⇒ 4k = 24
⇒ k= \(\frac { 24 }{ 4 }\) = 6 4
Hence k = 6
Question 12.
The arithmetic mean of the following data is 25, find the value of k. (C.B.S.E. 2001)
| X | 5 | 15 | 25 | 35 | 45 |
| f | 3 | k | 3 | 6 | 2 |
Solution:
Mean =25
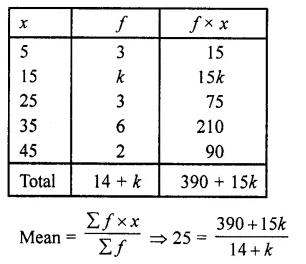
⇒ 25 (14 + k) = 390 + 15k
⇒ 350 + 25k= 390 + 15k
⇒ 25k- 15k = 390 -350
⇒ 10k = 40 ⇒ k = \(\frac { 40 }{ 10 }\) = 4
Hence k = 4
Question 13.
If the mean of the following data is 18.75. Find the value of p.
|
X |
10 | 15 | P | 25 | 30 |
| f | 5 | 10 | 7 | 8 | 2 |
Solution:
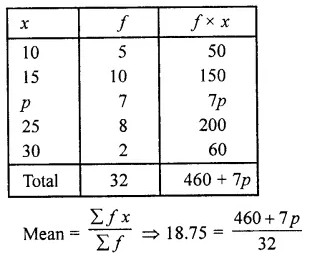
⇒ 460 + 7p = 32 (18.75)
⇒ 460 + 7p = 600
⇒ 7p = 600 – 460 = 140
⇒ p = \(\frac { 140 }{ 7 }\) = 20
∴ p = 20
Question 14.
Find the value of p, if the mean of the following distribution is 20.
| X | 15 | 17 | 19 | 20 + p | 23 |
| f | 2 | 3 | 4 | 5p | 6 |
Solution:

⇒ 5p2 + 100p + 295 = 20 (15 + 5p)
⇒ 5p2 + 100p + 295 = 300 + 100p
⇒ 5p2 + 100p – 100p = 300 – 295
⇒ 5p2 = 5 ⇒ p2 = \(\frac { 5 }{ 5 }\) = 1
⇒ P= ±1
P = -1 i s not possible
∴ p= 1
Question 15.
Find the missing frequencies in the following frequency distribution if it is known that the mean of the distribution is 50.

Solution:

Hope given RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.