Polynomials Class 9 Extra Questions Maths Chapter 2 with Solutions Answers

Here we are providing Polynomials Class 9 Extra Questions Maths Chapter 2 with Answers Solutions, Extra Questions for Class 9 Maths was designed by subject expert teachers.

Extra Questions for Class 9 Maths Polynomials with Answers Solutions

Extra Questions for Class 9 Maths Chapter 2 Polynomials with Solutions Answers

Polynomials Class 9 Extra Questions Very Short Answer Type

Question 1.
Factorise : 125x³ – 64y³
Solution:
125x³– 6443 = (5x)³ – (4y)³
By using a3 – b3 = (a – b) (a² + ab + b²), we obtain
125x³– 64y³ = (5x – 4y) (25x² + 20xy + 16y²)

Question 2.
Find the value of (x + y)² + (x – y)².
Solution:
(x + y)² + (x – y)² = x² + y² + 2xy + x² + y² – 2xy
= 2x² + 2y² = 21x² + y²)

Question 3.
If p(x)= x² – 2√2x+1, then find the value of p(2√2)
Solution:
Put x = 2√2 in p(x), we obtain
p(2√2) = (2√2)² – 2√2(2√2) + 1 = (2√2)² – (2√2)² + 1 = 1

Question 4.
Find the value of m, if x + 4 is a factor of the polynomial x² + 3x + m.
Solution:
Let p(x) = x² + 3x + m
Since (x + 4) or (x – (-4)} is a factor of p(x).
∴ p(-4) = 0
⇒ (-4)² + 3(-4) + m = 0
⇒ 16 – 12 + m = 0
⇒ m = -4

Question 5.
Find the remainder when x³+ x² + x + 1 is divided by x – \(\frac{1}{2}\) using remainder theorem.
Solution:
Let p(x) = x³+ x² + x + 1 and q(x) = x – \(\frac{1}{2}\)
Here, p(x) is divided by q(x)
∴ By using remainder theorem, we have

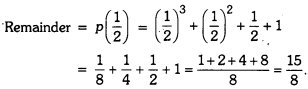
Question 6.
Find the common factor in the quadratic polynomials x² + 8x + 15 and x² + 3x – 10.
Solution:
x² + 8x + 15 = x² + 5x + 3x + 15 = (x + 3) (x + 5)
x² + 3x – 10 = x² + 5x – 2x – 10 = (x – 2) (x + 5)
Clearly, the common factor is x + 5.

Polynomials Class 9 Extra Questions Short Answer Type 1

Question 1.
Expand :
(i) (y – √3)²
(ii) (x – 2y – 3z)²
Solution: (i)
(y – √3)² = y² -2 × y × √3 + (√3)² = y² – 2√3 y + 3 (x – 2y – 3z)²
= x² + 1 – 2y)² + (-3z)² + 2 × x × (-2y) + 2 × (-2y) × (-3z) + 2 × (-3z) × x
= x² + 4y² + 9z² – 4xy + 12yz – 6zx

Question 2.
If x + = \(\frac{1}{x}\) = 7, then find the value of x³ + \(\frac{1}{x^{3}}\)
Solution:
We have x + \(\frac{1}{x}\) = 7
Cubing both sides, we have

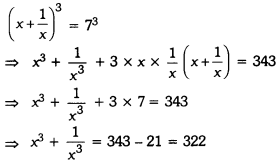
Question 3.
Show that p – 1 is a factor of p¹⁰ + p⁸ + p⁶ – p⁴ – p² – 1.
Solution:
Let f(p) = p¹⁰ + p⁸ + p⁶ – p⁴ – p² – 1
Put p = 1, we obtain
f(1) = 1¹⁰ + 1⁸ + 1⁶ – 1⁴ – 1² – 1
= 1 + 1 + 1 – 1 – 1 – 1 = 0
Hence, p – 1 is a factor of p¹⁰ + p⁸ + p⁶ – p⁴ – p² – 1.

Question 4.
If 3x + 2y = 12 and xy = 6, find the value of 27x³ + 8y³
Solution:
We have 3x + 2y = 12
On cubing both sides, we have
⇒ (3x + 2y)³ = 12³
⇒ (3x)³ +(2y)³ + 3 × 3x × 2y(3x + 2y) = √728
⇒ 27x³+ 8y³ + 18xy(3x + 2y) = √728
⇒ 27x³+ 8y³ + 18 × 6 × 12 = √728
⇒ 27x³+ 8y³ + 1296 = √728
⇒ 27x³+ 8y³ = √728 – 1296
⇒ 27x³+ 8y³ = 432

Question 5.
Factorise : 4x² + 9y² + 16z²2 + 12xy – 24 yz – 16xz.
Solution:
4x² + 9y² + 16z²2 + 12xy – 24yz – 16xz
= (2x)² + (3y)² + (-4z)² + 2(2x)(3y) + 2(3y)(= 42) + 2(- 42)(2x)
By using a² + b² + 2ab + 2bc + 2ca = (a + b + c)², we obtain
= (2x + 3y – 4z)² = (2x + 3y – 4z) (2x + 3y – 4z)

Question 6.
Factorise : 1 – 2ab – (a² + b²).
Solution:
1 – 2ab – (a² + b²) = 1 – (a² + b² + 2ab)
= 1² – (a + b)²
= (1 + a + b) (1 – a – b) [∵ x² – y² = (x + y)(x – y)]

Polynomials Class 9 Extra Questions Short Answer Type 2

Question 1.
Factorise :

Solution:

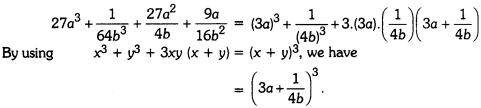
Question 2.
Factorise 64a³ – 27b³ – 144a²b + 108ab².
Solution:
64a² – 27b² – 144a²b + 108ab²
= (4a)³ – (3b)³ – 36ab(4a – 3b)
= (40)² – (3b)³ – 3 × 4a × 3b (4a – 3b)
= (4a – 3b)³ [∵ (x – y)³ = x³ – y³ – 3xy(x – y)]
= (40 – 3b) (4a – 3b) (4a – 3b)

Question 3.
What are the possible expressions for the dimensions of a cuboid whose volume is given below ?
Volume = 12ky² + 8ky – 20k.
Solution:
We have, volume = 12ky² + 8ky – 20k
= 4k(3y² + 2y – 5) = 4k(3y² + 5y – 3y – 5)
= 4k[y(3y + 5) – 1(3y + 5)] = 4k(3y + 5) (y – 1)
∴Possible expressions for the dimensions of cuboid are 4k units, (3y + 5) units and (y – 1) units.

Question 4.
If p(x) = x³ + 3x² – 2x + 4, then find the value of p(2) + p(-2) – P(0).
Solution:
Here, p(x) = x³+ 3x² – 2x + 4
Now, p(2) = 2³ + 3(2)² – 2(2) + 4
= 8 + 12 – 4 + 4 = 20
p(-2) = (-2)³ + 3(-2)² – 21 – 2) + 4
= 8 + 12 + 4 + 4 = 12
and p(0) = 0 + 0 – 0 + 4 = 4
∴ p(2) + p(-2) – p(0) = 20 + 12 – 4 = 28.

Question 5.
If one zero of the polynomial x² – √3x + 40 is 5, which is the other zero ?
Solution:
Let p(x) = x² – √3x + 40
= x² – 5x – 8x + 40 = x(x – 5) – 8(x – 5) = (x – 5) (x – 8)
Now, for zeroes of given polynomial, put p(x) = 0
∴ (x – 5) (x – 8) = 0
⇒ x = 5 or x = 8
Hence, other zero is 8.

Question 6.
Simplify:

Solution:

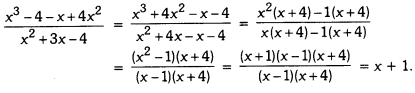
Question 7.
If one zero of the polynomial x² – √3x + 40 is 5, which is the other zero ?
Solution:
Let
p(x) = x² – √3x + 40
= x² – 5x – 8x + 40 = x(x – 5) – 8(x – 5) = (x – 5) (x – 8)
Now, for zeroes of given polynomial, put p(x) = 0
∴ (x – 5) (x – 8) = 0
x = 5 or x = 8
⇒ Hence, other zero is 8.

Polynomials Class 9 Extra Questions Long Answer Type

Question 1.
Prove that (a + b + c)³ – a³ – b³ – c³ = 3(a + b) (b + c) (c + a).
Solution:
L.H.S. = (a + b + c)³ – a³ – b³ – c³
= {(a + b + c)³ – 3} – {b³ + c³}
= (a + b + c – a) {(a + b + c)² + a² + a(a + b + c)} – (b + c) (b² + c² – bc)
= (b + c) {a² + b² + 2 + 2ab + 2bc + 2ca + a² + a² + ab + ac – b² – a² + bc)
= (b + c) (3a² + 3ab + 3bc + 3ca}
= 3(b + c) {a² + ab + bc + ca}
= 31b + c) {{a² + ca) + (ab + bc)}
= 3(b + c) {a(a + c) + b(a + c)}
= 3(b + c)(a + c) (a + b)
= 3(a + b)(b + c) (c + a) = R.H.S.

Question 2.
Factorise : (m + 2n)² x² – 22x (m + 2n) + 72.
Solution:
Let m + 2n = a
∴ (m + 2n)² x² – 22x (m + 2n) + 72 = a²x² – 22ax + 72
= a²x² – 18ax – 4ax + 72
= ax(ax – 18) – 4(ax – 18)
= (ax – 4) (ax – 18)
= {(m + 2n)x – 4)} {(m + 2n)x – 18)}
= (mx + 2nx – 4) (mx + 2nx – 18).

Question 3.
If x – 3 is a factor of x² – 6x + 12, then find the value of k. Also, find the other factor of the – polynomial for this value of k.
Solution:
Here, x – 3 is a factor of x² – kx + 12
∴ By factor theorem, putting x = 3, we have remainder 0.
⇒ (3)² – k(3) + 12 = 0
⇒ 9 – 3k + 12 = 0
⇒ 3k = 21
⇒ k = 7
Now, x² – 7x + 12 = x² – 3x – 4x + 12
= x(x – 3) – 4(x – 3)
= (x – 3) (x – 4)
Hence, the value of k is 7 and other factor is x – 4.

Question 4.
Find a and b so that the polynomial x³– 10x² + ax + b is exactly divisible by the polynomials (x – 1) and (x – 2).
Solution:
Let p(x) = x³– 10x² + ax + b
Since p(x) is exactly divisible by the polynomials (x – 1) and (x – 2).
∴ By putting x = 1, we obtain
(1)³ – 10(1)² + a(1) + b = 0
⇒ a + b = 9
And by putting x = 2, we obtain
(2)³ – 10(2)² + a(2) + b = 0
8 – 40 + 2a + b = 0
⇒ 2a + b = 32
Subtracting (i) from (ii), we have
a = 23
From (i), we have 23 + b = 9 = b = -14
Hence, the values of a and b are a = 23 and b = -14

Question 5.
Factorise : x² – 6x² + 11x – 6.
Solution:
Let p(x) = x² – 6x² + 11x – 6
Here, constant term of p(x) is -6 and factors of -6 are ± 1, ± 2, ± 3 and ± 6
By putting x = 1, we have
p(1) = (1)³ – 6(1)² + 11(1) – 6 = 1 – 6 + 11 -6 = 0
∴ (x – 1) is a factor of p(x)
By putting x = 2, we have
p(2) = (2)³ – 6(2)² + 11(2) – 6 = 8 – 24 + 22 – 6 = 0
∴ (x – 2) is a factor of p(x)
By putting x = 3, we have
p(3) = (3)³ – 6(3)² + 11(3) – 6 = 27 – 54 + 33 – 6 = 0
∴ (x – 3) is a factor of p(x) Since p(x) is a polynomial of degree 3, so it cannot have more than three linear factors.
∴ x³ – 6x² + 11x – 6 = k (x – 1) (x – 2) (x – 3)
By putting x = 0, we obtain
0 – 0 + 0 – 6 = k (-1) (-2) (3)
-6 = -6k
k = 1
Hence, x³ – 6x² + 11x – 6 = (x – 1) (x – 2)(x – 3).

Question 6.
Show that \(\frac{1}{3}\)and \(\frac{4}{3}\) are zeroes of the polynomial 9x³ – 6x² – 11x + 4. Also, find the third zero of the polynomial.
Solution:
Let p(x) = 9x³– 6x² – 11x + 4
Put x = \(\frac{1}{3}\), we have

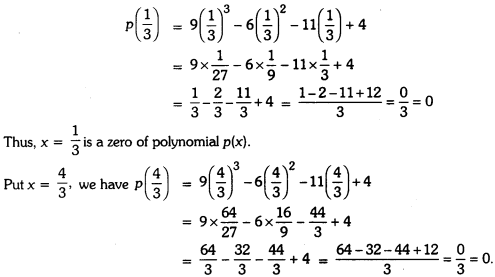
Thus, x = \(\frac{4}{3}\) is another zero of the polynomial p(x). Since x = \(\frac{1}{3}\) and x = \(\frac{4}{3}\) are the zeroes of p(x), therefore, \(\left(x-\frac{1}{3}\right)\) \(\left(x-\frac{4}{3}\right)\) (3x – 1) (3x – 4) or 9x² – 15x + 4 exactly divides p(x).
⇒ 9x³ – 6x² – 11x + 4 = (9x² – 15x + 4) (x + 1)
Hence, x = -1 is its third zero.

Question 7.
Factorise : 6x² – 5x² – √3x + 12
Solution:
Let p(x) = 6x³– 5x² – √3x + 12
Here, constant term of p(x) is 12 and factors of 12 are ± 1, ± 2, ± 3, ± 4, ± 6, ± 12.
By putting x = 1, we have
p(1) = 6(1)³ – 5(1)² – √3(1) + 12 = 6 – 5 – √3 + 12 = 0
∴ (x – 1) is a factor of p(x).
Now, by long division, we have

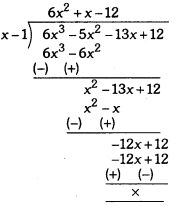
Thus,
p(x) = (x – 1) (6x² + x – 12)
p(x) = (x – 1) (6x² + 9x – 8x – 12)
p(x) = (x – 1) {3x (2x + 3) – 4(2x + 3)}
p(x) = (x – 1) (3x – 4) (2x + 3).

Polynomials Class 9 Extra Questions HOTS

Question 1.
What must be added to polynomial f(x) = x⁴ + 2x² – 2x² + x – 1 so that resulting polynomial is exactly divisible by x² + 2x – 3?
Solution:

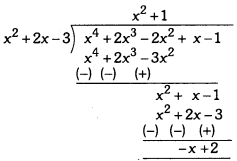
Here, remainder = -x + 2
To make remainder = 0, we must add -(remainder) in the polynomial
i.e., -(-x + 2) i.e., x – 2
Hence, x4 + 2x³ – 2x² + x – 1 + (x – 2)
Here, polynomial = x⁴ + 2x³– 2x² + 2x – 3 and required addition is (x – 2).

Question 2.
If x = 2 – √3, y = √3 – √7 and 2 = √7 – √4, find the value of x’ + 43 + 2?.
Solution:
Here, x + y + z = 2 – √3+ √3 – √7+√7 – 2 = 0
x³+ √3 + x³= 3(x)(y)(z)
= 3(2 – √3)(√3 – √7)(√7 – 2)
= 3(2√3 – 2√7 – 3 + √21)(√7 – 2)
= 3(2√21 – 14 – 3√7 + 7√3 – 4√3 + 4√7 + 6 – 2√21)
= 3(3√3 + √7 – 8)

Question 3.
If (x – a) is a factor of the polynomials x² + px – q and x² + rx – t, then prove that a = \(\frac{t-q}{r-p}\)
Solution:
Let f(x) = x + px -q and g(x) = x² + x – t
Since x-a is factor of both f(x) and g(x)
⇒ f(a) = g(a) = 0
Now, here f(a) = a² + pa – q and
g(a) = a² + ra- t
⇒ a² + pa – q = a + ra – t (considering f(a) = g(a)]
⇒ pa – q = ra – t
⇒ ra – pa = t – q
⇒ a(r – p) = t – q
a = \(\frac{t-q}{r-p}\)

Polynomials Class 9 Extra Questions Value Based (VBQs)

Question 1.
If a teacher divides a material of volume 27x³ + 54x² + 36x + 8 cubic units among three students. Is it possible to find the quantity of material ? Can you name the shape of the figure teacher obtained ? Which value is depicted by the teacher ?
Solution:
We know that, √olume = Length × Breadth × Height
Now, 27x³+ 54x² + 36x + 8
= (3x)³ + 3(3x)²(2) + 3(3x)(2)² + (2)³
= (3x + 2)² = (3x + 2) (3x + 2) (3x + 2)
Thus, volume = (3x + 2) (3x + 2) (3x + 2)
Yes, it is possible to find the quantity of material. (3x + 2) units.
Cube.
Apply knowledge and use of example for clarity of subject, student friendly.

Question 2.
In a camp organised by the students of class-9 to donate amount collected to flood victims of Kashmir. At the time of payment of a juice glass at one stall of juice, stall holder asked the students to pay the remainder of x³+ 3x² + 3x + 1 divided by \(\left(x-\frac{1}{2}\right)\) What is the price of the juice at the stall ? Which value is depicted by class-9 students by organising such camps ?
Solution:
Let
p(x) = x² + 3x² + 3x + 1 and

By long division method, we have

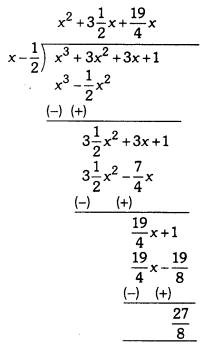
Remainder = \(\frac{27}{8}\) or 3 \(\frac{3}{8}\)
Thus, price of the juice glass is ₹ 3 \(\frac{3}{8}\)
Caring, kindness, social welfare and helping in development of the needy.