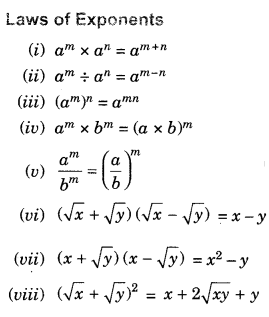On this page, you will find Number Systems Class 9 Notes Maths Chapter 1 Pdf free download. CBSE NCERT Class 9 Maths Notes Chapter 1 Number Systems will seemingly help them to revise the important concepts in less time.
CBSE Class 9 Maths Chapter 1 Notes Number Systems
Number Systems Class 9 Notes Understanding the Lesson
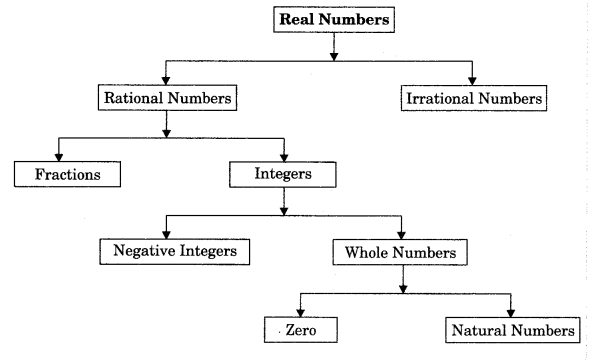
1. Number: A number is a mathematical object which is used in counting and measuring.
2. Number system: A number system defines a set of values used to represent a quantity.
3. Natural numbers: A set of counting numbers is called the natural numbers.
N = {1,2, 3, 4, 5,…}
These are infinite in number. Here first natural number is 1 whereas there is no last natural number.
4. Whole numbers: A set of natural numbers including zero is called the whole numbers.
W = {0, 1, 2, 3, 4, 5,…}
Note: All natural numbers are whole numbers but all whole numbers are not natural numbers.
Integers: A set of all whole numbers including negative of all the natural numbers.
Z = {…, – 7, – 6, – 5, – 4, – 3, – 2, – 1, 0, 1, 2, 3, 4, 5, 6, 7, …}
5. Rational Numbers
A number is called rational number if it can be expressed in the form of \(\frac{p}{q}\), where p and q are integers and q≠ 0.
Example: \(\frac{1}{2}, \frac{2}{3}, \frac{3}{4}, \frac{7}{9}, \text { etc. }\)
Note:
- Every fractional number and integer is a rational number because they can be expressed in the form\(\frac{p}{q}\)
- Between two rational numbers, infinite number of rational numbers can be possible. A rational number between two rational numbers a and b can be found as \(\frac{1}{2}\)(a + b)by using mean method.
- The sum, difference and product of the rational numbers is always a rational number.
- The quotient of a division of one rational number by a non-zero rational number is a rational number.
6. Types of Rational Numbers
1. The natural numbers form a subset of the integers.
2. Natural numbers with zero are referred to as non-negative integers.
3. The natural numbers without zero are known as positive integers.
4. When negative of a positive integer is added to the corresponding positive integer then it produces 0.
- Terminating decimal: It has a finite number of digits after the decimal point.
\(\frac{3}{8}\)=0.375 - Non-terminating recurring decimal or repeating decimal: It has a digit or group of digits after the decimal point that repeat endlessly.
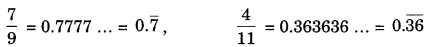
7. Irrational Numbers
Those numbers which cannot be expressed in the form of \(\frac{p}{q}\), where p and q are integers and
q ≠0. They neither terminate nor do they repeat. They are also known as non-terminating non-repeating numbers. Example: \(\sqrt{2}, \sqrt{3}, \sqrt{5}, \sqrt{7}, \sqrt{13}, \sqrt{\frac{7}{3}}, \ldots 5+\sqrt{7}\) are irrational numbers.
An irrational number between two rational numbers a and b can be found as the square root of their product \(\sqrt{a b}\)
Note:
- Euler’s number ‘e’ is an irrational whose first few digits are 2.71828….
- The sum, difference, multiplication and division of irrational numbers are not always irrational.
- Rational number and irrational number can be represented on a number line.
- Irrational numbers like \(\sqrt{2}, \sqrt{3}, \sqrt{5}\) etc. can be represented on a number line by using Pythagoras theorem.
8. Number line: A number line is a line which represent all the numbers. It is a picture of a straight line on which every point is assumed to correspond to a real number and every real number to a point.
![]()
9. Real Numbers”
The union of the set of rational numbers and the set of irrational numbers.
A group of rational or irrational numbers is called real numbers. It can be represented on a number line.
10. Successive Magnification
- Let us suppose we locate 4.46 on the number line. We know 4.46 lies between 4 and 5.
- Now let us divide the portion between 4 and 5 into 10 equal parts and represent 4.1, 4.2, 4.3, …, 4.9.
- We know that 4.46 lies between 4.4 and 4.5 so further divide the portion into 10 equal parts, then these points will represent 4.41, 4.42, 4.43, …, 4.49 on number line. Thus we can locate the given number 4.46 on the number line.