ML Aggarwal Class 8 Solutions for ICSE Maths Model Question Paper 6
Questions 1 to 8 is of 1 mark each.
Question 1.
If x + y = 11 and xy = 24, then x2 + y2 =
(a) 121
(b) 73
(c) 48
(d) none of these
Solution:
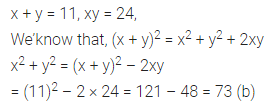
Question 2.
Factors of a3 – 64a are
(a) a(a – 8)2
(b) (a + 8) (a – 8)
(c) a(a + 8) (a – 8)
(d) a(a + 8)2
Solution:
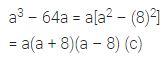
Question 3.
If 3(y – 3) = 5(2y + 1) then y is equal to
(a) 3
(b) -3
(c) 2
(d) -2
Solution:
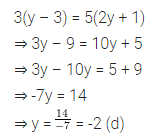
Question 4.
If one angle of a parallelogram is 30° less than other angles, then the larger angle is
(a) 150°
(b) 75°
(c) 105°
(d) 210°
Solution:
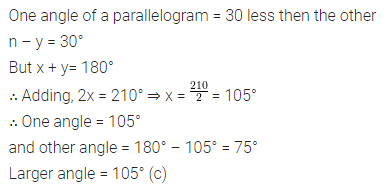
Question 5.
A polyhedron has 7 faces, 10 vertices and 15 edges. Name of the polyhedron is
(a) hexagonal prism
(b) pentagonal prism
(c) hexagonal pyramid
(d) none of these
Solution:

Question 6.
The base of a triangle is twice its height. If the area of the triangle is 25 cm2, then the base is
(a) 10 cm
(b) 20 cm
(c) 5 cm
(d) 25 cm
Solution:

Question 7.
From a well-shuffled deck of 52 playing cards, one card is drawn at random then the probability that card drawn is a blackjack
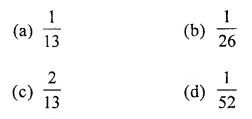
Solution:

Question 8.
Amongst the following digits, the one having exactly one line of symmetry is
(a) 0
(b) 3
(c) 6
(d) 8
Solution:
![]()
Section-B
Questions 9 to 14 are of 2 marks each.
Question 9.
Using a suitable identity, evaluate (9.7)2.
Solution:
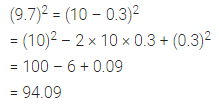
Question 10.
Factorize x2y2(a4 + b4) + a2b2(x4 + y4).
Solution:
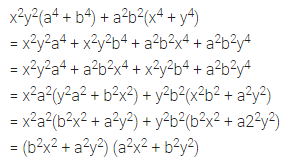
Question 11.
Sum of three consecutive odd numbers is 153. Find the numbers.
Solution:
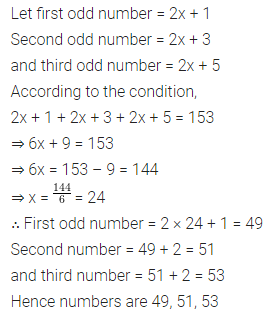
Question 12.
If each interior angle of a regular polygon is 108°, then find the number of sides of the polygon.
Solution:

Question 13.
Verify Euler’s formula for a decagonal pyramid.
Solution:

Question 14.
A cuboid is of dimensions 24 cm × 30 cm × 36 cm. How many small cubes with side 6 cm can be placed in the cuboid?
Solution:

Section-C
Questions 15 to 24 are of 4 marks each.
Question 15.
Simplify the following expressions and evaluate it when x = 1, y = -1
(5xy – 3x2 + 2y2) × (5y2 – 8xy + 3x2) + 9x3y – 8y4 + 12x4
Solution:
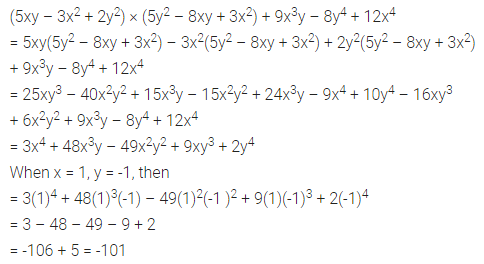
Question 16.
Factorize: 15(2x – 3y)2 – 4(4x – 6y) – 16
Solution:
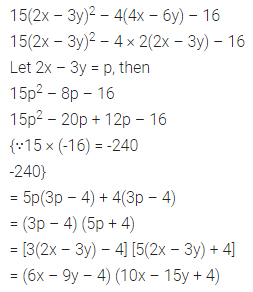
Question 17.
Two years ago Ramesh was three times as old as his son. Two years later, twice of his age will be equal to the five times that of his son’s age. Find their present ages.
Solution:
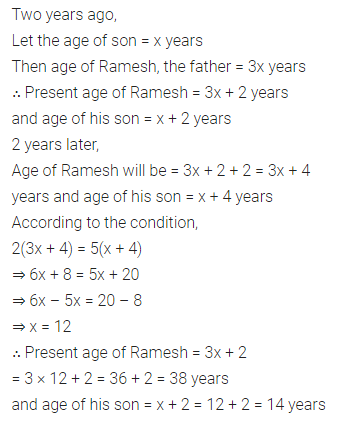
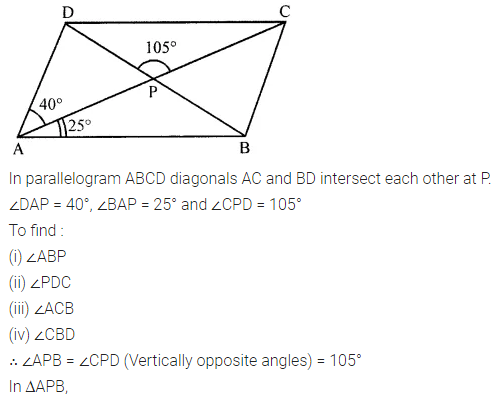
Question 18.
In the given figure ABCD is a parallelogram in which ∠DAP = 40°, ∠BAP = 25° and ∠CPD = 105°, find
(i) ∠ABP
(ii) ∠PDC
(iii) ∠ACB
(iv) ∠CBD
Solution:

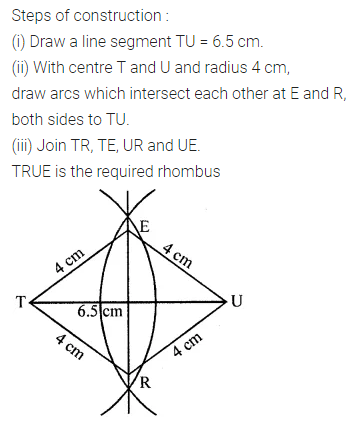
Question 19.
Construct a rhombus TRUE whose one side TR = 4 cm and diagonal TU = 6.5 cm.
Solution:
Question 20.
Construct a parallelogram GOLD in which diagonal GL = 3.8 cm, diagonal OD = 4.6 cm and angle between diagonals is 60°.
Solution:
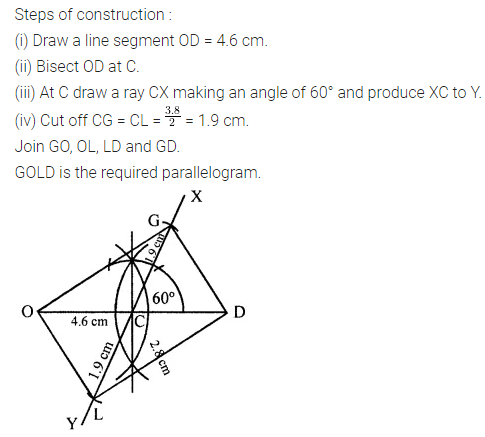
Question 21.
In the given figure, O is the centre of the circle. If PT is tangent to the circle at point T, find the size of each lettered angle.
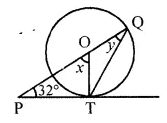
Solution:

Question 22.
A rectangular sheet of tin foil of size 30 cm × 18 cm can be rolled to form a cylinder two ways along length and breadth. Find the ratio of volumes of the two cylinders thus formed.
Solution:
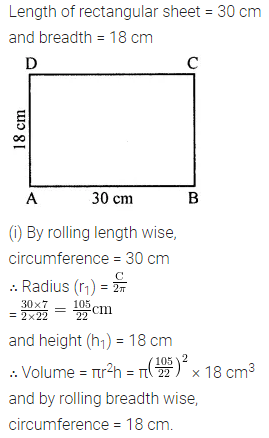

Question 23.
Construct a histogram for the following data:

Solution:

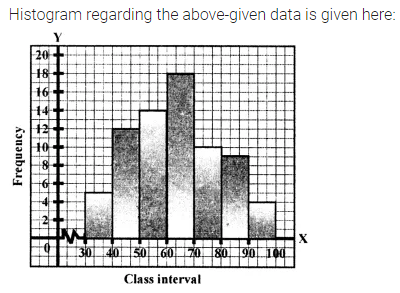
Question 24.
Height of a room is half of its length and its breadth is \(\frac{3}{2}\) of the height. If the cost of painting its four walls at the rate of ₹1.75 per m2 is ₹ 196, then find the cost of tiling the floor of the room at the rate of ₹8.50 per m2.
Solution:
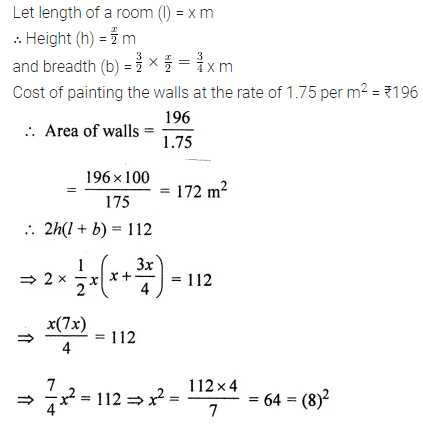

Section-D
Questions 25 to 29 are of 6 marks each.
Question 25.
If \(x+\frac{1}{x}=5\), them find

Solution:
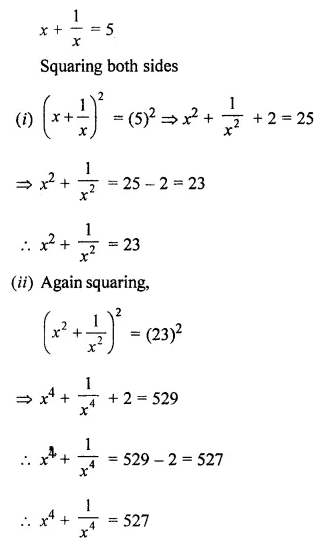
Question 26.
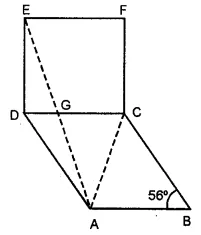
In the given figure, ABCD is a rhombus and DCFE is a square, If ∠ABC = 56°, find
(i) ∠DAG
(ii) ∠FEG
(iii) ∠AGC
Solution:

Question 27.
The figure given below shows a field with the measurement given in metres. Find the area of the field.
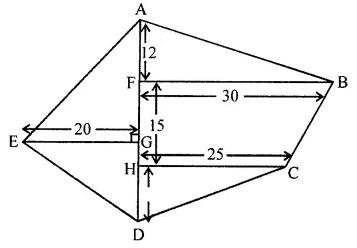
Solution:

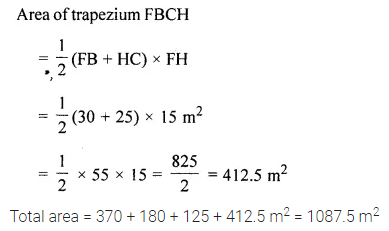
Question 28.
A bag contains 5 red, 6 black and 4 white balls. A ball is drawn at random from the bag. Find the probability that the ball drawn is
(i) white
(ii) not black
(iii) red or black
Solution:

Question 29.
A school decided to award prizes to their students for three values, honesty, punctuality and obedience. The value of prize for punctuality is \(\frac{5}{6}\) of the value of prize for honesty and value of prize for obedience is \(\frac{4}{5}\) of the value of prize for punctuality. If the total value of the three prizes is ₹1500, find the value of each prize. Which quality you prefer to be rewarded most and why? What values are being promoted?
Solution:
