ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 3 Squares and Square Roots Ex 3.2
Question 1.
Write five numbers which you can decide by looking at their one’s digit that they are not square numbers.
Solution:

Question 2.
What will be the unit digit of the squares of the following numbers?
(i) 951
(ii) 502
(iii) 329
(iv) 643
(v) 5124
(vi) 7625
(vii) 68327
(viii) 95628
(ix) 99880
(x) 12796
Solution:

Question 3.
The following numbers are obviously not perfect. Give reason.
(i) 567
(ii) 2453
(iii) 5298
(iv) 46292
(v) 74000
Solution:

Question 4.
The square of which of the following numbers would be an odd number or an even number? Why?
(i) 573
(ii) 4096
(iii) 8267
(iv) 37916
Solution:

Question 5.
How many natural numbers lie between the square of the following numbers?
(i) 12 and 13
(ii) 90 and 91
Solution:
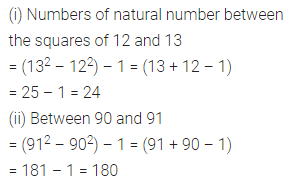
Question 6.
Without adding, find the sum.
(i) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15
(ii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23 + 25 + 27 + 29
Solution:
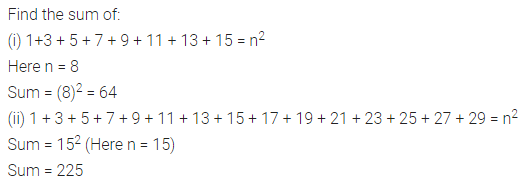
Question 7.
(i) Express 64 as the sum of 8 odd numbers.
(ii) 121 as the sum of 11 odd numbers.
Solution:
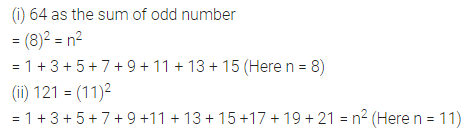
Question 8.
Express the following as the sum of two consecutive integers:
(i) 192
(ii) 332
(iii) 472
Solution:

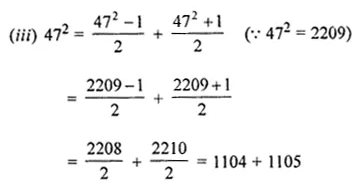
Question 9.
Find the squares of the following numbers without actual multiplication:
(i) 31
(ii) 42
(iii) 86
(iv) 94
Solution:
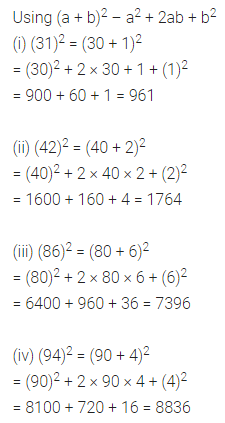
Question 10.
Find the squares of the following numbers containing 5 in unit’s place:
(i) 45
(ii) 305
(iii) 525
Solution:
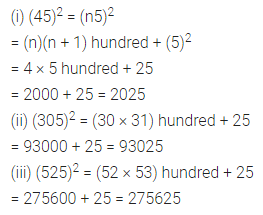
Question 11.
Write a Pythagorean triplet whose one number is
(i) 8
(ii) 15
(iii) 63
(iv) 80
Solution:


Question 12.
Observe the following pattern and find the missing digits:
212 = 441
2012 = 40401
20012 = 4004001
200012 = 4 – – – 4 – – – 1
2000012 = ————–
Solution:

Question 13.
Observe the following pattern and find the missing digits:
92 = 81
992 = 9801
9992 = 998001
99992 = 99980001
999992 = 9——–8———01
9999992 = 9——–0———1
Solution:

Question 14.
Observe the following pattern and find the missing digits:
72 = 49
672 = 4489
6672 = 444889
66672 = 44448889
666672 = 4 ———–8 ————– 9
6666672 = 4———–8————8 –
Solution:
