ML Aggarwal Class 7 Solutions for ICSE Maths Model Question Paper 6 acts as the best resource during your learning and helps you score well in your exams.
ML Aggarwal Class 7 ICSE Maths Model Question Paper 6
(Based on Chapters 10 to 17)
Time allowed: 2\(\frac { 1 }{ 2 }\) Hours
Maximum Marks: 90
General Instructions
- All questions are compulsory.
- The question paper consists of 29 questions divided into four sections A, B, C, and D.
- Section A comprises of 8 questions of 1 mark each.
- Section B comprises of 6 questions of 2 marks each.
- Section C comparises of 10 questions of 4 marks each.
- Section D comprises of 5 questions of 6 marks each.
- Question numbers 1 to 8 in Section A is multiple choice questions where you are to select one correct option out of the given four.
Section – A
Question numbers 1 to 8 is of 1 mark each.
Question 1.
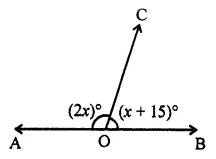
In the given figure, if ∠AOC and ∠COB form a linear pair, then the value of x
(a) 60
(b) 55
(c) 50
(d) 45
Solution:
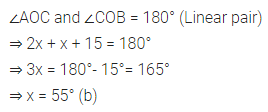
Question 2.
An exterior angle of a triangle is 118°. If one of the two interior opposite angle is 54°, then the other interior opposite angle is
(a) 62°
(b) 54°
(c) 64°
(d) 59°
Solution:
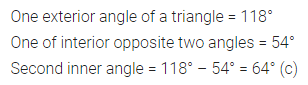
Question 3.
In a right-angled triangle, the lengths of two legs are 8 cm and 15 cm. The length of the hypotenuse is
(a) 23 cm
(b) 20 cm
(c) 17 cm
(d) 17 m
Solution:

Question 4.
If ΔABC = ΔPRQ, the the correct statement is
(a) AB = PQ
(b) ∠B = ∠Q
(c) ∠C = ∠R
(d) AC = PQ
Solution:

Question 5.
The number of lines that can be drawn parallel to a given line l through a point outside the line l is
(a) 0
(b) 1
(c) 2
(d) infinitely many
Solution:
![]()
Question 6.
If the area of a circle is numerically equal to its circumference, then the diameter of the circle is
(a) 2 units
(b) 4 units
(c) 6 units
(d) 8 units
Solution:
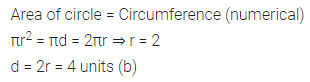
Question 7.
A quadrilateral having exactly two lines of symmetry and rotational symmetry of order 2 is a
(a) square
(b) parallelogram
(c) rhombus
(d) kite
Solution:

Question 8.
A mode is the observation of the data
(a) whose position is in the middle
(b) having maximum value
(c) occurring a maximum number of times
(d) occurring a minimum number of times
Solution:

Section – B
Question numbers 9 to 14 are of 2 marks each.
Question 9.
An angle is 30° more than one-half of its complement. Find the angle.
Solution:

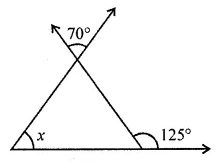
Question 10.
In the given figure, find the value of x.
Solution:
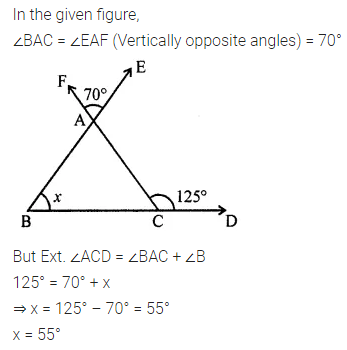
Question 11.
A die is thrown once. Find the probability of getting
(i) a prime number
(ii) a composite number
Solution:

Question 12.
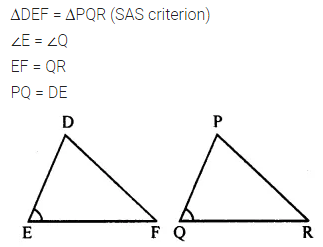
You want to show that ΔDEF = ΔPQR by SAS congruence rule.
It is given that ∠E = ∠Q, you need to have
(i) EF = …….
(ii) PQ = ………
Solution:
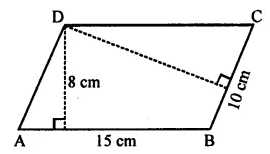
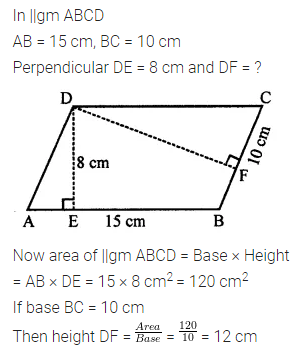
Question 13.
In the given figure, two adjacent sides of a parallelogram are 15 cm and 10 cm. If the distance between the longer sides is 8 cm, find the
(i) area of parallelogram
(ii) the distance between the shorter sides.
Solution:
Question 14.
Find the mean age of six students whose ages (in years) are:
15, 13, 16, 13, 14, 16.
Solution:
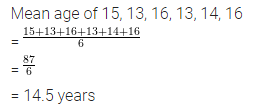
Section – C
Question numbers 15 to 24 are of 4 marks each.
Question 15.
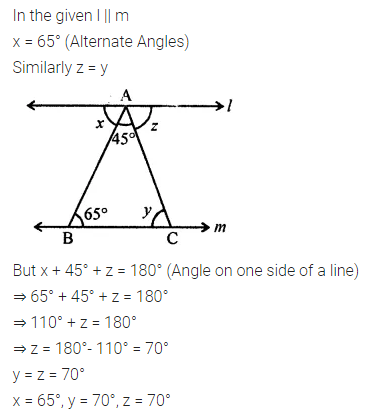
In the given figure, lines l and m are parallel. Find the values of x, y, and z.
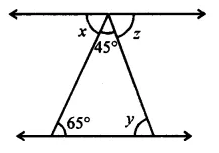
Solution:
Question 16.
In the given figure, BC = AC. Find the value of x.
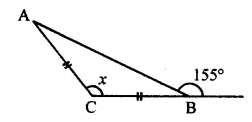
Solution:

Question 17.
If the lengths of the two sides of a triangle are 6 cm and 8.5 cm, then what can be the length of the third side?
Solution:
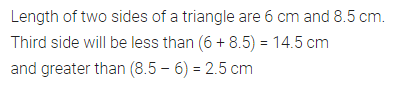
Question 18.
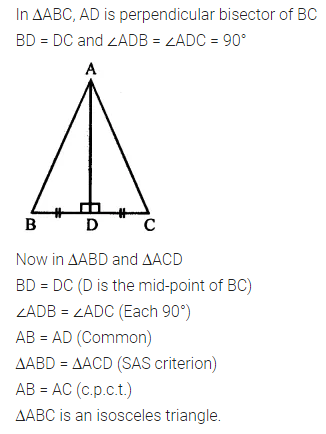
In the given figure, AD is perpendicular bisector of \(\bar { BC }\).
(i) State three pairs of equal parts in ∆ABD and ∆ACD.
(ii) Is ∆ABD = ∆ACD? Give reasons.
(iii) Is ABC an isosceles triangle? Give reasons.
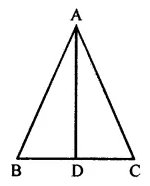
Solution:
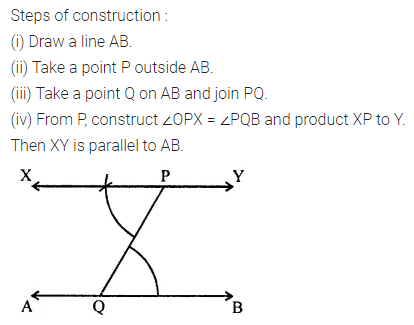
Question 19.
Draw a line, say AB, take a point P outside line AB. Through P, draw a line parallel to line AB using ruler and compasses only.
Solution:
Question 20.
In the given figure, ABCD is a rectangle with AB = 20 cm and BC = 14 cm. Two semicircles are cut from each of two breadths as diameters. Find
(i) the area of the shaded region
(ii) the perimeter of the shaded region.
Take π = \(\frac { 22 }{ 7 }\).
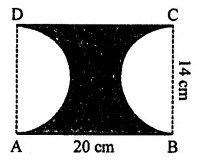
Solution:

Question 21.
Draw the reflection of the letter E in the given mirror line shown dotted.

Solution:

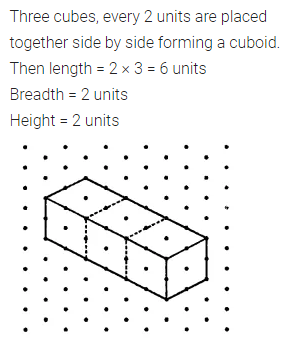
Question 22.
Three cubes each with edge 2 units are placed side by side to form a cuboid. Find the dimensions of the cuboid so formed and draw an isometric sketch of this cuboid.
Solution:
Question 23.
Draw two nets of a regular tetrahedron.
Solution:
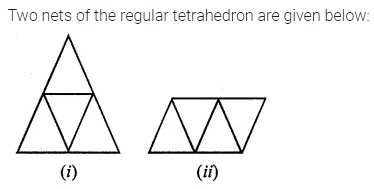
Question 24.
A boy scored the following marks in various class tests during a year, each test is marked out of 20:
15, 17, 16, 7, 9, 12, 14, 16, 3, 19, 12, 16
(i) Arrange the marks in ascending order.
(ii) What are his modal marks?
(iii) What are his median marks?
(iv) What are his mean marks?
Solution:

Section – D
Question numbers 25 to 29 are of 6 marks each.
Question 25.
In the given figure, all measurements are in centimeters. If AD is perpendicular to BC, find the length of B.
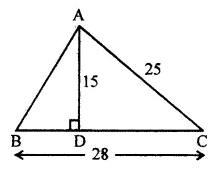
Solution:

Question 26.
In the adjoining figure, show that ΔABC = ΔDBC. Hence, find the values of x and y.
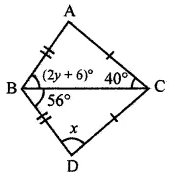
Solution:
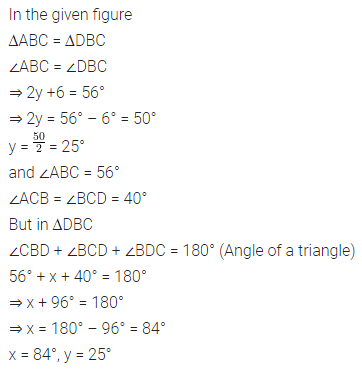
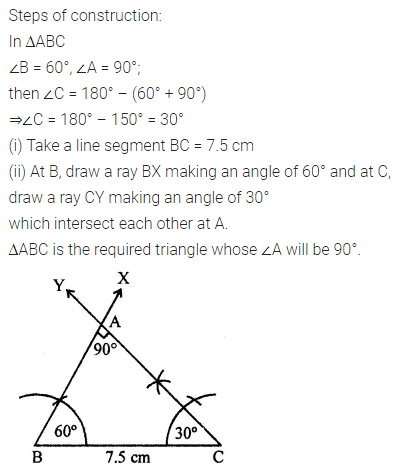
Question 27.
By using ruler and compasses only, construct a triangle ABC with BC = 7.5 cm, ∠B = 60° and ∠A = 90°.
Solution:
Question 28.
Anjali took a wire of length 88 cm and bent it into the shape of a circle. Find the area enclosed by that circle. If the same wire is bent in the shape of a square, then find the area enclosed by that square. Which shape encloses more area and by how much?
Take π = \(\frac { 22 }{ 7 }\)
Solution:

Question 29.
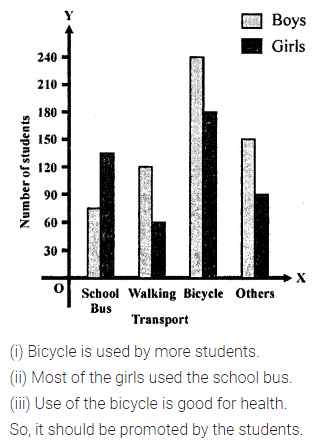
Given below is the data of school going students (boys and girls):

Draw a double bar graph to represent the above data and hence answer the following questions:
(i) Which mode of transport is used by more students?
(ii) Which mode of transport is used by more number of girls that the number of boys?
What values are being promoted by using a bicycle as a mode of transport?
Solution: