ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Ex 7.1
These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Ex 7.1
More Exercises
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Ex 7.1
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Ex 7.2
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Ex 7.3
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion MCQS
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Chapter Test
Question 1.
An alloy consists of \(27 \frac { 1 }{ 2 } \) kg of copper and \(2 \frac { 3 }{ 4 } \) kg of tin. Find the ratio by weight of tin to the alloy
Solution:
Copper = \(27 \frac { 1 }{ 2 } \) kg = \(\\ \frac { 55 }{ 2 } \) kg,
Tin = \(2 \frac { 3 }{ 4 } \) kg = \(\\ \frac { 11 }{ 4 } \) kg
Question 2.
Find the compounded ratio of:
(i) 2 : 3 and 4 : 9
(ii) 4 : 5, 5 : 7 and 9 : 11
(iii) (a – b) : (a + b), (a + b)2 : (a2 + b2) and (a4 – b4) : (a2 – b2)2
Solution:
(i) 2 : 3 and 4 : 9
Compound ratio = \(\\ \frac { 2 }{ 3 } \) x \(\\ \frac { 4 }{ 9 } \)
= \(\\ \frac { 8 }{ 27 } \) or 8 : 27
(ii) 4 : 5, 5 : 7 and 9 : 11
Question 3.
Find the duplicate ratio of
(i) 2 : 3
(ii) √5 : 7
(iii) 5a : 6b
Solution:
(i) Duplicate ratio of 2 : 3 = (2)2 : (3)2 = 4 : 9
(ii) Duplicate ratio of √5 : 7 = (√5)2 : (7)2 = 5 : 49
(iii) Duplicate ratio of 5a : 6b = (5a)2 : (6b)2 = 25a2 : 36b2
Question 4.
Find the triplicate ratio of
(i) 3 : 4
(ii) \(\\ \frac { 1 }{ 2 } \) : \(\\ \frac { 1 }{ 3 } \)
(iii) 13 : 23
Solution:
(i) Triplicate ratio of 3 : 4
= (3)3 : (4)3
= 27 : 64
Question 5.
Find the sub-duplicate ratio of
(i) 9 : 16
(ii) \(\\ \frac { 1 }{ 4 } \) : \(\\ \frac { 1 }{ 9 } \),
(iii) 9a2 : 49b2
Solution:
(i) Sub-duplicate ratio of 9 : 16
= √9 : √16
= 3 : 4
Question 6.
Find the sub-triplicate ratio of
(i) 1 : 216
(ii) \(\\ \frac { 1 }{ 8 } \) : \(\\ \frac { 1 }{ 125 } \)
(iii) 27a3 : 64b3
Solution:
(i) Sub-triplicate ratio of 1 : 216
= \(\sqrt [ 3 ]{ 1 } :\sqrt [ 3 ]{ 216 } \)
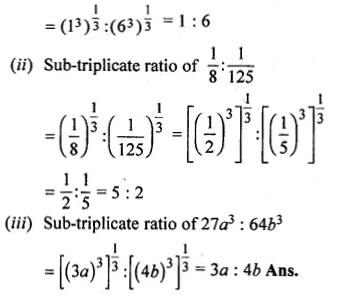
Question 7.
Find the reciprocal ratio of
(i) 4 : 7
(ii) 32 : 42
(iii) \(\frac { 1 }{ 9 } :2 \)
Solution:
(i) Reciprocal ratio of 4 : 7 = 7 : 4
(ii) Reciprocal ratio of 32 : 42 = 42 : 32 = 16 : 9
(iii) Reciprocal ratio of \(\frac { 1 }{ 9 } :2 \) = \(2:\frac { 1 }{ 9 } \) = 18 : 1
Question 8.
Arrange the following ratios in ascending order of magnitude:
2 : 3, 17 : 21, 11 : 14 and 5 : 7
Solution:
Writing the given ratios in fraction
\(\frac { 2 }{ 3 } ,\frac { 17 }{ 21 } ,\frac { 11 }{ 14 } ,\frac { 5 }{ 7 } \)

Question 9.
(i) If A : B = 2 : 3, B : C = 4 : 5 and C : D = 6 : 7, find A : D
(ii) If x : y = 2 : 3, and y : z = 4 : 7, find x : y : z
Solution:
Let A : B = 2 : 3, B : C = 4 : 5 and C : D = 6 : 7
\(\frac { A }{ B } =\frac { 2 }{ 3 } ,\frac { B }{ C } =\frac { 4 }{ 5 } ,\frac { C }{ D } =\frac { 6 }{ 7 } \)
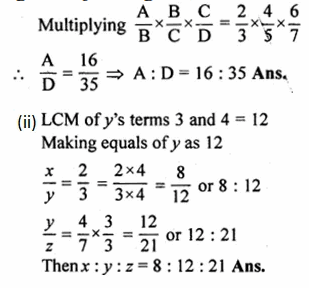
Question 10.
(i) If A: B = \(\frac { 1 }{ 4 } :\frac { 1 }{ 5 } \) and B : C = \(\frac { 1 }{ 7 } :\frac { 1 }{ 6 } \), find A : B : C.
(ii) If 3A = 4B = 6C, find A : B : C
Solution:
A : B = \(\frac { 1 }{ 4 } \times \frac { 5 }{ 1 } =\frac { 5 }{ 4 } \)
B : C = \(\frac { 1 }{ 7 } \times \frac { 6 }{ 1 } =\frac { 6 }{ 7 } \)
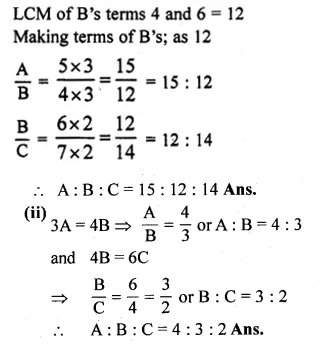
Question 11.
(i) If \(\frac { 3x+5y }{ 3x-5y } =\frac { 7 }{ 3 } \) , Find x : y
(ii) ) If a : b = 3 : 11, find (15a – 3b) : (9a + 5b). a
Solution:
(i) \(\frac { 3x+5y }{ 3x-5y } =\frac { 7 }{ 3 } \)
⇒ 9x + 15y = 21x – 35y [By cross multiplication]
⇒ 21x – 9x = 15y + 35y

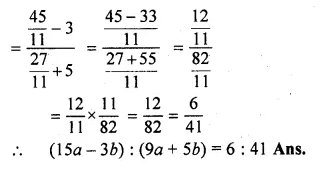 >
>
Question 12.
(i) If (4x² + xy) : (3xy – y²) = 12 : 5, find (x + 2y) : (2x + y).
(ii) If y (3x – y) : x (4x + y) = 5 : 12. Find (x² + y²) : (x + y)².
Solution:
(4x² + xy) : (3xy – y²) = 12 : 5
⇒ \(\frac { { 4x }^{ 2 }+xy }{ 3xy-{ y }^{ 2 } } =\frac { 12 }{ 5 } \)
⇒ 20x² + 5xy = 36xy – 12y²
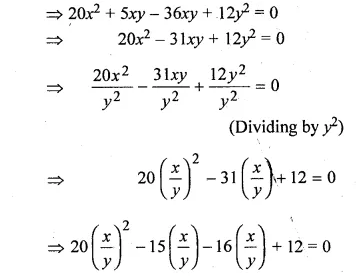
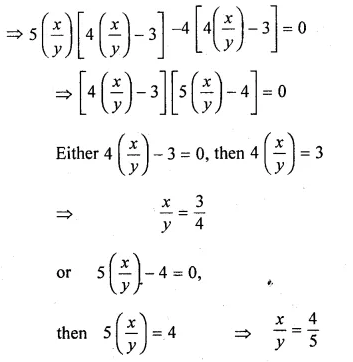
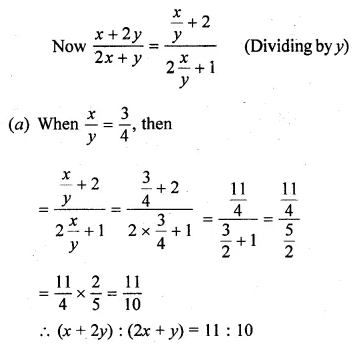

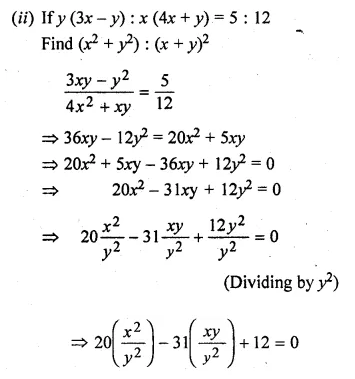
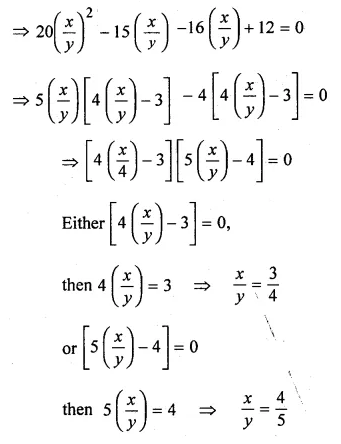
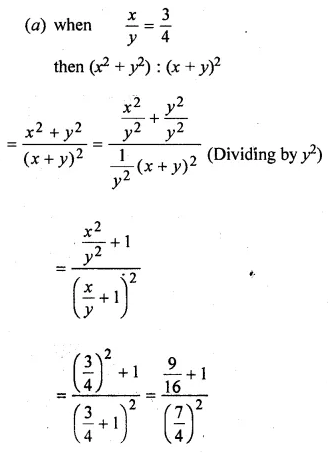
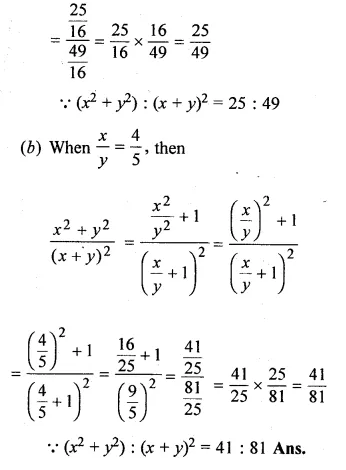
Question 13.
(i) If (x – 9) : (3x + 6) is the duplicate ratio of 4 : 9, find the value of x.
(ii) If (3x + 1) : (5x + 3) is the triplicate ratio of 3 : 4, find the value of x.
(iii) If (x + 2y) : (2x – y) is equal to the duplicate ratio of 3 : 2, find x : y.
Solution:
(i) \(\frac { x-9 }{ 3x+6 } ={ \left( \frac { 4 }{ 9 } \right) }^{ 2 }\)
⇒ \(\frac { x-9 }{ 3x+6 } =\frac { 16 }{ 81 } \)
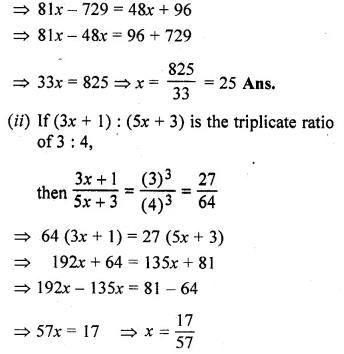
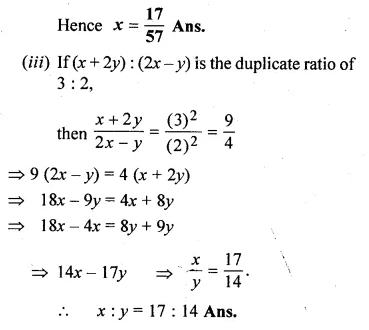
Question 14.
(i) Find two numbers in the ratio of 8 : 7 such that when each is decreased by \(12 \frac { 1 }{ 2 } \), they are in the ratio 11 : 9.
(ii) The income of a man is increased in the ratio of 10 : 11. If the increase in his income is Rs 600 per month, find his new income.
Solution:
(i) The ratio is 8 : 7
Let the numbers be 8x and 7x,
According to condition,
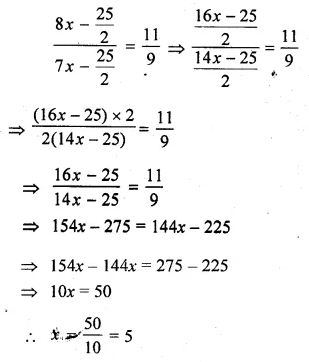

Question 15.
(i) A woman reduces her weight in the ratio 7 : 5. What does her weight become if originally it was 91 kg.
(ii) A school collected Rs 2100 for charity. It was decided to divide the money between an orphanage and a blind school in the ratio of 3 : 4. How much money did each receive?
Solution:
(i) Ratio between the original weight and reduced weight = 7 : 5
Let original weight = 7x
then reduced weight = 5x
If original weight = 91 kg.

Question 16.
(i) The sides of a triangle are in the ratio 7 : 5 : 3 and its perimeter is 30 cm. Find the lengths of sides.
(ii) If the angles of a triangle are in the ratio 2 : 3 : 4, find the angles.
Solution:
(i) Perimeter of a triangle = 30 cm.
Ratio among sides = 7 : 5 : 3
Sum of ratios 7 + 5 + 3 = 15

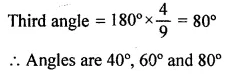
Question 17.
Three numbers are in the ratio \(\frac { 1 }{ 2 } :\frac { 1 }{ 3 } :\frac { 1 }{ 4 } \) If the sum of their squares is 244, find the numbers.
Solution:
The ratio of three numbers \(\frac { 1 }{ 2 } :\frac { 1 }{ 3 } :\frac { 1 }{ 4 } \)
= \(\frac { 6:4:3 }{ 12 } \)
= 6 : 4 : 3
Let first number 6x, second 4x and third 3x
.’. According to the condition
(6x)² + (4x)² + (3x)² = 244
⇒ 36x² + 16x² + 9x² = 244

Question 18.
(i) A certain sum was divided among A, B and C in the ratio 7 : 5 : 4. If B got Rs 500 more than C, find the total sum divided.
(ii) In a business, A invests Rs 50000 for 6 months, B Rs 60000 for 4 months and C, Rs 80000 for 5 months. If they together earn Rs 18800 find the share of each.
Solution:
(i) Ratio between A, B and C = 7 : 5 : 4
Let A’s share = 7x
B’s share = 5x
and C’s share = 4x
Total sum = 7x + 5x + 4x = 16x

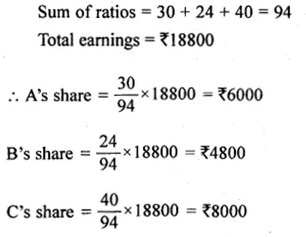
Question 19.
(i) In a mixture of 45 litres, the ratio of milk to water is 13 : 2. How much water must be added to this mixture to make the ratio of milk to water as 3 : 1 ?
(ii) The ratio of the number of boys to the number of girls in a school of 560 pupils is 5 : 3. If 10 new boys are admitted, find how many new girls may be admitted so that the ratio of the number of boys to the number of girls may change to 3 : 2.
Solution:
(i) Mixture of milk and water = 45 litres
Ratio of milk and water =13 : 2
Sum of ratio = 13 + 2 = 15
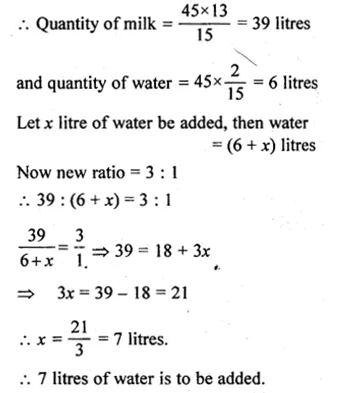
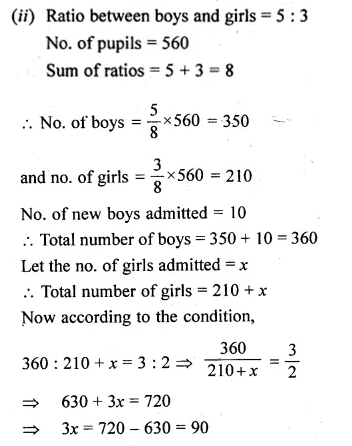
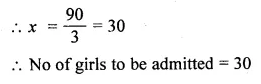
Question 20.
(i) The monthly pocket money of Ravi and Sanjeev are in the ratio 5 : 7. Their expenditures are in the ratio 3 : 5. If each saves Rs 80 every month, find their monthly pocket money.
(ii) In class X of a school, the ratio of the number of boys to that of the girls is 4 : 3. If there were 20 more boys and 12 less girls, then the ratio would have been 2 : 1, How many students were there in the class?
Solution:
(i) Let the monthly pocket money of Ravi and Sanjeev be 5x and 7x respectively.
Also, let their expenditure be 3y and 5y respectively.
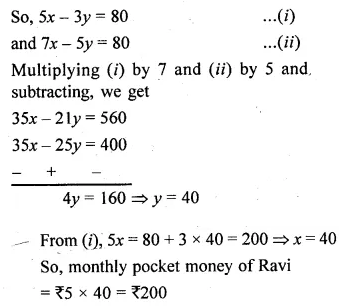
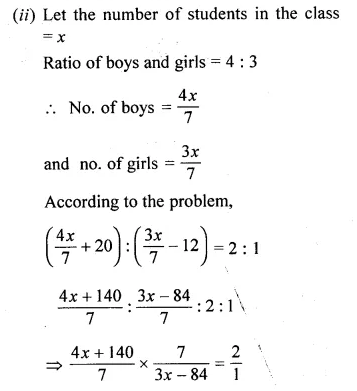
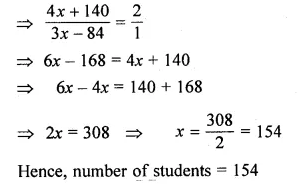
Question 21.
In an examination, the ratio of passes to failures was 4 : 1. If 30 less had appeared and 20 less passed, the ratio of passes to failures would have been 5 : 1. How many students appeared for the examination
Solution:
Let the number of passes = 4x
and number of failures = x
The total number of students appeared = 4x + x = 5x
In the second case, the number of students appeared = 5x – 30
and number of passes = 4x – 20

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Ex 7.1 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.