Heron’s Formula Class 9 Extra Questions Maths Chapter 12 with Solutions Answers

Here we are providing Heron’s Formula Class 9 Extra Questions Maths Chapter 12 with Answers Solutions, Extra Questions for Class 9 Maths was designed by subject expert teachers.

Extra Questions for Class 9 Maths Heron’s Formula with Answers Solutions

Extra Questions for Class 9 Maths Chapter 12 Heron’s Formula with Solutions Answers

Heron’s Formula Class 9 Extra Questions Very Short Answer Type

Question 1.
Find the area of an equilateral triangle having side 6 cm.
Solutioin:
Area of an equilateral triangle = \(\frac{\sqrt{3}}{4}\) × (side)² = \(\frac{\sqrt{3}}{4}\) × 6 × 6 = 9√3 cm²

Question 2.
If the perimeter of an equilateral triangle is 90 m, then find its area.
Solutioin:

Question 3.
If every side of a triangle is doubled, then find the percent increase in area of triangle so formed.
Solutioin:
Let the sides of the given triangle be, a units, b units and c units.

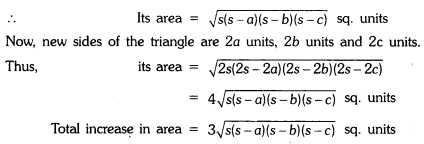
Hence, percent increase = 300%

Question 4.
If the length of a median of an equilateral triangle is x cm, then find its area.
Solutioin:

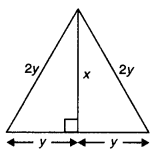
Let each equal sides of given equilateral triangle be 2y². We know that median is also perpendicular bisector.
∴ y² + x² = 4y²
⇒ x² = 3y²
⇒ x = √3y
or
⇒ y = \(\frac{x}{\sqrt{3}}\)
Now, area of given triangle = \(\frac{1}{2}\)
× 2y × X = y × x = \(\frac{x}{\sqrt{3}}\)× x = \(\frac{x^{2}}{\sqrt{3}}\)

Heron’s Formula Class 9 Extra Questions Short Answer Type 2

Question 1.
Find the area of a triangle whose sides are 11 m, 60 m and 61 m.
Solutioin:
Let a = 11 m, b = 60 m and c = 61 m :

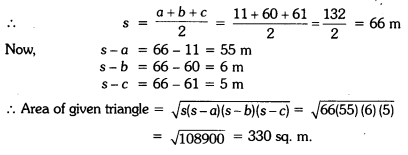
Question 2.
Suman has a piece of land, which is in the shape of a rhombus. She wants her two sons to work on the land and produce different crops. She divides the land in two equal parts by drawing a diagonal. If its perimeter is 400 m and one of the diagonals is of length 120 m, how much area each of them will get for his crops ?
Solutioin:
Here, perimeter of the rhombus is 400 m.
∴ Side of the rhombus = \(\frac{400}{4}\) = 100 m
Let diagonal BD = 120 m and this diagonal divides the rhombus ABCD into two equal parts.

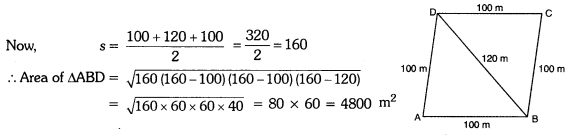
Hence, area of land allotted to two sons for their crops is 4800 m² each.

Question 3.
The perimeter of a triangular field is 144 m and its sides are in the ratio 3:4:5. Find the length of the perpendicular from the opposite vertex to the side whose length is 60 m.
Solutioin:
Let the sides of the triangle be 3x, 4x and 5x
∴ The perimeter of the triangular field = 144 m
⇒ 3x + 4x + 5x = 144
⇒ 12x = 144

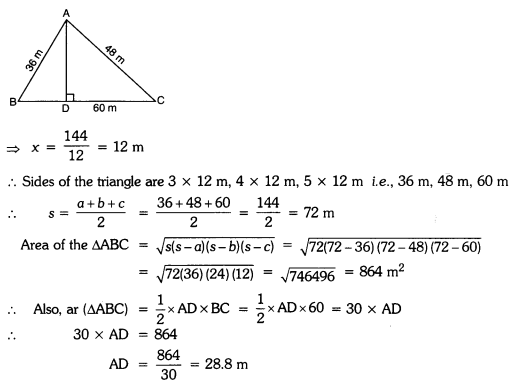
Question 4.
Find the area of the triangle whose perimeter is 180 cm and two of its sides are of lengths 80 cm and 18 cm. Also, calculate the altitude of the triangle corresponding to the shortest side.
Solutioin:
Perimeter of given triangle = 180 cm
Two sides are 18 cm and 80 cm
∴ Third side = 180 – 18 – 80 = 82 cm

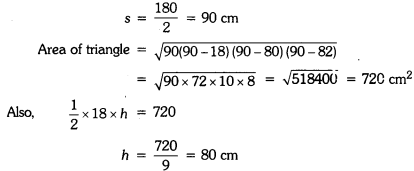
Hence, area of triangle is 720 cm² and altitude of the triangle corresponding to the shortest side is 80 cm.

CBSE Class 10 Maths Formulas for Chapter 4 Quadratic Equations are mentioned in this article.

Heron’s Formula Class 9 Extra Questions Long Answer Type

Question 1.
Calculate the area of the shaded region.

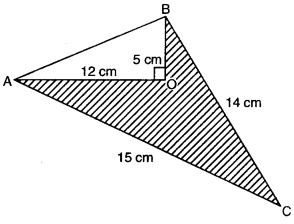
Solutioin:

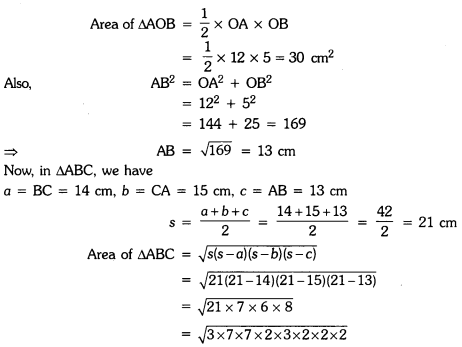
= 2 × 2 × 3 × 7 = 84 cm²
Area of shaded region = Area of ∆ABC – Area of ∆AOB
= 84 cm² – 30 cm² = 54 cm²

Question 2.
The sides of a triangular park are 8 m, 10 m and 6 m respectively. A small circular area of diameter 2 m is to be left out and the remaining area is to be used for growing roses. How much area is used for growing roses ? (use n = 3.14)
Solutioin:
The sides of the triangular park are 8 m, 10 m and 6 m.

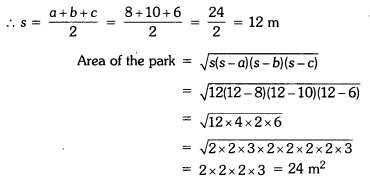
Radius of the circle = \(\frac{2}{2}\) = 1 m
Area of the circle = πr² = 3.14 × 1 × 1 = 3.14 m²
∴ Area to be used for growing roses = Area of the park – area of the circle
= 24 – 3.14 = 20.86 m²

Heron’s Formula Class 9 Extra Questions HOTS

Question 1.
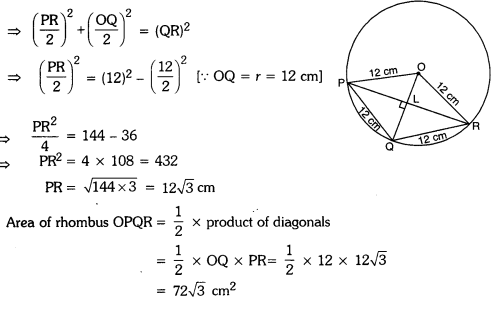
OPQR is a rhombus, whose three vertices P, Q and R lie on the circle with centre 0. If the radius of the circle is 12 cm, find the area of the rhombus.
Solutioin:
Since diagonals bisect each other at 90°.
∴ In right ∆QLR, (LR)² + (LQ)² = (QR)²

Question 2.
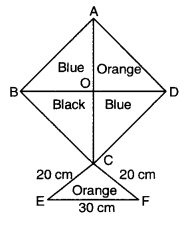
How much paper of each shade is needed to make a kite given in the figure, in which ABCD is a square with diagonal 60 cm?

Solutioin:
Since diagonals of a square are of equal length and bisect each other at right angles, therefore,
Area of ∆AOD = \(\frac{1}{2}\) × 30 × 30 = 450 cm²
Area of ∆AOD = Area of ∆DOC = Area of ∆BOC
= Area of ∆AOB = 450 cm²
[∵ ∆AOD = ∆AOB ≅ ∆BOC ≅ ∆COD, ∵ they² have equal area]
Now, area of ACEF (by Heron’s formula)
Here a = 20 cm, b = 20 cm and c = 30 cm

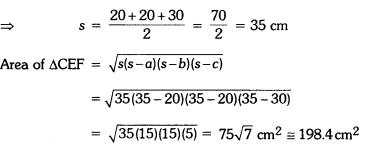
Now, area of orange shaded paper in kite
= Area of ∆AOD + Area of ∆CEF
= 450 cm² + 198.4 cm²
= 648.4 cm²
Area of blue shaded paper in kite
= Area of ∆AOB + Area of ∆COD
= 450 cm² + 450 cm² = 900 cm²
Area of black shaded paper in kite = Area of ∆BOC = 450 cm².

Heron’s Formula Class 9 Extra Questions Value Based (VBQs)

Question 1.
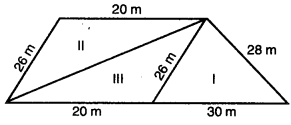
Sister Nivedita has trapezium shaped plot which she divided into three triangular portion for different purposes. I – for providing free education for orphan children, II – for providing dispensary for the needy villagers and III – for the library for villagers. Find the area of trapezium plot given in the figure. Which qualities of sister Nivedita are being depicted in question ?

Solutioin:
Here, ABCD is the trapezium with AB || DC.
Through C, Draw CF ⊥ AB
For – I: For area of ∆EBC

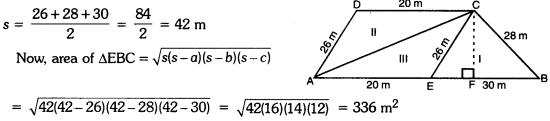
But, we know, Area of ∆EBC = \(\frac{1}{2}\)(base × height)
⇒ \(\frac{1}{2}\)1 × 30 × CF = 336
15 × CF = 336
⇒ CF = \(\frac{336}{15}\) = 22.4 m
Now, area of trapezium shaped plot = \(\frac{1}{2}\) (20 + 50)(22.4)
= 35 x 22.4 = 784 m²
Caring, kind, social, generous and visionary lady.

Question 2.
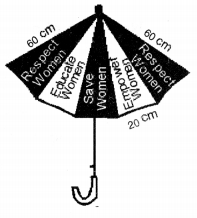
In an exhibition, an umbrella is made by stiching 10 triangular pieces of cloth with same message written on two triangular pieces. If each piece of cloth measures 60 cm, 60 cm and 20 cm, find how much cloth is required for each message.
Why we should respect women, educate women, save women and empower women ?

Solutioin:
Here, each triangular piece is an isosceles triangle with sides 60 cm, 60 cm and 20 cm.

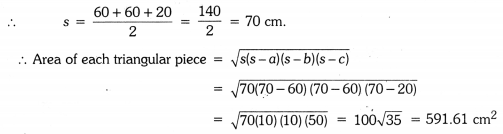
Now, there are 2 triangular pieces with same message.
∴ Total area of cloth for each message = 2 × 591.61 = 1183.22 cm²
We should respect women, educate women, save women and empower women to serve humanity and give them equal opportunity so far they deprived.