Here we are providing Constructions Class 10 Extra Questions Maths Chapter 11 with Answers Solutions, Extra Questions for Class 10 Maths was designed by subject expert teachers.
Extra Questions for Class 10 Maths Constructions with Answers Solutions
Extra Questions for Class 10 Maths Chapter 11 Constructions with Solutions Answers
Constructions Class 10 Extra Questions Very Short Answer Type
Question 1.
Is construction of a triangle with sides 8 cm, 4 cm, 4 cm possible?
Solution:
No, we know that in a triangle sum of two sides of a triangle is greater than the third side. So the condition is not satisfied.
Question 2.
To divide the line segment AB in the ratio 5 : 6, draw a ray AX such that ∠BAX is an acute angle, then draw a ray BY parallel to AX and the point A1, A2, A3… and B1, B2, B3… are located at equal distances on ray AX and BY respectively. Then which points should be joined?
Solution:
A5 and B6.
Question 3.
To draw a pair of tangents to a circle which are inclined to each other at an angle of 60°, it is required to draw tangents at end points of those two radii of the circle. What should be the angle between them?
Solution:
120°
Question 4.
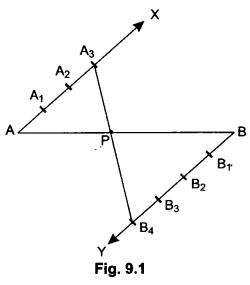
In Fig. 9.1 by what ratio does P divide AB internally.
Solution:
From Fig. 9.1, it is clear that there are 3 points at equal distances on AX and 4 points at equal distances on BY. Here P divides AB on joining A3 B4. So P divides internally by 3 : 4.
Question 5.
Given a triangle with side AB = 8 cm. To get a line segment AB’ = 2 of AB, in what ratio will line segment AB be divided?
Solution:
Given AB = 8 cm
AB’ = \(\frac{3}{4}\) of AB
= \(\frac{3}{4}\) × 8 = 6 cm
BB’ = AB – AB’ = 8 – 6 = 2 cm.
⇒ AB’: BB’ = 6 : 2 = 3 : 1
Hence the required ratio is 3 : 1.
Constructions Class 10 Extra Questions Short Answer Type I and II
Question 1.
Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are \(\frac{2}{3}\) of the corresponding sides of the first triangle.
OR
Draw a triangle with sides 4 cm, 5 cm and 6 cm. Then construct another triangle whose sides are \(\frac{2}{3}\) of the corresponding sides of first triangle.
Solution:
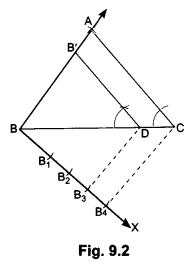
Steps of Construction:
Step I: Draw a line segment BC = 6 cm
Step II: Draw an arc with B as centre and radius equal to 5 cm.
Step III: Draw an arc, with C as centre and radius equal to 4 cm intersecting the previous drawn arc at A.
Step IV: Join AB and AC, then ∆ABC is the required triangle.
Step V: Below BC make an acute angle CBX
Step VI: Along BX mark off three points at equal distance: B1, B2, B3, such that BB1 = B1B2, = B2B3.
Step VII: Join BC3.
Step VIII: From B2, draw B2, D || B3,C, meeting BC at D.
Step IX: From D draw ED || AC meeting BA at E. Then we have ∆EDB which is the required triangle.
Justification:
Since DE || CA
![]()
Hence, we have the new AEBD similar to the given ∆ABC, whose sides are equal to \(\frac{2}{3}\) of the corresponding sides of ∆ABC.
Question 2.
Draw a line segment of length 7.6 cm and divide it in the ratio 5 : 8. Measure the two parts.
Solution:
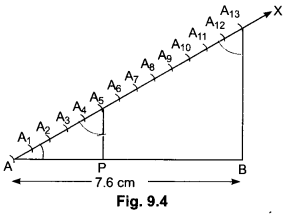
Steps of Construction:
Step I: Draw a line segment AB = 7.6 cm
Step II: Draw any ray AX making an acute angle ∠BAX with AB.
Step III: On ray AX starting from A, mark 5 + 8 = 13 equal arcs. AA1, A1A2, A2A3, A3A4, … A11A12, and A12A13.
Step IV: Join A13B.
Step V: From A5, draw A5P || A13B, meeting AB at P. Thus, P divides AB in the ratio 5 : 8. On measuring the two parts. We find AP = 2.9 cm and PB = 4.7 cm (approx).
Justification:
In ∆ABA13, PA5 || BA13 .
∴ By Basic Proportionality Theorem
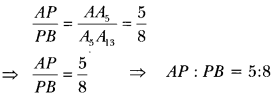
Question 3.
Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then draw another triangle whose sides are 1\(\frac{1}{2}\) times the corresponding sides of the isosceles triangle.
Solution:
Steps of Construction:
Step 1: Draw BC = 8 cm.
Step II: Construct XY, the perpendicular bisector of line segment BC, meeting BC at M.
Step III: Along MP, cut-off MA = 4 cm.
Step IV: Join BA and CA. Then ∆ABC so obtained is the required ∆ABC.
Step V: Extend BC to D, such that BD = 12 cm
Step VI: Draw DE || CA meeting BA produced at E. Then AEBD is the required triangle.
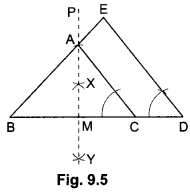
Justification:
Since, DE || CA .
![]()
Hence, we have the new triangle similar to the given triangle whose sides are 1 \(\frac{1}{2}\) i.e, \(\frac{3}{2}\) times the corresponding sides of the isosceles ABC.
Question 4.
Draw a triangle ABC with side BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then construct a triangle whose sides of the corresponding sides of the triangle ABC.
Solution:
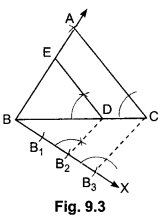
Steps of Construction:
Step 1: Construct a ∆ABC in which BC = 6 cm and, AB = 5 cm and ∠ABC = 60°.
Step II: Below BC make an acute ∠CBX.
Step III: Along BX mark off four arcs: B1, B2, B3 such that BB1 = B1B2 = B2B3 = B3B4.
Step IV: Join B4C.
Step V: From B3, draw B3D || B4C, meeting BC at D.
Step VI: From D, draw ED || AC, meeting BA at E.
Now, we have AEBD which is the required triangle whose sides are \(\frac{3}{4}\)th of the corresponding sides of ∆ABC.
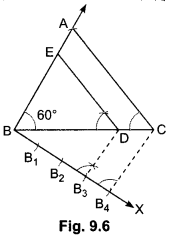
Justification:
Here, DE || CA
∴ ∆ABC ~ ∆EBD.
![]()
Hence, we get the new triangle similar to the given triangle whose sides are equal to \(\frac{3}{4}\)th of the corresponding sides of ∆ABC.
Question 5.
Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.
Solution:
Steps of Construction:
Step 1: Take a point O and draw a circle of radius 6 cm.
Step II: Take a point P at a distance of 10 cm from the centre 0.
Step III: Join OP and bisect it. Let M be the mid-point.
Step IV: With M as centre and MP as radius, draw a circle to intersect the circle at Q and R.
Step V: Join PQ and PR. Then, PQ and PR are the required tangents. On measuring, we find, PQ = PR = 8cm.
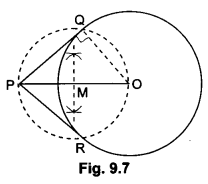
Justification:
On joining OQ, we find that ∠PQO = 90°, as ∠PQO is the angle in the Semicircle.
∴ PQ ⊥ OQ
Since OQ is the radius of the given circle, PQ has to be a tangent to the circle. Similarly, PR is
also a tangent to the circle.
Question 6.
Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also, verify the measurement by actual calculation.
Solution:
Steps of Construction:
Step 1: Take a point O and draw a circle of radius OA = 4 cm. Also, draw a concentric circle of radius OB = 6 cm
Step II: Find the mid-point C of OB and draw a circle of radius OC = BC. Suppose this circle intersects the circle of radius 4 cm at P and Q.
Step III: Join BP and BQ to get the desired tangents from a point B on the circle of radius 6 cm. By actual measurement, we find BP = BQ = 4.5 cm.
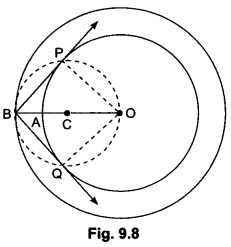
Justification:
In ∆BPO, we have
∠BPO = 90°, OB = 6 cm and OP = 4 cm
∴ OB2 = BP2 + OP2 [Using Pythagoras theorem]
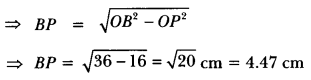
Similarly, BQ = 4.47 cm
Question 7.
Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and
taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.
Solution:
Steps of Construction:
Step I: Draw a line segment AB = 8 cm.
Step II: With A as centre, draw a circle of radius 4 cm and let it intersect the line segment AB in M.
Step III: With B as centre, draw a circle of radius 3 cm.
Step IV: With M as centre, draw a circle of radius AM and let it intersect the given two circles in P, e and R, S.
Step V: Join AP, AQ, BR and BS.
These are the required tangents.
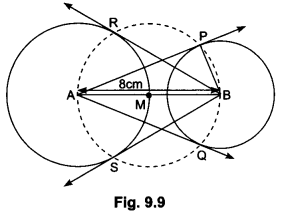
Justification:
On joining BP, we have ∠BPA = 90°, as ∠BPA is the angle in the semicircle.
∴ AP ⊥ PB
Since BP is the radius of given circle, so AP has to be a tangent to the circle. Similarly, AQ, BR and BS are the tangents.
Constructions Class 10 Extra Questions Long Answer Type
Question 1.
Construct a triangle similar to a given triangle ABC with its sides equal to \(\frac{5}{3}\) of the corresponding sides of the triangle ABC (i.e., of scale factor ).
Solution:
Steps of Construction:
Step I: Draw any ray BX making an acute angle with BC on the side opposite to the vertex A.
Step II: From B cut off 5 arcs
B1, B2, B3, B4 and B5 on BX so that
BB1 = B1B2 = B2B3 = B3B4 = B4B5.
Step III: Join B3 to C and draw a line through B5, parallel to B3C intersecting the extended line segment BC at C’.
Step IV: Draw a line through C’ parallel to CA intersecting the
extended line segment BA at A’ (see figure). Then, A’ BC’ is the required triangle.
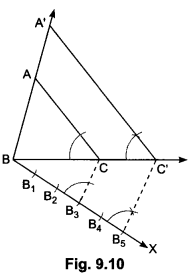
Justification:
Note that ∆ABC ~ ∆A’BC” (Since AC || A’C’)
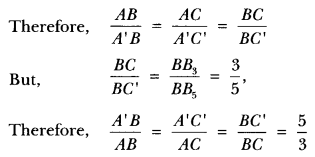
Question 2.
Draw a circle of radius of 3 cm. Take two points P and Q on one of its diameters extended on both sides, each at a distance of 7 cm on opposite sides of its centre. Draw tangents to the circle from these two points P and Q.
Solution:
Steps of Construction:
Step 1: Taking a point ( as centre, draw a circle of radius 3 cm.
Step II: Take two points P and Q on one of its extended diameter such that OP = OQ = 7 cm.
Step III: Bisect OP and OQ and let M1 and M2 be the mid-points of OP and OQ respectively.
Step IV: Draw a circle with M1 as centre and M1 P as radius to intersect the circle at T1, and T2.
Step V: Join PT1 and PT2.
Then, PT1 and PT2 are the required tangents. Similarly, the tangents QT3 and QT4 can be obtained
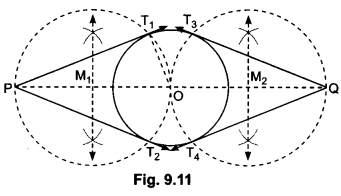
Justification:
On joining OT1, we find ∠PT1O = 90°, as it is an angle in the semicircle.
PT1 ⊥ OT1
Since OT1 is a radius of the given circle, so PT1 has to be a tangent to the circle.
Similarly, PT2, QT3 and QT4 are also tangents to the circle.
Question 3.
Let ABC be a right triangle in which AB = 6 cm, BC = 8 cm and ∠B = 90°. BD is the perpendicular from B on AC. The circle through B, C, D is drawn. Construct the tangents from A to this circle.
Solution:
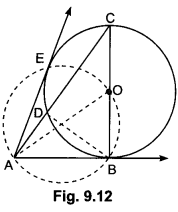
Steps of Construction:
Step I: Draw ∆ABC and perpendicular BD from B on AC.
Step II: Draw a circle with BC as a diameter. This circle will pass through D.
Step III: Let O be the mid-point of BC. Join A0.
Step IV: Draw a circle with AO as diameter. This circle cuts the circle drawn in step II at B and E.
Step V: Join AE. AE and AB are desired tangents drawn from A to the circle passing through B, C and D.
Question 4.
Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. Then construct another triangle whose sides are \(\frac{5}{3}\) times the corresponding sides of the given triangle.
Solution:
Steps of Construction:
Step I: Construct a SABC in which BC = 4 cm, ∠B = 90° and BA = 3 cm.
Step II: Below BC, make an acute ∠CBX.
Step III: Along BX mark off five arcs: B1, B2, B3, B4 and B5 such that
BB1 = B1B2 = B2B3 = B3B4 = B4B5.
Step IV: Join B3C.
Step V: From B5, draw B5D || B3C, meeting BC produced at D.
Step VI: From D, draw ED || AC, meeting BA produced at E. Then EBD is the required triangle whose sides are \(\frac{5}{3}\) times the corresponding sides of ∆ABC.
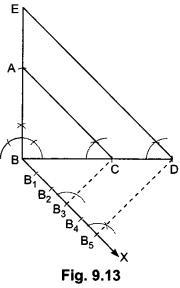
Justification:
Since, DE || CA
![]()
Hence, we have the new triangle similar to the given triangle whose sides are equal to \(\frac{5}{3}\) times the corresponding sides of ∆ABC.
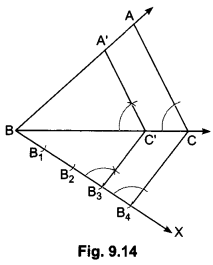
Question 5.
Construct a triangle similar to a given triangle ABC with its sides equal to \(\frac{3}{4}\) of the corresponding sides of the triangle ABC ( i.e., of scale factor \(\frac{3}{4}\)).
Solution:
Steps of Construction:
Step I: Draw any ray BX making an acute angle with BC on the side opposite to the vertex A.
Step II: Locate 4 arcs B1, B2, B3, and B4 on BX so that
BB1 = B1B2 = B2B3 = B3B4.
Step III: Join B4C and draw a line through B3 parallel to B4C to intersect BC at C’.
Step VI: Draw a line through C’ parallel to the line CA to intersect BA at A’ (Fig. 9.14).
Then, ∆A’ BC’ is the required triangle.
Let us now see how this construction gives the required triangle.
Justification:
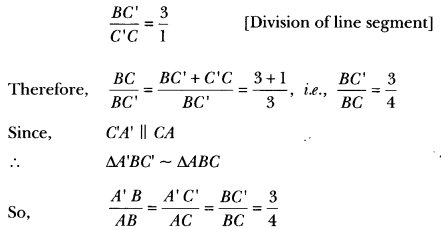
Question 6.
Draw a triangle ABC in which AB = 4 cm, BC = 6 cm and AC = 9 cm. Construct a triangle similar to ∆ABC with scale factor \(\frac{3}{2}\). Justify the construction. Are the two triangles congruent?
Note that all the three angles and two sides of the two triangles are equal.
Solution:
Steps of Construction:
Step I: Draw a line segment BC = 6 cm.
Step II: With centre B and radius 4 cm draw an arc.
Step III: With centre C and radius 9 cm draw another arc which intersects the previous arc at A.
Step IV: Join BA and CA. ABC is the required triangle.
Step V: Through B, draw an acute angle CBX on the side opposite to vertex A.
Step VI: Locate three arcs B1, B2, and B3 on BX such that BB1 = B1B2 = B2B3.
Step VII: Join B2C.
Step VIII: Draw B3C’ || B2C intersecting the extended line segment BC at ∠C’.
Step IX: Draw C’A’ || CA intersecting the extended line segment BA to A’.
Thus, ∆A’BC’ is the required triangle (∆A’BC’ ~ ∆ABC).
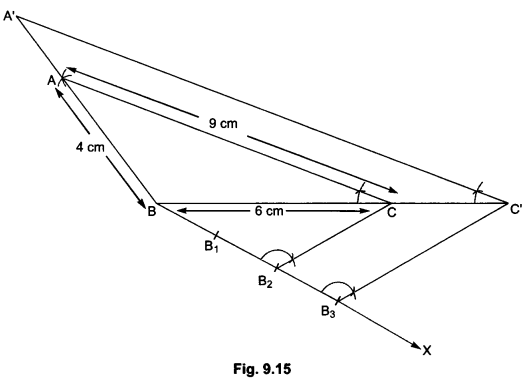
Justification:
∵ B2C || B3C’
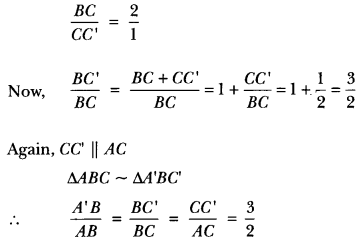
Constructions Class 10 Extra Questions HOTS
Question 1.
Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this point to the circle.
Solution:
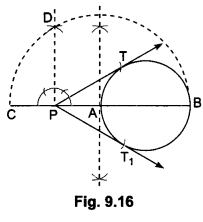
Steps of Construction:
Step I: Draw a circle with the help of a bangle.
Step II: Let P be the external point from where the tangents are to be drawn to the given circle. Through P, draw a secant PAB to intersect the circle at A and B (say).
Step III: Produce AP to a point C, such that AP = PC, i.e., P, is the mid-point of AC.
Step IV: Draw a semicircle with BC as diameter.
Step V: Draw PD ⊥ CB, intersecting the semicircle at D.
Step VI: With P as centre and PD as radius, draw arcs to intersect the given circle at T and T1.
Step VII: Join PT and PT1. Then, PT and PT1 are the required tangents.
Question 2.
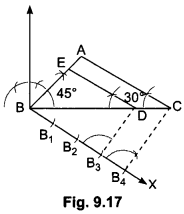
Draw a ∆ABC with side BC = 7 cm, ∠B = 45°, ∠A = 105°. Then, construct a triangle whose sides are \(\frac{3}{4}\) times the corresponding sides of ∆ABC.
Solution:
Steps of Construction:
Step 1: Construct a ∆ABC in which BC = 7 cm,
∠B = 45°, ∠C = 180° – (∠A + ∠B)
= 180° – (105° + 45°) = 180o – 150° = 30°.
Step II: Below BC, make an acute angle ∠CBX.
Step III: Along BX, mark off four arcs: B1, B2, B3, and B4 such that BB1 = B1B2 = B2B3 =B3B4.
Step IV: Join B4C
Step V: From B3, draw B3D || B4C meeting BC at D.
Step VI: From D, draw ED || AC, meeting BA at E. Then EBD is the required triangle whose sides are \(\frac{3}{4}\) times the corresponding sides of ∆ABC.
Justification:
![]()
Hence, we have the new triangle similar to the given triangle whose sides are equal to \(\frac{3}{4}\) times the corresponding sides of ∆ABC.
Question 3.
Draw a pair of tangents to a circle of radius 4 cm which are inclined to each other at an angle of 60°
OR
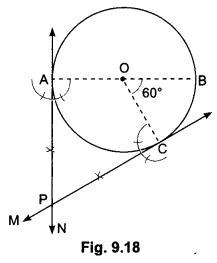
Draw a circle of radius 4 cm. Construct a pair of tangents to it, the angle between which is 60°. Also justify the construction. Measure the distance between the centre of the circle and the point of intersection of tangents.
Solution:
Steps of Construction:
Step I: Draw a circle with centre 0 and radius 4 cm.
Step II: Draw any diameter AOB.
Step III: Draw a radius OC such that ∠BOC = 60°.
Step IV: At C, we draw CM ⊥ OC and at A, we draw AN ⊥ OA.
Step V: Let the two perpendiculars intersect each other at P. Then, PA and PC are required tangents.
Justification:
Since OA is the radius, so PA has to be a tangent to the circle. Similarly, PC is also tangent to the circle.
∠APC = 360° – (∠OAP + ∠OCP + ∠AOC)
= 360° – (90° + 90° + 120°) = 360° – 300° = 60°
Hence, tangents PA and PC are inclined to each other at an angle of 60°