Here we are providing Class 12 Physics Important Extra Questions and Answers Chapter 13 Nuclei. Important Questions for Class 12 Physics with Answers are the best resource for students which helps in Class 12 board exams.
Class 12 Physics Chapter 13 Important Extra Questions Nuclei
Nuclei Important Extra Questions Very Short Answer Type
Question 1.
What will be the ratio of the radii of two nuclei of mass numbers A1 and A2?
Answer:
The ratio is \(\frac{R_{1}}{R_{2}}=\left(\frac{A_{1}}{A_{2}}\right)^{1 / 3}\)
Question 2.
Two nuclei have mass numbers in the ratio 1: 2. What is the ratio of their nuclear densities?
Answer:
The densities of both nuclei are equal as they do not depend upon mass number.
Question 3.
A nucleus of mass number A has a mass defect Δm. Give the formula, for the binding energy per nucleon of this nucleus.
Answer:
The formula is E = \(\frac{\Delta m \times c^{2}}{A}\)
Question 4.
Write the relation between half-life and decay constant of a radioactive sample.
The relation is T1/2 = \(\frac{0.693}{\lambda}\)
Question 5.
Write the nuclear decay process for β-decay of 1532P.
Answer:
The process is
![]()
Question 6.
State the relation between the mean life (τ) of a radioactive element and its decay constant λ.
Answer:
The two are related as τ = 1 / λ.
Question 7.
Write any two characteristic properties of nuclear force. (CBSE AI 2011)
Answer:
- Do not obey inverse square law and
- Spin-dependent.
Question 8.
How is the radius of a nucleus related to its mass number? (CBSE AI 2011C, AI 2013C)
Answer:
The radius R of the nucleus and mass number A is related as R = RoA1/3, where Ro is a constant.
Question 9.
A nucleus undergoes β – decay. How does
(i) the mass number,
(ii) atomic number change? (CBSE Delhi 2011C)
Answer:
During β – decay
(i) the mass number remains the same,
(ii) atomic number increases by one.
Question 10.
Define the activity of a given radioactive substance. Write its SI unit. (CBSE AI 2013)
Answer:
The rate of disintegration in a radioactive substance is known as its activity. SI unit is becquerel (Bq).
Question 11.
Why is it found experimentally difficult to detect neutrinos in nuclear β-decay? (CBSE AI 2014)
Answer:
They are very difficult to detect since they can penetrate a large quantity of matter (even earth) without any interaction.
Question 12.
Four nuclei of an element undergo fusion to form a heavier nucleus, with the release of energy. Which of the two — the parent or the daughter nucleus – would have higher binding energy per nucleon? (CBSE AI 2018, Delhi 2018)
Answer:
Daughter nucleus.
Question 13.
Why is nuclear fusion not possible In the laboratory?
Answer:
Because temperature as high as 107 K cannot be sustained in the laboratory.
Question 14.
Why is the penetrating power of gamma rays very large?
Answer:
Because they have high energy and are neutral.
Question 15.
Can it be concluded from beta decay that electrons exist inside the nucleus?
Answer:
No, the beta particle although an electron is actually created at the instant of beta decay and ejected at once. It cannot exist inside the nucleus as its de-Broglie wavelength is much larger than the dimensions of the nucleus.
Question 16.
Why is the ionizing power of α – parties greater than that of γ-rays?
Answer:
Because α – particles are heavy particles and their speed is comparatively small, so they collide more frequently with atoms of the medium and ionize them.
Question 17.
When a nucleus undergoes alpha decay, is the product atom electrically neutral in beta decay?
Answer:
No, in alpha decay, the atomic number decreases by 2 hence the atom is left with 2 extra orbital electrons. It, therefore, has a double negative charge. In beta decay, the atom is left with a net positive charge.
Question 18.
You are given two nuclides 37X and 34Y. Are they the isotopes of the same element? Why?
Answer:
Yes, because an atomic number of both nuclides is 3.
Question 19.
The variation of the decay rate of two radioactive samples A and B with time is shown in the figure. Which of the two has a greater decay constant? (NCERT Exemplar)
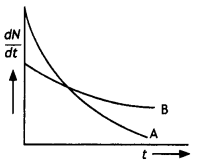
Answer:
The decay constant of A is greater than that of B but it does not always decay faster than B.
Question 20.
Does the ratio of neutrons to protons in a nucleus increase, decrease, or remain the same after the emission of an alpha particle? (NCERT Exemplar)
Answer:
The ratio of neutrons to protons in a nucleus increases after the emission of an alpha particle.
Question 21.
Which property of nuclear force explains the approximate constancy of binding energy per nucleon with mass number A for nuclei in the range 30 < A < 170? (CBSE2019C)
Answer:
The short-range nature of the nuclear force explains the approximate constancy of binding energy per nucleon with mass number A in the range 30 < A < 170.
Question 22.
Draw a graph showing the variation of decay rate with a number of active nuclei. (NCERT Exemplar)
Answer:
The graph is as shown.
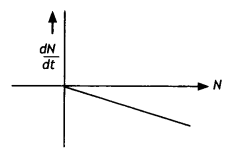
Question 23.
Which sample, A or B, shown in the figure has a shorter mean-life? (NCERT Exemplar)
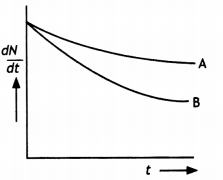
Answer:
B has shorter mean life as λ is greater forB.
Question 24.
Why do stable nuclei never have more protons than neutrons? (NCERT Exemplar)
Answer:
Protons are positively charged and repel one another electrically. This repulsion becomes so great in nuclei with more than 10 protons or so that an excess of neutrons, which produce only attractive forces, is required for stability.
Question 25.
Why does the process of spontaneous nuclear fission occur in heavy nuclei? (CBSE 2019C)
Answer:
Because heavy nuclei contain a large number of protons that exert strong repulsive forces on one another.
Nuclei Important Extra Questions Short Answer Type
Question 1.
Draw the curve showing the binding energy/nucleon with a mass number of different nuclei. Briefly state, how nuclear fusion and nuclear fission can be explained on the basis of this graph.
Answer:
The diagram is as shown.
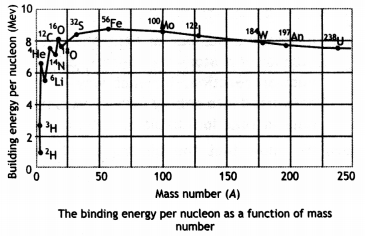
Light nuclei have a small value of binding energy per nucleon, therefore to become more stable they fuse to increase their binding energy per nucleon.
A very heavy nucleus, say A 240, has Lower binding energy per nucLeon compared to that of a nucleus with A = 120. Thus if a nucleus A = 240 breaks into two A = 120 nuclei, nucleons get more tightLy bound. This implies energy would be released in the process.
Question 2.
Define decay constant for a radioactive sample. Which of the following radiations α, β, and γ rays
(i) are similar to X-rays,
(ii) are easily absorbed by matter, and
(iii) are similar in nature to cathode rays?
Answer:
The decay constant is defined as the reciprocal of that time duration for which the number of nuclei of the radioactive sample decays to 1 / e or 37 % of its original value.
(i) Gamma
(ii) Alpha
(iii) Beta
Question 3.
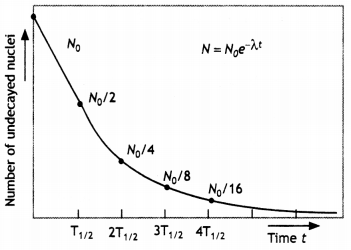
State the law of radioactive decay.
Plot a graph showing the number of undecayed nuclei as a function of time (t) for a given radioactive sample having a half-life T1/2.
Depict In the plot the number of undecayed nuclei at (i) t = 3T1/2 and (ii) t = 5 T1/2 (CBSE Delhi 2011)
Answer:
The number of nuclei disintegrating per second is proportional to the number of nuclei present at the time of disintegration and is independent of alt physical conditions like temperature, pressure, humidity, chemical composition, etc.
The plot is as shown.
Question 4.
Draw a plot of the potential energy of a pair of nucleons as a function of their separations. Mark the regions where the nuclear force is (i) attractive and (ii) repulsive. Write any two characteristic features of nuclear forces. (CBSE AI 2012)
Answer:
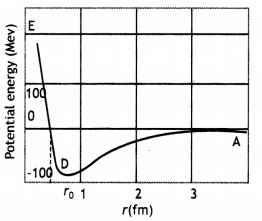
For r > r0 (attraction), For r < ro (repulsion)
- Strong attractive force (stronger than the repulsive electric force between the protons)
- Are short-range forces.
Question 5.
(a) Write the relation for binding energy (BE) (in MeV) of a nucleus of mass ZAM atomic number (Z) and mass number (A) in terms of the masses of its constituents – neutrons and protons.
Answer:
The required expression is
ΔE = (Zmp + (A – Z)mn – M) × 931 MeV
(b) Draw a plot of BE/A versus mass number A for 2 ≤ A ≤ 170. Use this graph to explain the release of energy in the process of nuclear fusion of two light nuclei. (CBSE Delhi 2014C)
Answer:
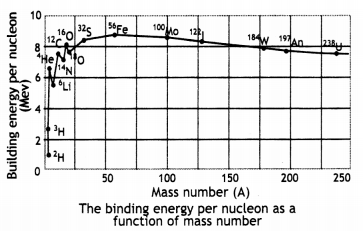
Since the binding energy of the smaller nuclei like hydrogen is less, therefore they fuse together to form helium in order to increase their binding energy per nucleon and become stable. This means that the final system is more tightly bound than the initial system. Again energy would be released in such a process of fusion.
Question 6.
If both the number of neutrons and the number of protons are conserved in each nuclear reaction, in what way is mass converted into energy (or vice versa) in a nuclear reaction? Explain. (CBSE AI2016C)
Answer:
We know that the binding energy of a nucleus gives a negative contribution to the mass of the nucleus (mass defect). Now, since proton number and neutron number are conserved in a nuclear reaction the total rest mass of neutrons and protons is the same on either side of a reaction. But the total binding energy of nuclei on the left side need not be the same as that on the right-hand side.
The difference in these binding energies appears as the energy released or absorbed in a nuclear reaction. Since binding energy contributes to mass, we say that the difference in the total mass of nuclei on the two sides gets converted into energy or vice-versa.
Question 7.
State two properties of nuclear forces. Write the relation between half-life and decay constant of a radioactive nucleus. (CBSE AI 2017C)
Answer:
- They are saturated forces.
- They are charge-independent.
The required relation is
T = \(\frac{\ln 2}{\lambda}=\frac{2.303 \log 2}{\lambda}=\frac{0.693}{\lambda}\)
Question 8.
(a) Draw a graph showing the variation of binding energy per nucleon (BE/A) vs mass number A for the nuclei in 20 ≤ A ≤ 170.
Answer:

Since the binding energy of the smaller nuclei like hydrogen is less, therefore they fuse together to form helium in order to increase their binding energy per nucleon and become stable. This means that the final system is more tightly bound than the initial system. Again energy would be released in such a process of fusion.
(b) A nucleus of mass number 240 and having binding energy/nucleon 7.6 MeV splits into two fragments Y, 1 of mass numbers 110 and 130 respectively. If the binding energy/ nucleon of Y, 1 is equal to 8.5 MeV each, calculate the energy released in the nuclear reaction. (CBSE Al 2017C)
Answer:
Energy released per fission
= (110 + 130) × 8.5 – 240 × 7.6
= 240 × (8.5 – 7.6) MeV
= 240 × 0.9
= 216.0 MeV
Question 9.
Explain with the help of an example, whether the neutron-proton ratio in a nucleus increases or decreases due to beta decay.
Answer:
Consider the following decay
![]()
Number of neutrons before beta decay
= 234-90 = 144
Number of neutrons after beta decay
= 234-91 =143
Number of protons before beta decay
= 90
Number of protons after beta decay
= 91
Neutron-proton ratio before beta decay
= \(\frac{144}{90}\) = 1.6
Neutron-proton ratio after beta decay
= \(\frac{143}{91}\) = 1.57
Thus neutron-proton ratio decreases during beta decay.
Question 10.
How is the size of a nucleus experimentally determined? Write the relation between the radius and mass number of the nucleus. Show that the density of the nucleus is independent of its mass number. (CBSE Delhi 2011C)
Answer:
The size of the nucleus can be determined by the Rutherford experiments on alpha particles scattering. The distance of the nearest approach is approximately the size of the nucleus. Here it is assumed that only coulomb repulsive force caused scattering. With alpha rays of 5.5 MeV, the size of the nucleus was found to be less than 4 × 10-14 m. By doing scattering experiments with fast electrons bombarding targets of different elements, the size of the nuclei of various elements determined accurately.
The required relation is
R = RoA1/3, where Ro = 1.2 × 10-15 m
The density of a nucleus of mass number A and radius R is given by
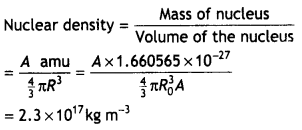
which is independent of the mass number A.
Question 11.
(a) What characteristic property of nuclear force explains the constancy of binding energy per nucleon (BE/A) in the range of mass number ‘A’ lying 30 < A < 170?
Answer:
The nuclear force between two nucleons falls rapidly to zero as their distance is more than a few femtometres. This leads to the saturation of forces in a medium or a large-sized nucleus, i.e. nuclei for which A is 30 < A < 170, which is the reason for the constancy of the binding energy per nucleon.
(b) Show that the density of nucleus over a wide range of nuclei is constant- independent of mass number A. (CBSE AI 2012)
Answer:
The size of the nucleus can be determined by the Rutherford experiments on alpha particles scattering. The distance of the nearest approach is approximately the size of the nucleus. Here it is assumed that only coulomb repulsive force caused scattering. With alpha rays of 5.5 MeV, the size of the nucleus was found to be less than 4 x 10-14 m. By doing scattering experiments with fast electrons bombarding targets of different elements, the size of the nuclei of various elements determined accurately.
The required relation is
R = RoA1/3, where Ro = 1.2 × 10-15 m
The density of a nucleus of mass number A and radius R is given by
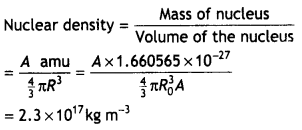
which is independent of the mass number A.
Question 12.
A radioactive nucleus ‘A’ decays as given below:
![]() .
.
If the mass number and atomic number of A1 are 180 and 73 respectively, find the mass number and an atomic number of A and A2.
Answer:
For A : Z = 72 and A = 180
For A2: Z = 71 and A = 176
Question 13.
The sequence of stepwise decay of a radioactive nucleus is![]() . If the nucleon number and atomic number for D2 are 176 and 71 respectively, what are the corresponding values of D and D3? Justify your answer in each case.
. If the nucleon number and atomic number for D2 are 176 and 71 respectively, what are the corresponding values of D and D3? Justify your answer in each case.
Answer:
For D: A = 180, Z = 72
For D3: A = 172, Z = 69
During alpha decay mass number decreases by 4 and the atomic number decreases by 2, while during beta decay the mass number remains the same, and the atomic number increases by 1.
Question 14.
Write symbolically the nuclear β+ decay process of 611C. Is the decayed product X an isotope or isobar of611C?
Given the mass values m (611C) = 11.011434 u and m (X) = 11.009305 u. (CBSE AI 2015)
Estimate the Q – value in this process.
Answer:
The required equation is
![]()
X is an isobar
Mass defect = m(C) – m(X)
= (11.011434- 11.009305) u = 0.002129 u
Therefore Q = Δm × 931.5 MeV
= 0.002129 × 931.5 = 1.98 MeV
Question 15.
Two radioactive samples, X, Y have the same number of atoms at t = 0. Their half¬lives are 3 h and 4 h respectively. Compare the rates of disintegration of the two nuclei after 12 hours. (CBSE AI 2017C)
Answer:
Let N0 be the nuclei present in X and Y at t = 0. Given Tx = 3 h and Ty = 4 h, t = 12 h.
The number of nuclei present in X and Y after 12 hours is
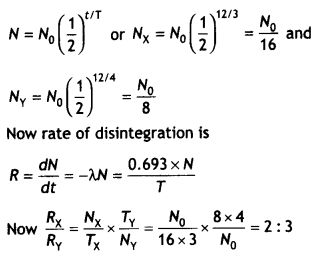
Question 16.
A radioactive sample has the activity of 10,000 disintegrations per second after 20 hours. After the next 10 hours, its activity reduces to 5,000 dis. sec-1. Find out its half-life and initial activity. (CBSE Delhi 2017C)
Answer:
Since activity reduces to half in 10 hours from 10000 dis. sec-1 to 5000 dis. sec-1, therefore half-life of the sample will be 10 years.
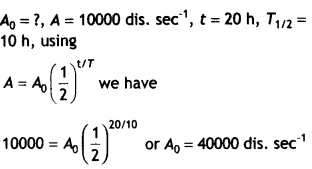
Question 17.
Why is the energy of the beta particles emitted during beta decay continuous?
Answer:
The phenomenon of beta decay arises due to the conversion of a neutron in the nucleus into a proton, electron, and an anti-neutrino. Because the energy available in beta decay is shared by the electron and the anti-neutrino in all possible ratios as they come out of the nucleus, therefore the beta ray energy spectrum is continuous in nature.
Question 18.
Explain, how radioactive nuclei can emit β-particles even though atomic nuclei do not contain these particles. Hence explain why the mass number of a radioactive nuclide does not change during β-decay.
Answer:
Beta-particles (or electrons) as such are not present inside a nucleus. However, in the case of a radioactive nuclide, sometimes a neutron decays into a proton, an electron, and an antineutrino as given by the following equation:
![]()
where mass and charge of antineutrino particle is zero. Out of the particles formed, the proton remains within the nucleus itself but electron along with antineutrino comes out of the nucleus. It is this electron that is being emitted as a beta-particle.
As in the process of β-emission, one proton is produced in the nucleus at the expense of a neutron and the mass number of both is the same, hence the mass number of the nuclide remains unchanged during p-decay.
Question 19.
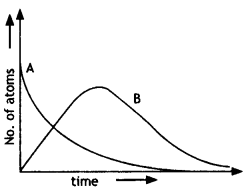
Consider a radioactive nucleus A which decays to a stable nucleus C through the following sequence: A → B → C. Here B is an intermediate nucleus that is also radioactive. Considering that there are No atoms of A initially, plot the graph showing the variation of the number of atoms of A and B versus time. (NCERT Exemplar)
Answer:
At t = 0, NA = No while NB = 0. As time increases, NA falls off exponentially, while the number of atoms of B increases, becomes maximum, and finally decays to zero ∞ (following exponential decay law).
Hence the graph is as shown.
Nuclei Important Extra Questions Long Answer Type
Question 1.
Define the terms: half-life period and decay constant of a radioactive sample. Derive the relation between these terms.
Answer:
The half-life is the time required for the number of radioactive nuclei to decrease to one-half the original number.
The decay constant is defined as the reciprocal of that time duration for which the number of nuclei of the radioactive sample decays to 1 / e or 37% of its original value.
To get the relation for half life T and decay constant λ we set N = \(\frac{N_{0}}{2}\) and t = T in the equation N = No e-λt, obtaining \(\frac{1}{2}\) = e-λt
Taking the logarithm of both sides and solving for T we have
T = \(\frac{\ln 2}{\lambda}=\frac{2.303 \log 2}{\lambda}=\frac{0.693}{\lambda}\)
Question 2.
(a) Draw a graph showing the variation of the potential energy of a pair of nucleons as a function of their separation. Indicate the regions in which nuclear force is (i) attractive, and (ii) repulsive.
Answer:
Graph showing the variation of potential energy U (in MeV) of a pair of nucleons as a function of their separation r (in fm) is shown here.
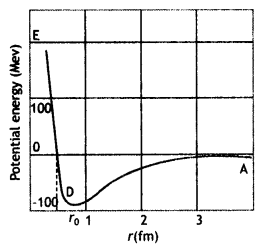
- In the graph region AD (r > ro) shows the region where nuclear force is strongly attractive.
- The region DE (r < ro) shows the region where nuclear force is strongly repulsive.
(b) Write two characteristic features of nuclear force which distinguish it from the Coulomb force.
Answer:
Two characteristics of nuclear forces which distinguish it from Coulomb’s force are
- It is charge Independent.
- It is an extremely short-range force and does not obey the inverse square law.
Question 3.
Prove that the Instantaneous rate of change of the activity of a radioactive substance is Inversely proportional to the square of Its half-life.
Answer:
The activity of a radioactive substance is
A = \(\frac{dN}{dt}\).
We know that the number of nuclei of a radioactive substance Left behind after time t is given by N = Noe-λt
Differentiating the above relation with respect to time we have
A = \(\frac{d N}{d t}=\frac{d}{d t}\)Noe-λt = – Noλe-λt
Differentiating the above equation with respect to time we have
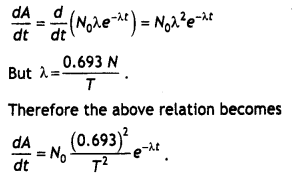
Therefore the Instantaneous rate of change of the activity of a radioactive substance is inversely proportional to the square of Its half Life.
Question 4.
(a) Deduce the expression N = Noe-λt the law of radioactive decay.
(b) (i) Write symbolically the process expressing the β+ decay of, 1122Na Also write the basic nuclear process underlying this decay.
(ii) Is the nucleus formed in the decay of the nucleus 1122Na an Isotope or isobar? (CBSE Delhi 2014)
Answer:
(a) Let N0 be the number of nuclei present in a freshly separated sample of a radioactive substance. Let after time t the number of nuclei left behind be N. Let dN number of nuclei disintegrate in a small time interval dt. Then by the – decay law,
where λ is a constant of proportionality.
Question 5.
(a) Complete the following nuclear reactions:
Answer:
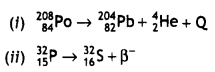
(b) Write the basic process Involved in nuclei responsible for (i) β– and (ii) β+ decay.
Answer:
The basic nuclear process underlying β– decay is the conversion of the neutron to proton
n → p + e– + v–
while for v+ decay, it is the conversion of a proton into a neutron
p → n + e+ + v
(c) Why is it found experimentally difficult to detect neutrinos? (CBSE AI 2015 C)
Answer:
Neutrinos are neutral particles with very small (possibly, even zero) mass compared to electrons. They have only weak interaction with other particles. They are, therefore, very difficult to detect, since they can penetrate a large quantity of matter (even earth) without any interaction.
Question 6.
(a) Explain the processes of nuclear fission and nuclear fusion by using the plot of binding energy per nucleon (B.E./A) versus the mass number A.
Answer:
For the graph

From the plot, we note that
- During nuclear fission: A heavy nucleus in the larger mass region (A > 200) breaks into two middle-level nuclei, resulting in an increase in B.E./ nucleon. This results in the release of energy,
- During nuclear fusion: Light nuclei in the lower mass region (A < 20) fuse to form a nucleus having higher B.E. / nucleon. Hence Energy gets released.
(b) A radioactive Isotope has a half-life of 10 years. How long will It take for the activity to reduce to 3.125%? (CBSE AI2018)
Answer;
3.125% means that the number of nuclei decays to 1/32 of its original value.
Therefore,
\(\frac{N}{N_{0}}=\frac{1}{32}=\left(\frac{1}{2}\right)^{5}\)
Now we know that
N = N0\(\left(\frac{1}{2}\right)^{t / T}\)
Therefore we have
\(\left(\frac{1}{2}\right)^{5}=\left(\frac{1}{2}\right)^{t / T}\)
Therefore
t = 5T = 5 × 10 = 50 years
Question 7.
Group the following six nuclides into three pairs of (?) isotones, (ii) isotopes, and (iii) isobars: 612C, 23He, 80198Hg, 13H, 79197Au 614C. How does the size of the nucleus depend on its mass number? Hence explain why the density of nuclear matter should be independent of the size of the nucleus.
Answer:
(a) Isotones: 80198Hg, 79197Au
(6) Isotopes: 612C , 614C
(c) Isobars: 23He, 13H
The size of a nucleus depends upon its mass number as R = R0 A1/3
The nuclear density is given by the expression
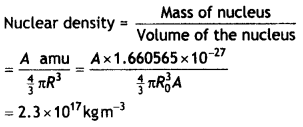
The calculations show that the nuclear density is independent of the mass number.
Question 8.
Define the term ‘decay constant’ of a radioactive sample. The rate of disintegration of a given radioactive nucleus is 10,000 disintegrations/s and 5,000 disintegration/s after 20 hr and 30 hr respectively from start. Calculate the half-life and an initial number of nuclei at t = 0. (CBSE Delhi 2019)
Answer:
The decay constant of a radioactive element is the reciprocal of the time in which the number of its nuclei reduces to 1 /e of its original number.
We have R = λN
R(20hrs) = 100o0 = λN20
R(30hrs) = 5000 = λN30
\(\frac{N_{20}}{N_{30}}\) = 2
This means that the number of nuclei, of the given radioactive nucleus, gets halved in a time of (30 – 20) hours = 10 hours
Half-life = 10 hours
This means that in 20 hours (= 2 half-Lives), the original number of nuclei must have gone down by a factor of 4.
Hence rate of decay at t = 0
λ N0 = 4 λ N20
R0 = 4 × 10,000 = 40,000 disintegration per second
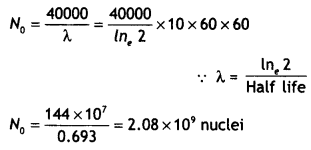
Question 9.
(a) Write the relation between half-life and an average life of a radioactive nucleus.
Answer:
The relation is τ = 1 .44T1/2
(b) In a given sample two isotopes A and B are initially present in the ratio of 1:2. Their half-lives are 60 years and 30 years respectively. How long will it take so that the sample has these isotopes in the ratio of 2:1? (CBSE Delhi 2019)
Answer:
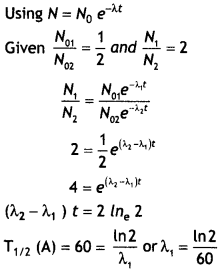
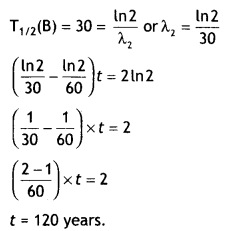
Question 10.
Distinguish between nuclear fission and fusion. Show how in both these processes energy is released. Calculate the energy release in MeV in the deuterium-tritium fusion reaction:
![]()
Using the data m(21H) = 2.014102 u,
m(13H) = 3.016949u, m(24He) = 4.002603 u,
mn = 1.008665 u,1 u = 931.5 MeV/c2 (CBSE Delhi 2015)
Answer:
The distinction is shown in the table below.
| Nuclear Fission | Nuclear Fusion |
| 1. It is the splitting of a heavy nucleus into two or tighter unstable nuclei. | 1. It is the combining of two light nuclei into a heavier nucleus. |
| 2. It may or may not be a chain reaction. | 2. It is always a chain reaction. |
| 3. It is independent of temperature. | 3. It is temperature-dependent. |
| 4. It can be controlled. | 4. It can’t be controlled. |
| 5. Tremendous amount of energy is released. | 5. Energy released per unit mass is seven times the energy released during fission. |
| 6. By-products are harmful. | 6. By-products are not harmful. |
| 7. Example of reaction – The atom bomb. | 7. Example of reaction – Reaction in stars, hydrogen born |
In both reactions, there is a mass defect that is converted into energy.
Now energy released in the reaction

Question 11.
(a) Draw a plot showing the variation of the potential energy of a pair of nucleons as a function of their separation. Mark the regions where the nuclear force is (a) attractive and (b) repulsive.
Answer:
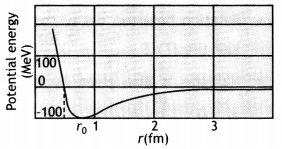
For r > ro, the force is attractive For r < ro, the force is repulsive
(b) In the nuclear reaction
![]()
determine the values of a and b. (CBSE Delhi 2018 C)
Answer:
We have,
1 + 235 = a + 94 + 2 × 1
∴ a = 236 – 96 = 140
Also
0 + 92 = 54+ 6 + 2 × 0
∴ b = 92 – 54 = 38
Question 12.
Binding energy per nucleon versus mass number curve is as shown. ZAS, Z1A1w, Z2A2X, and Z3A3Y, are four nuclei indicated on the curve.
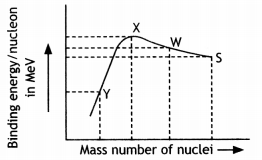
Based on the graph:
(а) Arrange X, W, and S in the increasing order of stability.
Answer:
(a) S, W, and X
(b) Write the relation between the relevant A and Z values for the following nuclear reaction. S → X + W
Answer:
The equation is![]()
Z = Z1 + Z2 and A = A1 + A2
(c) Explain why binding energy for heavy nuclei is low. (CBSE Sample Paper 2018-19)
Answer:
Reason for low binding energy: For heavier nuclei, the Coulomb repulsive force between protons increases considerably and offsets the attractive effects of the nuclear forces. This can result in such nuclei being unstable.
Question 13.
(a) Derive the law of radioactive decay,
viz. N = Noe-λt
Answer:
Let N0 be the number of nuclei present in a freshly separated sample of a radioactive substance. Let after time t the number of nuclei left behind be N. Let dN number of nuclei disintegrate in a small time interval dt. Then by the – decay law,
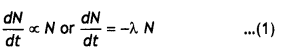
where λ is a constant of proportionality.
(b) Explain, giving necessary reactions, how energy is released during
(i) fission
Answer:
Nuclear Fission: It is a process in which a heavy nucleus splits up into two Lighter nucLei of nearly equal masses. It is found that the sum of the masses of the product nuclei and particles is less than the sum of the masses of the reactants, i.e. there is some mass defect. This mass defect appears as energy. One such fission reaction is given below:
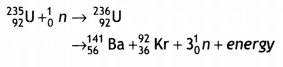
The Q value of the above reaction is about 200 MeV. The sum of the masses of Ba, Kr, and 3 neutrons is less than the sum of the masses of U and one neutron.
(ii) fusion
Nuclear Fusion: It is the process in which two light nuclei combine together to form a heavy nucleus. For fusion very high temperature of l is required. One such fusion reaction is given below:
![]()
The Q value of this nuclear reaction is 24 MeV. It is the energy equivalent of the mass defect in the above reaction. The energy released in fusion is much less than in fission but the energy released per unit mass infusion is much greater than that released in fission.
Question 14.
(a) Distinguish between isotopes and isobars, giving one example for each.
(b) Why is the mass of a nucleus always less than the sum of the masses of its constituents? Write one example to justify your answer.
Or
(a) Classify the following six nuclides into (i) isotones, (ii) Isotopes, and (iii) isobars: (CBSEAI2019)
![]()
(b) How does the size of a nucleus depend on its mass number? Hence explain why the density of nuclear matter should be independent of the size of the nucleus.
Answer:
(a) Isotopes have the same atomic number while isobars have the same mass number
Examples of isotopes 612C, 614C
Examples of isobars 23He, 13H
(b) Mass of a nucleus is less than its constituents because in the bound state some mass is converted into binding energy which is energy equivalent of mass defect e.g., the mass of 1860 nucleus is less than the sum of masses of 8 protons and 8 neutrons
Or
(a) Isotones: 80198Hg, 79197Au
(6) Isotopes: 612C , 614C
(c) Isobars: 23He, 13H
(b) The radius of the nucleus is given by
R = RoA1/3
Volume of the nucleus \(\frac{4}{3}\)πR3 = \(\frac{4}{3}\)πRo3 A
If m is the average mass of the nucleon then the mass of the nucleus M = mA
Hence nuclear density
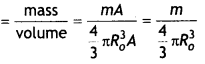
Which is independent of the A i.e., the size of the nucleus.
Numerical Problems:
- Radius of the nucleus R = RoA1/3
- Mass defect, Δm = Z mp + (A – Z) mn– M
- Energy released ΔE = Δm × 931 MeV
or
ΔE = [Z mp + (A – Z) mn – M] × 931 MeV - Binding energy per nucleon BE/N = ΔE/A
- Relation between original nuclei (N) and nuclei left (No) after time t N = Noe-λt
- Relation between decay constant (λ) and half-life (T) = \(\frac{\ln 2}{\lambda}=\frac{2.303 \log 2}{\lambda}=\frac{0.693}{\lambda}\)
- Half-life is also given by the expression N = No\(\left(\frac{1}{2}\right)^{n}\) where n = t/T
- The average life is given by
τ = \(\frac{1}{\lambda}=\frac{T}{\ln 2}=\frac{T}{0.693}\) = 1.44 T - Activity is given by A = -λN = \(\frac{0.693N}{T}\)
Question 1.
Calculate the binding energy per nucleon of Fe5626 Given mFe = 55.934939 u, mn = 1.008665 u and mp = 1.007825 u
Answer:
Number of protons Z = 26
Number of neutrons (A – Z) = 30
Now mass defect is given by
Δm = Z mp + (A – Z)mn – M
Δm = 26 × 1.007825 + 30 × 1.008665 – 55.934939
= 0.528461 u
Therefore binding energy
BE = Δm × 931 MeV = 0.528461 × 931
= 491.99 MeV
BE/nucleon = 491.99/56 = 8.785 MeV
Question 2.
The activity of a radioactive element drops to one-sixteenth of its initial value in 32 years. Find the mean life of the sample.
Answer:
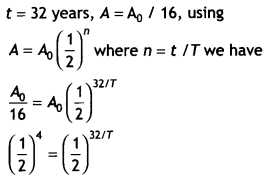
Or
32/T = 4 or 7 = 32 / 4 = 8 years.
Therefore mean life of the sample is τ = 1.44 7 = 1.44 × 8 = 11.52 years.
Question 3.
A radioactive sample contains 2.2 mg of pure 116C which has a half-life period of 1224 seconds. Calculate (i) the number of atoms present initially and (ii) the activity when 5 pg of the sample will be left.
Answer:
Mass of sample = 2.2 pg
Now 11 g of the sample contains 6.023 × 1023 nuclei, therefore the number of nuclei in 2.2 mg = 2.2 × 10-3 g are
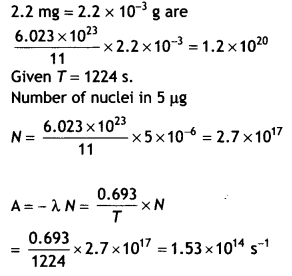
Question 4.
The half-life of 238 92U is 4.5 × 109 years. Calculate the activity of 1 g sample of 92238U.
Answer:
Given T = 4.5 × 109 years.
Number of nuclei of U in 1 g
= N = \(\frac{6.023 \times 10^{23}}{238}\) = 2.5 × 1021
Therefore activity
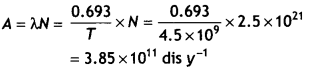
Question 5.
The decay constant for a given radioactive sample is 0.3456 per day. What percentage of this sample will get decayed in a period of 4 days?
Answer:
Given λ = 0.3456 day-1
or
T1/2 = 0.693/λ = 0. 693/ 0.3456 = 2.894 days, t = 4 days.
Let N be the mass left behind, then N = Noe-λt
or
N = No e-0 3456 × 4
or
N = N0 e-1 3824 = No × 0.25
Therefore the percentage of undecayed is
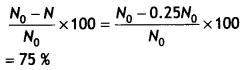
Question 6.
It is observed that only 6.25 % of a given radioactive sample is left undecayed after a period of 16 days. What is the decay constant of this sample per day?
Answer:
Given N/No = 6.25 %, t = 16 days, λ = ?
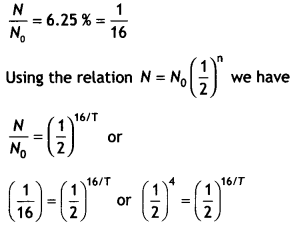
Or
16/ T = 4 or T = 4 days.
Therefore λ = 1/T = 1/4 = 0.25 day-1
Question 7.
A radioactive substance decays to 1/32th of its initial value in 25 days. Calculate its half-life.
Answer:
Given t = 25 days, N = No / 32, using
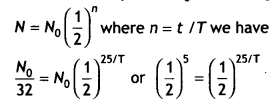
Or
25/7= 5 or T= 25 / 5 = 5 days.
Question 8.
The half-life of a radioactive sample is 30 s.
Calculate
(i) the decay constant, and
Answer:
Given T1/2 = 30 s, N = 3No / 4, λ = ?, t = ?
(i) Decay constant
λ = \(\frac{0.693}{T_{1 / 2}}=\frac{0.693}{30}\) = 0.0231 s-1
(ii) time taken for the sample to decay to 3/4 th of its initial value.
Answer:
Using N = Noe-λt we have
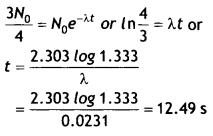
Question 9.
The half-life of 14 6C is 5700 years. What does it mean?
Two radioactive nuclei X and Y initially contain an equal number of atoms. Their half-lives are 1 hour and 2 hours respectively. Calculate the ratio of their rates of disintegration after 2 hours.
Answer:
It means that in 5700 years the number of nuclei of carbon decay to half their original value.
Given Nox = NoY, TX = 1 h, TY = 2 h, therefore
\(\frac{\lambda_{X}}{\lambda_{Y}}=\frac{2}{1}\) = 2
Now after 2 hours X will reduce to one- fourth and Y will reduce to half their original value.
If activities at t = 2 h are Rx and Ry respectively, then
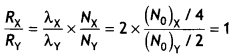
Thus their rate of disintegration after 2 hours is the same.
Question 10.
A star converts all its hydrogen to helium achieving 100% helium composition. It then converts helium to carbon via the reaction.
![]()
The mass of the star is 5 × 1032 kg and it generates energy at the rate of 5 × 1030 watt. How long will it take to convert all the helium to carbon at this rate?
As 4 × 10-3 kg of He consists of 6.023 × 1023 He nuclei so 5 × 1032 kg He will contain
\(\frac{6.023 \times 10^{23} \times 5 \times 10^{32}}{4 \times 10^{-3}}\) = 7.5 × 1058 nuclei
Now three nuclei of helium produce 7.27 × 1.6 × 10-13 J of energy
So all nuclei in the star will produce
E = \(\frac{7.27 \times 1.6 \times 10^{-13}}{3}\) × 7.5 × 1058
= 2.9 × 1046 J
As power generated is P = 5 × 1030 W, therefore time taken to convert all He nuclei into carbon is
t = \(\frac{E}{P}=\frac{2.9 \times 10^{46}}{5 \times 10^{30}}\) = 5.84 × 1015 s
or
1.85 × 108 years
Question 11.
Radioactive material is reduced to (1/16)th of its original amount in 4 days. How much material should one begin with so that 4 × 10-3 kg of the material is left after 6 days?
Answer:
N = No / 16, t = 4 days,
N = 4 × 10-3 kg,
t = 6 days
To calculate half-life of the material we have
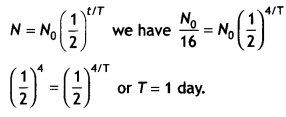
Now using the expression 4 × 10-3 = No\(\left(\frac{1}{2}\right)^{6 / 1}\)
Solving we have No = 0.256 kg
Question 12.
Two different radioactive elements with half-lives T1 and T2 have N1 and N2 (undecayed) atoms respectively present at a given instant. Determine the ratio of their activities at this instant.
Answer:
The activity of a radioactive sample is given by the relation
A = – λN
Therefore the ratio of activity of these two radioactive elements is
\(\frac{A_{1}}{A_{2}}=\frac{-\lambda_{1} N_{1}}{-\lambda_{2} N_{2}}=\frac{T_{2} N_{1}}{T_{1} N_{2}}\)
Question 13.
Given the mass of the iron nucleus as 55.85 u and A = 56. Find the nuclear density? (NCERT)
Answer:
Given mFe = 55.85 u = 9.27 × 10-26kg
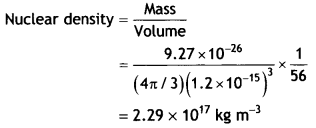
The density of matter in neutron stars (an astrophysical object) is comparable to this density. This shows that matter in these Neutron stars has been compressed to such an extent that they resemble a big nucleus.
Question 14.
We are given the following atomic masses: 92238U = 238.05079 u, 24He = 4.00260 u, 90234Th = 234.04363 u 11H = 1.00783 u, 91237Pa =237.05121 u Here the symbol Pa is for the element protactinium (Z = 91). (a) Calculate the energy released during the alpha decay of 92238U. (b) Show that cannot spontaneously emit a proton. (NCERT)
Answer:
(i) The alpha decay of 92238Uis given by
![]()
The energy released in this process is given by
Q= (Mu – MTh – MHe) × 931.5 MeV
Substituting the atomic masses as given in the data we find that
Q = (238.05079 – 234.04363 – 4.00260) × 931.5 MeV ⇒ Q = 4.25 MeV.
(ii) If 29®U spontaneously emits a proton, the decay process would be
![]()
The Q for this process to happen is Q = (Mu – Mpa – MH) × 931.5 MeV
Q = (238.05079 – 237.05121 – 1.00783) × 931.5 MeV ⇒ Q = – 7.68 MeV
Thus the Q of the process is negative and therefore it cannot proceed spontaneously. We will have to supply energy of 7.68 MeV to the 92238U nucleus to make it emit a proton.
Question 15.
The half-life of 90Sr is 28 years. What is the disintegration rate of 15 mg of this isotope? (NCERT)
Answer:
Given T1/2 = 28 years, m = 15 mg
Now the rate of disintegration is given by
