Here we are providing Class 11 Physics Important Extra Questions and Answers Chapter 9 Mechanical Properties of Solids. Important Questions for Class 11 Physics with Answers are the best resource for students which helps in Class 11 board exams.
Class 11 Physics Chapter 9 Important Extra Questions Mechanical Properties of Solids
Mechanical Properties of Solids Important Extra Questions Very Short Answer Type
Question 1.
Give an example of pure shear.
Answer:
The twisting of a cylinder produces pure shear.
Question 2.
What is an elastomer?
Answer:
It is a substance that can be elastically stretched to large values t of strain.
Question 3.
What is breaking stress?
Answer:
It is defined as the ratio of maximum load to which the wire is < subjected to the original cross-sectional area.
Question 4.
What is the:
(a) value of modulus of rigidity of a liquid?
Answer:
zero.
(b) order of strain within the elastic limit?
Answer:
10-3 cm per cm = 10-3 cm/cm.
Question 5.
A wire is stretched to double its length. What is the value of longitudinal strain?
Answer:
Unity.
Question 6.
Mention a situation where the restoring force is not equal and opposite to the applied force.
Answer:
This happens when the body is deformed beyond the elastic limit.
Question 7.
What is a Cantilever?
Answer:
It is a beam loaded at one end and free at the other end.
Question 8.
A wire is suspended from a roof but no weight is attached to the wire. Is the wire under stress?
Answer:
Yes, the weight of the wire itself acts as the deforming force.
Question 9.
Why strain has no units?
Answer:
As it is the ratio of two similar quantities.
Question 10.
What is Poisson’s ratio?
Answer:
It is the ratio of lateral strain to linear strain.
Question 11.
What is the:
(a) the bulk modulus of a perfectly rigid body?
Answer:
infinite.
(b) value of Y for a perfectly rigid body?
Answer:
infinite.
(c) bulk modulus for an incompressible liquid?
Answer:
infinite.
Question 12.
Why does spring balance shows wrong readings after they have been used for a long time?
Answer:
Because of elastic fatigue.
Question 13.
Name three physical properties which can have different values in different directions.
Answer:
Thermal conductivity, compressibility, and electrical conductivity.
Question 14.
What will happen to the potential energy if a wire is
(a) compressed,
(b) stretched?
Answer:
In both cases, the potential energy of the wire increases as work has to be done on the wire.
Question 15.
Which of the two materials (see figure here) would you choose for a car tire? Why?
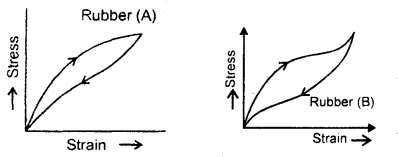
Answer:
Rubber (A) would be used to avoid excessive heating of the car tire.
Question 16.
How are depression and load interrelated in the case of a beam
(a) having rectangular cross-section and loaded in the middle?
Answer:
δ = \(\frac{\mathrm{W} l^{3}}{4 \mathrm{bd}^{3} \mathrm{Y}}\)
(b) having circular cross-section and loaded in the middle?
Answer:
δ = \(\frac{\mathrm{W} l^{3}}{12 \mathrm{Y} \pi \mathrm{r}^{4}}\)
Free Degree and Leading Coefficient Calculator – Find the leading coefficient of a polynomial function step-by-step.
Question 17.
Write copper, steel, glass, and rubber in the order of increasing coefficient of elasticity.
Answer:
Rubber, glass, copper, and steel.
Question 18.
How does Young’s modulus change with rising in temperature?
Answer:
Young’s modulus of a material decreases with rising in temperature.
Question 19.
The length of a wire is cut in half. What will be the effect on the increase in its length under a given load?
Answer:
An increase in length will be reduced to half as Δl ∝ l.
Question 20.
A wire is replaced by another wire of the same length and material but of twice diameter. What will be the effect on the:
(a) increase in its length under a given load?
Answer:
Increase in length will be reduced to one fourth as Δl ∝ \(\frac{1}{\mathrm{r}^{2}}\).
(b) maximum load which it can bear?
Answer:
The maximum bearable load becomes four times as breaking force ∝ area. (= πr²)
Question 21.
Sand does not possess any definite shape and volume, still, it is solid?
Answer:
Sand is a divided rock. It has all properties of solids and even its particles have indefinite volume like amorphous solids.
Question 22.
Name one material that is famous for a large elastic after effect.
Answer:
Glass.
Question 23.
Why some solids have high thermal and electrical conductivity?
Answer:
Because such solids have a large number of free electrons available in them (e.g. metals).
Question 24.
When a wire is bent back and forth, it becomes hot. Why?
Answer:
When a wire is bent back and forth, the deformations are beyond the elastic limit.
Question 25.
Two identical solid balls, one of ivory and the other of wet- clay are dropped from the same height on the floor. Which one will rise to a greater height after striking the floor and why?
Answer:
The ivory ball will rise to a greater height as compared to a clay ball because ivory is more elastic than wet clay.
Question 26.
Define ductile materials.
Answer:
They are defined as materials whose plastic range is relatively large.
Question 27.
Define brittle materials.
Answer:
They are defined as materials whose plastic range is relatively small.
Question 28.
Define elastic fatigue.
Answer:
It is defined as the loss of strength of the material caused due to repeated alternating strains to which the material is subjected.
Question 29.
Define elastic after effect.
Answer:
It is defined as the delay in regaining the original state by a body after the removal of the deforming force.
Question 30.
Define elasticity.
Answer:
It is the property of matter due to which it regains its original shape and size when the deforming forces have been removed.
Question 31.
Define hydrostatic stress.
Answer:
When a body is subjected to a uniform and equal force from all sides, then the corresponding stress is called hydrostatic stress.
Question 32.
Define plasticity.
Answer:
It is defined as the property of matter due to which it does not regain its original shape and size after the removal of deforming forces.
Question 33.
Define tangential or shearing stress.
Answer:
It is defined as the deforming force acting per unit area tangential to the surface.
Question 34.
Define deforming force.
Answer:
It is defined as the external force which when applied to a body changes its configuration (i.e. shape and size).
Question 35.
Define elastic limit.
Answer:
Maximum stress is called the elastic limit.
Question 36.
Define Young’s modulus.
Answer:
Within elastic limits, it is defined as the ratio of normal stress to longitudinal strain.
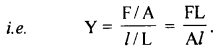
Question 37.
Define compressibility.
Answer:
It is defined as reciprocal of bulk modulus
i. e. compressibility = \(\frac{1}{\mathrm{~K}}=\frac{\Delta \mathrm{V}}{\mathrm{PV}}\)
Question 38.
Define modulus of rigidity.
Answer:
Within elastic limits, it is the ratio of tangential stress (T) to shear strain (θ)
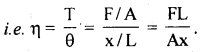
Question 39.
What is the limitation of Hook’s law?
Answer:
It holds good when the wire is loaded within its elastic limit.
Question 40.
What are the factors on which the modulus of elasticity of material depends?
Answer:
Nature of the material and the manner of deforming the wire.
Question 41.
Name the property of a body that opposes its deformation?
Answer:
Elasticity.
Question 42.
Which of the three types of elasticity (Y, K, and t) is possessed by all the three states of the matter?
Answer:
The volume elasticity (K) is possessed by all three states of the matter.
Question 43.
Explain why liquids don’t possess rigidity?
Answer:
Liquids don’t possess rigidity because they have no shape of their own.
Question 44.
A wire of length L and cross-sectional area A is made of a material of Young’s modulus Y. If the wire is stretched by an amount x, then what is the work done?
Answer:
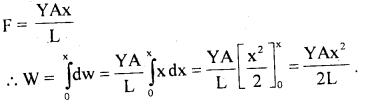
Question 45.
What is the importance of the stress-strain curve?
Answer:
Its slope gives the modulus of elasticity.
Question 46.
A bar is subjected to equal and opposite forces PQ is a plane ‘ making angle θ with the cross-section ‘a’ of the bar. Calculate the tensile stress on PQ.
Answer:
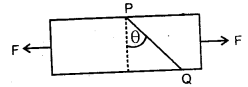
Area PQ = \(\frac{a}{\cos \theta}\)
Tensile stress = \(\frac{\mathrm{F} \cos \theta}{\mathrm{a} / \cos \theta}=\frac{\mathrm{F} \cos ^{2} \theta}{\mathrm{a}}\)
Question 47.
Calculate shearing stress on PQ in Fig.

Answer:
Shearing stress = \(\frac{F \sin \theta}{a / \cos \theta}=\frac{F}{a} \sin \theta \cos \theta=\frac{F}{2 a}(2 \sin \theta \cos \theta)\)
= \(\frac{F}{2a}\) sin 2θ
Question 48.
In a bar is subjected to equal and opposite forces PQ is a plane making angle θ with the cross-section ‘a’ of the bar. Calculate the tensile stress on PQ.when the tensile stress can be maximum?
Answer:
We know that, Tensile stress = \(\frac{\mathrm{F} \cos ^{2} \theta}{\mathrm{a}}\)
For tensile stress to be maximum, cos20 must be maximum – i.e. cos θ = 1 or θ = 0.
Question 49.
In Calculate shearing stress on PQ, when the shearing stress can be maximum?

Answer:Shearing stress = \(\frac{F}{2a}\) sin2θ
For shearing stress to be maximum, sin20 must be maximum
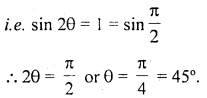
Question 50.
The length of a rod is doubled, under the action of a constant force. If the initial stress is S, then what will be the final stress?
Answer:
We know that stress = \(\frac{F}{A}\) . Also AL = constant for a given rod. When L is doubled, A becomes half, so stress becomes double.
Mechanical Properties of Solids Important Extra Questions Short Answer Type
Question 1.
What are the factors due to which three states of matter differ from one’s Other?
Answer:
Three states of-matter differ from each other due to the following two factors:
(a) The different magnitudes of tester atomic and intermolecular forces.
(b) The degree of random thermal motion of the atoms and molecules of a substance depends upon the temperature.
Question 2.
When we stretch a wire, we have to perform work Why? What happens to the energy given to the wire in this process?
Answer:
In a normal situation, the atoms of a solid are at the locations of minimum potential energy. When we stretch a wire, the work has to be done against interatomic forces. This work is stored in the wire in the form of elastic potential energy.
Question 3.
Why are the bridges declared unsafe after long use?
Answer:
A bridge during its use undergoes alternative strains a large number of times each day, depending upon the movement of vehicles on it. When a bridge is used for a long time it loses its elastic strength, due to which the number of strains in the bridge for given stress will become large and ultimately the bridge may collapse. Thus, !» to avoid this, the bridges are declared unsafe after long use.
Question 4.
Why are the springs made of steel and not of copper?
Answer:
Spring will be a better one if a large restoring force is set up in it on being deformed, which in turn depends upon the elasticity of the material of the spring. Since Young’s modulus of elasticity of steel is more than that of copper, hence steel is preferred in making the springs.
Question 5.
A heavy machine is to be installed in a factory. To absorb vibrations of the machine, a block of rubber is placed between the machinery and the floor. Which of the two rubbers (A) and (B) of Figure would you prefer to use for this purpose? Why?

Answer:
The area of this hysteresis loop measures the amount of heat energy dissipated by the material. Since the area of the loop B is more than that of A, therefore B can absorb more vibrations than that of Av Hence B is preferred.
Question 6.
Metal wires after being heavily loaded dop’\ regain their lengths completely explain why?
Answer:
A material regains its original Configuration (length, shape dr volume) only when the deforming force is within the elastic limit. Beyond the elastic limit, the bodies lose the property of elasticity and hence don’t completely regain the length of being heavily loaded.
Question 7.
Explain. Why spring balances show wrong readings after they have been, Used for a long time?
Answer:
When spring balances are used for a long time, they get fatigued. So the springs of such balances will take time to recover their original configuration. Hence the readings shown by such spring balances will be wrong.
Question 8.
Elasticity is said to be the internal property of matter. Explain.
Answer:
When a deforming force acts on a body, the atoms of the substances get displaced from their original positions. Due to this the configuration of the matter (substance) changes. The moment, the deforming force is removed, the atoms return to their original positions and hence the substance or matter regains its original configuration. Hence elasticity is said to be the internal property of matter.
Question 9.
Define tensor physical quantities. Give an example.
Answer:
They are defined as the physical quantities having different values in different directions e.g. stress.
Question 10.
Define compressional stress.
Answer:
It is defined as the restoring force developed per unit area of cross-section of a body when it is compressed i.e. when its length decreases under the action of deforming force.
Question 11.
Define longitudinal or tensile stress.
Answer:
It is defined as the restoring force developed per unit area of cross-section of a body when the length of the body increases in the direction of the deforming force.
Question 12.

and tell in which significant ways do these curves differ from the stress-strain curve.
Answer:
- Hook’s law is not obeyed at all.
- The elastic region is large here.
- The material does not retrace the same curve while unloading.
Question 13.
Define restoring force.
Answer:
It is defined as the internal force which comes into play from within the body due to which it regains or tends to regain its original configuration.
For a perfectly elastic body restoring force = Deforming force.
Question 14.
Define longitudinal strain.
Answer:
It is defined as the ratio of change in length to the original length of an object when deformed by an external force
i.e. Longitudinal strain = \(\frac{l}{\mathrm{~L}}=\frac{\text { change in length }}{\text { original length }}\)
Question 15.
Define volumetric strain.
Answer:
It is defined as the ratio of change in volume per unit original volume of the body when deformed by an external force change in volume AV
i.e. Volumetric strain = \(\frac{\text { change in volume }}{\text { original volume }}=\frac{\Delta \mathrm{V}}{\mathrm{V}}\)
Question 16.
Define shear strain.
Answer:
It is defined as the ratio of the lateral displacement of a layer to its perpendicular distance from a fixed layer.

Aliter: It is defined as the angle through which a line originally perpendicular to the fixed face gets turned on applying tangential deforming force.
Question 17.
State Hook’s law.
Answer:
Hook’s law: States that within elastic limits, stress is directly proportional to the strain.
i. e. stress ∝ strain
or
\(\frac{\text { Stress }}{\text { Strain }}\) = constant = E.
where E is called coefficient or modulus of elasticity of the material.
Question 18.
Define bulk modulus.
Answer:
Within elastic limits, it is defined as the ratio of normal stress to volumetric strain.
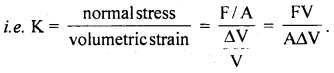
Question 19.
On what factors does the value of the coefficient of elasticity depend? Why it is of it three types?
Answer:
Its value depends upon the:
- nature of the material of the body.
- the way in which the body is deformed.
It is of three types as strain is of three types.
Question 20.
Why a hard wire is broken by bending it repeatedly in opposite direction?
Answer:
It is because of the loss of strength of the material due to repeated alternating strains to which the wire is subjected.
Question 21.
When a cable is cut to half its original length, the maximum load it can withstand does not change. Why?
Answer:
The breaking stress is constant for a given material. Now breaking lord = breaking stress × area. When we cut the cable to half its length, its area of cross-section does not change. Hence there is no effect on the maximum load, the cable can support.
Question 22.
What causes restoring stress when a wire is stretched and when a body is compressed?
Answer:
When a wife is stretched, the restoring stress is caused by inter atomic-attraction and when a body is compressed, the restoring stress is caused by interatomic repulsion.
Question 23.
Are elastic restoring forces conservative?
Answer:
The elastic restoring forces are conservative when the loading and unloading curves coincide, but when these curves are different, the elastic restoring forces are non-conservative.
Question 24.
When a cable is cut to half its original length, how does this affect the elongation under the given load?
Answer:
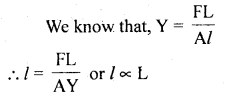
Now as L is made \(\frac{L}{2}\) l will become \(\frac{L}{2}\), so elongation will become half of its value before cutting.
Question 25.
Why do solids have well-defined and reproducible external shapes?
Answer:
It is because, the atoms and molecules are arranged in a definite and regular way throughout the body of the solids, so they have well-defined and reproducible external shapes.
Question 26.
Why any metallic part of the machinery is never subjected to stress beyond the elastic limit of the material?
Answer:
If it is subjected beyond the elastic limit, then a permanent deformation will be set in that metallic part of the machine.
Question 27.
The braking force for a wire is F. What will be the breaking force for
(a) two parallel wires of the same size?
Answer:
When two wires of the same size are suspended in parallel, force F equal to the braking force for a wire will acton each wire if a force 2F is applied on the parallel combination.
(b) for a single wire of double the thickness?
Answer:
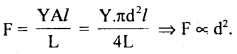
If the thickness is doubled, then the braking force will be four times the braking force.
Question 28.
Elasticity has a different meaning in Physics and in our daily life. Why?
Answer:
In daily life, a body is said to be more elastic if large deformation or strain is produced on subjecting the material to a given stress. But in Physics, it is exactly the opposite. A body is said to be more elastic if a small strain is produced on applying the given stress.
Question 29.
The length of a Wire is increased by 16 cm when a weight of 5 kg is hung. If all conditions are the same, what will be the increase in its length when the diameter is doubled?
Answer:
We know that,
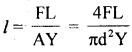
when d = diameter of wire
∴ l ∝ \(\frac{1}{\mathrm{~d}^{2}}\)
Thus when d is doubled, l reduces to \(\frac{1}{4}\)th
i.e. l’= \(\frac{l}{4}=\frac{8}{4}\) = 2 cm. 4 4
Question 30.
When stress is equal to Young’s modulus of elasticity, then calculate the extension of a wire of length l.
Answer:
Here, L = original length of wire.
Let Δl = extension of wire = ?
Stress = Y (given)
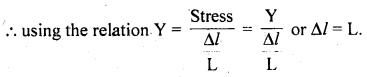
Mechanical Properties of Solids Important Extra Questions Long Answer Type
Question 1.
(a) What are the factors affecting elasticity?
Answer:
The following factors affect the elasticity of a material:
- Effect of hammering and rolling: It causes a decrease in the plasticity of the material due to break¬up of crystal grains into smaller units and hence – the elasticity of the material increases.
- Effect of Annealing: Annealing results in the increases in the plasticity of the material due to, the formation of large crystal grains. Hence the elasticity of the material decreases.
- Effect of the presence of impurities: The effect of the presence of impurities in a material can be both ways i.e. it can increase as well as decrease the elasticity r of the material. The type of effect depends upon the
nature of the impurity present in the material. - Effect of temperature: The increase in the temperature of the material in most cases causes a decrease in the elasticity of the material. The elasticity of invar does not change with the change of temperature.
(b) Define Poisson’s ratio.
Answer:
Poisson’s Ratio (σ): Within elastic limits, it is defined; as the ratio of lateral strain (β) to the linear strain i.e.
σ = \(\frac{β}{α}\)
(c) Define breaking load.
Answer:
Breaking Load: It is defined as the product of the breaking stress and area of cross-section of the given object. It is also called maximum load a body (cable/ wire) can support
i.e. breaking load = Breaking stress × area of cross-section. It should be noted that breaking stress is a constant for the given material.
Question 2.
The length of a metallic wire is L1 when tension is T1 and L2 when tension is T2. Find the original length of the wire.
Answer:
Let L, A be the length and area of the cross-section of the wire.
Also, let l be the extension produced on applying a force F, then
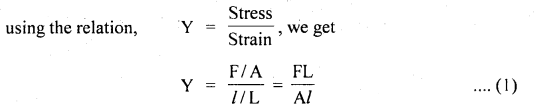
where Y = Young’s modulus.
Now when F = T1 and l = L1 – L.
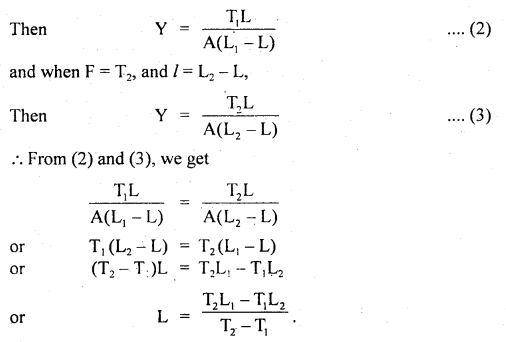
Numerical Problems:
Question 1.
A mass of 5 kg is hung from a copper wire of 1 mm diameter and 2 m in length. Calculate the extension produced. What should be the minimum diameter of the wire so that its elastic limit is not exceeded? Elastic limit for copper = 1.5 × 109 dyne cm-2, Y for copper = 1.1 × 1012 dyne cm-2.
Answer:
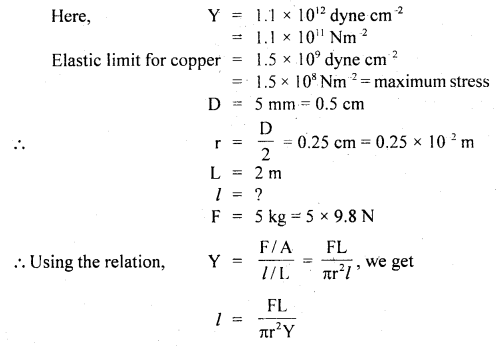
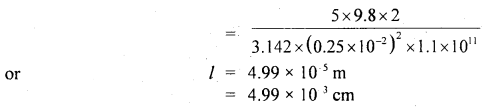
Let d1 be the minimum diameter, then maximum stress
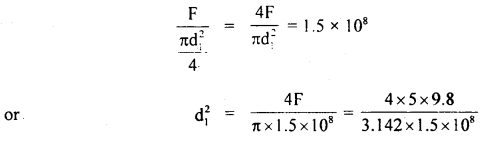
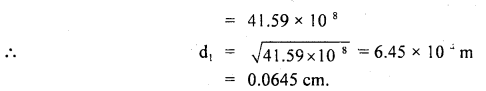
Question 2.
A cube of aluminum of each side 4 cm is subjected to a tangential (shearing) force. The top of the cube is sheared through 0.012 cm w.r.t. the bottom face.
Find (a) shearing strain,
(b) shearing stress,
(c) shearing force. Given η = 2.08 × 1011 dyne cm-2.
Answer:
Here,
length of each side, L = 4 cm
Lateral displacement, x = 0.012 cm ,
η = 2.08 × 1011 dyne cm-2.

Question 3.
The breaking stress of aluminum is 7.5 × 108 dyne cm-2. Find the greatest length of aluminum wire that can be hung vertically without breaking. The density of aluminum is 2.7 g cm-3. Take g = 980 cm s-2.
Answer:
Here, breaking stress = 7.5 × 108 dyne cm-2, ρ = 2.7 g cm-3
Let l be the greatest length of the wire that can be hung vertically without breaking.
mass of wire, m = area of cross-section × length × density = a /ρ.
∴ Weight of wire, W = mg = a / ρ g.
This is equal to the maximum force that the wire can withstand.
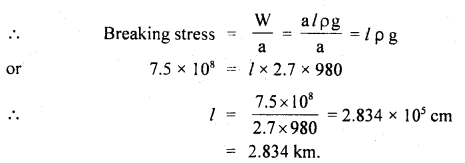
Question 4.
Calculate the % increase in the length of a wire of diameter 2,5 unstretched by a force of 100 kg. Y for the wire = 12,5 × 1011 dyne cm-2.
Answer:
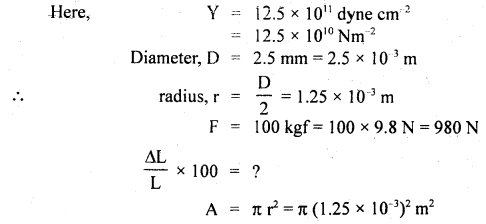
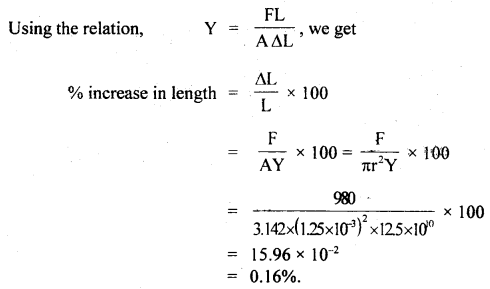
Question 5.
Compare the densities of water at the surface and bottom of a lake 1oo m deep, given that the compressibility is \(\frac{10^{3}}{22}\) per atm and 1 atm = 1.015 × 105 Pa.
Answer:
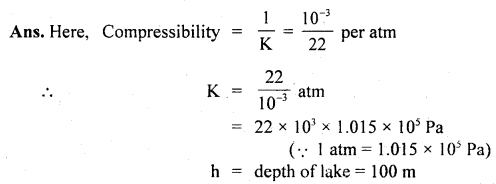
Let V = Volume of 1 kg water at the surface.
V’ = Volume of 1 kg water at the bottom of lake 100 m deep
= V – ΔV, where ΔV = decrease in volume, increase in pressure, P = hρg = 100 × 103 × 9.8 Nm2
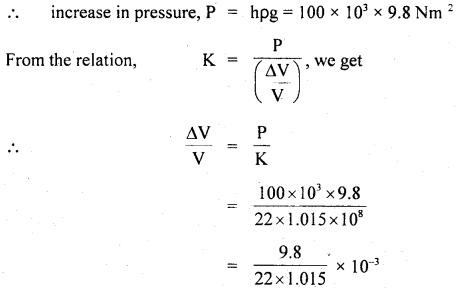
If ρs and ρb be the densities of water at the surface and at the bottom of the lake respectively, then
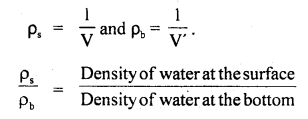
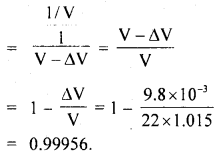
Question 6.
A steel wire 2 mm in diameter is stretched between two clamps, when its temperature is 40° C. Calculate the tension in the wire, when its temperature falls to 30° C. Given, coefficient of linear
Answer:

If Δl be the change n length of the wire, then
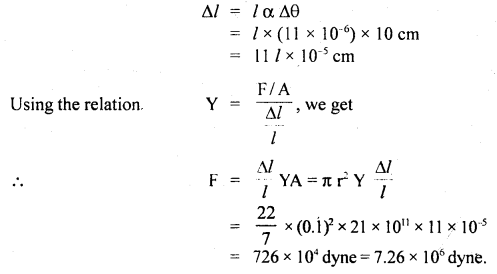
Question 7.
When a weight W is hung from one end of a wire of length L (other end being fixed), the length of the wire increases by l fig. (a). If the wire is passed over a pulley and two weights W each is hung at the two ends fig. (b), what will be the total elongation in the wire?
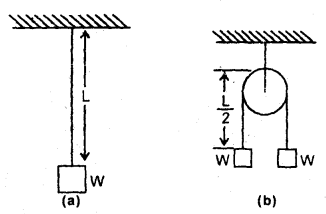
Answer:
(a) Let Y = Young’s modulus of the material of the wire. If ‘a’ be its area of cross-section, then
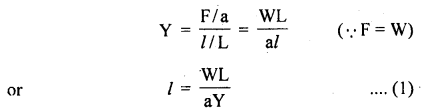
(b) When the wire is passed over the pulley, let l’ be the increase in the length of each segment. Since \(\frac{L}{2}\) = length of each segment.
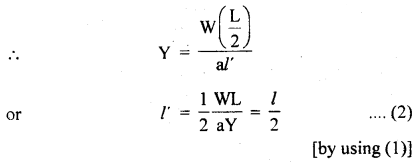
∴ Total increase in the length of the wire is given by
= l’ + l’ = 2l’ = 2 × \(\frac{l}{2}\) = l.
Question 8.
A uniform cylindrical wire is subjected to longitudinal tensile stress of 5 × 107 Nm-2. The Young’s Modulus of the material of the wire is 2 × 1011 Nm-2. The volume change in the wire is 0.02%. Calculate the fractional change in the radius of the wire.
Answer:
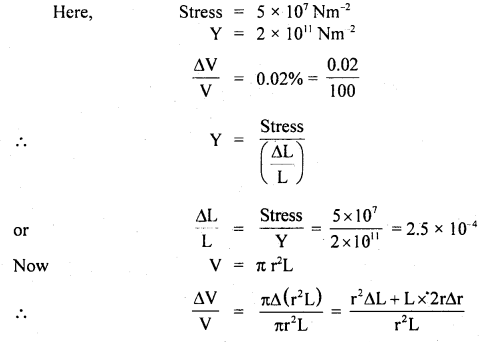
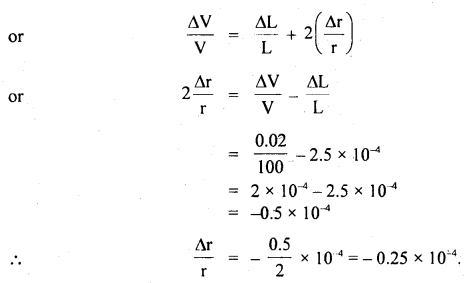
Question 9.
A wire loaded by the weight of density 7.6 g cm-3 is found to measure 90 cm. On immersing the weight in water, the length decreases by 0.18 cm. Find the original length of the wire.
Answer:
Let L = original length of the wire =?
A = be its area of cross-section.
W = load attached to the wire.
Then Young’s Modulus of the wire is given by
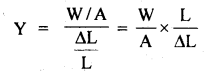
Here, ΔL = 90 – L = Change in the length of wire.
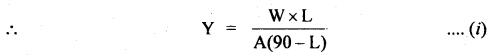
Volume of weight attached,
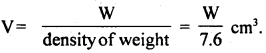
∴ Mass of water displaced = V × density of water
= \(\frac{W}{7.6}\) × l = \(\frac{W}{7.6}\)
∴ Net weight after immersing in water ¡s
W’ = W – \(\frac{W}{7.6}\) = \(\frac{6.6}{7.6}\) W
Length of wire after immersing ¡n water
= 90 – 0.18 = 89.82 cm.
∴ Increase in length on immersing in water,
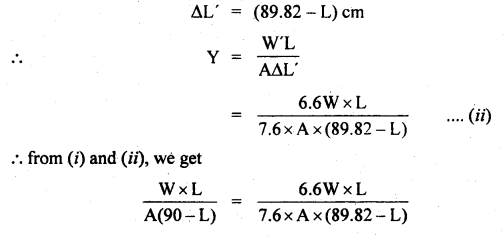

Question 10.
Two exactly similar wires of steel and copper are stretched by equal forces. If the total elongation is 1 cm, find by how much each wire is elongated. Given Y for steel = 20 × 1011 dyne cm-2, Y for copper = 12 × 1011 dyne cm-2.
Answer:
Let Δls and Δlc be the elongation produced in steel and copper wires respectively.
Ls, Lc be their respective lengths,
Ls = Lc (∵ wires are similar)
Ys = 20 × 1011 dyne cm-2
Yc = 12 × 1011 dyne cm-2
Δls + Δlc = 1 cm
A = area of cross-section of each wire.
F = equal force applied.
∴ Using the relation,
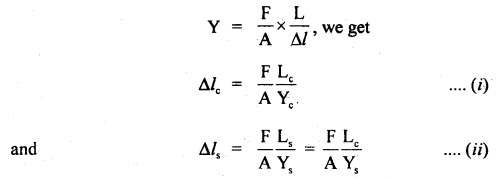
Dividing (ii) by (i), we get
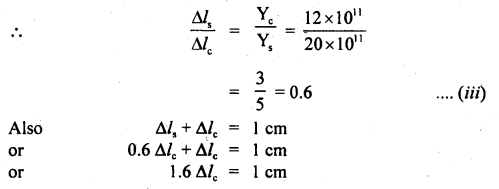
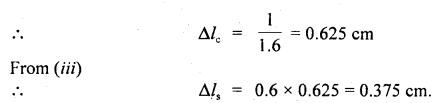
Question 11.
A rubber rope of length 8 m is hung from the ceiling of a room. What is the increase in the length of the rope due to its own weight? Given Young’s modulus of elasticity of rubber is 5 × 106 Nm-2 and density of rubber = 1.5 × 103 kg m-3. Take g = 10 ms-2.
Answer:
Here, ρ = 1.5 × 103 kg m-3
L = 8m
Y = 5 × 106 Nm-2
Let Mg and A be the weight and area of the cross-section of the rubber rope.
As weight acts at C. G. so effective length = \(\frac{L}{2}\)
∴ Mg = A L ρ g (∵ M is distributed over L)
Let ΔL = increase in the length of the rope =?
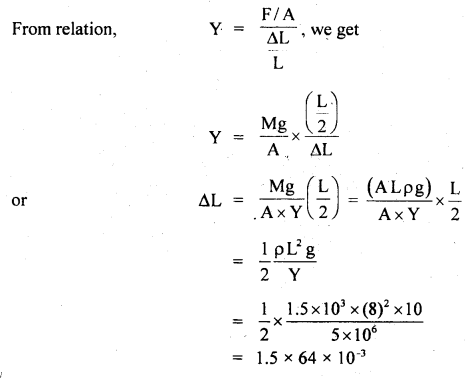
![]()
Question 12.
A sample of bone in the form of a cylinder of cross-sectional area 1.5 cm2 is loaded on its upper end by a mass of 10 kg. By careful measurements with a traveling microscope, the length of the cylindrical sample is observed to decrease by 0.0065%. Calculate the value of Young’s Modulus for the specimen. Given g = 9.8 ms-2.
Answer:

Question 13.
Estimate the maximum height of a mountain.
Answer:
The elastic behavior of the earth helps us to calculate the maximum height of mountains on earth.
Let h be the height of a mountain.
ρ = density of rocks of the mountain
∴ The pressure at the base of the mountain h ρ g = Stress
The elastic limit of a typical rock 3 × 108 Nm-2
The stress must be less than the elastic limits, otherwise, the rock-begins to sink.

It may be noted that the height of Mount Everest is nearly 9 km.
Question 14.
A uniform pressure P is exerted on all sides of a solid cube. It is heated through t°C in order to bring its volume back to the value it had before the application of pressure. Find the value of t.
Answer:
Let γ = coefficient of cubical expansion of the cube.
Let K be the bulk modulus of elasticity of its material.
V = initial volume.
P = pressure applied.
ΔV = Decrease in its volume.
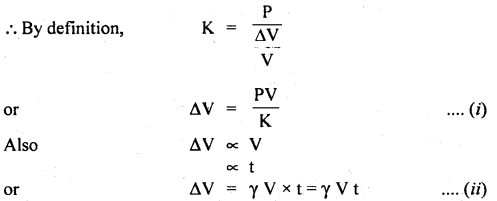
where t = rise in its temperature so as to increase the volume by ΔV s.t. it is brought back to its initial volume.
∴ From (i) and (ii), we get
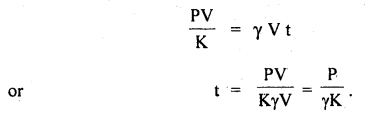
Question 15.
If K be the bulk modulus of a metal and a pressure P is applied uniformly on all its sides. If p be the density of metal, then find the fractional increase in its density.
Answer:
Let M = mass of metal
V = mass of volume
∴ ρ = \(\frac{M}{V}\) ….(i)
Let ΔV = Decrease in its volume when a pressure P is applied.
If ρ’ be its new density, then
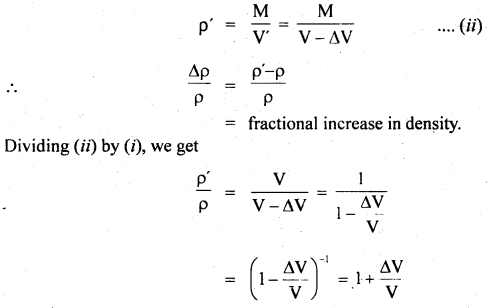

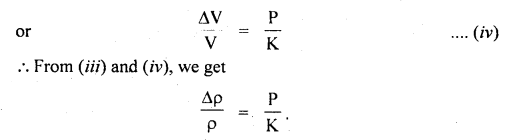
Question 16.
The rubber cord catapult has a cross-sectional area of 1 mm2 and a total unstretched length of 10 cm. It is stretched to 12 cm and then released through a projectile of the mass of 2 gm. Taking Y =5 × 108 Nm-2, find tension ¡n the cord and velocity of projection.
Answer:
Here, Y = 5 × 108 Nm-2
A = 1mm2 = 10-6 m2
L = 10 cm = 0.1 m
Δl = 12 – 10 = 2cm = 0.02m
m = 2 × 10-3 kg
T =?
V =?

This is converted into K.E. of the projectile.
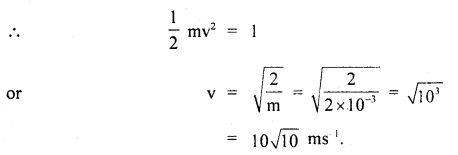
Question 17.
What should be the greatest length of a steel wire which when fixed at one end can hang freely without breaking? Density (ρ) of steel = 7.8 g cm3, breaking stress for steel = 7.8 × 109 dynes/cm2.
Answer:
Here, breaking stress = 7.8 × 109 dyne cm2
Le.t A = area of cross-section of the wire
ρ = 7.8 g cm-3
g = 980 cms-2
Let l = length required = ?
∴ V = volume of wire = lA
∴ Stretching force = weight of the wire = ρ V g
= ρlAg
∴Maximum stress = Breaking stress

Question 18.
A copper wire of negligible mass, area of cross-section 10-6 m2, and length 1 m are kept on a smooth horizontal table with one end fixed. A ball of mass 1 kg is attached to the other end. The wire and ball are rotating with an angular velocity of 20 rad s-1. If the elongation in the wire is 10-3 m, then find Young’s modulus.
Answer:
Here, L = original length of the wire = 1 m
l = elongation length of the wire = 10-3 m
A = area of cross-section of wire = 10-6 m2
M = mass of ball attached to the wire = 1 kg
ω = angular velocity of rotation = 20 rad s-1
Y = ?
Force on wire = centripetal force
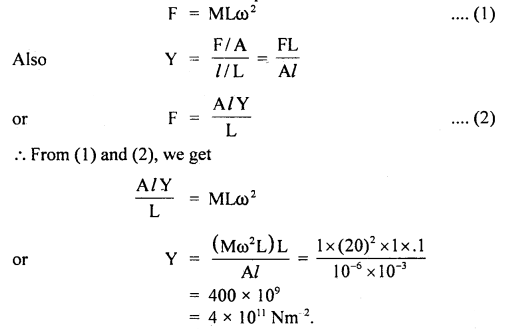
Question 19.
If the angular velocity of the wire and the ball in the above question is increased to Loo rad s, then the wire breaks down. Calculate the breaking stress.
Answer:
As per above question M = 1 kg
L = 1m .
A = 10-6 m2
Here, ω = angular velocity = 100 rad s-1
Breaking stress = ?
Using the formula,
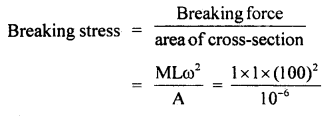
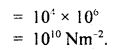
Question 20.
A wire of radius r stretched without tension along a straight line is tightly fixed at points A and B as shown in the figure. What is the tension in the wire when it is pulled into the shape XYZ?
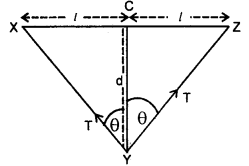
Answer:
Let T = Tension in the wire = ?
r = radius of the wire
∴ A = area of cross-section of the wire = πr²
θ = ∠XYC = ∠ZYC
l = X C = CZ
If Δl be the extension of the wire, then
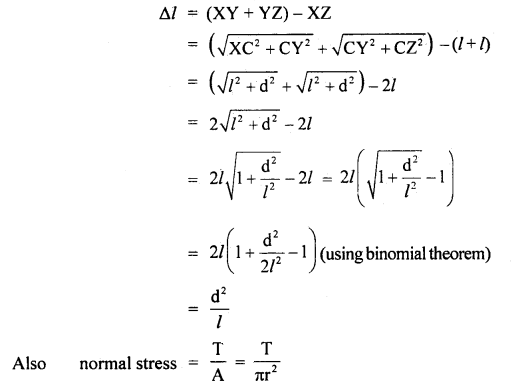
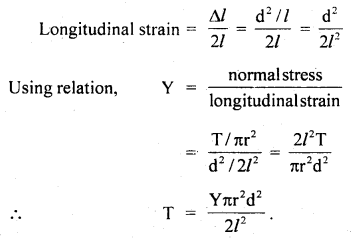
Question 21.
A wire of density 9 g cm-3 is stretched between two clamps 100 cm apart, while subjected to an extension of 0.05 cm. What is the lowest frequency of transverse vibrations in the wire, assuming Y = 9 × 1011 dyne/cm2?
Answer:
Here, ρ = density of wire = 9 g cm3
Y = 9 × 1011 dyne/cm2
L = distance between two clamps = 100 cm
l = extension of wire = 0.05 cm
Let v = lowest frequency of transverse vibrations = ?
If F and A be the stretching force and area of the cross-section of the wire, then
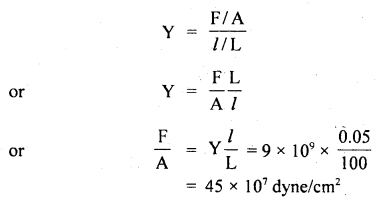
Also, the lowest frequency or fundamental frequency of transverse vibrations is given by
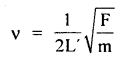
where L’ = 100 + 0.05 = 100.05 cm
m = mass/length = Aρ = area × density
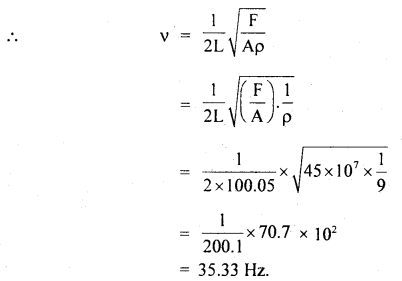
Question 22.
A steel wire with a cross-sectional area of 0.5 mm2 is held between two fixed supports. If the tension in the wire is negligible and it is just taut at a temperature of 20°C. Determine the tension when the temperature falls to 0°C. Y = 21 × 1011 dyne/cm2 and coefficient of linear expansion is 12 × 10-6 per degree centigrade. Assume distance between two supports. remains same.
Answer:
Here, let L = length of the wire
A = its area of cross-section = 0.5mm2
= 0.005 cm2
Y = 21 × 1011 dyne/cm2
α = coefficient of linear expansion
= 12 × 10-6 °C-1
Let T = tension in the wire = ?
If Δl be extension, then
Δl = α L Δt
where Δt = 20 – 0 = 20°C
![]()
This strain is tensile as the wire is kept taut and not allowed to contract.
∴ Tensile stress in the wire = Y × strain
= Y α Δt
∴ T = Tensile stress × A
= Y α Δt A
= 21 × 1011 × 12 × 10-6 × 20 × 0.005
= 25.2 × 105 dyne.
Question 23.
Two rods of different metals having the same area of cross-section A are placed between the two fixed points and they have the parameters as l1, α1, Y1, and l2, α2, Y2 respectively where l stands for their lengths, a for coefficients of linear expansion. The temperature of both is increased by T°C. Find the force with which the rods act on each other.

Answer:
Due to the rise in temperature by T°C, let Δl1 and Δl2, be the increase in lengths of the two rods.
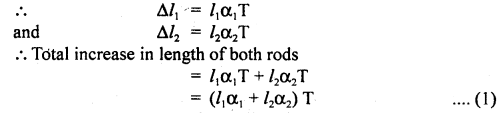
As the two fixed points don’t allow the length to increase, hence thermal stress \(\frac{F}{A}\) is developed.
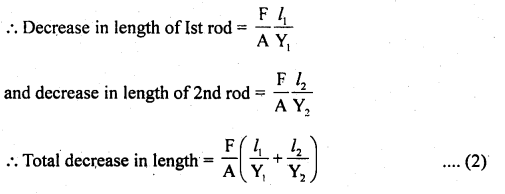
∴ Decrease in length due to thermal stress = increase in length due to thermal linear expansion
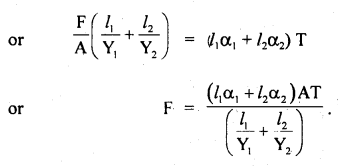
Question 24.
Two rods of different materials having coefficients of linear expansion α1 and α2 and Young’s modulus Y1 and Y2 respectively are fixed between two massive points and are heated such that they undergo the same increase in temperature. There is no bending in rods of α1: α2 = 2: 3 and thermal stresses produced in two rods are equal. Calculate the ratio Y1: Y2.
Answer:
It is a common cause of thermal expansion and elastic compression.
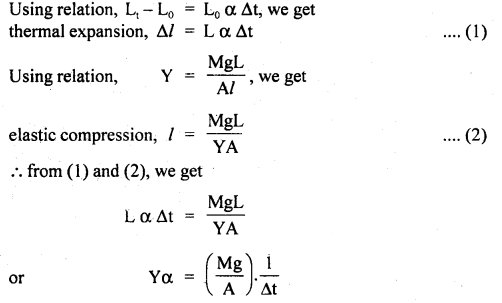
For the same rise in temperature (Δt) and same stress,
Yα = constant
or
Y1α1 = Y2α2
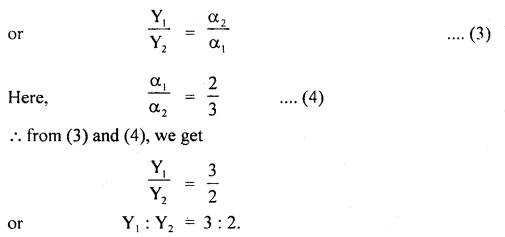
Question 25.
What force is required to stretch a copper wire 1 cm2 in cross¬section to double its length? Y for copper is 1.26 × 1012 dyne cm-2.
Answer:
Here, A = 1 cm2
Let L = length of the wire.
Also, Let L’ be the new length when a stretching force F is applied.
L’ = 2L
Then l = extension = L’ – L = 2L – L = L
F = ?
Y = 1.26 × 1012 dyne cm-2
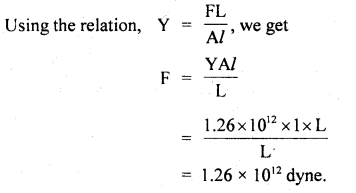
Value-Based Type:
Question 1.
Raman and his friend Sbhan while going to the school on a motorcycle noticed that a bridge had collapsed. Immediately they went to their physics teacher and enquired about the reasons for falling off the bridge. After knowing the reasons that very interesting; they decided to pursue their career as civil engineers and vowed to construct 100% quality dams and bridges.
(a)Comment upon the values possessed by them.
Answer:
Sympathy, determination, and concern for society, honesty, and integrity.
(b) Name the property that helps in constructing bridges. Also, define the property.
Answer:
Elasticity: The property of the body to regain its original configuration (i .e length, volume, or shape) when the deforming force is removed, is called elasticity.
Question 2.
Ram and his friend Ramesh are the students of class XI. They are discussing “elastic fatigue”. Ram told that just as a tired person elastic body also relieved of the fatigue or regains its original degree of elasticity when allowed to rest for some time. Raman did not convince Ram. They went to solve this problem before their physics teacher.
(i) What values are displayed by Ram and Ramesh?
Answer:
The values displayed by them are:
(a) Curiosity
(b) Awareness
(c) Attitude to find the solution by discussion
(d) Interested in learning.
(ii) Whether Ram’s ideas and reasons were correct or not?
Answer:
Yes, Ram’s ideas and reasons were correct and were recommended by their teachers.
(iii) Why do spring balance shows wrong readings after they have been used for a long time?
Answer:
This is due to elastic fatigue.
Question 3.
Kamal read a topic in a newspaper that a bridge declared unsafe by the Government. The bridge was 2 km away from his house and he used to cross it almost daily. The condition of the bridge does not look so bad. However, it was built 60 years ago. The next day Kamal asked the reason for this question to his friends.
(i) What value is displayed by Kanal here?
Answer:
Values displayed are:
Curiosity, awareness, group discussion, and keenness to know the scientific reasons.
(ii) Why the bridge declared unsafe after long use?
Answer:
Due to the repeated stress and strain, the material used in the bridges loses elastic strength and ultimately may collapse. Hence, bridges are declared unsafe after long use.
Question 4.
Two friends Mohan and Dinesh arc discussing elasticity. Mohan told that steel is more elastic than rubber. Dinesh was surprised and asked his teacher the-Fcascm-Jachind it.
(i) What value is displayed by Dinesh?
Answer:
The values displayed by Dinesh are:
Curiosity, Interested in learning.
(ii) How his teacher explained it?
Answer:
Let the two pieces of wire, one of steal and the other of rubber having an equal length (L) and equal area of cross-section (A). Let each be stretched by equal force (F).
Then, Young’s modulus of steel and rubber are:
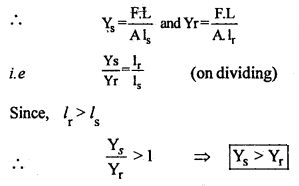
Hence, Steal is more elastic than rubber.