Here we are providing Class 11 Physics Important Extra Questions and Answers Chapter 11 Mechanical Properties of Fluids. Important Questions for Class 11 Physics with Answers are the best resource for students which helps in Class 11 board exams.
Class 11 Physics Chapter 11 Important Extra Questions Thermal Properties of Matter
Thermal Properties of Matter Important Extra Questions Very Short Answer Type
Question 1.
The fact that the triple point of a substance is unique is used in modern thermometry. How?
Answer:
In modern thermometry, the triple point of water is a standard fixed point.
Question 2.
Is it possible for a body to have a negative temperature on the Kelvin scale? Why?
Answer:
No. Because absolute zero of temperature is the minimum possible temperature on the Kelvin scale.
Question 3.
(a) Why telephone wires are often given snag?
Answer:
It is done to allow for safe contraction in winter.
(b) The temperature of a gas is increased by 8°C. What is the corresponding change on the Kelvin scale?
Answer:
8 K.
Question 4.
There ¡s a hole in a metal disc. What happens to the size of the hole if the metal disc is heated?
Answer:
The size of the hole increases on heating the metal disc.
Question 5.
Milk is poured into a cup of tea and is mixed with a spoon. Is this an example of a reversible process? Why?
Answer:
No. When milk is poured into tea, some work is done which is not recoverable. So the process is not reversible.
Question 6.
The top of a lake is frozen. Air ¡n contact with it is at -15°C. What do you expect the maximum temperature of water in contact with the lower surface ice? What do you expect the maximum temperature of water at the bottom of the lake?
Answer:
0°C, 4°C.
Question 7.
How does the heat energy from the sun reaches Earth?
Answer:
It reaches by radiation.
Question 8.
Why does not the Earth become as hot as the Sun although it has been receiving heat from the Sun for ages?
Answer:
Earth loses heat by convection and radiation.
Question 9.
Why felt rather than air is employed for thermal insulation?
Answer:
In the air, loss of heat by convection is possible. But convection currents cannot be set up in felt.
Question 10.
What are the three modes of transmission of heat energy from one point to another point?
Answer:
Conduction, Convection and Radiation.
Question 11.
Name suitable thermometers for measuring:
(a) – 80°C,
Answer:
gas thermometer,
(b) 50°C,
Answer:
mercury thermometer,
(c) 700°C,
Answer:
Platinum resistance thermometer,
(d) 1500°C.
Answer:
radiation pyrometer.
Question 12.
Why a thick glass tumbler cracks when boiling liquid is poured into it?
Answer:
Its inner and outer surfaces undergo uneven expansion due to the poor conductivity of glass, hence it cracks.
Question 13.
What is the basic principle of a thermometer?
Answer:
The variation of some physical property of a substance with temperature constitutes the basic principle of the thermometer.
Question 14.
Out of mass, radius and volume of a metal ball, which one suffers maximum and minimum expansion on heating? Why?
Answer:
Volume and radius suffer maximum and minimum expansions respectively as γ = 3α.
Question 15.
The higher and lower fixed points on a thermometer are separated by 160 mm. If the length of the mercury thread above the lower point is 40 mm, then what is the temperature reading?
Answer:
The temperature reading = \(\frac{100 \times 40}{160}\) =25.
Question 16.
Two thermometers are constructed in the same way except that one has a spherical bulb and the other an elongated cylindrical bulb. Which of the two will respond quickly to temperature changes.
Answer:
The thermometer with a cylindrical bulb will respond quickly as the area of the cylindrical bulb is greater than the area of the spherical bulb.
Question 17.
Why a gas is cooled when expanded?
Answer:
Due to a decrease in internal energy, gas is cooled.
Question 18.
Why two layers of cloth of equal thickness provide warmer covering than a single layer of cloth of double thickness?
Answer:
This is because the air enclosed between the two layers of cloth acts as a good heat insulator.
Question 19.
Why snow is a better heat insulator than ice?
Answer:
Snow has air enclosed in it which reduces the chances of loss of heat by convection, hence it is a better heat insulator than ice.
Question 20.
Why water in a metallic pot can be boiled quickly if the bottom of the pot is made black and rough than a highly polished surface?
Answer:
The black and rough surface is a better absorber of heat than a highly polished surface.
Question 21.
Pieces of glass and copper are heated to the same temperature. Why does the piece of copper feel hotter OIL touching?
Answer:
Since copper is a better conductor of he, than gases, so copper transmits heat quickly to the hand and hence it feels hotter on touching.
Question 22.
Why people in the desert wear heavy clothes?
Answer:
Because they protect them from both heat and cold.
Question 23.
Why a wooden table fixed with iron nails become loose after some time?
Answer:
Due to uneven expansion of wood and nail.
Question 24.
Wooden charcoal and a metal piece of the same dimension are heated in the same oven to the same temperature and then removed in the dark. Which one would shine more and why?
Answer:
The charcoal will shine more as it is a good absorber and good emitter, so it will emit more energy.
Question 25.
What is the condition for the difference between the length of a certain brass rod and that of a steel rod to be constant at all temperature?
Answer:
The condition is that the lengths of the rods are inversely proportional to the coefficients of linear expansion of the materials of the rods.
Question 26.
What is the cause of the hotness of a body?
Answer:
The K.E. of the molecules constituting the body causes its hotness.
Question 27.
When are two bodies said to be in thermal equilibrium?
Answer:
Two bodies are said to be in thermal equilibrium when they are at j the same temperature.
Question 28.
What is the value of the temperature coefficient for metals and alloys?
Answer:
Its value is always positive fc > r metals and alloys.
Question 29.
What is the value of the temperature coefficient for insulators and semi-conductor?
Answer:
It is always negative for insulators and semiconductors.
Question 30.
Are Coefficients of thermal expansion constant for a given solid?
Answer:
No.
Question 31.
Out of a gas and mercury thermometer, which one is more sensitive?
Answer:
A gas thermometer is more sensitive.
Question 32.
At what temperature will wood and iron appear equally hot or equally cold?
Answer:
At the temperature of the human body, both wood and iron will appear equally hot or cold.
Question 33.
A liquid of cubical coefficient of expansion is heated in a vessel having a coefficient of linear expansion \(\frac{\gamma}{3}\). What would be the effect on the level of liquid?
Answer:
No effect.
Question 34.
Is a fur coat itself a source of heat or merely an insulator?
Answer:
It is merely an insulator.
Question 35.
Why fur coat is an insulator?
Answer:
Because it is a bad conductor of heat and prevents the outflow of body heat.
Question 36.
Why does a bullet heat up when it hits a target?
Answer:
It is because its K.E. is converted into heat energy.
Question 37.
How can you measure a temperature of less than 100 K?
Answer:
It can be measured by using a germanium resistance thermometer.
Question 38.
Why water at the bottom of a waterfall is warmer than at the top?
Answer:
It is because P.E. of stored water is converted into heat energy.
Question 39.
What is the S.I. unit of heat capacity?
Answer:
Joule/Kelvin (JK-1) is the S.I. unit of heat capacity.
Question 40.
Name the substance that contracts on heating?
Answer:
Ice.
Question 41.
Why is a vacuum created between two glass walls of a thermos flask?
Answer:
It is done to prevent the transfer of heat by conduction and convection.
Question 42.
What happens to the K.E. of water which stops after being stirred?
Answer:
It is converted into heat energy.
Question 43.
Why do telephone wires become tight in winter?
Answer:
It becomes tight due to contraction in length with the fall of temperature.
Question 44.
How does the coefficient of cubical expansion of a gas changes with temperature?
Answer:
It decreases with the rise in temperature.
Question 45.
Why do dogs draw out their tongues in summer?
Answer:
They do so to create cooling by evaporation.
Question 46.
How does the boiling point of a liquid changes with temperature?
Answer:
It rises with an increase in temperature.
Question 47.
What is the effect of pressure on the melting point of ice?
Answer:
It is lowered due to the increase in pressure.
Question 48.
What is the thermal capacity of 40 g of copper of specific heat 0.3?
Answer:
It is for 12 cal.
Question 49.
When water is heated from 0° to 10°C, what happens to its volume?
Answer:
It first decreases and then increases.
Question 50.
Why the coefficient of cubical expansion of water is zero at 4°C?
Answer:
This is because the density of water is maximum at 4°C.
Thermal Properties of Matter Important Extra Questions Short Answer Type
Question 1.
Why gas thermometers are more sensitive than mercury thermometers?
Answer:
This is because the coefficient of expansion of a gas is very large as compared to the coefficient of expansion of mercury. For the same temperature change, the gas would undergo a much larger change in volume as compared to mercury.
Question 2.
Why the brake drum of an automobile gets heated up when the automobile moves down a hill at constant speed?
Answer:
Since the speed is constant so there is no change of kinetic energy. The loss in gravitational potential energy is partially the gain in the heat energy of the brake drum.
Question 3.
A solid is heated at a constant rate. The variation of temperature with heat input is shown in the figure here:
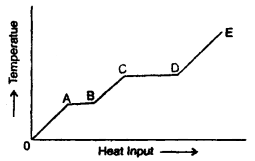
(а) What is represented by AB and CD?
Answer:
The portions AB and CD represent a change of state. This is because the supplied heat is unable to change the temperature. While AB represents a change of state from solid to liquid, the CD represents a change of state from liquid to vapour state.
(b) What conclusion would you draw1 if CD = 2AB?
Answer:
It indicates that the latent heat of vaporisation is twice the latent heat of fusion.
(c) What is represented by the slope of DE?
Answer:
Slope of DE represents the reciprocal of the thermal or heat capacity of the substance in vapour state i.e. slope 0f DE = \(\frac{d T}{d Q}=\frac{1}{m C}\)(∴ dQ = mCΔT).
(d) What conclusion would you draw from the fact that the slope of OA is greater than the slope of BC?
Answer:
Specific heat of the substance in the liquid state is greater than that in the solid-state as the slope of OA is more than that of BC i.e. \(\frac{1}{\mathrm{mC}_{1}}\) > \(\frac{1}{\mathrm{mC}_{2}}\) where C1, C2 are specific heats mC1 mC2 of the material in solid and liquid state respectively.
Question 4.
Define:
(a) Thermal conduction.
Answer:
It h defined as the process of the transfer of heat energy from one part of a solid. to another part at a lower temperature without the actual motion of the molecules. It is also called the conduction of heat.
(b) Coefficient of thermal conductivity of a material.
Answer:
It is defined as the quantity of heat flowing per second across the opposite faces of a unit cube made of that material when the opposite faces are maintained at a temperature difference of 1K or 1°C.
Question 5.
On what factors does the amount of heat flowing from the hot face to the cold face depend? How?
Answer:
If Q is the amount of heat flowing from hot to the cold face, then it is found to be:
- directly proportional to the cross-sectional area (A) of the face
i. e. Q ∝ A …(1) - directly proportional to the temperature difference between the two faces, i.e. Q ∝ Δθ ….(2)
- directly proportional to the time t for which the heat flows i.e. Q ∝ t …. (3)
- inversely proportional to the distance ‘d’ between the two faces
i.e. Q ∝ \(\frac{1}{Δx}\) …(4)
Combining factors (1) to (4), we get
Q ∝ \(\frac{\mathrm{A} \Delta \theta}{\Delta \mathrm{x}}\)t
or
Q ∝ K A \(\frac{\Delta \theta}{\Delta \mathrm{x}}\)t
where K is the proportionality constant known as the coefficient – of thermal conductivity.
Question 6.
State Newton’s law of cooling and define the cooling curve. What is its importance?
Answer:
Newton’s law of cooling: States that the rate of loss of heat per unit surface area of a body is directly proportional to the temperature difference between the body and the surroundings provided the difference is not too large.
Cooling Curve: It is defined as a graph between the temperature of a body and the time. It is as shown in the figure here.
The slope of the tangent to the curve at any point gives the rate of fall of temperature.
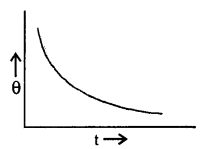
Question 7.
Explain why heat is generated continuously in an electric heater but its temperature becomes constant after some time?
Answer:
When the electric heater is switched on, a stage is quickly reached when the rate at which heat is generated by an electric current becomes equal to the rate at which heat is lost by conduction, convection and radiation and hence a thermal equilibrium is established. Thus temperature becomes constant.
Question 8.
A woollen blanket keeps our body warm. The same blanket if wrapped around ice would keep ice cold. How do you explain this apparent paradox?
Answer:
Wool is a bad conductor of heat. Moreover wool encloses air in it which is a bad conductor. There can also be no loss of heat by convection. The woollen blanket keeps us warm by preventing the heat of the human body to flow outside and hence our body remains warm.
In the case of ice, the heat from outsiders prevented to flow inside and thus ice remains cold.
Question 9.
A liquid is generally heated from below. Why?
Answer:
When a liquid is heated, it becomes rarer due to a decrease in density and it rises up. Liquid from the upper part of the vessel comes down to take its place and thus convection currents are formed. If the liquid is heated at the top, no such convection currents will be formed and only the liquid in the upper part of the vessel will become hot. However, the temperature in the lower part of the vessel will rise slightly due to a small amount of heat conducted by the hot liquid in the upper part of the vessel.
Question 10.
If a drop of waterfalls on a very hot iron, it does not evaporate fora long time. Why?
Answer:
When a drop of waterfalls on a very hot iron, it gets insulated from the hot iron due to the formation of a thin layer of water vapour, which is a bad conductor in nature. It takes quite a long to evaporate as heat is conducted from hot iron to the drop through the layer of water vapour very slowly.
On the other hand, if a drop of waterfalls on an iron which is not very hot, then it comes in direct contact with the iron and evaporates immediately.
Question 11.
On a hot day, a car is left in sunlight with all the windows closed. After some time, it is found that the inside of the car is considerably warmer than the air outside. Explain why?
Answer:
Glass possesses the property of selective absorption of heat radiation. It also transmits about 50% of heat radiation coming from a hot source like the sun and is more or less opaque to the radiation from moderately hot bodies (at about 100°C or so). Due to this, when a car is left in the sun, heat radiation from the sun gets into the car but as the temperature inside the car is moderate, it cannot escape through its windows. Thus glass windows of the car trap the sun rays and because of this, the inside of the car becomes considerably warmer.
Question 12.
It takes longer to boil water with a flame in a satellite in gravitational field-free space, why? How it will be heated?
Answer:
Water boils with flame by the process of convection. Hot lighter particles raise up and heavier particles move down under gravity. In. a gravity-free space in the satellite, the particles cannot move down hence, water can’t be heated by convection.
It will be heated by conduction.
Question 13.
Find γ for polyatomic gas and hence determine its value for a triatomic gas in which the molecules are linearly arranged.
Answer:
The energy of a polyatomic gas having n degrees of freedom is given by
E = n × \(\frac{1}{2}\) kT × N =\(\frac{n}{2}\) RT
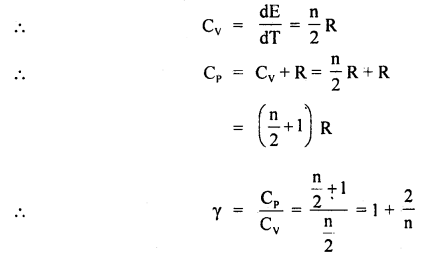
In case of a triatomic gas, n = 7
∴ γ = 1 + \(\frac{2}{7}\) = \(\frac{9}{7}\).
Question 14.
Food in a hot case remains warm for a long time during winter, how?
Answer:
The hot case is a double-walled vessel. The space between the walls is evacuated in a good hot case. The food container placed inside the hot case is made of crowning steel, thus neither the outside low-temperature air can enter the container nor the heat from inside can escape through the hot case by conduction or convection. The highly polished shining surface of the food container helps in stopping loss of heat due to radiation. Thus, the heat of the food is preserved for a long time and food remains hot in winter.
Question 15.
You might have seen beggars sleeping on footpaths or in open in winter with their hands and knees pulled inside. Similarly dogs too curl while sleeping in winter. How does such action help anybody?
Answer:
The heat radiated or emitted from a body at a given temperature depends on
- the temperature difference between the body and the surrounding,
- area of the body in contact with the surroundings and
- the nature of the body.
For man and animals in winter (1) and (2) factors remain what they are. So, in order to preserve, their body heat they curl up to reduce the surface area in contact with cold air.
Question 16.
Many people enjoy bathing below Kempty fall in Mussoorie, even though the water is quite cold, explain?
Answer:
When water falls from a height, it loses its potential energy. This is converted into the kinetic energy of the water molecules. It is a known fact from the kinetic theory of gases that an increase in kinetic energy of the substance increases its temperature, hence the temperature of water at the bottom of the fall rises and it does not remain as cold as on the top. Therefore, people taking bath below the Kempty fall do not get frozen, they rather feel warm and enjoy bathing.
Question 17.
Cycle, scooter handles and steering wheels of four-wheelers have plastic, rubber or cotton thread coverings. Why?
Answer:
Cycle and scooter handle, as well as steering wheels of four-wheelers such as car, truck, tempo, are made of metals which are good conductors of heat. In winter when we hold them the body heat is conducted to them being at lower temperature and in summer their temperature is more than the body temperature, transfer heat to the human hands. In either case, the human being feels uncomfortable.
To avoid this heat transfer, those portions from where the driver holds the vehicle are covered with heat insulators such as plastic, rubber or cotton.
Thus, the driver is saved from cold or heat being felt in his hands.
Question 18.
Why metals like copper, iron, brass etc. are good conductors of heat whereas wood, cardboard, ply are not conductors of heat?
Answer:
Heat conductibility in solids apart from temperature depends on the availability of conducting particles i.e. free electrons. In metals like copper, brass and iron-free electrons are available but in insulators like wood, cardboard and ply free electrons are not available, so metal is good conductors of heat.
Question 19.
House in Rajasthan made of stone and lime are cooler than those made of brick and cement why?
Answer:
The thermal conductivity of lime is smaller than that of cement. Even though stone tends to be Rotter than a brick in the day time as much as. does the cement plaster. Similarly, on cold days or cold nights even during summer, the heat of the house is not allowed to escape out. The thickness of stone walls compared to brick walls is yet another factor in keeping the houses, cool or warm in opposite”conditions.
Question 20.
Housing on hills are either made of wood or have wooden lining and walls. Why? Why people in plains where temperature variations are extreme winter and summer do not use-wooden house?
Answer:
On hills, people make wooden houses or put wooden lining, on house walls to insulate the house from the extreme cold of winter because wood being a bad conductor of heat does not allow the heat of house to escape out or exchange low outside temperature with the high temperature inside.
In plains even though wooden houses are helpful in fulfilling the odd weather conditions yet because of other factors such as
- non-availability of plenty of wood and
- chances of catching fire etc. wooden houses are generally not built.
Question 21.
People who own cars know well if they close all glass windows of the car park it in the Sun, it remains very hot inside the car even after sunset. To keep inside the car cooler insulating screens are put inside the car covering, the winds screen and curtains are pulled on the glass of windows, explain.
Answer:
Glass at normal temperature say up to 100° is opaque to heat radiations. But if radiations are coming from a source having a high temperature (surface temperature of sun ~ 6000k), it becomes transparent. Thus heat from the sun enters the car but radiations from the car being at a lower temperature (~ 50°C) cannot escape out so it remains hot, glass is opaque for radiations at such low temperature and the car body is double-walled or lined with insulators also does not allow the inner body heat to escape, Thus inside of the car remains hot.
But when screen and curtains are put the solar radiations are either reflected back or get absorbed and the temperature inside the car does not rise too much. It remains bearable.
Question 22.
What are the various properties of a thermometric substance?
Answer:
Following are the properties of a thermometric substance:
- They should have a high boiling point and low freezing point to provide for the measurement of a wide range of temperature.
- It should not be volatile.
- It should be a variable in abundance.
- Its rate of expansion should be uniform so that the calibration becomes easier.
- The coefficient of expansion of the substance should be high so that the thermometer may be sensitive.
- It should be available in a pure state.
- It should not stick to the side of the glass tube.
- It should have good thermal conductivity.
Question 23.
It is generally very cold after the hail storm than during or before it. Why?
Answer:
After a hail storm, the ice balls melt by absorbing a lot of heat energy from the atmosphere, thus reducing its temperature. Hence there is very cold after the hail storm.
Question 24.
Why pendulums made of invar are used in clocks?
Answer:
Invar has a low value of the coefficient of linear expansion, so the length of the pendulum almost remains the same in different seasons and hence gives the correct time.
Question 25.
Should a thermometer bulb have a large heat capacity or a small heat capacity? Why?
Answer:
A thermometer bulb should have a small heat capacity. In case, if it has a large capacity, the temperature of the substance will get lowered due to a large amount of heat absorbed by the thermometer bulb.
Question 26.
Explain why the coefficient of cubical expansion of water is negative between 0°C and 4°C?
Answer:
This is because of the fact that the volume of water decreases between 0°C and 4°C and water contracts within this range of temperature.
Question 27.
Why good conductors of electricity are also good conductors of heat?
Answer:
Both thermal and electrical conductivity depends upon the number of free electrons which are in large number in good conductors of electricity.
Question 28.
How is a gas thermometer better than a mercury thermometer?
Answer:
A gas thermometer is better because it can measure very low and very high temperature while the range of mercury thermometer is limited due to its freezing point – 37°C and boiling point 357°C.
Question 29.
A vertical glass jar is filled with water at 10°C. It has one thermometer at the top and another at the bottom. The central region of the jar is gradually cooled. It is found that the bottom thermometer reads 4°C earlier than the top thermometer and the top thermometer reads 0°C earlier than the bottom thermometer. Why?
Answer:
This is because water expands on cooling from 4°C to 0°C, thus it becomes of highest density at 4°C and then its density goes down. So the bottom thermometer reads 4°C earlier as the temperature of water at the top will be more than 4°C.
Question 30.
Two spheres are m&de of the same metal and have the same mass. One is solid and the other is hollow. They are heated to the same temperature. What is the percentage increase in their diameters?
Answer:
It will be the same We both spheres as the expansion of solid is like photographic enlargement, so \(\frac{\Delta \mathrm{V}}{\mathrm{V}}\) = γΔθ.
Question 31.
Nam the effects produced by the heat given to a body.
Answer:
The following are the effects produced by the heat:
- It changes the temperature of the body.
- It changes the volume of the body.
- It changes the state of the body.
- It changes the physical and chemical properties of the body.
- It produces light.
- It generates electricity.
Thermal Properties of Matter Important Extra Questions Long Answer Type
Question 1.
(a) Define the following:
(i) Coefficient of linear expansion (α)
Answer:
α – It is defined as the change in the length per unit original length per unit change in temperature of the material of a solid rod.
i.e. α = \(\frac{\Delta l}{l_{0} \Delta \mathrm{T}}\)
(ii) Coefficient of superficial expansion (β)
Answer:
β – It is defined as the change in surface area per unit original surface area per unit change in the temperature of the material of the solid.
i.e. β = \(\frac{\Delta S}{S_{0} \Delta \mathrm{T}}\)
(iii) Coefficient of cubical expansion (γ)
Answer:
γ – It is defined as the change in volume per unit original volume per unit change in the temperature of the material of the solid.
γ = \(\frac{\Delta V}{V_{0} \Delta \mathrm{T}}\)
(b) Derive the relation α, β and γ.
Answer:
Relation between α and β
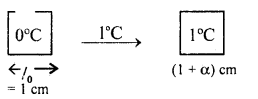
Consider a solid of length 1 cm at 0°C. Heat it by 1°C. If l0, lt be its length at 0°C and 1°C respectively, then
lo = 1 cm
and
l1 = l0 + lo ∝ Δt
= 1 + 1 × α × 1
= (1 + α) (∵ Δt = 1 – 0 = 1°C)
If So and St be its area at 0°C and 1°C respectively, then
So = lo2= 1 cm2
St = l12 = (1 + α)2 cm2
∴ ΔS = St – So = (1 + α)2 – 1
∴ By definition ,
β = \(\frac{\Delta \mathrm{S}}{\mathrm{S}_{0} \Delta \mathrm{T}}=\frac{(1+\alpha)^{2}-1}{1 \times 1}\)
= 1 + α2 + 2α – 1 = α2 + 2α
= 2α
(∵ α is very small, so α2 is neglected)
or
α = \(\frac{\beta}{2}\) …(1)
Relation between α and γ:
Consider a cube of side 1 cm at 0°C. Heat it by 1°C
∴ lo = 1 cm
and l1 = lo(1 + α Δt) = 1(1 + α × 1)
= (1 + α) cm
If Vo and Vt be its volumes at 0°C and 1°C respectively.
Then Vo = lo3 = 1 cm3
and Vt = lt3 = (1 + α)3
= 1 + α3 + 3α(1 + α)
= 1 + α3 + 3α + 3α2
= 1 + 3α
(∵ α is very small so square and higher powers are neglected.)
ΔV change in its volume, then
ΔV = Vt – Vo = 1 + 3α – l = 3α
∴ By definition,
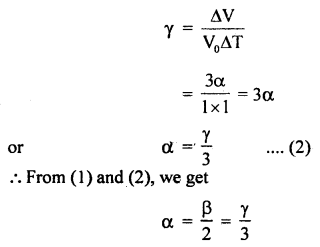
Numerical Problems:
Question 1.
Calculate the increase in the temperature of the water which falls from a height of 100 m. Assume that 90% of the energy due to fall is converted into heat and is retained by water. J = 4.2 J cal-1.
Answer:
Here, h = 100 m
Let m (kg) = mass of water
∴ Its P.E. at a height h = mgh
Energy of fall retained by water i.e. useful work done is given by,
W = 90% of mgh
= \(\frac{90}{100}\) mgh
= \(\frac{90}{100}\) × m × 9.8 × 100
= 882 m J.
∴ Heat retained, Q = \(\frac{W}{J}=\frac{m \times 882 J}{4.2 J c a l^{-1}}\)
= m × 210 cal …(i)
Specific heat of water C = 10 cal kg-1 °C-1
Let Δθ (°C) be the rise in the temperature of water.
∴ Heat gained, Q = mCΔθ
.= m × 103 × Δθ
= m × Δθ × 103 cal …. (ii)
∴ From (1) and (ii), we get
m × 210 = m × Δθ × 103
or
Δθ = \(\frac{210}{10^{3}}\)= 0.21°C.
Question 2.
A clock with a steel pendulum has a time period of 2s at 20°C. If the temperature of the clock rises to 30°C, what will be the gain or loss per day? The coefficient of linear expansion of steel is
1.2 × 10-5 C-1
Answer:
Here α = 1.2 × 10-1 °C-1
Δt = 30 – 20= 10°C
T = 2s.
Using the relation, Δl = l α Δt, we get
\(\frac{\Delta l}{l}\) = α Δt
= 1.2 × 10-5 × 10 = 1.2 × 10-4 …. (i)
∴ T = 2π \(\sqrt{\frac{l}{g}}\) ….(ii)
If T’ be the time period of the pendulum, when l increases by Δl, then
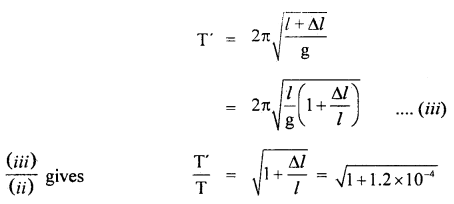
∴ loss in time in one oscillation T’ – T
Hence loss in time in one day is given by
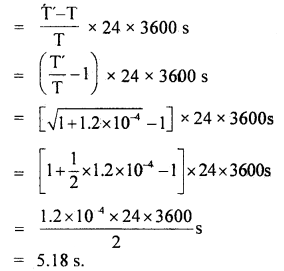
Question 3.
The thermal conductivity of brick is 1.7 W m-1 K-1 and that – of cement is 2.9 W m-1 K-1. What thickness of cement will have the same insulation as the brick of thickness 20 cm.
Answer:
Here, KB = 1.7 W m-1 K-1
KC = 2.9 W m-1 K-1
dB = 20 cm
dc = ?
We know that the heat flow is given by
Q = KA \(\frac{\Delta \theta}{\mathrm{d}}\) t
For the same insulation by the brick and the cement, Q, A, Δθ and t don’t change
Thus \(\frac{K}{d}\) should be a constant.
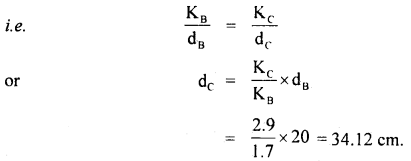
Question 4.
Two metal cubes A and B of the same size are arranged as shown in the figure. The extreme ends of the combination are maintained at the indicated temperatures. The arrangement is thermally insulated. The coefficient of thermal conductivity of A and B are 300 W/m°C and 200 W/m°C respectively. After a steady-state is reached, what will be the temperature of the interface?
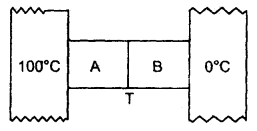
Answer:
Let T (°C) be the temperature of the interface =?
Here, K1 = 300 Wm-1 °C-1 for A
K2 = 200 Wm-1 °C-1 for B
∴ Δθ1 = 100 – T for A
Δθ2 = T – 0 for B .
x = size of each cube A and B
∴ x1 = x2 = x
Let a = area of cross-section of the faces between which there is the flow of heat
If \(\left(\frac{\Delta \mathrm{Q}_{1}}{\Delta \mathrm{t}}\right)_{\mathrm{A}}\) and \(\left(\frac{\Delta \mathrm{Q}_{2}}{\Delta \mathrm{t}}\right)_{\mathrm{B}}\) be the rate of.tlow of heat for A and B respectively, then in steady state,

Question 5.
The heat of combustion of ethane gas is 373 Kcal per mole. Assuming that 50% of heat is lost, how many litres of ethane measured at STP must be burnt to convert 50 kg of water at 10°G to steam at 100°C? One mole of gas occupies 22.4 litres at S.T.P. Latent heat (L) of steam = 2.25 × 106 JK-1.
Answer:
Here
L = 2.25 × 106 JK-1
= \(\frac{2.25}{4.2}\) × 106 cal°C-1
Q = Heat of Combustion
= 373 × 103 Cal/mole
C = 103 J Kg-1 °C-1
m = 50 kg
Δθ = 100- 10 = 90°C
V = 22.4 litres
If Q1 = Total heat energy required to convert 50 kg of water at 10°C to steam at 100°C
Q1 = mCΔθ + mL
= 5.0 × 1000 × 90 + 50 ×\(\frac{2.25 \times 10^{6}}{4.2}\)
= 4.5 × 106 + 26.79 × 106
= 31.29 × 106 cal
As 50% of heat is lost,
∴ total heat produced = \(\frac{100}{50}\) × 3.129 × 106
Let n = no. of moles of ethane to be burnt, then
n = \(\frac{2 \times 31.29 \times 10^{6}}{373 \times 10^{3}}\) mole
∴ Volume of ethane = nV
= \(\frac{2 \times 31.29 \times 10^{6}}{373 \times 10^{3}}\) × 22.4 litres
= 3758.2 litres.
Question 6.
Calculate the heat of combustion of coal when 10 g of coal on burning raises the temperature of 2 litres of water from 20°C to 55°C.
Answer:
Here, C = 1 cal g-1 °C-1
m = 2 × 103 g
Δθ = 55 – 20 = 35°C
M = 10g
If Q be the heat produced, then
Q = mCΔθ
= 2 × 103 × 1 × 35
= 70 × 103 cal
∴ If Q1 be the heat of combustion, then
Q1 = \(\frac{Q}{M}=\frac{70 \times 10^{3}}{10}\) = 7000 cal g-1
Question 7.
Calculate two specific heats of a gas from the following data:
γ = \(\frac{\mathbf{C}_{\mathrm{P}}}{\mathbf{C}_{\mathbf{v}}}\) = 1.51, density of gas at NTP = 1.234 g litre J = 4.2 × 107 erg cal-1.
Answer:
\(\frac{\mathbf{C}_{\mathrm{P}}}{\mathbf{C}_{\mathbf{v}}}\) = 1.51
P = 1.013 × 106 dyne cm-2
T= 273K
ρ = 1.234 g litre-1
m = 1 g
∴ V = \(\frac{\mathrm{m}}{\rho}=\frac{1}{1.234}\) litre
= \(\frac{1}{1.234 \times 10^{-3}}\)
Also we know that for 1g gas,
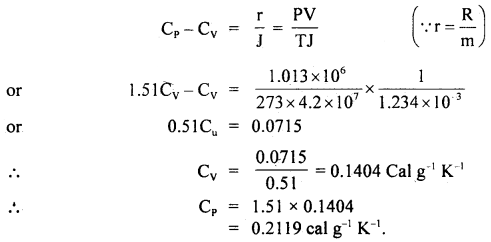
Question 8.
Specific heats of argon at constant pressure and volume are 0.125 cal g-1 and 0.075 cal g-1 respectively. Calculate the density of argon at N.T.P. (J = 4.18 × 107 ergs/cal and normal pressure = 1.01 × 106 dynes cm-2.)
Answer:
Here, CP = 0.125 cal g-1
Cv = 0.075 cal g-1 J
J = 4.18 × 107 ergs cal-1
P = 1.01 × 106 dyne cm-2
d = density at NTP = ?
m = 1 g
T = 273 K
Using the relation,
Cp – Cv = \(\frac{r}{J}=\frac{P V}{T J}=\frac{P m}{d T J}\) (∵ V = \(\frac{m}{d}\))
d = \(\frac{P m}{\mathrm{~TJ}\left(\mathrm{C}_{r}-\mathrm{C}_{\mathrm{v}}\right)}\)
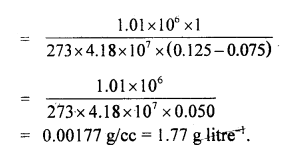
Question 9.
A piece of metal weighs 46 g in air. When it is immersed ¡n a liquid of specific gravity 124 at 27°C, it weighs 30g. When the temperature of the liquid is raised to42°C, the metal piece weighs 30.5 g. The specific gravity of the liquid at 42°C ¡s 1.20. Calculate the coefficient of linear expansion of the metal.
Answer:
Here, the Weight of the metal piece at 27°C in air 46 g
Weight of metal piece at 27°C in liquid =30 g
Weight of metal piece at 42°C in liquid = 30.5 g
α =?
Loss in weight of the metal = weight of liqiid displaced = 46 – 30
= 16 g.
The volume of metal at 27°C = Volume of liquid displaced at 27°C
or
V1 = \(\frac{16 g}{\text { specific gravity of liquid }}\)
= \(\frac{16 \mathrm{~g}}{1.24 \mathrm{gcm}^{-3}}\)
= 12.903 cm3
Similarly volume of metal piece at 42°C = V2 = \(\frac{(46-30.5)}{1.2 \mathrm{gcm}^{-3}}\)
= 12.917 cm3
∴ Coefficient of cubical expansion of the metal
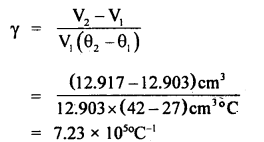
Since γ = 3α
∴ α = \(\frac{1}{3}\) γ = \(\frac{1}{3}\) × 2.41 × 105 °C-1
= 0.803 × 105 °C-1
Question 10.
In an industrial process, 10 kg of water per hour is to be heated from 20°C to 80°C. To do so, steam at 150°C is passed from a boiler into a copper coil immersed in water. The steam condenses in the coil and is returned to the boiler as water at 90°C. How many kg of steam is required per hour? Specific heat of steam = 1 Kcal kg-1 °C-1 and latent heat of steam = 540 Kcal kg-1.
Answer:
C = sp. heat of steam
= 1 Kcal kg-1 °c-1
L = latent heat of steam
= 540 Kcal kg-1
Let m (kg) = mass of steam required per hour.
Heat is given by steam first from 150°C to steam at 100°C = mCΔθ
= m × (150 – 100)Kcal = 50 m Kcal.
Then steam changes from steam at 100°C to water at 100°C and gives out heat = mL = 540 m Kcal.
After this water at 100°C gives heat is going to temperature 90°C = m (100 – 90) = 10m Kcal.
Total amount of heat given by the steam = 50 m + 540 m + 10 m = 600 m Kcal.
∴ 600 m K cal = 600 K cal
∴ m = 1 kilogram.
Question 11.
An electric heater is used in a room with a total wall area of 137 m2 to maintain a temperature of +20°C inside it when the outside temperature is -10°C. The wall has three layers of different materials. The innermost layer is of wood of thickness 2.5 cm, the middle layer is of cement of thickness 1.0 cm and the outermost layer is of brick of thickness 25.0 cm. Find the power of the electric heater. Assume that there is no heat loss through the floor and ceiling. The thermal conductivity of wood, cement and brick are 0. 125,1.5 and 1.0 Wm-1 °C-1 respectively.
Answer:
Let the temperature inside the room be θ1, at the interface of wood and cement be θ2, at the interface of cement and brick θ3 respectively. The outside temperature is θ4.
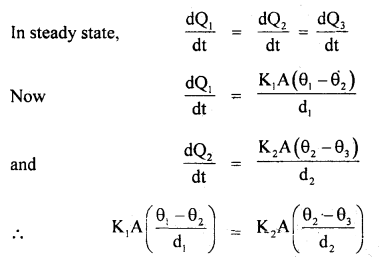
Here, K1 = 0.125 Wm-1 °C, K2 = 1.5 Wm-1 °C-1, K3 = 1.0 Wm-1 °C-1 A = 137m2 , θ1 = 20°C θ4 = -10°C , d1 = 2.5 cm, d2 = 1.0 cm, d3 = 25 cm.
∴ \(\frac{0.125\left(20-\theta_{2}\right)}{2.5}=\frac{1.5\left(\theta_{2}-\theta_{3}\right)}{1}\)
or
5(20 – θ2) = 150(θ2 – θ3)
or
20 – θ2 = 30(θ2 – θ3) ,
or
20 = 31θ2 – 30θ3
Similarly from
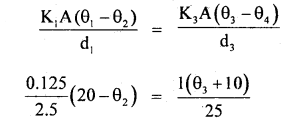
or
20 – θ2 = \(\frac{4}{5}\) (θ3 + 10)
or
θ3 = \(\frac{5}{4}\) (20 – θ2) – 10 …(2)
∴ From (1) and (2), we get
20 = 3lθ2 – 30 × (20 – θ2) + 30 × 10
or
80 = 124θ2 – 150(20 – θ2)+ 1200
= 274θ2 – 3000 + 1200
or
274θ2 = 18800
∴ θ2 = \(\frac{940}{137}\) °C
∴ If P be the heater power, then
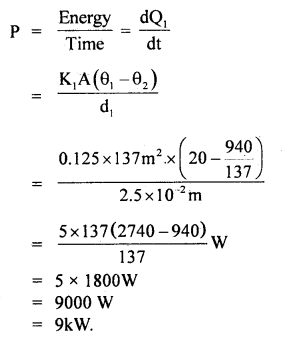
Question 12.
The opposite faces of a cubical block of iron of cross-section 4 cm2 are kept in contact with steam and melting ice. Calculate the amount of ice melted at the end of 10 minutes if K = 0.2 cal cm-1 s-1 °C-1 for iron. Latent heat of fusion of ice = 80 cal g-1.
Answer:
Here, L = latent heat of ice
= 80 cal g-1
A = 4 cm2 .
K = 0.2 cal cm-1 s-1 °C-1
Δθ = θ2 – θ1 = 100 – 0 = 100°C
t = time = 10 minutes = 10 × 60 = 600s
d = \(\sqrt{4}\) =2 cm
Let m = amount of ice melted = ?
Using the relation, Q = \(\frac{\mathrm{K} \mathrm{A}\left(\theta_{2}-\theta_{1}\right) \mathrm{t}}{\mathrm{d}}\), we get
Q = \(\frac{0.2 \times 4 \times 100 \times 600}{2}\)
Q = 24000 cal …(i)
Also, Q = mL = m. 80 …(ii)
∴ From (i) and (ii), we get
m × 80 = 24000
∴ m = \(\frac{24000}{80}\) = 300 g.
Question 13.
Water is boiled in a rectangular steel tank of thickness 2 cm by a constant temperature furnace. Due to vaporisation, the water level falls at a steady rate of 1 cm in 9 minutes. Calculate the temperature of the furnace. Given the thermal conductivity of steel is 0.2 cal cm-1 s-1 °C-1 and latent heat of steam is 540 cal.
Answer:
d = 2 cm
t = 9 minutes = 9 × 60 = 540 s
K = 0.2 cal cm-1 s-1 °C-1
L = 540 cal.
Let A be the area of the bottom of the steel tank.
θ1 = temperature of the tank which is in contact with the constant temperature furnace?
fall in level of water = 1cm
∴ volume of water evaporated, V = A × 1 = A cm3
ρ = density of water = 1 g/cm3
Mass of water evaporated, m = ρV – 1 × A = Ag .
Q = heat required to evaporate Ag of water in 9 minute = A × 540 cal.
Also, Q = \(\frac{\mathrm{KA}\left(\theta_{\mathrm{1}}-\theta_{2}\right) \mathrm{t}}{\mathrm{d}}\)
or
540A = \(\frac{0.2 \mathrm{~A} \times\left(\theta_{1}-\theta_{2}\right) 540}{2}\)
or
θ1 – θ2 = \(\frac{2}{0.2}\) = 10
Here, θ2 = 100°C
θ1 = θ2 + 10 = 100 + 10= 110 °C.
Question 14.
A circular hole of a radius of 1 cm is drilled in a brass sheet kept at 293K. What will be the diameter of the hole when the sheet is heated to 393K? a for brass = 18 × 10-6 K-1.
Answer:
Here, α = 18 × 10-6 K-1
ΔT = 393 – 293 K = 100 K
r = radius = 1 cm
∴ D = 2r = diameter = 2 cm
and it acts as the original length l (say).
∴ Let D’ be the new diameter = ?
I f Δl be the increase in length, then using the relation,
Δl = αlΔt, we get
Δl = 18 × 10-6 × 2 × 100 = 36 × 10-4 cm
∴ increase in diameter, AD = Al = 36 × 10-4 cm
∴ D’ = D + ΔD = 2 + 0.0036 = 2.0036cm.
Question 15.
Find the change in the length of the steel bridge of the original length of 200 m in a locality where temperature changes from 243 to 313K. a for steel = 11 × 10-6 K-1.
Answer:
Here, T1 = 243 K
T2 = 313 K
∴ ΔT = change in temperature
= T2 – T1 = 313 – 243 = 70 K
l = 200 m
α = 11 × 10-6 K-1
Let Δl = change in the length of the bridge = ?
∴ Δl = lα ΔT
= 200 × 11 × 10-6 × 70
= 154 × 10-3 m
= 0.154 m = 15.4 cm.
Question 16.
Equal volumes of copper and mercury have the same thermal capacity. Mercury has a specific heat of0.046 and a density of 13.6 g cm-3. Calculate the density of copper having sp. heat 0.092.
Answer:
Let C1 and C2 be the sp. heat of mercury and copper respectively having densities ρ1 and ρ2
Here, ρ1 = 13.6 g cm-3
C1 = 0.046
C2 = 0.092
∴ ρ2 =?
Let V = volume of copper and mercury.
If m1 and m2 be the mass of mercury and copper, then
m1 = V × ρ1
and
m2 = V × ρ2
Also let H1 and H2 be their respective thermal capacity, so using
Thermal capacity = mass × sp. heat, we get
H1 = Vρ1 × C1
and
H2 = Vρ2 × C2
As H1 = H2
Vρ1C1 = Vρ2C2
or
ρ2 = ρ1\(\frac{C_{1}}{C_{2}}=\frac{13.6 \times 0.046}{0.092}\)
= 6.8gcm3.
Question 17.
What would be the final temperature of the mixture when 5 g of ice at -10°C is mixed with 20 g of water at 30°C? Sp. the heat of ice is 0.5 and latent heat of water – 80 cal g-1.
Answer:
Here, m1 = mass of water = 20 g
θ1 = temperature of water = 30°C
θ2 = temperature of ice = -10°C
C1 = sp. heat of waterr = 1
C2 = sp, heat of ice.= 0.5
m2 = mass of ice = 5 g
Let θ = final temperatre of the mixture
L = latent heat of water = 80 cal g-1
∴ Heat lost by water is given by
H1 = 20 × 1 × (30 – θ) ….(1)
(∵ H = mCΔθ)
Heat required to raise 5 g of ice at -10°C to 0°C
H2 = 5 × [0 – (-10)] × 0.5
= 5 × 10 × \(\frac{5}{10}\) = 25 cal ….(2)
Let H3 = heat required to meet 5 g of ice at 0°C to water at 0°C
H3 = m2L
= 5 × 80 = 400 cal ….(3)
Also let H4 = heat required to raise 5 g of water at 0°C to θ°C
∴ H4 = 5 × 1 × θ = 5θ
∴ Total heat gained by ice = H2 + H3 + H4
= 25 + 400 + 5θ
∴ Heat lost = Heat gained gives
20(30 – θ) = 425 + 5θ
or
600 – 200 = 425 + 5θ
or
600 – 425 = (20 + 5)θ
or
25θ = 175
∴ θ = \(\frac{175}{25}\) = 7 °C.
Question 18.
A faulty Celcius thermometer has lower and upper fixed points as 1°C and 101°C; it reads a certain temperature as 50°C. What is the correct temperature?
Answer:
Let Correct temp. = x°C
∴ \(\frac{x-0}{100-0}=\frac{50-1}{101-1}\)
or
\(\frac{x}{100}=\frac{49}{100}\)
or
x = 49°C.
Question 19.
At what temperature do the Celsius and Fahrenheit readings have the same numerical value?
Answer:
Let x be the required value in °C and °F.
i.e. tF = tc = x°
∴ Using the relation, \(\frac{\mathbf{C}-0}{100}=\frac{\mathrm{F}-32}{180}\), we get
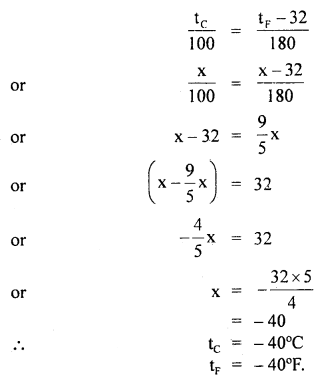
Question 20.
At what temperature do the Kelvin and Fahrenheit readings have the same numerical value?
Answer:
Let x be the required value in °K and °F
tK = tF = x
Using the relation,
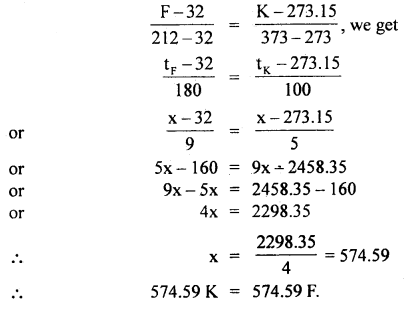
Question 21.
Express 37°C into Farenheit.
Answer:
Here, tc = 37°C
tF = ?
Using the relation, \(\frac{C-0}{100}=\frac{F-32}{180}\) we get
or
F – 32 = \(\frac{9}{5}\) × C
∴ F = \(\frac{9}{5}\)C + 32
= \(\frac{9}{5}\) × 37+32
= 66.6 + 32
= 98.6°F.
Question 22.
The temperature of a body is increased from 100°F to 910°F. What is the temperature range in the Kélvin scale?
Answer:
Here, Δt = (T2 — T1)°F
= 910 – 100°F
= 810°F
Using the relation, ΔC = \(\frac{5}{9}\) × ΔF
or
ΔC = \(\frac{5}{9}\) × 810 – 450
∴ ΔC = 450°K
Question 23.
A faulty thermometer has its fixed points marked as 50 and 95°. When it reads 590 what is the corresponding temperature in °C?
Answer:
Let x be the reading ¡n °C.
∴ \(\frac{x-0}{100-0}=\frac{59-5}{95-5}\)
or
\(\frac{x}{100}=\frac{54}{90}=\frac{3}{5}\)
or
x = \(\frac{3}{5}\) × 100 = 60°C.
Question 24.
The temperature coefficient of resistance of a Wire is 0.00125 per °C. At 300 K its resistance is 1 Q. At what temperature will the resistance of the wire be 2Ω?
Answer:
Here, α = 125 × 105 °C-1
R300 = 1Ω
Let Rθ be its resistance at θ°C
∴ Rθ = 2Ω
∴ Δθ = rise in its temp.
∴ Using the relation
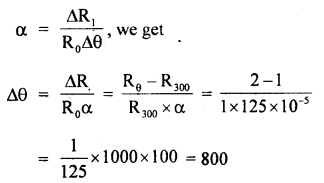
or
θ – 300 = 800
∴ θ = 800 + 300 = 1100 K
Question 25.
Calculate the temperature difference in °F equivalent to temperature difference of 25°C.
Answer:
Here, ΔC = 25°C
ΔF =?
Using the relation, ΔF = \(\frac{9}{5}\) × ΔC, we get
ΔF = \(\frac{9}{5}\) × 25
= 45°F.
Value-Based Type:
Question 1.
Venkat having found his mother suffering from fever Venkat took her to the doctor for treatment. While checking the status, the doctor used a thermometer to know the temperature of the body. He kept the thermometer in the mouth of the patient and noted the reading as 102°F. The doctor gave the necessary medicines. After coming home, Venkat asked his mother, who Is a science teacher, why mercury is used in a thermometer when there are so many liquids. Then his mother explained the reason.
(a) Comment upon the values of the mother.
Answer:
Mother has an interest in educating her son and explained that Mercury has got the following properties for being used in their- monitors
- The expansion of Mercury is fairly regular and uniform.
- It is opaque and shining, hence can be easily seen through the glass tube.
- Mercury is a good conductor of heat and has a low thermal capacity,
- Mercury dose is not wet on the sides of the glass tube in which it is tilled.
(b) A newly designed thermometer has its lower fixed point and upper, the fixed point marked at 5° and 95° respectively. Compute the temperature on this scale corresponding to 50°C.
Answer:
Let θ be the temperature on the scale corresponding to θ = 50°C.
Then \(\frac{\theta-5}{95-5}=\frac{C-0}{100-0}=\frac{C}{100}\)
or
θ = 50°
Thus, the required temperature on the scale of the designed ther¬mometer is 50°.
Question 2.
Raman noticed that his grandfather to be suffering from fever. He took him to the doctor. The doctor gave him some pills. When the pills were used he sweated much, after some time became normal. Rahim enquired the Doctor about how his grandfather become normal.
(a) According to you what values are possessed by Raman?
Answer:
Raman is responsible and he has concern for others, inquisitiveness in gaining knowledge, curiosity
(b) A child running a temperature of 101°Fis given an Antipyrin which causes an increase in the rate of evaporation of the body. If the fever is brought down to 98° F in 20 m, what is the amount of heat lost by the body? The mass of the child is 30 kg.
Answer:
Loss in temperature (Dt) =101°F – 98°F = 3°F = 3 × \(\frac{5}{9}\) °C
= 1.67 °C
Specific heat of water (S) = 1000 Gal. kg-1 °C-1
m = 30 kg
∴ Heat lost by the body = ms Δt
= 30kg × 1000 Cal. kg-1 °C-1 × 1.67°C
=501000 Cal
Question 3.
Radha and Kavita are two friends of science stream. They were discussing the phenomena of cooling. Radha told that a hot body will lose its temperature more rapidly in a room where the temperature would be less. Kavita did a small activity by putting two j glasses having the same temperature in two different room of different room temperature and note down the temperature after 10 min. She found that Radha’s idea was correct.
(i) What values are exhibited by Kavita?
Answer:
Kavita’s values are:
Curiosity, Interested in the experiment. Habit to check the correctness of an idea.
(ii) Write the law relating to this phenomena.
Solution:
The rate of loss of heat depends on the difference in temperature between the body and its surroundings. Newton was the first to study.
According to Newton’s law of cooling, the rate of loss of heat (-dQ/dt) of the body is directly proportional 1o the difference of temperature DT = (T2– T1) of the body and the surrounding. The law holds goods only for the small difference in temperature.
i.e – \(\frac{dQ}{dt}\) = K(T2 – T1)
-ve sign implies that as time passes, temperature (T) decreases.
Question 4.
Anurag and Akash were discussing heat transfer. Anurag told that houses of concrete roofs get very hot during summer days because the thermal conductivity of concrete (though much smaller than that of metal) is still not small enough. Therefore, people usually prefer to give a layer of earth or foam insulation on the ceiling so that heat transfer is prohibited and keeps the room cooler. But Akash was not convinced by this idea. He told me that it is just to decorate the ceiling.
(i) What values are displayed by Anurag?
Answer:
Application of scientific reason, curiosity, the attitude of group discussion and problem-solving skill.
(ii) Whether Anurag was telling right or wrong?
Answer:
Yes, Anurag was telling right.
(iii) On what factors the amount of heat flowing from the hot face to the cold face depends?
Answer:
Heat flowing Q α A; A = Cross-sectional area
α Δθ ; Δθ = Temperature difference
α t ; t = time
α 1/Δx; Δx = Distance between the two face
On combining the above relations, we get.
i.e Q = \(\frac{\mathrm{KA} \Delta \theta}{\Delta x}\) t
Where K is the proportionality constant known as the coefficient of thermal conductivity