Students can access the CBSE Sample Papers for Class 10 Maths with Solutions and marking scheme Term 2 Set 4 will help students in understanding the difficulty level of the exam.
CBSE Sample Papers for Class 10 Maths Standard Term 2 Set 4 with Solutions
Time : 2 Hr.
Max. Marks : 40
General Instructions :
- The question paper consists of 14 questions divided into three Sections A, B, C.
- All questions are compulsory.
- Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
- Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
- Section C comprises of 4 questions of 4 marks each. An internal choice has been provided in one question. It contains two case study based questions.
Section – A
Question 1.
In the given figure, XP and XQ are two tangents to the circle with centre O drawn from an external point X. ARB is another tangent touching the circle at R. Prove that XA + AR = XB + BR. (2)
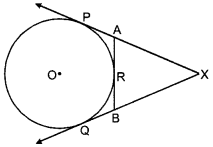
Prove that the tangents drawn at the end of any diameter are parallel.
Answer:
As XP and XQ are two tangents from X, so
XP = XQ ………….(i)
AP = AR ………….(ii) [Tangents from the external point A]
and BR = BQ [Tangents from the external point B] …(iii)
Now, XP = XQ [from (i)]
⇒ XA + AP =XB±BQ
⇒ XA + AR = XB + BR [from (ii) and (iii)]
OR
As AC and DF are tangents to B and E, the opposite points of the diameter BE.
∴ ∠ABO = ∠OBC = ∠DEO – ∠OEF=90° [the tangent at a point is always perpendicular to the radius at that point]
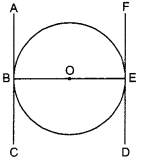
Hence, ∠ABO = ∠OED,
which are alternate interior angles.
∴ AC || DF.
Question 2.
For what value of p are 2p + 1, 13, 5p – 3 are the three consecutive terms of an A.P. ? (2)
Answer:
For 2p + 1, 13, 5p – 3 to be consecutive, the common difference should be the same.
Thus 13 – (2p + 1) = 5p – 3 – 13
⇒ 12p – 2p = 5p – 16
⇒ 7p = 28
⇒ p = 4
Question 3.
Solve : abx2 + (b2 – ac)x – bc = 0. (2)
Answer:
Given,
abx2 + (b2 – ac)x – bc = 0
⇒ abx2 + b2x – acx – bc = 0
⇒ bx(ax + b) – c(ax + b) = 0
⇒ (ax + b) (bx – c) = 0
⇒ x = \(\frac {-b}{a}\) and \(\frac {c}{b}\)
Question 4.
Two types of water tankers are available in a shop. One is in a cubic form of dimensions lmxlmxlm and another is in the cylindrical form of height 1 m and diameter 1 m. Calculate the volume of both the containers. (Use π = 3.14) (2)
Answer:
∴ Dimensions of cubic tank, l = 1 m, b = 1 m, h = 1 m
Volume of cubic tank = lbh = 1 × 1 × 1 = 1 m3
Height of cylindrical container = 1 m
Radius = \(\frac {1}{2}\) m
∴ Volume of cylindrical tank = πr2h
= \(3.14 \times \frac{1}{2} \times \frac{1}{2} \times 1\)
= 0.785 m3.
Question 5.
Find the mode of the following frequency distribution : (2)
| Class Interval | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 |
| Frequency | 2 | 8 | 10 | 5 | 4 | 3 |
Answer:
| Class Interval | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | |
| Frequency | 2 | 8 | 10 | 5 | 4 | 3 | N = 32 |
Since, 20—30 has the highest frequency, it is the modal class.
So, l = 120, f = 10, f1 = 8, f2 = 5, h = 10
Thus, Mode = \(l+\frac{f-f_{1}}{2 f-f_{1}-f_{2}} \times h\)
= \(20+\frac{10-8}{20-8-5} \times 10\)
= 20 + \(\frac {2}{7}\) x 10
= 20 + 2.86
= 22.86.
Question 6.
Find the number of natural numbers between 101 and 999 which are divisible by both 2 and 5. (2)
Answer:
As the numbers that are divisible by both 2 and 5, have their last digits as always 0. Hence, the series is 110, 120, 130, …, 990.
Here, a = 110, d = 10 and tn = 990
We know that, tn = a + (n – 1)d
⇒ 990 = 110 + (n – 1)10
⇒ (n – 1)10 = 880
⇒ n – 1 = 88
⇒ n = 89
Thus, the number of natural numbers between 101 and 999 which are divisible by both 2 and 5 is 89.
Section – B
Question 7.
Find the mean and median for the following data : (3)
| Class | 0-4 | 4-8 | 8-12 | 12-16 | 16-20 |
| Frequency | 3 | 5 | 9 | 5 | 3 |
Answer:
| Class | Frequency (fi) | xi | fixi | c.fi |
| 0-4 | 3 | 2 | 6 | 3 |
| 4-8 | 5 | 6 | 30 | cf = 8 |
| 8-12 | f = 9 | 10 | 90 | 17 |
| 12-16 | 5 | 14 | 70 | 22 |
| 16-20 | 3 | 18 | 54 | 25 |
| ∑fi = 25 | ∑fixi = 250 |

Question 8.
Draw a pair of tangents to a circle of radius 4.5 cm, which are inclined to each other at an angle of 45°. (3)
Answer:
Steps of construction:
Step I: Draw a circle of radius 4.5 cm, which centre O.
Step II : Draw a radius OA.
Step III: Draw an angle LAOB of 135° i.e., (180° – 45°)
Step IV : At point A and B, draw an angle of 90°
Step V : The two lines at point A and B intersect at P.
Step VI: Then, AD and BP are the required tangents.
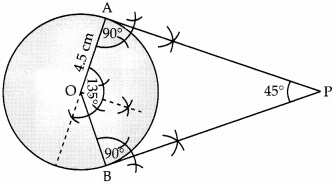
Draw,
∠AOB = 135°
∠CAP = 90°
∠OBP = 90°
∴ PA and PB are the required tangents.
Question 9.
The cumulative frequency is as shown below: (3)
| Weight | 50-60 | 60-70 | 70-80 | 80-90 | 90 -100 | 100-110 | 110-120 | 120- 30 |
| Frequency | 8 | 10 | 12 | 16 | 18 | 14 | 12 | 10 |
Calculate the cumulative frequency and determine the median class.
OR
The contents of 100 matchboxes were checked to determine the number of matchsticks they contained.
| Matchboxes | 35 | 36 | 37 | 38 | 39 | 40 | 41 |
| Matchsticks | 6 | 10 | 18 | 25 | 21 | 12 | 8 |
Calculate the mean of the number of matchsticks per box and determine how many extra matchsticks would have to be added to the total contents of the 100 boxes to bring up the mean to 39.
Answer:
The following table shows the weights (in gm) of a sample of 100 potatoes taken from a large consignment.
| Weight | Frequency | Cumulative Frequency |
| 50-60 | 8 | 8 |
| 60-70 | 10 | 18 |
| 70-80 | 12 | 30 |
| 80-90 | 16 | 46 |
| 90 – 100 | 18 | 64 |
| 100-110 | 14 | 78 |
| 110-120 | 12 | 90 |
| 120-130 | 10 | 100 |
| N = ∑fi = 100 |
Now
N = \(\mathrm{N}=\Sigma f_{i}=100\)
⇒ \(\frac{\mathrm{N}}{2}=\frac{100}{2}=50\)
The cumulative frequency just above 50 is 64.
Hence, the median class is 90 – 100.
OR
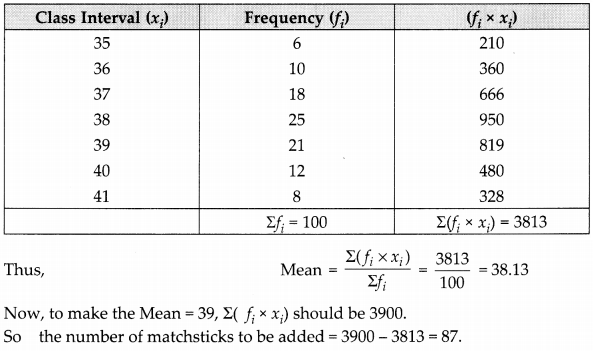
Question 10.
The angle of depression of a car standing on the ground from the top of a 75 m high tower is 30°. Find the distance of the car from the base of the tower (in m). (3)
Answer:
Let the distance of the car from the base of the tower be x m.
Height of tower = 75 m
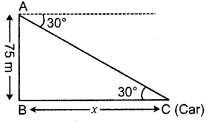
tan 30° = \(\frac {Perpendicular}{Base}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{75}{x}\)
⇒ x = \(75\sqrt{3}\)
Thus, distance of the car from the base of the tower is \(75\sqrt{3}\) m.
Question 11.
Due to heavy floods in a state, thousands were rendered homeless. 50 schools collectively offered to the state government to provide place and the canvas for 1500 tents to be fixed by the government and decided to share the whole expenditure equally. The lower part of each tent is cylindrical of base radius 2.8 m and height 3.5 m, with conical upper part of same base radius but of height 2.1 m. If the canvas used to make the tents costs ₹ 120 per sq. m, find the amount shared by each school to set-up the tents. (4)
OR
From a solid cylinder of height 15 cm and diameter 16 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid. [Take n = 3.14]
Answer:
Radius of the base of cylinder (r) = 2.8 m
Radius of the base of the cone (r) = 2.8 m
Height of the cylinder (h) = 3.5 m
Height of the cone (H) = 2.1 m
Slant height of conical part (t) = \(\)
\(\begin{aligned}
&=\sqrt{r^{2}+H^{2}} \\
&=\sqrt{(2.8)^{2}+(2.1)^{2}} \\
&=\sqrt{7.84+4.41}
\end{aligned}\)
= \(\sqrt{12.25}\)
= 3.5 m.
Area of canvas used to make tent = CSA of cylinder + CSA of cone
= 2πrh + πrln
= \(2 \times \frac{22}{7} \times 2.8 \times 3.5+\frac{22}{7} \times 2.8 \times 3.5\)
= 61.6 + 30.8
= 92.4 m2.
Cost of 1500 tents at ₹ 120 per sq. m = 1500 × 120 × 92.4
= 16,632,000
Share of each school to set-up the tents = \(\frac{16632000}{50}\)
= ₹ 332,640.
OR
Given, height of solid cylinder and cone (h) =15 cm
Diameter of cylinder and cone = 16 cm
∴ Radius of cylinder and cone (r) =8 cm
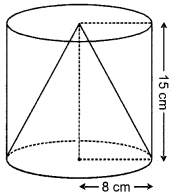
Thus, curved surface area of cylinder
= 2πrh
= 2 x π 8 x 15 cm2
= 240π cm2
and curved surface area of cone
= \(\pi(8)\left(\sqrt{(8)^{2}+(15)^{2}}\right)\) m2
= \(\pi(8)(\sqrt{64+225})\) cm2
= \(\pi(8)(\sqrt{289})\) cm2
= \(\pi(8)(17)\) cm2
= 136π cm2
and the area of the top of cylinder
= π(8)2 cm2
=64π cm2
Hence, the total surface area of the remaining solid
= 240π + 136π + 64π
= 440π cm2
= 440(3.14) cm2
= 1381.6 cm2.
Question 12.
The horizontal distance between two poles is 15 m. The angle of depression of the top of the first pole as seen from the top of the second pole is 30. 1f the height of the second pole is 24 m, find the height of the first pole. [Use √3 = 1.7321] (4)
Answer:
Let the height of the first pole be H m.
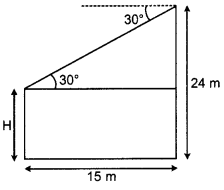
\(\tan 30^{\circ}=\frac{24-\mathrm{H}}{15}=\frac{1}{\sqrt{3}}\)
⇒ \(\sqrt{3}(24-\mathrm{H})=15\)
⇒ 24 – H = 5√3
⇒ H = 24 – 5√3
= [24 – 5(1.732)] m
= (24 – 8.66)m
= 15.34 m
So, the height of the first pole is 15.34 m.
Question 13.
Amit was playing a number card game. In the game, some number cards (having both +ve or -ve numbers) are arranged in a row such that they are following an arithmetic progression. On his first turn, Amit picks up 6th and 14th card and finds their sum to be -76. On the second turn he picks up 8th and 16th card and finds their sum to be – 96. (4)
Based on the above information, answer the following questions.
(i) What is the difference between the numbers on any two consecutive cards?
(ii) What is the sum of 9th and 15th card ?
Let the numbers on the cards be a, a + d, a + 2d, …
According to questions, we have
(a + 5d) + (a + 13d) = -76
⇒ 2a – 18d = -76
⇒ a + 9d – 38
And (a + 7d) + (a + 15d) = -96
⇒ 2a + 22d = -96
⇒ a + 11d = -48
From equations (i) and (ii), we get
24 = -10 ⇒ d = 5
(ii) From (i), a + 9(-5) = -38 ⇒ a = 7
Number on 9th card = a + 8d
= 7 + 8 x – 5
=7 – 40 = -33
Number on 15th card = a + 144
= 7 + 14 x -5
= 7 – 70
= -63
Sum of 9th and 15th card = -33 + (-63)
= 96
14. For class of 10 students, a teacher planned a game for the revision of chapter circles with some questions written on the board, which are to be answered by the students. For each correct answer, a student will get a reward. Some of the questions are given below. (4)
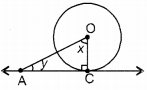
(i) In the given figure, x + y = ?
(ii) If PA and PB are two tangents drawn to a circle with centre O from P such that ∠PBA = 50°, then ∠OAB = ?
Answer:
(i) In ∆OAC, ∆OCA 900 [Since, radius at the point of contact is perpendicular to tangentj
∠OAC + ∠AOC = 90°
x + y = 90°
(ii) Since OB ⊥PB [Since, radius at the point of contact is perpendicular to tangent]
and ∠PBA = 500 (Given)
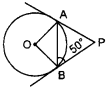
∠OBA = 90°- 50° = 40°
Also, OA = OB [Radius of circle]
∠OAB = ∠OBA = 40° [Angle opposite to equal sides are equal]