Students can access the CBSE Sample Papers for Class 10 Maths Basic with Solutions and marking scheme Set 7 will help students in understanding the difficulty level of the exam.
CBSE Sample Papers for Class 10 Maths Basic Set 7 with Solutions
Maximum Marks: 80
Time Allowed: 3 hours
General Instructions:
1. This Question Paper has 5 Sections A, B, C, D and E.
2. Section A has 20 Multiple Choice Questions (MCQs) carrying 1 mark each.
3. Section B has 5 Short Answers-I (SA-I) type questions carrying 2 marks each.
4. Section C has 6 Short Answers-IT (SA-II) type questions carrying 3 marks each
5. Section D has 4 Long Answers (LA) type questions carrying 5 marks each.
6. Section E has 3 source based/case based/passage based integrated units of assessment (4 marks each) with sub¬ parts of the values of 1,1 and 2 marks each respectively.
7. All questions are compulsory. However, an internal choice in 2 Qs of 2 marks, 2 Qs of 3 marks and 2 Qs of 5 marks has been given provided. An internal choice has been provided in 2 marks questions of Section E.
8. Draw neat figures wherever required. Take π = 22/7, wherever required if not stated.
Section – A(20 Marks)
Question 1.
a and bare two positive integers such that the least prime factor of a is 3 and the least prime factor of b is 5. Then, calculate the least prime factor of (a + b).
(A) 1
(B) 8
(C) 2
(D) 5
Solution:
(C) 2
Explanation: a and b are two positive integers such that the least prime factor of a is 3 and the least prime factor of b is 5.
Since, least prime factor of a is 3 it implies that ‘a’ is an odd number similarly b is also odd number and we know that odd + odd = even.
So, a + b = even and we know that least prime factor of any even number is always 2.
∴ The least prime factor of (a + b) is 2.
![]()
Question 2.
P and Q are two positive integers such that P = p3q and Q = (pq)2, where p and q are prime numbers. What is LCM (P, Q)?
(A) pq
(B) P2q2
(C) p3q2
(D) p5q3
Solution:
(C) p3q2
Explanation:
P = p3q
and Q = (pq)2
Then LCM (P, Q) = p3q2
Question 3.
The first term of A.P. is p and the common difference is q, then its 10th term is
(A) q + 9p
(B) p – 9q
(C) p + 9q
(D) 2p + 9q
Solution:
(C) p + 9q
Explanation: a= p and d = q (given)
∴ 10th term = a + (10 – 1)d
= p + 9q
Question 4.
What is the common difference of an A.P., in which a18 – a14 = 32?
(A) 8
(B) -8
(C) -4
(D) 4
Solution:
(A) 8
Explanation: In the given A.P., a18 – a14 = 32
Thus, a18 – a14 = 32
⇒ a + 17d – a – 13d = 32
⇒ 4d = 32
⇒ d = 8
Question 5.
The nature of roots of quadratic equation 3x2 – 6x + 1 = 0 is
(A) real and equal
(B) real and distinct
(C) not real
(D) not real and equal
Solution:
(B) real and distinct
Explanation: Given that equation is 3x2 – 6x + 1 = 0
We know that Discriminant, D = b2 – 4ac
Here on comparing a = 3, b = -6, c = 1
We have D = (-6)2 – 4(3)(1) = 36 – 12 = 24
As D > 0 so the given quadratic equation has real and distinct roots.
![]()
Question 6.
The fourth vertex D of a parallelogram ABCD whose three vertices are A (-2, 3), B (6, 7) and C (8, 3) is.
(A) (0, 1)
(B) (0, -1)
(C) (-1, 0)
(D) (1, 0)
Solution:
(B) (0, -1)
Explanation:

⇒ 6 = 6 + x4 and 6 = 7 + y4
⇒ x4 = 0 and y4 = -1
Hence, the fourth vertex of parallelogram is D(x4, y4) = (0, -1).
Question 7.
In ΔABC and ΔDEF, ∠F = ∠C, ∠B = ∠E and AB = \(\frac{1}{2}\)DE. Then the two triangles are
(A) Congruent, but not similar
(B) Similar, but not congruent
(C) Neither congruent nor similar
(D) Congruent as well as similar
Solution:
(B) Similar, but not congruent
Explanation: According to the definition of similarity of two triangles, “Two triangles are similar when their corresponding angles are equal and the sides are in proportion”
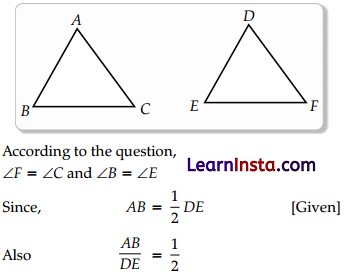
Which means the triangles are similar but not congruent.
Question 8.
In ΔABC ~ ΔDEF and ∠A = 47°, ∠E = 83°, then ∠C is equal
(A) 47°
(B) 50°
(C) 83°
(D) 130°
Solution:
(B) 50°
Explanation: We have,
In triangle ABC and DEF,
ΔABC ~ ΔDEF
∠B = ∠E = 83° … (i)
Now, in triangle ABC
∠A + ∠B + ∠C = 180° (by Angle sum property of triangle)
⇒ ∠A + ∠E + ∠C = 180° [From eq. (i)]
⇒ 47° + 83° + ∠C = 180°
⇒ ∠C = 180° – 130° = 50°
Question 9.
In the given figure, PQ is tangent to the circle with centre at O, at the point B. If ∠AOB = 100°, then ∠ABP is equal to
(A) 50°
(B) 40°
(C) 60°
(D) 80°
Solution:
(A) 50°
Explanation:
OA = OB [Radius of circle]
∠OAB = ∠OBA [Isosceles triangle property]
Now is DOAB, ∠OAB = \(\frac{180-100}{2}\) = 40 [Angle Sum property of ΔOAB]
Hence, ∠ABP = ∠OBP – ∠ABO
= 90° – 40° [∵ ∠OBP = 90°, angles between tangent and radius]
= 50°
![]()
Question 10.
ΔPQR is right angled isosceles triangle, right angled at R. Find value of sin P.
(A) \(\frac{1}{\sqrt{2}}\)
(B) \(\frac{1}{2}\)
(C) 0
(D) 1
Solution:
(A) \(\frac{1}{\sqrt{2}}\)
Explanation:
sin P = \(\frac{1}{\sqrt{2}}\)
Detailed Solution:
∵ ΔPQR is a right angled isosceles triangle i.e.,
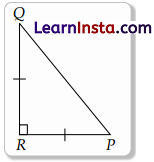
∠R = 90°
∴ PR = RQ
So, ∠P = ∠Q = 45°
Now, sin P = sin 45°
= \(\frac{1}{\sqrt{2}}\)
Question 11.
The value of \(\frac{1}{\tan \theta+\cot \theta}\) =
(A) cos θ sin θ
(B) sec θ sin θ
(C) tan θ cot θ
(D) sec θ cosec θ
Solution:
(A) cos θ sin θ
Explanation:

= cos θ sin θ. [sin2 θ + cos2 θ = 1]
Question 12.
Given that sin θ = \(\frac{a}{b}\) then cos θ is equal to
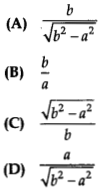
Solution:
(c) \(\frac{\sqrt{b^2-a^2}}{b}\)
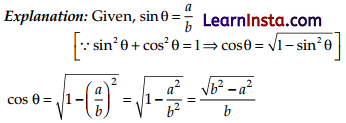
Question 13.
If the perimeter of a circle is half to that of a square, then the ratio of the area of the circle to the area of the square is
(A) 22:7
(B) 11:7
(C) 7:11
(D) 7:22
Solution:
(D) 7:22
Explanation: Let radius of the circle be r cm and side of the square is a cm.
According to the question, perimeter of the circle is half of perimeter of the square.

![]()
Question 14.
Find the area of the sector of a circle of radius 6 cm whose central angle is 30°. (Take x = 3.14)
(A) 7.24 cm2
(B) 8.24 cm2
(C) 9.42 cm2
(D) none of these
Solution:
(C) 9.42 cm2
Explanation:
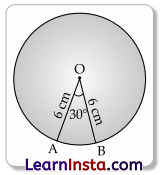
Given, radius of a circle,
OA = OB = 6 cm
(Assuming in figure)
and central angle q = ∠AOB = 30°
By using formula,
area of the sector of a circle
= \(\frac{\theta}{360^{\circ}}\) × πr2
= \(\frac{30^{\circ}}{360^{\circ}}\) × 3.14 × 6 × 6
= 9.42 cm2
Question 15.
The probability expressed as a percentage of a particular occurrence can never be
(A) less than 100
(B) less than 0
(C) greater than 1
(D) anything but a whole number
Solution:
(B) less than 0
Explanation: Probability lies between 0 and 1 and when it is converted into percentage it will be between 0 and 100. So, cannot be negative.
Question 16.
For the following distribution:

the sum of lower limits of median class and modal class is
(A) 15
(B) 25
(C) 30
(D) 35
Solution:
(B) 25
Explanation:
| Class | Frequency | Cumulative frequency |
| 0 – 5 | 10 | 10 |
| 5 – 10 | 15 | 25 |
| 10 – 15 | 12 | 37 |
| 15 – 20 | 20 | 57 |
| 20 – 25 | 9 | 66 |
The modal class is the class having the maximum frequency.
The maximum frequency 20 belongs to class (15 – 20).
Here, ∑fi = n = 66
So, \(\frac{n}{2}\) = \(\frac{66}{2}\) = 33
33 lies in the class 10 – 15.
Therefore, 10 – 15 is the median class.
So, sum of lower limits of (15 – 20) and (10 – 15) is (15 + 10) = 25
Question 17.
Savita has a lamp placed at the center of her square yard, each side measuring 20 m. The light of lamp covers a circle of radius 10 m on yard. What area of the yard is NOT lit by the lamp?
(A) 400π sq.m
(B) 100π sq.m
(C) (40 – 10π) sq.m
(D) (400 – 100π) sq.m
Solution:
(D) (400 – 100π) sq.m
Explanation:
Each side of Savita’s square yard = 20 m
∴ Area of square yard = (side)2
= (20)2 = 400 m2
Radius of circle, where light of lamp covers = 10 m
∴ Area of circle = πr2
= π (10)2 = 100 πm2
Hence, the area of the yard is not lit by the lamp
= Area of square yard – Area of circle
= (400 – 100π) m2
![]()
Question 18.
Which of the following is not a measure of central tendency?
(A) Mean
(B) Median
(C) Mode
(D) range
Solution:
(D) range
Explanation: Range is measure of dispersion.
Directions: In the following questions, A Statement of Assertion (A) is followed by a statement of Reason (R).
Mark the correct choice as.
Question 19.
Assertion (A): If (0, 3), (1, 1) and (-1, 2) are the midpoints of the sides of the triangle, then centroid of the triangle is (0,3).
Reason (R): The centroids of the main triangle and triangle formed by joining the sides of the main triangle is same.
(A) Both (a) and (R) are true and (R) is the correct explanation for (A).
(B) Both (A) and (R) are true but (R) is not the correct explanation for (A).
(C) (A) is true but (R) is false.
(D) (A) is false but (R) is true.
Solution:
(C) (A) is true but (R) is false.
Explanation: In case of assertion;
centroid of triangle =
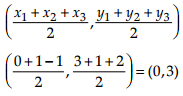
which is a contradiction.
Centroids of the main triangle and triangle formed by joining the sides of the main triangle is same, this is true. Therefore, A is true but R is false.
Question 20.
Assertion (A): For any natural number n, (n)2 is of the form 2q or 2q + 2.
Reason (R): Square of every odd number is odd.
(A) Both (a) and (R) are true and (R) is the correct explanation for (A).
(B) Both (A) and (R) are true but (R) is not the correct explanation for (A).
(C) (A) is true but (R) is false.
(D) (A) is false but (R) is true.
Solution:
(D) (A) is false but (R) is true.
Explanation: Assertion (A): Here, 3 is a natural number whose square is 9 which is odd number while 2q and 2q + 2 are both even numbers. Hence square of every natural can not write in the form of 2q & 2q + 2. Therefore, Assertion is false.
Reason (R): Square of every odd number is odd.
e.g. (3)2 = 9 [3 and 9 both odd].
Therefore, Reason is true.
Section – B(10 Marks)
Question 21.
I am three times as old as my son. Five years later, I shall be two and a half times as old as my son. How old I am and how old is my son?
Solution:
Let my age be x years & my son’s age be y years.
Then, x = 3y …(i)
Five years later, my age = x + 5 years
My Son’s age = y + 5 years
According to the question, x + 5 = \(\frac{5}{2}\)(y + 5)
2x – 5y – 15 = 0
2(3y) – 5y – 15 = 0
y =15
Son’s age = 15 years
My age = 3(y) = 3(15) = 45 years.
Question 22.
Shown below are three triangles. The measures of two adjacent sides and included angle are given for each triangle.
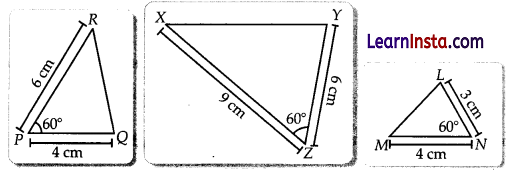
(Note: The figure is not to scale.)
Which of these triangle are similar? Give reason.
Solution:

Taking ∆PQR and ∆XYZ
∠P =∠Z =∠60° …(i)
Also,
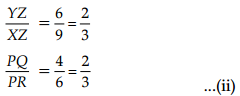
From (i) and (ii),
∆PQR ~ ∆XYZ
![]()
OR
In the figure below, DE || AC and DF || AE. Prove that \(\frac{B F}{F E}=\frac{B E}{E C}\)
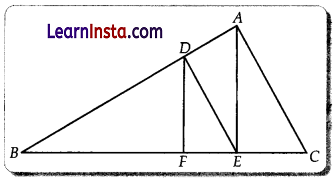
Solution:

Given : DE || AC and DF || AE

Question 23.
In the adjoining figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 30°, find the value of x.
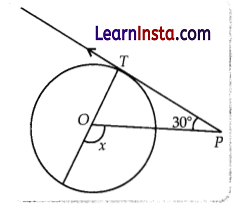
Solution:

PT is a tangent at T to circle
Also, ∠TPO = 30°
So, TPO is right angled triangle with ∠T = 90°
We have, ∠POT = (180°) – (30° + 90°) = 60°
As, x + ∠POT = 180° (linear pair angles)
⇒ x = 180° – 60° = 120°
Question 24.
If sin α = \(\frac{1}{2}\) then find the value of (3 cos α – 4 cos3 α).
Solution:
Given,

![]()
Question 25.
A 3.5 cm chord subtends an angle of 60° at the centre of a circle.
What is the arc length of the minor sector? Draw a rough figure and show your steps.
(Note: Take π as \(\frac{22}{7}\) )
Solution:
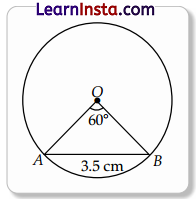
Let AB be the length of chord and ∠O = 60°
∆OAB is an equilateral triangle as AB = BO = OA = 3.5 cm
Length of arc = \(\frac{\theta}{360^{\circ}}\)2πr
= \(\frac{60}{360}\) × 2 × \(\frac{22}{7}\) × \(\frac{35}{10}\)
= 3.66 cm
OR
A semicircle MON is inscribed in another semicircle. Radius OL of the larger semicircle is 6 cm.
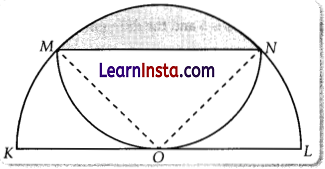
Find the area of the shaded segment in terms of π. Draw a rough figure and show your steps.
Solution:
Draw MO ⊥ ON such that ∆MON is a right angled triangle,
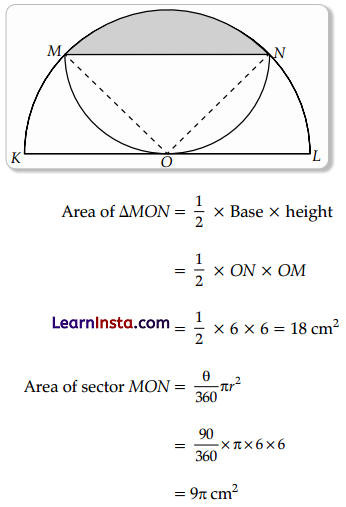
Area of shaded region = Area of sector MON – Area of ∆MON
= 9π – 18 cm2
Section – C(18 Marks)
Question 26.
Prove that √2 + √5 is irrational.
Solution:
Let us assume on the contrary that √2 + √5 is a rational number. Then, there exist co-prime positive integers a and b such that

This contradicts the fact because √2 is irrational.
so, our assumption is wrong.
Hence, √2 + √5 is irrational.
Question 27.
Find the zeroes of the quadratic polynomial 6x2 – 3 – 7x and verify the relationship between zeroes and the coefficients.
Solution:
Given quadratic polynomial p(x) = 6x2 – 7x – 3
For finding zeroes of the polynomial, put p(x) = 0
∴ 6x2 – 7x – 3 = 0
6x2 – 9x + 2x – 3 = 0
3x(2x – 3) + 1 (2x – 3) = 0
(3x + 1) (2x – 3) = 0
x = \(\frac{-1}{3}\), \(\frac{3}{2}\), are the zeroes of the polynomial.
Verification:

![]()
Question 28.
Draw the graphs of the pair of linear equations:
x + 2y = 5 and 2x – 3y = -4
Solution:
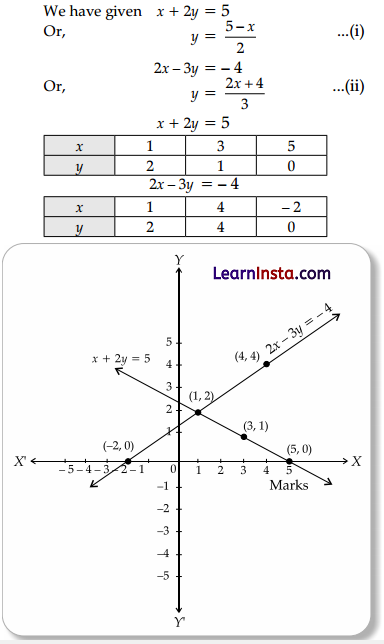
Graph of given pair of linear Equation.
OR
For what value of p will the following system of equations have no solution?
(2p – 1)x + (p – 1)y = 2p + 1; y + 3x – 1 = 0.
Solution:
For (2p – 1)x + (p – 1)y – (2p + 1) = 0
a1 = 2p – 1, b1 = p – 1 and c1 = -(2p + 1)
and for 3x + y – 1 = 0
a2 = 3, b2 = 1 and c2 = -1
The condition for no solution is

⇒ 2p – 1 ≠ 6p + 3
⇒ 4p ≠ -4
⇒ p ≠ -1
∴ Hence, system has no solution when p = 2.
Question 29.
In figure AB is a chord of length 8 cm of a circle of radius 5 cm. The tangents to the circle at A and B intersect at R Find the length of AR.
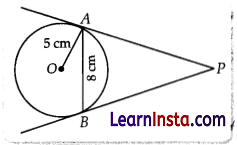
Solution:
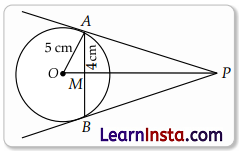
Given, AB = 8 cm
⇒ AM = 4 cm.
∴ OM = \(\sqrt{O A^2-A M^2}\) [By Pythagoras theorem]
OM = \(\sqrt{5^2-4^2}\) = 3 cm.
Let AP = y cm, PM = x cm.
∵ ΔOAP is a right angle triangle.
∴ OP2 = OA2 + AP2 [By Pythagoras theorem]
(x + 3)2 = y2 + 25
⇒ x2 + 9 + 6x = y2 + 25 … (i)
Also, in triangle AMP
x2 + 42 = y2 … (ii)
x2 + 6x + 9 = x2 + 16 + 25
Value of y2 from equation (ii) put in equation (i)
6x = 32

![]()
Question 30.
Prove that: \(\frac{\tan A+\sin A}{\tan A-\sin A}=\frac{\sec A+1}{\sec A-1}\).
Solution:

OR
Prove that: \(\sqrt{\left[\frac{1+\sin A}{1-\sin A}\right]}\) = sec A + tan A.
Solution:

= sec A + tan A.
= R.H.S
Question 31.
Peter throws two different dice together and finds the product of the two numbers obtained. Rina throws a die and squares the number obtained. Who has the better chance to get the number 25.
Solution:
Peter throws two dice together
∴ Total number of possible outcomes = 62 = 36
He get 25 only when he gets (5, 5)
∴ No. of favourable outcomes = 1
P(getting the numbers of product 25) = \(\frac{1}{36}\)
Rina throws one dice
∴ Total number of all possible outcomes = 6
The number where square is 25 is 5
∴ No. of favourable outcomes = 1
P(getting a number whose square is 25) = \(\frac{1}{6}\)
∵ \(\frac{1}{6}\) > \(\frac{1}{36}\)
Hence, Rina has better chances to get the number 25.
Section – D(20 Marks)
Question 32.
Three consecutive natural numbers are such that the square of the middle number exceeds the difference of the squares of the other two by 60. Find the numbers.
Solution:
Let the three consecutive natural numbers be x, x + 1 and x + 2.
Then, according to the given condition
(x + 1)2 = (x + 2)2 – (x)2 + 60
⇒ x2 + 2x + 1 = x2 + 4x + 4 – x2 + 60
⇒ x2 – 2x – 63 = 0
⇒ x2 – 9x + 7x – 63 = 0
⇒ x (x – 9) + 7 (x – 9) = 0
⇒ (x – 9)(x + 7) = 0
Thus, x = 9 or x = – 7
Rejecting -7, we get x = 9
Hence, three numbers are 9, 10 and 11.
OR
(a) The difference of two natural numbers is 5 and the difference of their reciprocals is \(\frac{1}{10}\). Find the numbers.
(b) What is the general form of the quadratic equation?
Solution:
Given, difference of two natural numbers is 5.
Let the x, (x + 5) are two natural numbers

⇒ x2 + 5x – 50 = 0
By splitting the middle term, we get
⇒ x2 + 10x – 5x – 50 = 0
⇒x(x + 10) – 5(x + 10) = 0
⇒ (x + 10)(x – 5) = 0
⇒ x = 5 and x = -10
But given two numbers are natural numbers.
Therefore, x = 5
Here, the required natural numbers are x = 5 and
x + 5 = 5 + 5 = 10
(b) ax2 + bx + c = 0
![]()
Question 33.
(a) Prove that a line drawn parallel to one side of a triangle to intersect the other two sides in distinct points, divides the two sides in the same ratio.
Solution:
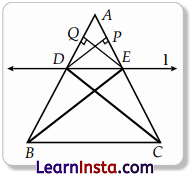
Given: In DABC, line l is parallel to side BC and intersects other two sides at the point D and E respectively.

OR
(b) In the given figure, \(\frac{Q R}{Q S}=\frac{Q T}{P R}\) and ∠1 = ∠2. Prove that ΔPQS ~ ΔTQR
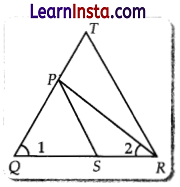
Solution:
Given: \(\frac{Q R}{Q S}=\frac{Q T}{P R}\)
∠1 = ∠2
To Prove: ΔPQS ~ ΔTQR
Proof: ∠1 = ∠2 (Given)
∴ PQ = PR …(1) [Opposite sides of equal angles in DPOR]
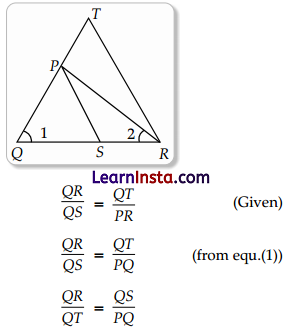
and ∠1 is common
∴ ΔPQS ~ ΔTQR (SAS Test)
Hence Proved.
Question 34.
The boilers are used in thermal power plants to store water and then used to produce steam. One such boiler consists of a cylindrical part in middle and two hemispherical parts at its both ends.
Length of the cylindrical part is 7 m and radius of cylindrical part is \(\frac{7}{2}\)m.
Find the total surface area and the volume of the boiler. Also, find the ratio of the volume of cylindrical part to the volume of one hemispherical part.
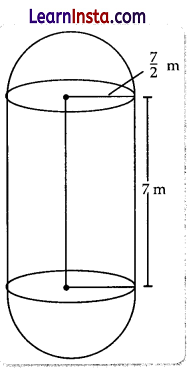
Solution:
Length of cylindrical part = 7 m

![]()
OR
An ice-cream filled cone having radius 5 cm and height 10 cm is as shown in the figure. Find the volume of the ice-cream in 7 such cones.
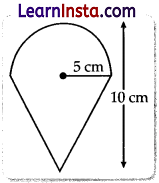
Solution:

Given,
Radius of cone (r) = Radius of hemisphere (r) = 5 cm
Height of Ice-Cream (H) = 10 cm
Height of Cone (h) = Height of Ice-Cream – Height of hemisphere
= 10 – 5
= 5 cm
No. of Cones = 7
Volume of ice cream in one cone = Vol. of cone + Vol. of hemisphere

= 392.85 cm3
Volume of ice cream in 7 cones
= 392.85 × 7 cm3
= 2750 cm3
= 2.75 litres
Question 35.
Daily wages of 110 workers, obtained in a survey, are tabulated below:

Compute the mean daily wages and modal daily wages of these workers.
Solution:

Section – E(12 Marks)
Question 36.
Your elder brother wants to buy a car and plans to take loan from a bank for his car. He repays his total loan of ₹1,18,000 by paying every month starting with the first instalment of ₹1000. If he increases the instalment by ₹100 every month, answer the following:

(i) Find the amount paid by him in the 30th instalment.
(ii) Find the amount paid by him in the 30 instalments.
(iii) If total instalments are 40 then find the amount paid in last instalment?
Solution:
(i) According to given situation,
1000, 1100, 1200, 1300, ……. Is the given A.P
30th instalment = a30
an = a + (n – 1)d
a30 = 1000 + (30 – 1)(100)
= 1000 + 2900
= 3900
(ii) Sum of amounts in 30 instalments = S30
Sn = \(\frac{n}{2}\) [a + a30]
S30 = \(\frac{30}{2}\) [1000 + 3900]
= 15 × 4900 = 73,500
(iii)If number of instalments = 40. i.e., n = 40
an = a + (n – 1)d
a40 = 1000 + (40 – 1)100
= 1000 + 3900
= 4900
![]()
OR
Find the ratio of 1st instalment to the last instalment.
Solution:
Amount in first instalment = 1000
Amount in last instalment = amount in 40th
instalment = 4900
Ratio = 1000 : 4900 = 10 : 49
Question 37.
The class X students school in Krishnagar have been alloted a rectangular plot of land for their gardening activity. Saplings of Gulmohar are planted on the boundary at a distance of 1 m from each other. There is triangular grassy lawn in the plot as shown in the figure. The students are to sow seeds of flowering plants on the remaining area of the plot.
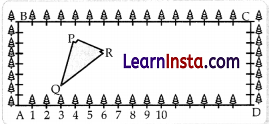
(i) Taking A as origin, find the coordinates of P.
(ii) Taking C as origin find the coordinates of R.
(iii) Taking A as origin, find the length of PQ.
OR
If C is the origin find midpoint of QR.
Solution:
(i) If A is the origin, AD is x-axis and AB represents y-axis.
Then Coordinates of vertices P are (4, 6).
(ii) If C is the origin then BC is x-axis and CD represents y-axis. Then the coordinates of R are (–10, –3).
(iii) If A is the origin, coordinates of P and Q are (4, 6) and (3, 2) respectively.

Question 38.
A group of students of class X visited India Gate on an education trip. The teacher and students had interest in history as well. The teacher narrated that India Gate, official name Delhi Memorial, originally called All-India War Memorial, monumental sandstone arch in New Delhi, dedicated to the troops of British India who died in wars fought between 1914 and 1919. The teacher also said that India Gate, which is located at the eastern end of the Rajpath (formerly called the Kings way), is about 138 feet (42 metres) in height.

(i) What is the angle of elevation if they are standing at a distance of 42 m away from the monument?
Solution:
Height of India gate = 42 m
Distance between students and India Gate = 42 m
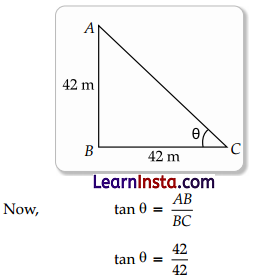
tan θ = 1
tan θ = tan 45°
θ = 45°
Hence, angle of elevation = 45°
(ii) They want to see the tower at an angle of 60°. So, they want to know the distance where they should stand and hence find the distance.
Solution:
Height of India Gate = 42 m
Angle of elevation = 60°
Let the distance between students and India gate = x m.
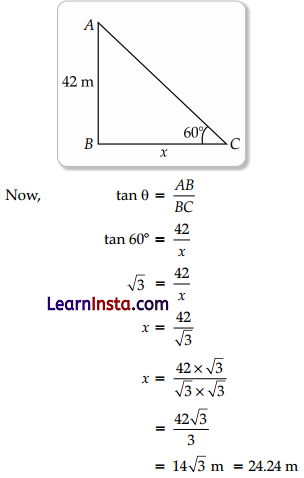
![]()
(iii) If the altitude of the Sun is at 60°, then find the height of the vertical tower that will cast a shadow of length 20 m.
Solution:
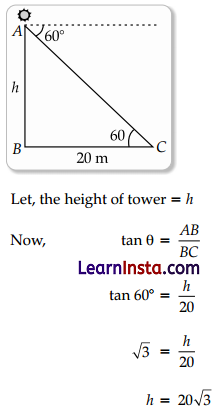
OR
The ratio of the length of a tower and its shadow is 1:1. The find angle of elevation of the Sun.
Solution:
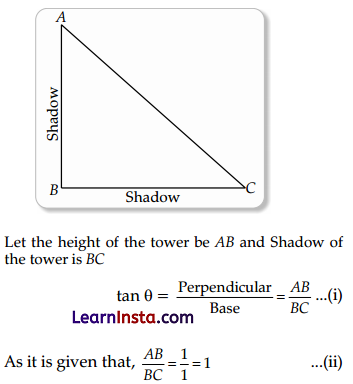
Therefore, From (i) and (ii), we get
θ = 45° as tan 45° = 1
Must Read:
INDHOTEL Pivot Point Calculator