Free access of the complete Ganita Prakash Book Class 6 Solutions and Chapter 10 The Other Side of Zero Class 6 NCERT Solutions Question Answer are crafted in simple format to align with the latest CBSE syllabus.
Class 6 Maths Chapter 10 The Other Side of Zero Solutions
The Other Side of Zero Class 6 Solutions Questions and Answers
10.1 Bela’s Building of Fun Figure it Out (Page No. 245)
Question 1.
You start from Floor +2 and press -3 in the lift. Where will you reach? Write an expression for this movement.
Solution:
2 + (-3) = -1
Question 2.
Evaluate these expressions (you may think of them as Starting Floor + Movement by referring to the Building of Fun).
(a) (+1) + (+4) = _______________
Solution:
Here, the starting floor is +1 (Food Court) and the number of button presses is +4.
Therefore, Target floor = Starting floor + Movement
= (+1) + (+4)
= +5 (Sports centre).
(b) (+4) + (+1) = _______________
Solution:
Here, the starting floor is +4 (Ice-cream centre) and the number of button presses is +1 (Food court).
Therefore, Target floor = Starting floor + Movement
= (+4) + (+1)
= +5 (Sports centre).
(c) (+4) + (-3) = _______________
Solution:
Here, the starting floor is +4 (Ice-cream centre) and the number of button presses is (-3).
Therefore, Target floor = Starting floor + Movement
= (+4) + (-3)
= +1 (Food court).
(d) (-1) + (+2) = _______________
Solution:
Here, the starting floor is (-1) (Toys centre) and the number of button presses is +2.
Therefore, Target floor = Starting floor + Movement
= (-1) + 2
= +1 (Food court).
(e) (-1) + (+1) = _______________
Solution:
Here, the starting floor is -1 (Toys centre) and the number of button presses is +1.
Therefore, Target floor = Starting floor + Movement
= (-1) + (+1)
= 0 (Welcome Hall means Ground floor).
(f) 0 + (+2) = _______________
Solution:
Here, the starting floor is 0 (Ground floor) and the number of button presses is +2.
Therefore, Target floor = Starting floor + Movement
= (0) + (+2)
= +2 (Art centre)
(g) 0 + (-2) = _______________
Solution:
Here, the starting floor is 0 (Ground floor) and the number of button presses is -2.
Therefore, Target floor = Starting floor + Movement
= 0 + (-2)
= -2 (Video games).
![]()
Question 3.
Starting from different floors, find the movements required to reach floor – 5.
e.g. if I start at floor + 2,1 must press – 7 to reach floor – 5. The expression is (+ 2) + (- 7) = – 5.
Find more such starting positions and the movements needed to reach floor – 5 and write the expressions.
Solution:
Starting at Floor + 3
Movement needed – 8
Expression (+3) + (- 8) = – 5
Starting at Floor 0
Movement needed – 5
Expression (0) + (- 5) = – 5
Starting at Floor – 2
Movement needed – 3
Expression (- 2) + (- 3) = – 5
Starting at Floor – 1
Movement needed – 4
Expression (- 1) + (- 4) = – 5
Starting at Floor + 7
Movement needed – 12
Expression (+ 7) + (- 12) = – 5
Starting at Floor – 3
Movement needed – 2
Expression (- 3) + (- 2) = – 5
Starting at Floor +10
Movement needed -15
Expression (+ 10) + (- 15) = – 5
InText Questions
Question 1.
What do you press to go four floors up? What do you press to go three floors down? (Page 243)
Solution:
We press +4 (+ + + + ) to go four floors up and we press -3 (- – -) to go three floors down.
Question 2.
Number all the floors in the Building of Fun. (Page 244)
Solution:
Space is on Floor +6
Sports is on Floor +5
Ice Cream is on Floor +4
Books is on Floor +3
Art Centre is on Floor +2
Food court is on Floor +1
Welcome Hall is on Floor +0
Toys Shop is on Floor -1
Video Games is on Floor -2
Cinema is on Floor -3
Ghost House is on Floor -4
Dinosaur is on Floor -5
10.1 Bela’s Building of Fun Figure it Out (Page No. 246)
Question 1.
Evaluate these expressions by thinking of them as the resulting movement of combining button presses:
(a) (+1) + (+4) = __________
(b) (+ 4) + (+ 1) = __________
(c) (+ 4) + (- 3) + (- 2) = __________
(d) (-1) + (+2) + (-3) = __________
Solution:
(a) (+ 1) + (+4) = +5
(b) (+ 4) + (+ 1) = +5
(c) (+ 4) + (- 3) + (- 2) = {(+ 4) + (- 3)} + (- 2)
= (+1) + (- 2) = -1
(d) (-1) + (+2) + (-3) = {(-1) + (+2)} + (-3)
= (+1) + (-3) = -2
InText Questions
Back to Zero!
Question 1.
Write the inverses of these numbers: (Page 246)
+4, -4, -3, 0, +2, -1.
Solution:
The inverse of+4 is -4, the inverse of-4 is +4, the inverse of-3 is +3, the inverse of 0 is 0, the inverse of +2 is -2, and the inverse of-1 is +1. it Connect the inverses by drawing lines.
Question 2.
Connect the inverses by drawing lines.
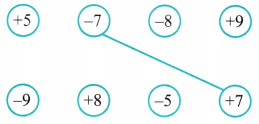
Solution:
The inverses are connected with their respective numbers by the lines as shown below.

Question 3.
Comparing numbers using floors
Question 4.
Who is on the lowest floor?
1. Jay is in the Art Centre. So, he is on Floor +2.
2. Asin is in the Sports Centre. So, she is on Floor __________.
3. Binnu is in the Cinema Centre. So, she is on Floor __________
4. Aman is in the Toys Shop. So, he is on Floor __________.
Solution:
1. Jay is in the Art Centre. So, he is on Floor +2.
2. Asin is in the Sports Centre. So, she is on Floor +5.
3. Binnu is in the Cinema Centre. So, she is on Floor-3.
4. Aman is in the Toys Shop. So, he is on Floor -1.
Among the four children, Binnu on the lowest floor.
10.1 Bela’s Building of Fun Figure it Out (Page No. 247)
Question 1.
Compare the following numbers using the Building of Fun and fill in the boxes with < or >.
(a) -2 ![]() +5
+5
(b) -5 ![]() +4
+4
(c) -5 ![]() -3
-3
(d) +6 ![]() -6
-6
(e) 0 ![]() -4
-4
(f) 0 ![]() +4
+4
Solution:
The number on the upper side of the number line is greater than the number on the lower side of the number line.
(a) -2 < 5
(b) -5 < 4
(c) -5 < -3
(d) +6 > -6
(e) 0 > -4
(f) 0 < +4
![]()
Question 2.
Imagine the Building of Fun with more floors. Compare the numbers and fill in the boxes with < or >:
(a) -10 ![]() -12
-12
(b) +17 ![]() -10
-10
(c) 0 ![]() -20
-20
(d) +9 ![]() -9
-9
(e) -25 ![]() -7
-7
(f) +15 ![]() -17
-17
Solution:
(a) -10 > -12
(b) +17 > -10
(c) 0 > -20
(d) +9 > -9
(e) -25 < -7
(f) +15 > -17
Question 3.
If Floor A = -12, Floor D = -1, and Floor E = +1 in the building shown on the right as a line, find the numbers of Floors B, C, F, G, and H.

Solution:
Let’s mark the numbers on the line.
0, -1, -2, -3,…………, -12 and 1, 2, 3,……….., 12
Now count each floor, and we get the number of floors.
Here, B = -9, C = -6, F = +2, G = +6 and H = +11
Question 4.
Mark the following floors of the building shown on the right.
(a) -7
(b) -4
(c) +3
(d) -10
Solution:
Here, one line is considered as one floor.
The floor above floor 0 is marked with positive numbers and the floor below 0 is numbered with negative numbers.
Now let’s mark the following numbers (-7, -4, +3, -10) in the building by circling the floor.

InText Questions
Question 1.
Evaluate 15-5, 100 – 10 and 74 – 34 from this perspective. (Page 248)
Solution:
15-5 means 5 taken away from 15 is 10.
∴ 15 – 5 = 10
100 – 10 means 10 taken away from 100 is 90.
∴ 100 – 10 = 90
74 – 34 means 34 taken away from 74 is 40.
∴ 74 – 34 = 40
10.1 Bela’s Building of Fun Figure it Out (Page No. 249)
Question 1.
Complete these expressions. You may think of them as finding the movement needed to reach the target floor from the starting floor.
(a) (+1) – (+4) = ________________
(b) (0) – (+2) = ________________
(c) (+4) – (+1) = ________________
(d) (0) – (-2) = ________________
(e) (+4)-(-3) = ________________
(f) (-4) – (-3) = ________________
(g) (-1) – (+2) = ________________
(h) (-2) – (-2) = ________________
(i) (-1) – (+1) = ________________
(j) (+3)-(-3) = ________________
Solution:
(a) (+ 1) -(+4) = -3
Starting at Floor + 1, moving down 4 floors lands you at Floor-3.
(b) (0) – (+ 2) = — 2
Starting at Floor 0, moving down 2 floors lands you at Floor – 2.
(c) (+4) – (+ 1) = + 3
Starting at Floor + 4, moving down 1 floor lands you at Floor + 3.
(d) (0) — (-2) = + 2
Starting at Floor 0, moving up 2 floors (since, subtracting a negative is like adding a positive) lands you at Floor + 2.
(e) (+ 4) — (— 3) = + 7
Starting at Floor + 4, moving up 3 floors (subtracting a negative) lands you at Floor + 7.
(f) (— 4) – (—3) = — 1
Starting at Floor – 4, moving up 3 floors (subtracting a negative) lands you at Floor – 1.
(g) (-1) – (+ 2)=- 3
Starting at Floor – 1, moving down 2 floors lands you at Floor-3.
(h) (- 2) – (- 2) = 0
Starting at Floor – 2, moving up 2 floors (subtracting a negative) lands you at Floor 0.
(i) (- 1) – (+1) = -2
Starting at Floor – 1, moving down 1 floor lands you at Floor – 2.
(j) (+3) – (-3) = + 6
Starting at Floor + 3, moving up 3 floors (subtracting a negative) lands you at Floor + 6.
![]()
10.1 Bela’s Building of Fun Figure it Out (Page No. 251)
Complete these expressions.
(a) (+40) + ____ = +200
(b) (+40) + ____ = -200
(c) (-50) +____ = +200
(d) (-50) + ____ = -200
(e) (-200) – (-40) = ____
(f) (+200) – (+40) = ____
(g) (-200) -(+40) = ____
Check your answers by thinking about the movement in the mineshaft.
Solution:
(a) (+200) – (+40) = +160.
Therefore, (+40) + (+160) = +200
(b) (-200) – (+40) = -240.
Therefore, (+40) + (-240) = -200
(c) (+200) – (-50) = +250.
Therefore, (-50) + (+250) = +200
(d) (-200) – (-50) = -150.
Therefore, (-50) + (-150) = -200
(e) (-200) -(-40) = -160
(f) (+200) – (+40) = +160
(g) (-200) – (+40) = -240
InText Questions
Question 1.
Try evaluating the following expressions by similarly drawing or imagining a suitable lift: (Page 251)
(a) -125 + (-30)
(b) +105 – (-55)
(c) +105 + (+55)
(d) +80 – (-150)
(e) +80 + (+150)
(f) -99 – (-200)
(g) -99 + (+200)
(h) + 1500 – (-1500)
Solution:
(a) -125 + (-30) = -155
(b) +105 – (-55) = +160
(c)+105 + (+55) = +160
(d) +80-(-150) = +230
(e) +80+ (+150) = +230
(f) -99-(-200) = +101
(g)-99+ (+200) = +101
(h) +1500- (-1500) = +3000
10.1 Bela’s Building of Fun Figure it Out (Page No. 253 – 254)
![]()
Question 1.

Mark 3 positive numbers and 3 negative numbers on the number line above.
Solution:

Question 2.
Write down the above 3 marked negative numbers in the following boxes:
![]()
Solution:
-3, -6, -9
Question 3.
Is 2 > -3? Why? Is -2 < 3? Why? Solution: Is 2 > -3?
Yes, 2 is a positive number and -3 is a negative number. We know that positive numbers are always greater than negative numbers.
Hence, 2 is greater than -3.
Is -2 < 3? Why?
∴ Yes, -2 is less than 3 because -2 is a negative number and 3 is a positive number.
Hence -2 < 3.
4. What are
(i) -5 + 0
(ii) 7 + (-7)
(iii) -10 + 20
(iv) 10 – 20
(v) 7 – (-7)
(vi) -8 – (-10)?
Solution:
(i) -5 + 0
Adding 0 to any number does not change the value of the number.
-5 + 0 = -5
(ii) 7 + (-7)
Adding a number to its negative counterpart results in 0.
7 + (-7) = 0
(iii) -10 + 20
To add numbers with different signs, subtract the smaller absolute value from the larger absolute value and take the sign from the larger absolute value.
-10 + 20 = 10
(iv) 10 – 20
Subtracting a larger number from a smaller number gives a negative result.
10 – 20 = -10
(v) 7 – (-7)
Subtracting a negative number is the same as adding the positive counterpart of the number.
7 – (-7) = 7 + 7 = 14
(vi) -8 – (-10)
Subtracting a negative number is the same as adding the positive counterpart of the number.
-8 – (-10) = -8 + 10 = 2
![]()
InText Questions
Question 1.
Use unmarked number lines to evaluate these expressions: (Page 255)
(a) -125 + (-30) = _______________
(b) +105 -(-55) = _______________
(c) +80 – (-150) = _______________
(d) -99 – (-200) = _______________
Solution:
(a) -125 + (-30) = -155
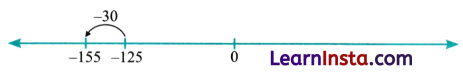
(b) Subtracting a negative number is the same as adding the corresponding positive number.
So, +105 – (-55) means +105 + (+55) = 160. That is,
+105 – (-55) = +160

Similarly,
(c) +80 – (-150) = +230

(d) -99 – (-200) = +101

10.2 The Token Model Figure it Out (Page No. 257)
Question 1.
Complete the additions using tokens.
(a) (+6) + (+4)
Solution:

∴ (+6) + (+4) = +10
(b) (-3) + (-2)
Solution:

∴ (-3) + (-2) = -5
(c) (+5) + (-7)
Solution:

∴ (+5) + (-7) = -2
(d) (-2) + (+6)
Solution:
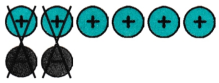
∴ (-2) + (+6) = +4
Question 2.
Cancel the zero pairs in the following two sets of tokens. On what floor is the lift attendant in each case? What is the corresponding addition statement in each case?
Solution:

The lift attendant is on the floor -2.
The corresponding addition statement is (+3) + (-5) = -2.
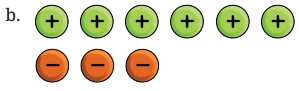
Solution:

The lift attendant is on the floor +3.
The corresponding addition statement is (+6) + (-3) = +3.
10.2 The Token Model Figure it Out (Page No. 258)
Question 1.
Evaluate the following differences using tokens. Check that you get the same result as with other methods you now know:
(a) (+10) – (+7)
Solution:
Here, from 10 positives take away 7 positives.
![]()
Hence, (+10) – (+7) = +3
(b) (-8) – (-4)
Solution:
Here, from -8 negatives take away -4 negatives

Hence, (-8) – (-4) = -4
(c) (-9) – (-4)
Solution:
Here, from -9 negatives take away -4 negatives.
![]()
Hence, (-9) – (-4) = -5
(d) (+9) – (+12)
Solution:
There are not enough tokens to take out 12 positives from 9 positives.
So, we put an extra 3 zero pairs (1 pair = a positive and a negative).
Now we can take out 12 positives.

Hence, (+9) – (+12) = -3
(e) (-5) – (-7)
Solution:
There are not enough tokens to take out -7 negatives from -5 negatives.
So, we put an extra two zero pairs (1 pair = a positive and a negative).
Now we can take out -7 negatives.
![]()
Hence, (-5) – (-7) = +2
(f) (-2) – (-6)
Solution:
There are not enough tokens to take out -6 negatives from -2 negatives.
So, we put an extra four zero pairs (1 pair = a positive and a negative).
Now we can take out -6 negatives.
![]()
Hence, (-2) – (-6) = +4
Question 2.
Complete the subtractions:
(a) (-5) – (-7)
Solution:
There are not enough tokens to take out -7 negatives from -5 negatives.
So, we put an extra two zero pairs (1 pair = a positive and a negative).
Now we can take out -7 negatives.
![]()
Hence, (-5) – (-7) = +2
![]()
(b) (+10) – (+13)
Solution:
There are not enough tokens to take out 13 positives from 10 positives.
So, we put an extra 3 zero pairs (1 pair = a positive and a negative).
Now we can take out 13 positives.

Hence, (+10) – (+13) = -3
(c) (-7) – (-9)
Solution:
There are not enough tokens to take out -9 negatives from -7 negatives.
So, we put an extra two zero pairs (1 pair = a positive and a negative).
Now we can take out -9 negatives.

Hence, (-7) – (-9) = +2
(d) (+3) – (+8)
Solution:
There are not enough tokens to take out 8 positives from 3 positives.
So, we put an extra 5 zero pairs (1 pair = a positive and a negative).
Now we can take out 8 positives.

Hence, (+3) – (+8) = -5
(e) (-2) – (-7)
Solution:
There are not enough tokens to take out -7 negatives from -2 negatives.
So, we put an extra two zero pairs (1 pair = a positive and a negative).
Now we can take out -7 negatives.

Hence, (-2) – (-7) = +5
(f) (+3) – (+15)
Solution:
There are not enough tokens to take out 15 positives from 3 positives.
So, we put an extra 12 zero pairs (1 pair = a positive and a negative).
Now we can take out 15 positives.

Hence, (+3) – (+15) = -12
![]()
Question 2.
2. Complete the subtractions:
(a)
(-5) – (-7)
(b) (+10) – (+13)
(c) (-7) – (-9)
(d) (+3) – (+8)
(e) (-2) – (-7)
(f) (+3) – (+15)
Solution:
(a) (-5) – (-7) = +2
(b) (+10) – (+13) =-3
(c) (-7) – (-9) = +2
(d) (+3) – (+8) = -5
(e) (-2) – (-7) = +5
(f) (+3) – (+15) = -12
10.2 The Token Model Figure it Out (Page No. 259)
Question 1.
Try to subtract: -3 – (+5).
How many zero pairs will you have to put in? What is the result?
Solution:
-3 – (+5) = -3 – 5 = -8
We have to put on 5 zero pairs.
The answer is -8.
Question 2.
Evaluate the following using tokens.
(a) (-3)-(+10)
(b) (+ 8) – (- 7)
(c) (- 5) – (+ 9)
(d) (-9)- (+10)
(e)(+6)-(-4)
(f) (- 2) – (+ 7)
Solution:
(a) You need to subtract +10 (remove 10 positive tokens), but you do not have any positive tokens available. Adding 10 zero pairs gives you 10 positive tokens and 10 negative tokens. Now, remove the + 10 (positive tokens).You are left with the original – 3 tokens plus the additional – 10 tokens from the zero pairs.
(-3)- (+10) = -13
(result of the other problems can be solved in the same way)
Do yourself
![]()
10.3 Integers in Other Places Figure it Out (Page No. 260)
Question 1.
Suppose you start with 0 rupees in your bank account, and then you have crediip of ₹ 30, ₹ 40, and ₹ 50, and debits of ₹ 40, ₹ 50, and ₹ 60. What is your bank account balance now?
Solution:
Consider ‘credits’ as positive numbers and ‘debits’ as negative numbers.
Total credits = (+30) + (+40) + (+50) = +120
Total debits = (-10) + (-50) + (-60) = -150
Account balance = Total credits + Total debits = (+120)+ (-150) = -30
Hence, the account balance is -₹30.
Question 2.
Suppose you start with 0 rupees in your bank account, and then you have debits of ₹ 1, 2, 4, 8, 16, 32, 64, and 128, and then a single credit of ₹ 256. What is your bank account balance now?
Solution:
Here, Debits = ₹ 1 + ₹ 2 + ₹ 4 + ₹ 8 + ₹ 16 + ₹ 32 + ₹ 64 + ₹ 128 = ₹ 255
∴ Balance = Credits – Debits
= ₹ 256 – ₹ 255
= ₹ 1
Therefore, your bank account balance is ₹ 1.
Question 3.
Why is it generally better to try and maintain a positive balance in your bank account? What are circumstances under which it may be worthwhile to temporarily have a negative balance?
Solution:
In case of a negative balance, can affect your credit score. If you spend more money than have in your account, your bank may or may not cover your transactions. Negative balance can lead to overdraft fees, account closure, etc.
10.3 Integers in Other Places Figure it Out (Page No. 261)
Question 1.
Looking at the geographical cross section fill in the respective heights.

Solution:
A = + 1500 m
B = – 500 m
C = + 300 m
D = – 1200 m
Question 2.
Suppose you start with 0 rupees in your bank account, and then you have debits of ₹ 1, 2, 4, 8, 16, 32, 64, and 128, and then a single credit of ₹ 256. What is your bank account balance now?
Solution:
Here, Debits = ₹ 1 + ₹ 2 + ₹ 4 + ₹ 8 + ₹ 16 + ₹ 32 + ₹ 64 + ₹ 128 = ₹ 255
∴ Balance = Credits – Debits
= ₹ 256 – ₹ 255
= ₹ 1
Therefore, your bank account balance is ₹ 1.
Question 3.
Can you write the points A, B, …, G in a sequence of decreasing order of heights? Can you write the points in a sequence of increasing order of heights?
Solution:
The sequence of decreasing order of heights: A, E, C, G, F, B, and D.
The sequence of increasing order of heights: D, B, F, G, C, E, and A.
Question 4.
What is the highest point above sea level on Earth? What is its height?
Solution:
The highest point on Earth is Mount Everest at a height of 8848 m above sea level.
Question 5.
What is the lowest point of sea level on land or the ocean floor? What is its height? (This height should be negative).
Solution:
The lowest known point on the Earth is Marina Trench, in the Pacific Ocean, at a depth of 11034 m below sea level.
10.3 Integers in Other Places Figure it Out (Page No. 262)
Question 1.
Do you know that there are some places in India where temperatures can go below 0°C? Find out the places in India where temperatures sometimes go below 0°C. What is common among these places? Why does it become colder there and not in other places?

Solution:
Places in India where temperatures can go below 0°C are:
- Sela Pass, Tawang
- Siachen Glacier
- Lachen and Thangu
- Leh and Ladakh
- Spiti Valley
- Sonamarg
- Rohtang Pass
The common thing about these places are they are situated at a higher altitude than sea level. As air rises, air pressure drops and the gas expands. To expand, the gas needs energy which it takes from the surrounding atmosphere. This cools off the surrounding air. Hence, it becomes cool at higher altitudes.
Question 2.
Leh in Ladakh gets very cold during winter. The following is a table of temperature readings taken during different times of the day/night in Leh on a day in November. Match the temperature with the appropriate time of the day/night.

Solution:

10.4 Explorations with Integers Figure it Out (Page No. 263 – 264)
Question 1.
Do the calculations for the second grid above and find the border sum.

Solution:
Top row = 5 + (- 3) + (- 5) = – 3
Bottom row = (- 8) + (- 2) + 7 = – 3
Left column = 5+ 0 + (-8) = -3
Right column = (- 5) + (- 5) + 7 = – 3
The board sum of the second grid is – 3.
Question 2.
Complete the grids to make the required border sum

Solution:

Question 3.
For the last grid above, find more than one way of filling the numbers to get border sum -4.
Solution:
We can fill up the above grids in so many ways.
Following are few ways to fill the last grid.
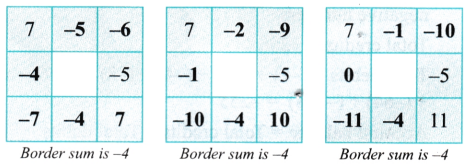
Question 4.
Which other grids can be filled in multiple ways? What could be the reason?
Solution:
Grid with a larger size (more rows and columns) is likely to have multiple solutions. This is because there are more degrees of freedom to distribute numbers while maintaining the border sum.
Question 5.
Make a border integer square puzzle and challenge your classmates.
Solution:
Do it yourself.
10.4 Explorations with Integers Figure it Out-1 (Page No. 265)
Question 1.
Try afresh, choose different numbers this time. What sum did you get? Was it different from the first time? Try a few more times!
Solution:
Let’s circle the number -5.
Now as per the game, let’s strike out the row and column with the number -5.
Now try yourself.
Question 2.
Play the same game with the grids below. What answer did you get?

Solution:
(a) Let’s circle the number 1.
Now as per the game, let’s strike out the row and column with number 1.

Again let’s circle the number 13.
Let’s strike out the row and column with the number 13.

Again let’s circle the number -20.
Let’s strike out the row and column with the number -20.

Again let’s circle the balance number 2.
Let’s strike out the row and column with number 2.

Now let’s add the circled numbers = 1 + 13 – 20 – 2= 14 – 22 = -8 which is the required answer.
(b) Let’s circle the number 0.
Now as per the game, let’s strike out the row and column with the number 0.

Again let’s circle the number -5.
Let’s strike out the row and column with the number -5.

Again let’s circle the number 1.
Let’s strike out the row and column with the number 1.

Let’s strike out the row and column with the number -10.
Again let’s circle the balance number -10.

Now let’s add the circled numbers = 0 + (-5) + 1 + (-10) = -14 which is the required answer.
Question 3.
What could be so special about these grids? Is the magic in the numbers or the way they are arranged or both? Can you make more such grids?
Solution:
In these grids the numbers are arranged in a definite pattern.
The magic lies in the way the numbers are arranged in the grid. They follow a definite pattern.
One such grid is:

Numbers: The numbers in a grid can follow specific patterns or sequences, such as magic squares where the sums of numbers in each row, column, and diagonal are the same.
Arrangement: The way elements are arranged in a grid can create visual balance and harmony.
10.4 Explorations with Integers Figure it Out-2 (Page No. 265 – 266)
Question 1.
Write all the integers between the given pairs, in increasing order.
(3) 0 and -7
(b) -4 and 4
(c) -8 and -15
(d) -30 and -23
Solution:
(a) The integers between 0 and -7 in increasing order are: -6, -5, -4, -3, -2, and -1.
(b) The integers between -4 and 4 in increasing order are: -3, -2, -1, 0, 1, 2, and 3.
(c) The integers between -8 and -15 in increasing order are: -14, -13, -12, -11, -10, and -9.
(d) The integers between -30 and -23 in increasing order are: -29, -28, -27, -26, -25, and -24.
Question 2.
Give three numbers such that their sum is -8.
Solution:
2 + 6 + (-16) = -8
Question 3.
There are two dice whose faces have these numbers: -1, 2, -3, 4, -5, 6. Tlje smallest possible sum upon rolling these dice is -10 = (-5) + (-5) and the largest possible sum is 12 = (6) + (6). Some numbers between (-10) and (+12) are not possible to get by adding numbers on these two dice. Find those numbers.
Solution:
All possible combinations of numbers on both dice will be: (-5, -5), (-5, -3), (-5, -1), (-5, 2), (-5, 4), (-5,6), (-3, -5), (-3, -3), (-3, -1), (-3,2), (-3,4), (-3,6), (-1, -5), (-1, -3), (-1, -1), (-1, 2), (-1, 4), (-1, 6), (2, -5), (2, -3), (2, -1), (2, 2), (2, 4), (2, 6), (4, -5), (4, -3), (4, -1), (4, 2), (4, 4), (4, 6), (6, -5), (6, -3), (6,-1), (6, 2), (6, 4), (6, 6).
Unique sums are: -10, -8, -6, -4, -3, -2, -1, 1, 3, 4, 5, 6, 8, 10, 12
So, the numbers between -10 and 12 that are not possible as a sum of the numbers on the dice are -9, -7, -5, 0, 2, 7, 9, and 11.
![]()
Question 4.
Solve these:

Solution:
(a) 8 – 13 = -5
(b) -8 – (13) = -8 – 13 = -21
(c) -13 – (-8) = -13 + 8 = -5
(d) (-13) + (-8) = -13 – 8 = -21
(e) 8 + (-13) = 8 – 13 = -5
(f) -8 – (-13) = -8 + 13 = 5
(g) (13) – 8 = 13 – 8 = 5
(h) 13 – (-8) = 13 + 8 = 21
Question 5.
Find the years below.
(a) From the present year, which year was it 150 years ago? ____________
(b) From the present year, which year was it 2200 years ago? ____________
(Hint: Recall that there was no year 0.)
(c) What will be the year 320 years after 680 BCE? ____________
Solution:
(a) 2024 – 150 = 1874
(b) 2024 – 2200 = -176 = 176 BCE
(c) -680 + 320 = -360 = 360 BCE
Question 6.
Complete the following sequences.
(a) (- 40), (- 34), (- 28), (- 22), ____, ____, ____
(b) 3, 4, 2, 5, 1, 6, 0, 7, ____, ____, ____
(c) ____, ____ 12, 6, 1, (-3), (-6), ____, ____, ____
Solution:
(a) (40), (- 34), (- 28), (- 22), (- 16), (- 10), (- 4)
(b) 3, 4, 2, 5, 1, 6, 0, 7, -1, 8, -2
(c) 27, 19, 12, 6, 1, (- 3), (- 6), (- 8), (- 9), (- 9)
Question 7.
Flere are six integer cards: (+1), (+7), (+18), (-5), (-2), (-9).
You can pick any of these and make an expression using addition(s) and subtraction(s).
Here is an expression: (+18) + (+1) – (+7) – (-2) which gives a value (+14).
Now, pick cards and make an expression such that its value is closer to (-30).
Solution:
(-9) – (+18) + (-2) = -29, which is closer to -30 Answers may vary.
Question 8.
The sum of two positive integers is always positive but a (positive integer) – (positive integer) can be positive or negative. What about
(a) (positive) – (negative)
(b) (positive) + (negative)
(c) (negative) + (negative)
(d) (negative) – (negative)
(e) (negative) – (positive)
(f) (negative) + (positive)
Solution:
(a) (positive) – (negative) is always positive.
(b) (positive) + (negative) can be positive ornegative.
(c) (negative) + (negative) is always negative.
(d) (negative) – (negative) can be positive or negative.
(e) (negative) – (positive) is always negative.
(f) (negative) + (positive) can be negative or positive.
Question 9.
This string has a total of 100 tokens arranged in a particular pattern. What is the value of the string?

Solution:
Let’s analyze the sequence of the string:
3, -2, 3, -2, 3, -2

Let’s take a set of 5 tokens as it is repeating, total is 3 – 2 = 1
There are 100 tokens in the string.
Hence total sets = \(\frac{100}{5}\) = 20 sets
Total of 1 set = 1
Hence, the value of the string = 1 × 20 = 20.
![]()
10.5 A Pinch of History Figure it Out (Page No. 268)
Question 1.
Can you explain each of Brahmagupta’s rules in terms of Bela’s Building of Fun, or terms of a number line?
Solution:
We can do it on a number line as follows:
Rules for Addition:
1. 2 + 3 = 5

2. (-2) + (-3) = (-5)

3. -5 + 3 = -2

4. 2 + (-2) = 0

5. (-2) + 0 = -2

Rules for Subtraction:
1. 3 – 2 = 1

2. 2 – 3 = -1

3. 2 – (-3) = 2 + 3 = 5

4. 3 – 3 = 0

5. -3 – 0 = -3

Question 2.
Give your own examples of each rule.
Solution:
Rule 1 If a smaller positive number is subtracted from a larger positive number, then the result is positive.
- Building of Fun If you are on Floor 3 and go down 2 floors, you end up on Floor 1 (which is above the ground) positive.
- Number Line If you are at Floor + 3 on the number line and move left 2 units, you reach +1, which is positive.
Rule 2 If a larger positive number is subtracted from a smaller positive number, the result is negative.
- Building of Fun If you are on the floor 3 and go down 5 floors, you end up on Floor (- 2), which is negative.
- Number Line If you are at + 3 on the number line and move left 5 units, you end up at – 2, which is negative.
- Similarly,’other rules can be explained in terms of Bela’s Building of fun or a number line.