Class 6 Maths Chapter 10 The Other Side of Zero Notes
Integers
Natural Numbers:
Natural numbers are counting numbers i.e. 1, 2, 3,…
Whole Numbers:
If we include 0 (zero) with natural numbers, then they are called whole numbers.
Negative Numbers:
The numbers which are less than 0 are called negative numbers. To differentiate these negative numbers from whole numbers, we use a (-) minus sign attached to the number. This indicates that numbers with negative signs are less than zero.
e.g. 1 less than zero is written as -1, 2 less than zero is written as -2, etc.
Sign with Numbers
In our day-to-day life, we see some situations in which some numbers carry a negative sign and some carry a positive sign. These situations are represented by appropriate signs i.e.’+’ sign and ‘-‘ sign.
e.g. Profit is represented by ‘+’ sign and loss is represented by ‘-‘ sign.
![]()
Integers
If we put the whole numbers and the negative numbers together, then the new collection of numbers will look like …, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, … and this collection of numbers is known as integers. Here, 1, 2, 3,… are said to be positive integers and -1, -2, -3,… are said to be negative integers. Zero is an integer that is neither positive nor negative. One more than a given number gives its successor and one less than that of a given number gives its predecessor.
Example 1.
Write the opposite of each of the following.
(i) Profit of ₹ 50.
(ii) Deposit of ₹ 1000.
(iii) 50 km towards South.
Solution:
The opposite of each is
(i) a loss of ₹ 50.
(ii) withdraw of ₹ 1000.
(iii) 50 km towards North.
Example 2.
Write the following numbers with appropriate signs.
(i) 200 m below sea level.
(ii) 20°C below 0°C temperature.
(iii) 25°C above 0°C temperature.
(iv) A deposit of ₹ 50.
(v) Any four numbers less than 0.
Solution:
(i) 200 m below sea level means -200 m.
(ii) 20°C below 0°C temperature means -20° C.
(iii) 25°C above 0°C temperature means +25°C.
(iv) A deposit of ₹ 50 means ₹ +50.
(v) Every negative integer is less than zero and every positive integer is greater than zero.
∴ Numbers less than zero are -1, -2, -3 and -4.
Example 3.
Write the opposite of each of the following.
(i) Increase in height
(ii) 50 km East
(iii) 200 m below sea level
(iv) Profit of ₹ 1000
(v) Deposit of ₹ 2000
Answer:
(i) Decrease in height
(ii) 50 km West
(iii) 200 m above sea level
(iv) Loss of ₹ 1000
(v) Withdraw of ₹ 2000
Example 4.
Using the ‘+’ or ‘-‘ sign indicates the following.
(i) A train late by 30 min.
(ii) A gain of ₹ 15000.
(iii) 2 km above the Earth’s surface.
(iv) 15°C below the freezing point.
(v) 1 km below the sea level.
Answer:
(i) -30 min
(ii) + ₹15000
(iii) +2 km
(iv) -15°C
(v) -1 km
Addition of Integers
To add two positive integers, we simply add them and to add two negative integers, we first add them and then put a negative sign before the sum.
e.g. (+3) + (+2) = +5 and (-2) + (-3) = -(2 + 3) = -5
![]()
When we have one positive and one negative integer, then we subtract a smaller integer from a higher integer and the answer will take the sign of the integer which has the greater value.
e.g. (-3) + (+2) = -3 + 2 = -1
The sum of two positive integers is always a positive integer and the sum of two negative integers is always a negative integer.
Token Concept for Operation on Integers
Addition can be visualized using tokens to represent positive and negative numbers. Consider a scenario, where you are in a tall building with a lift operated by an attendant. The attendant uses tokens to keep track of how many floors he has moved up or down. Green tokens represent positive numbers (upward movement), while red tokens represent negative numbers (downward movement).
Practical Example
Suppose the attendant starts at the ground floor (floor 0) with an empty pocket. Over time, he collects 5 green tokens and 3 red tokens. To determine his current floor, we can add the numbers the tokens represent.
- Green Tokens +5 (up 5 floors)
- Red Tokens -3 (down 3 floors)
- By calculating the sum (+5) + (-3) = +2, we find that the attendant is on floor 2.
Zero Pair Concept
Each green token (+1) can be paired with a red token (-1) to form a ‘zero pair,’ which cancels out any change in floor level. In the example above, the 5 green tokens and 3 red tokens can be grouped into 3 zero pairs, leaving 2 green tokens. Thus, the attendant is 2 floors above the ground level.
Example 1.
Add +4 and -2 using tokens.
Solution:
Start with 4 green tokens and 2 red tokens.
Form 2 zero pairs.
Result (+4) + (-2) = +2 (2 green tokens remaining).
Example 2.
Add +3 and -5 using tokens.
Solution:
Start with 3 green tokens and 5 red tokens.
Form 3 zero pairs.
Result (+3) + (-5) = -2 (2 red tokens remaining).
Brahmagupta’s Rules for Addition
The sum of two positives is positive.
e.g. 2 + 3 = 5.
The sum of two negatives is negative.
e.g.(-2) + (-3) = -5.
To add a positive number and a negative number, subtract the smaller number (ignoring the sign) from the greater number (ignoring the sign). The sign of the greater number is retained.
e.g. (i) (+6) + (-8) = -2
(ii) 2 + (-3) = -1
(iii) -3 + 5 = 2
The sum of a number and its inverse is zero.
e.g. 2 + (-2) = 0
The sum of any number and zero is the same number.
e.g. -2 + 0 = -2
Example 1.
Write the answer of the following.
(i) (+11) + (+6)
(ii) (+17) + (+37)
(iii) (-23) + (-7)
(iv) (-9) + (-16)
Solution:
(i) (+11) + (+6) = +(11 + 6) = 17
(ii) (+17) + (+37) = +(17 + 37) = 54
(iii) (-23) + (-7) = -(23 + 7) = -30
(iv) (-9) + (-16) = -(9 + 16) = -25
Example 2.
Find the answer of the following.
(i) (-8) + (+9)
(ii) (-11) + (+16)
(iii) (+11) + (-17)
(iv) (+23) + (-6)
Solution:
(i) (-8) + (+9) = (-8) + (+8) + (+1) [∵ 8 + 1 = 9]
= 0 + (+1) [∵ (-8) + (+8) = 0]
= +1
(ii) (-11) + (+16) = (-11) + (+11) + (+5) [∵ 11 + 5 = 16]
= 0 + (+5) [∵ (-11) + (+11) = 0]
= +5
(iii) (+11) + (-17) = (+11) + (-11 – 6) [∵ -17 = -11 – 6]
= (+11) + (-11) + (-6)
= 0 + (-6) [∵ (+11) + (-11) = 0]
= -6
(iv) (+23) + (-6) = (+17) + (+6) + (-6) [∵ 23 = 17 + 6]
= (+17) + 0 [∵ (+6) + (-6) = 0]
= +17
![]()
Example 3.
Find the sum of
(i) 257 and -107
(ii) -18 and 18
(iii) -214, 65 and 104
(iv) -40, -180 and 250
Solution:
(i) We have,
257 + (-107) = (+150) + (+107) + (-107) [∵ 257 = 150 + 107]
= (+150) + 0
= 150 [∵ (+107) + (-107) = 0]
(ii) We have, -18 + (+18) = 0
(iii) We have, -214 + 65 + 104 = -214 + 169
= (-169) + (-45) + 169 [∵ 214 = 169 + 45 ⇒ -214 = (-169) + (-45)]
= (-169) + 169 + (-45)
= 0 + (-45)
= -45 [∵ (-169) + 169 = 0]
(iv) We have, (-40) + (-180) + 250 = -(40 + 180) + 250
= (-220) + 250
= (-220) + (+220) + (+30) [∵ 250 = 220 + 30]
= 0 + 30
= 30 [∵ (-220) + (220) = 0]
Example 4.
Find the sum of
(i) (-8) + (-11) + (6) + (17)
(ii) (36) + (-4) + (-70) + (-8)
(iii) (-26) + (14) + (-1) + (16)
(iv) (-14) + (-16) + (7) + (18)
Solution:
(i) We have, (-8) + (-11) + (6) + (17)
= -(8 + 11) + 6 + 17
= (-19) + 23
= (-19) + (+19) + (+4) [∵ 23 = 19 + 4]
= 0 + (+4)
= 4 [∵ (-19) + (19) = 0]
(ii) We have, (36) + (-4) + (-70) + (-8)
= (36) – (4 + 70 + 8)
= (36) – (82)
= (36) + (-36) + (-46) [∵ 82 = 36 + 46 ⇒ -82 = (-36) + (-46)]
= 0 + (-46)
= -46 [∵ (36) + (-36) = 0]
(iii) We have, (-26) + (14) + (-1) + (16)
= -(26 + 1) + (14) + (16)
= (-27) + (30)
= (-27) +(+27) + (3) [∵ 30 = 27 + 3]
= 0 + 3 [∵ (-27) + (+27) = 0]
= 3
(iv) We have, (-14) + (-16) + (7) + (18)
= -(14 + 16) + (7) + (18)
= (-30) + 25
= (-25) + (-5) + 25 [∵ 30 = 25 + 5 ⇒ -30 = (-25) + (-5)]
= (-25) + (+25) + (-5)
= 0 + (-5) [∵ (-25) + (+25) = 0]
= -5
Addition of Integers with the help of Number Line
Firstly, draw the number line and represent the first integer on it. Then, to add a positive integer number in the first integer, we move right to the first integer and to add a negative integer, we move left to the first integer.
e.g. To add 6 and 2, we start from 6 and go to 2 steps to the right of 6 and reach at 8.
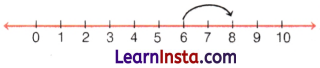
So, 6 + 2 = 8.
Example 5.
Find the solution of the following using a number line.
(i) (-2) + 6
(ii) (-6) + 2
(iii) (-2) + (-9)
(iv) (-3) + 7 + (-5)
Solution:
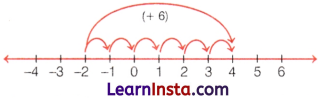
(i) First, mark the integer -2 on the number line. Now, move 6 steps to the right of it. We reach the integer +4.
∴ -2 + 6 = +4
(ii) First, mark the integer -6 on the number line. Now, move 2 steps to the right of it. We reach integer -4.
Hence, -6 + 2 = -4

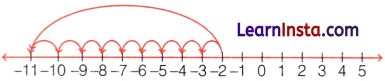
(iii) First, mark the integer -2 on the number line. Now, move 9 steps to the left of it. We reach at integer -11.
∴ (-2) + (-9) = -11
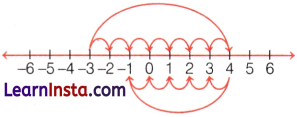
(iv) First, mark the integer -3 on the number line. Now, move 7 steps to the right of the integer. We reach integer +4. Then, move 5 steps to the left of +4. We reach the integer -1.
∴ -3 + (+7) + (-5) = -1
Example 6.
Imagine you are starting on the 4th floor above ground level (floor +4) in a building. If you press the lift button to go down five floors (-5), which floor will you end up on? Write an expression to represent this movement.
Solution:
- Starting floor +4
- Movement -5
- Expression (+4) + (-5) = -1
You will end up on (-1) floor. (1st floor below ground level)
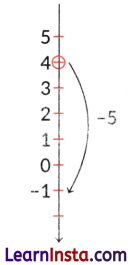
Example 7.
Starting from different floors, find the lift movements needed to reach floor -3.
(i) Starting at floor +2
(ii) Starting at floor 0
Solution:
(i) Starting at floor +2
Movement needed -5.
Expression (+2) + (-5) = -3
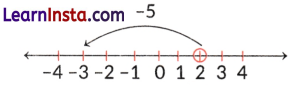
(ii) Starting at floor 0 (ground floor)
Movement needed -3
Expression (0) + (-3) = -3
Example 8.
Find three numbers such that their sum is -10.
Solution:
Let us choose three numbers that add upto -10.
e.g. -3, -4, -3
Verification: -3 + (-4) + (-3) = -10
Example Problems
Question 1.
Write the answer of the following addition.
(i) (+19) + (+3)
(ii) (+41) + (+46)
(iii) (-16) + (-11)
(iv) (-27) + (-16)
(v) (-16) + (+27)
(vi) (+37) + (-11)
(vii) (+9) + (-15)
(viii) (+17) + (-9)
(ix) (+11) + (-14)
(x) (-16) + (+17)
(xi) (-10) + (+31)
(xii) (+13) + (-6)
Answer:
(i) 22
(ii) 87
(iii) -27
(iv) -43
(v) 11
(vi) 26
(vii) -6
(viii) 8
(ix) -3
(x) 1
(xi) 21
(xii) 7
![]()
Question 2.
Find the sum.
(i) 297 and -160
(ii) -46 and 46
(iii) -360, 70 and 180
(iv) -70, -190 and 300
Answer:
(i) 137
(ii) 0
(iii) -110
(iv) 40
Question 3.
Find the sum of the following.
(i) (-11) + (6) + (-13) + (7)
(ii) (17) + (-21) + (-23) + (17)
(iii) (-19) + (31) + (35) + (-16)
(iv) (-41) + (36) + (-41) + (14)
Answer:
(i) -11
(ii) -10
(iii) 31
(iv) -32
Question 4.
Find the solution of the following using a number line.
(i) (-4) + 8
(ii) (-4) + 3
(iii) (-4) + (-6)
(iv) (-4) + (6) + (-8)
Answer:
(i) 4
(ii) -1
(iii) -10
(iv) -6
Question 5.
Using the number line, write the integers which is
(i) 4 more than -2.
(ii) 3 less than -1.
(iii) 6 more than -4.
(iv) 5 less than 4.
Answer:
(i) 2
(ii) -4
(iii) 2
(iv) -1
Question 6.
A man walked 4 km towards North, then he came 7 km towards South. Find his position from the beginning point.
Answer:
3 km towards South
Question 7.
Ravi lives in a building and starts on the 4th floor above ground level (floor +4). He presses the lift button to go down five floors (-5). On which floor will Ravi end up? Write an expression to represent this movement and calculate the final floor.
Answer:
-1
Subtraction of Integers
To subtract an integer from another integer, we add the additive inverse of the integer that is being subtracted from the other integer.
e.g. (-10) – (-4) = (-10) + Additive inverse of -4
= -10 + 4
= -6
i.e. subtraction of an integer is the same as the addition of its additive inverse.
Brahmagupta’s Rules For Subtraction
If a smaller positive is subtracted from a larger positive, the result is positive.
e.g. 3 – 2 = 1
If a larger positive is subtracted from a smaller positive, the result is negative.
e.g. 2 – 3 = -1
Subtracting a negative number is the same as adding the corresponding positive number.
e.g. 2 – (-3) = 2 + 3 = 5
![]()
Subtracting a number from itself gives zero.
e.g. (i) 2 – 2 = 0
(ii) -2 – (-2) = 0
Subtracting zero from a number gives the same number.
e.g. -2 – 0 = -2
Subtracting a number from zero gives the number’s inverse.
e.g. 0 – (-2) = 2
Example 1.
5 – (-3) = 8
Solution:
Subtracting a negative number is the same as adding the corresponding positive number.
Therefore, 5 – (-3) becomes 5 + 3 = 8.
Example 2.
Complete these expressions. Think of them as finding the movement needed to reach the target floor from the starting floor.
(a) (+3) – (+7) = __________
(b) (+2) – (+5) = __________
Solution:
(a) (+3) – (+7) = -4
You need to move 4 floors down to go from the 7th floor to the 3rd floor.
(b) (+2) – (+5) = -3
You need to move 3 floors down to go from the 5th floor to the 2nd floor.
Example 3.
Priya is in a library that has multiple floors. She starts on the 5th floor and wants to reach the 9th floor to find a book. What movement is needed? Write an expression to calculate how many floors Priya needs to move.
Solution:
Starting floor +5
Target floor +9
The movement needed can be calculated using the expression
Movement needed = Target floor – Starting floor
Movement needed = (+9) – (+5) = +4
So, Priya needs to move 4 floors up.
Example 4.
Aman is visiting a friend in an apartment building. He starts on the 2nd floor and needs to reach the basement, which is on the -2nd floor. How many floors does Aman need to move? Write an expression to represent this.
Solution:
Starting floor +2
Target floor -2
The movement needed is
Movement needed = Target floor – Starting floor
Movement needed = (-2) – (+2) = -4
So, Aman needs to move 4 floors down.
Additive Inverse
Numbers such as 4 and -4, 2 and -2 when added to each other give the sum zero. They are called additive inverses of each other.
If two numbers when added to each other give the sum zero, then they are called additive inverse of each other.
e.g. 3 + (-3) = 0.
So, the additive inverse of -3 and -3 is the additive inverse of 3.
Example 5.
Find the value of the following.
(i) -20 – (-5)
(ii) 39 – 16
Solution:
(i) -20 – (-5) = -20 + Additive inverse of -5
We have one negative and one positive value.
So, we will subtract the smaller value from the greater value and take the sign of the greater value = -20 + 5 = -15
(ii) 39 – 16 = 39 + Additive inverse of 16
We have one negative and one positive value.
So, we will subtract the smaller value from the greater value and take the sign of the greater value = 39 + (-16) = 23
Example 6.
Find
(i) (-9) + (-7) – (-80)
(ii) (-14) + 31 – 9 – 1
Solution:
(i) We have, (-9) + (-7) – (-80)
= -(9 + 7) + Additive inverse of -80
= -16 + 80
= 64
(ii) We have, (-14) + 31 – 9 – 1
= (-14) + 31 – 10
= (-14) + 31 + Additive inverse of 10
= (-14) + 31 + (-10)
= -14 – 10 + 31
= -24 + 31
= 7
Example 7.
Subtract the following.
(i) -8 from 13
(ii) -12 from -7
Solution:
(i) 13 – (-8) = 13 + Additive inverse of -8
= 13 + 8
= 21
(ii) -7 – (-12) = -7 + Additive inverse of -12
= -7 + 12
= 5
![]()
Example 8.
Subtract -15 from the sum of 15 and 25.
Solution:
The sum of 15 and 25 = 15 + 25 = 40
Now, subtract -15 from 40.
40 – (-15) = 40 + Additive inverse of -15
= 40 + 15
= 55
Example 9.
The sum of two integers is -33. If one of them is -8. Find the other.
Solution:
Other integer = Sum of two integers – The given integer
= -33 – (-8)
= -33 + Additive inverse of -8
= -33 + 8
= -25
Example 10.
If Ashish is on the ground floor (floor 0) and accidentally presses +5. He wants to stay on the ground floor. What should Ashish do to cancel his movement and stay on the ground floor?
Solution:
To cancel the movement to floor +5, Ashish should press the inverse which is -5.
Expression (+5) + (-5) = 0
By pressing -5, Ashish cancels the effect of pressing +5, bringing him back to the ground floor.
Example 11.
If Abhishek starts on the ground floor and presses +6. After realising, he wants to stay on the ground floor, he presses the inverse. Where will Abhishek end up after pressing +6 and its inverse?
Solution:
First movement +6
Inverse movement -6
Expression (+6) + (-6) = 0
Abhishek ends up back on the ground floor (floor 0).
Example 12.
Fill in the blanks.
(i) (-6) + ______ = 0
(ii) 16 + ______ = 0
(iii) 14 + (-14) = ______
(iv) -4 + ______ = -14
Solution:
(i) We have, (-6) + ______ = 0
⇒ (-6) + 6 = 0 [∵ additive inverse of -6 is 6]
(ii) We have, 16 + ______ = 0
⇒ 16 + (-16) = 0 [∵ additive inverse of-16 is 16]
(iii) We have, 14 + (-14) = ______
⇒ 14 + (-14) = 0 [∵ 14 and -14 are additive inverse of each other]
(iv) We have, (-4) + ______ = -14
Here, the sum of two integers is not zero, so here we cannot write an additive inverse of -4.
⇒ -4+ ______ = -14
⇒ -4 + ______ = -(4 + 10)
⇒ -4 + ______ = (-4) + (-10)
So, on comparing both sides, we get -10 to fill the blank space.
∴ (-4) + (-10) = -14
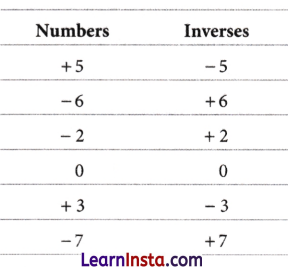
Example 13.
Find the inverses of the following numbers.
+5, -6, -2, 0, +3, -7
Solution:
Subtraction of Integers With the Help of Number Line
Firstly, draw the number line and mark the first integer on it. Then, to subtract a positive integer from the first integer, we move left to the first integer and to subtract a negative integer, we move right to the first integer.
e.g. To subtract 3 from 5, we move 3 steps to the left of 5 and reach at 2.
So, 5 – 3 = 2

and to subtract -4 from 3, we move 4 steps to the right of 3 and reach at 7.

So, 3 – (-4) = 7
![]()
Using the Unmarked Number Line for Addition and Subtraction
An unmarked number line (UNL) is a useful tool for visualizing addition and subtraction (with larger numbers). This line shows only the position of zero while other numbers are implied based on their relative positions.
Example 14.
120 + (-45) = ?
Draw the unmarked number line.

Solution:
Start at 120 on the UNL.
Move 45 units to the left (adding a negative number)
You are now at +75.
Therefore, 120 + (-45) = +75
Example 15.
(-80) – (+130) = ? or 130 + ? = -80
Draw the unmarked number line.

Solution:
Start at -80 on the UNL.
Move 130 units to the left (subtracting a positive number)
You are now at -210.
Thus, (-80) – (+130) = -210
Comparing Using the Number Line
On the number line, the number increases as we move to the right and decreases as we move to the left.
Therefore, -4 < -3 < -2 < -1 < 0 < 1 < 2 < 3 < 4 and so on.
The greater the positive integer, the lesser its opposite.
e.g. 7 > 4 but -7 < -4.
Example 16.
Compare the following pairs of numbers using > or <.
(i) 0 ___ -6
(ii) -1 ___ -12
(iii) 5 ___ -5
(iv) 11 ___ 17
Solution:
(i) We know that -6 is to the left of 0 (zero) on a number line. So, 0 > -6.
(ii) We know -1 is to the right of -12 on the number line. So -1 > -12.
(iii) We know that 5 is to the right of -5. So, 5 > -5.
(iv) We know that 17 is to the right of 11. So, 11 < 17.
Example 17.
Write five negative integers.
(i) greater than -30.
(ii) less than -15.
Solution:
(i) When we move on the number line to the right, then the value of the integer increases.

So, from the above figure, we get the five negative integers greater than -30 are -29, -28, -27, -26, and -25.
(ii) When we move on the number line to the left, then the value of the integer decreases.

So, from the above figure, we get the five negative integers less than -15 are -16, -17, -18, -19, and -20.
Example 18.
Using the concept of floors in a building, compare the following pairs of numbers and fill in the blanks with the correct symbol < or >.
Solution:

Example 19.
In a building, if floor A is -10, floor D is -2 and floor E is +2, then find the floor numbers for B, C, F, G, and H.

Solution:
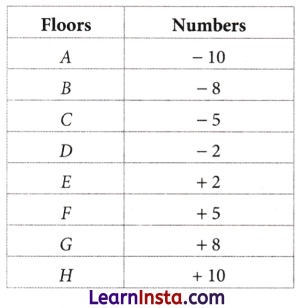
Example 20.
Fill in the blanks with >, < or = sign.
(i) (-5) + (-7) ________ (-5) – (-7)
(ii) (-31) – (-15) ________ (-41) + (-16)
(iii) 30 – (-10) ________ 45 + (-2)
(iv) (-44) – (-21) ________ (-10) – (-35)
Solution:
(i) We have, (-5) + (-7) ________ (-5) – (-7)
LHS = (-5) + (-7) = -12
RHS = (-5) – (-7) = (-5) + Additive inverse of -7 = -5 + 7 = 2
Since, -12 is a negative integer and 2 is a positive integer.
∴ -12 < 2
(ii) We have, (-31) – (-15) ________ (-41) + (-16)
LHS = -31 – (-15) = -31 + Additive inverse of -15
= -31 + 15
= -16
RHS = (-41) + (-16) = -57
Here, both are negative integers but -57 is to the left of -16.
∴ -16 > -57
![]()
(iii) We have, 30 – (-10) ________ 45 + (-2)
LHS = 30 – (-10) = 30 + Additive inverse of -10 = 30 + 10 = 40
RHS = 45 + (-2) = 43
Here, both are positive integers but 43 is right to the 40.
∴ 40 < 43
(iv) We have, (-44) – (-21) ________ (-10) – (-35)
LHS = (-44) – (-21) = -44 + Additive inverse of -21 = -44 + 21 = -23
RHS = (-10) – (-35) = -10 + Additive inverse of -35 = -10 + 35 = 25
Since -23 is a negative integer and 25 is a positive integer.
∴ -23 < 25
Example Problems
Question 1.
Find the value of the following.
(i) 35 – 10
(ii) 70 – 79
(iii) -10 – (-5)
(iv) 10 – (-4)
Answer:
(i) 25
(ii) -9
(iii) -5
(iv) 14
Question 2.
Solve
(i) 8 + (-6) + 4
(ii) (-9) + (-8) – (-7
(iii) 4 – (-3) + (-4) – (3)
(iv) 8 – (-6) + 6 – (-9)
Answer:
(i) 6
(ii) -10
(iii) 0
(iv) 29
Question 3.
Subtract
(i) -6 from 4
(ii) 2 from -10
(iii) 8 from 10
(iv) -11 from -10
Answer:
(i) 10
(ii) -12
(iii) 2
(iv) 1
Question 4.
Subtract -10 from the sum of 10 and 5.
Answer:
25
Question 5.
The sum of two integers is 23. If one of them is -45, then find the other.
Answer:
68
Question 6. Fill in the blanks with >, < or = sign.
(i) (-10) + (-9) _____ (-6) – (-8)
(ii) (-33) – (-14) _____ (-35) + (-14)
(iii) 40 – (-15) _____ 50 + (-7)
(iv) (-22) – (-11) _____ (-15) – (-25)
Answer:
(i) < (ii) >
(iii) >
(iv) <
Question 7.
Fill in the blanks.
(i) (-3) + _____ = 0
(ii) -6 – (-16) = _____
(iii) -8 – _____ = 26
(iv) 19 + (-19) = _____
Answer:
(i) 3
(ii) 10
(iii) -34
(iv) 0
Question 8.
Find the value of the following using a number line.
(i) -9 – (-10)
(ii) 11 – (-2)
(iii) -11 – (-3)
(iv) 11 – 4
Answer:
(i) 1
(ii) 13
(iii) -8
(iv) 7
![]()
Question 9.
Find the additive inverse of the following.
(i) -99
(ii) 11
(iii) -3
(iv) 8
Answer:
(i) 99
(ii) -11
(iii) 3
(iv) -8
Question 10.
Using the concept of floors in a building, compare the following pairs of numbers and fill in the blanks with the correct symbol (< or >).

Answer:
(a) <
(b) <
(c) >
(d) >
(e) >
(f) <
Question 11.
Sneha is on the 3rd floor (floor +3) of her apartment building and accidentally presses the button to go down to the ground floor (floor 0). However, she decides she wants to stay on the 3rd floor. What should Sneha do to cancel her movement and stay on the 3rd floor?
Answer:
(-3)
Question 12.
If floor X = -5, floor Y = -3, and floor Z = +2 in the building shown below as a line, then find the numbers of floors A, B, C, and D.
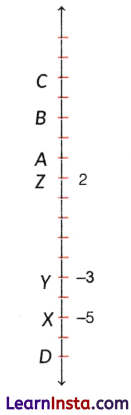
Answer:
3, 5, 7, -7
Application of Integers
Credits and Debits
When you open a bank account, your balance reflects the amount of money you have. Any money deposited into your account is recorded as a ‘credit’ increasing your bank balance. On the other hand, any money withdrawn or spent from your account is recorded as a ‘debit’ which decreases your bank balance. The balance in your bank account is constantly updated based on these credits and debits. Understanding how these transactions affect your balance is crucial for managing your finances.
Example 1.
You start with a bank balance of ₹ 20000. You deposit ₹ 15000 into your account and then withdraw ₹ 8000. What is your new balance?
Solution:
Starting balance = ₹ 20000
Deposit (Credit) = ₹ 15000
Withdrawal (Debit) = ₹ 8000
∴ New balance = Starting balance + Deposit – Withdrawal
New balance = 20000 + 15000 – 8000 = ₹ 27000
Hence, the new balance is ₹ 27000.
Example 2.
Suppose you start with 0 rupees in your bank account and then you have credits of ₹ 20, ₹ 60, and ₹ 70 and debits of ₹ 50, ₹ 30, and ₹ 40. What is your bank account balance now?
Solution:
Total Credits = 20 + 60 + 70 = ₹ 150
Total Debits = 50 + 30 + 40 = ₹ 120
∴ Final balance = Total Credits – Total Debits
Final balance = 150 – 120 = ₹ 30
Geographical Cross-sections
To solve the problem of filling in the respective heights of the geographical features based on the cross-section, you need to understand how to read and interpret the heights about sea level. You can approach this in the following manner.
Given Heights
- Heights above sea level are positive.
- Heights below sea level are negative.
- The sea level is represented as 0 meters.
Example 3.
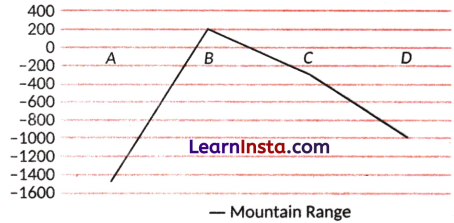
Find the respective heights by looking at the geographical cross-section.
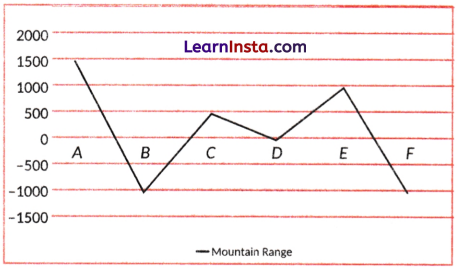
Solution:
A = +1500, B = -1000, C = +500, D = 0, E = +1000 and F = -1000
Understanding Temperature
Celsius (°C) is the unit of measurement for temperature. Temperatures above 0°C indicate warmth, while temperatures below 0°C indicate cold conditions, possibly freezing.
Example 4.
The following are temperature readings from three different places in India during winter.
- Srinagar, Jammu and Kashmir -4°C
- Shimla, Himachal Pradesh 2°C
- Jaipur, Rajasthan 10°C
Arrange these places in order of coldest to warmest.
Solution:
- Coldest Srinagar (-4°C)
- Next coldest Shimla (2°C)
- Warmest Jaipur (10°C)
Example 5.
Imagine you are studying in Vivekananda Kendra Vidyalaya Kipti, Tawang, Arunachal Pradesh. During the winter season, the temperature at 6 PM was 2°C. By 10 PM, the temperature dropped by 5°C. What is the temperature at 10 PM and what does this signify?
Solution:
- Temperature drop = 5°C
- Calculation 2°C – 5°C = -3°C
- Temperature at 10 PM = -3°C
- Significance: The temperature has dropped below freezing, indicating very cold conditions, likely leading to snow.
The Concept of the Border Sum in a 3 × 3 Integer Grid
In a 3 × 3 integer grid, we have three rows and three columns filled with numbers. When we focus on the numbers located on the perimeter (the outer edges of the grid), we can observe something interesting, the sum of the numbers in the top row, bottom row, left column and right column can be made to equal the same value. This value is known as the border sum.
Example 6.
Grid 1
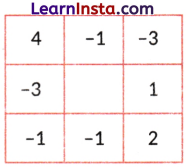
Solution:
Calculating the border sum
Top row = 4 + (-1) + (-3) = 0
Bottom row = -1 + (-1) + 2 = 0
Left column = 4 + (-3) + (-1) = 0
Right column = -3 + 1 + 2 = 0
Border sum = 0
Example 7.
Complete the grid such that the border sum is -3.

Solution:

Example Problems
Question 1.
You start with a bank balance of ₹ 30000. You withdraw ₹ 5000 and then deposit ₹ 12000. What is your new balance?
Answer:
₹ 37000
Question 2.
The following are temperature readings from three different places in India during winter.
(i) Kashmir 2°C
(ii) Dras -5°C
(iii) Leh -8°C
Arrange these places in order from warmest to coolest.
Answer:
Kashmir < Dras < Leh
Question 3.
Imagine you are in Nainital, Uttarakhand. The temperature at 7 AM was 5°C. By noon, the temperature dropped by 10°C. What is the temperature at noon?
Answer:
-5°C
![]()
Question 4.
Construct a 3 × 3 integer grid where the border sum equals -2.
Answer:
Do yourself.
Question 5.
Complete the grid such that the border sum is +5.

Answer:
Do yourself.
Question 6.
Find the heights of the respective places A, B, C and D.
Answer:
A = -1500, B = 200, C = -300 and D = -1000
Class 6 Maths Chapter 10 Notes – Class 6 The Other Side of Zero Notes
→ Counting numbers (natural numbers) are 1, 2, 3, 4, 5,… The smallest natural number is 1 but there is no greatest natural number. If 0 is included in the collection of natural numbers, then the collection is called whole numbers (0, 1,2, 3,4,…).
→ The smallest whole number is 0 and there is no greatest whole number. Every natural number or whole number has a successor. The smallest natural number 1 has no predecessor. Similarly, the smallest whole number 0 also has no predecessor. We can subtract a smaller whole number from a greater whole number.
→ We can also subtract two equal whole numbers from each other. However, the subtraction of a greater whole number from a smaller whole number is not possible.
![]()
→ Negative Numbers
We know that when a whole number is subtracted from an equal whole number, we get 0. If a whole number is subtracted from a smaller whole number, then we get a number that is less than 0. The numbers which are less than zero are called negative numbers.
→ To differentiate these negative numbers from whole numbers, we need to use a sign. The sign that is used is the placement of a minus sign attached to the number. This indicates that numbers with negative signs are less than zero.
For example:
- less than 0 is written as -1,
- less than 0 is written as -2,
- less than 0 is written as -3,
- less than 0 is written as -4, and so on.
→ In general, we use a positive sign (+) with numbers that are above zero and a negative sign (—) with those that are less than zero.
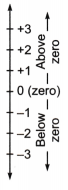
→ Similarly, the steps to the right of zero are represented by the ‘+’ sign, and to the left of zero is represented by the ‘-‘ sign.
→ If the movement of only 1 is made to the right, we get the successor of the number.
→ If the movement of only 1 is made to the left, we get the predecessor of the number.
The predecessor of 0 is -1. The predecessor of -1 is -2.
Predecessor of-2 is -3. Predecessor of -3 is -4 and so on.
Note:
- Every negative number has a predecessor.
- There is no least negative number.
- The greatest negative number is -1.
The successor of -4 is -3. The successor of -3 is -2.
Successor of -2 is -1. Successor of -1 is 0 and so on.
![]()
→ Integers

→ If we take it altogether, then we will get a new collection of numbers, as given below:
…, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5,….
This collection of numbers is known as integers.
The collection of integers has three parts:
→ Let us suppose that the following figures represent the collection of numbers written against them.

→ Then the collection of integers can be understood by the adjoining diagram in which all the earlier collections are included.

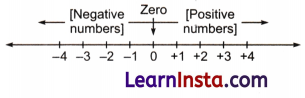
→ On a number line, numbers to the left of zero are called negative numbers.
→ The negative numbers, positive numbers, and zero together form the collection of integers.
→ On a number line, every integer on the right is greater than the integer on the left and vice versa.
→ For adding integers with like signs, we add their numerical values and place the common sign before the sum.
→ For adding integers of unlike signs, we find the difference in their numerical values and give the result the sign of the integer of greater numerical value.
→ If the sum of two integers is 0, they are called the additive inverse of each other.
→ The subtraction of an integer from itself is the same as adding it to its additive inverse.