Students rely on Class 6 Maths Extra Questions Chapter 10 The Other Side of Zero Class 6 Extra Questions and Answers to improve their grades.
Class 6 Maths Chapter 10 Extra Questions The Other Side of Zero
Class 6 Maths The Other Side of Zero Extra Questions
NCERT Class 6 Maths Chapter 10 The Other Side of Zero Extra Questions and Answers
Very Short Answer Type Questions
Question 1.
Write the following numbers with appropriate sign
(i) 100 m below sea level.
(ii) 15°C below 0°C temperature.
Answer:
(i) 100 m below sea level means -100 m.
(ii) 15°C below 0°C temperature means-15°C.
Question 2.
Write the integer which is 2 less than its additive inverse.
Answer:
-1 because 1 – 2 = -1.
Question 3.
Write additive inverse of -121.
Answer:
Additive inverse of-121 is +121.
Question 4.
Find the value of 10 +(-5).
Answer:
Here, 10 + (-5) = 10 – 5 = 5

Question 5.
Write two distinct integers whose sum is equal to one Of the integers. NCERT Exemplar
Answer:
Any two integers with one of them as 0 i.e. 4 and 0.
Question 6.
You start from floor – 5 and press + 7 in the lift. Where will you reach? Write an expression for this movement.
Answer:
Expression Target floor – Starting floor = Movement needed
Starting Floor – 5
Movement Needed + 7
So, the final floor can be calculated as Final floor = -5 + 7 = +2
Question 7.
Evaluate these expressions by thinking of them as the resulting movement of combining button presses:
(-1) + (-4).
Answer:
-5
![]()
Question 8.
Compare the following numbers and fill the box with
< or > -3. – 2.
Answer:
<
Question 9.
Find three numbers such that their sum is -5.
Answer:
-1, 4, -8
Short Answer Type Questions
Question 1.
Represent the following using integers with proper sign
(i) 35 km above sea level.
(ii) A loss Of ₹ 400.
Answer:
Given, statements can be represented using integer
(i) + 35 km
(ii) – ₹ 400
Question 2.
How many integers are there between -8 and -2 ?
Answer:
The integers -7, -6,-5, -4 and -3 lie between -8 and -2. So, there are 5 integers between -8 and -2.
Question 3.
Find the sum of the pairs of integers.
(i) -6,-6
(ii) +4,-3
Answer:
(i) -6, -5 both have negative signs.
So, -6 + (-5) = -(6 + 5) = -11
(ii) +4 and -3 have opposite sign’.
So, 4 + (-3) = 4 – 3 = 1
Question 4.
Find the sum of -3 and -4 using the number line.
Answer:
To add -3 and -4. Mark -3 on the number line. Move 4 steps to left of-3, we reach at -7.
![]()
⇒ -3 + (-4) = – 7
Question 5.
Write two integers whose sum is less than both the integers.
Answer:
For the required integers, we can take any two negative integers.
So, the required integers can be -5, and -7.
Question 6.
Write four pairs of integers which are at the same distance from 2 on the number line. NCERT Exemplar
Answer:
We draw a number line.
![]()
Now, four pairs are (0, 4), (-1,5), (- 3,7) and (1,3).
Question 7.
Write the digits 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9 in this order and insert’+’ or between them to get the result.
(i) 7
(ii) -5
Answer:
(i) To get the sum = 7
0 – 1 + 2 + 3 – 4 + 5 – 6 + 7 – 8 + 9
= 2 + 3 + 5 + 7 + 9 – (1 + 4 + 6 + 8)
= 26 – 19 = 7
(ii) To get the sum = -5
0 – 1 – 2 + 3 + 4 – 5 + 6 +7 – 8 – 9
= 3 + 4 + 6 + 7 – (1 + 2 + 5 + 8 + 9)
= 20 – 25 = – 5
Question 8.
The sum of two integers is 35. If one of the integers is -12, then find the other integer.
Answer:
Given, sum is 35. The other integer is obtained by subtracting -12 from 35.
So, the required integer = 35 – (-12)
= 35 + 12 = 47.
Question 9.
Subtract
(i) 5 from-6
(ii)-3 from-6
Answer:
(i) The additive inverse of 5 is -5.
So,-6 – 5 =-6 + (-5) = -(6 + 5) = -11
(ii) The additive inverse of-3 is +3.
So,-6 – (-3) = -6 + 3 = -3
![]()
Question 10.
Subtract using the number line.
(i) 3 from-2
(ii) -5 from-3
Answer:
(i) Move 3 steps from -2 on the left, we reach at*-5.
![]()
(ii) Move 5 steps front -3 on the right, we reach at 2.
![]()
So,-3 – (-5) = -3 + 5 = 2.
Question 11.
Try to subtract (+ 4) – (- 5). How many zero pairs will you have to put in? What is the result?
Answer:
5 zero pair and result is + 9.
Question 12.
Suppose you start with 0 rupee in your bank account and then you have debits of ₹ 5, ₹ 10, ₹ 20, ₹ 40, ₹ 80, 1 ₹ 160 and ₹ 320 and then a single credit of ₹ 600. What is your bank account balance now?
Answer:
Total Debits: 5 +10 + 20 + 40 + 80 + 160 + 320 = 635
Total Credits: 600
Final Balance Calculation:
Final balance = Total Credits – Total Debits
Final balance = 600 – 635 = – 35
Question 13.
Complete the grid such that the border sum is 0.
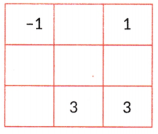
Answer:
Do yourself
Question 14.
From the present year, which year was it 2200 years ago?
Answer:
176 BCE
Long Answer Type Questions
Question 1.
Complete each of the following.
(i) 30 + (-50) + (-20)
(ii) 40 + (-10) + (-15)
(iii) 45 – (-5) + 10
(iv) 60 – 10 + 5 – (-5)
(v) 16 + (-13) + (-10)
(vi) 0 + 5 – (-6) + (-7)
Answer:
According to the rules of addition and subtraction of integers,
(i) 30 + (-50) + (-20) = 30 – (50 + 20)
= 30-70 = -40
(ii) 40 + (-10) + (-15) = 40 – (10 + 15)
= 40 – 25 = 15
(iii) 45 – (-5) + 10 = 45 + 5 + 10 = 60
(iv) 60 – 10 + 5 -(-5) = 60 + 5 + 5 – 10 = 70 – 10 = 60
(v) 16 + (-13) + (-10) = 16 – (13 +10)
= 16 – 23 = -7
(vi) 0 + 5 – (-6) + (-7) =0 + 5 + 6 – 7
= 11 – 7 = 4
Question 2.
If we denote the height of a place above sea level by a positive integer and depth below the sea level by a negative integer, then write the following using integers with the appropriate signs
(i) 200 m above sea level
(ii) 100 m below sea level
(iii) 10 m above sea level
(iv) Sea level
Answer:
(i) 200 m above sea level = + 200 m
(ii) 100 m below sea level = -100 m
(iii) 10 m above sea level = + 10 m
(iv) Sea level = 0
![]()
Question 3.
Write six distinct integers whose sum is 7.
Answer:
Let he six integers be 1,2, -2, 3, -3 and 6.
Now, sum of the above integers
= 1 + 2 + (—2) + 3 + (—3) + 6
We can arrange the numbers, so that the positive integers and the negative integers are grouped together.
We have, 1 + 2 + 3 + 6 + (-2) + (-3) = 12 – 2 – 3
= 12 -5 =7
Hence, the required integers are 1, 2, -2, 3, -3 and 6.
Question 4.
Write the integer which is 4 more than its additive inverse.
Answer:
Firstly, draw a number line.
![]()
Let +1 be an integer and its additive inverse is -1.
From the number line, we see that +1 is 2 more than its additive inverse.
So, we reject this integer.
Again, let +2 be an integer, its additive inverse is -2.
From the number line, we see that +2 is 4 more than its additive inverse.
Hence, the required integer is 2.
Question 5.
Temperature of a place at 12 : 00 noon was + 5°C. Temperature increased by 3°C in first hour and decreased by 1°C in the second hour. What was the temperature at 2 : 00 pm?
Answer:
Given, initial temperature at 12:00 noon was +5°C.
Since, the temperature increased by 3°C in first hour.
∴ Temperature at 1: 00 pm = 5°C+ 3°C = 8°C
Also, the temperature decreased by 1°C in the second hour.
Temperature at 2 : 00 pm = 8°C- 1°C = 7°C
Hence, the temperature at 2 : 00 pm is 7°C.
Question 6.
If Floor A = 3, Floor B = 5 and Floor C = – 1 in the building shown on the right as a line, then find the numbers of floors D, E, F and G.
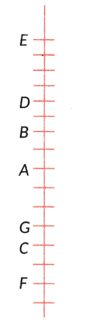
Answer:
D = 7, E = 11, F = -3 G = 0
Question 7.
Complete these expressions. You may think of them as finding the movement needed to reach the target floor from the starting floor.
(a) (+3) – (+6) = ____
Answer:
(+3)-(+6)
Start with + 3 and subtract + 6.
To subtract + 6 from + 3, you need to move 6 units down from + 3 – 6 = – 3
(+3) – (+6) = – 3
(b) (+2)-(+5) = ____
Answer:
(+2) – (+5)
Start with + 2 and subtract + 5.
To subtract + 5 from + 2, you need to move 5 units down from + 2 – 5 = – 3
(+2) – (+5) = – 3
Question 8.
Use unmarked number lines to evaluate these expression
-100 + (- 70) = ____
Answer:

-100 + (-70) = -170
Question 9.
Match the temperature readings with the appropriate time of day/night in Leh, Ladakh, during a day in November.

Answer:
Temperature to Time Matching.
(i) (a) – 6°C
This temperature is extremely cold and is likely to occur in the early hours of the morning. It should be matched with 01:00 am.
(ii) (b) 5°C
This temperature is relatively warmer compared to the other readings and is most likely to be observed during the day. It fits with 03:00 pm.
(iii) (c) – 1°C
This temperature is quite cold but not as extreme, making it suitable for early morning. It should be matched with 07:00 am.
(iv) (d) 0°C
This is a freezing point temperature and would likely be observed late at night. It fits well with 10:00 pm.
Case-Based Questions.
Question 1.
The level of the surface of oceans or seas is called the sea level. Land and hills are raised and are at some height from the sea level.
City A is 10 m below sea level, City B is 28 m below sea level and City C is 14 m above sea level.
(i) Which of the three cities is at the highest elevation from the sea level?
(ii) Aditi uses the following rules to represent the elevation of different locations.
The sea level is considered to be zero elevation. Below sea level is shown using the ‘-’sign.
Above sea level is shown using the ‘+’ sign, e.g. the elevation of City A is shown as -10.
What would be the elevation of City B?
(iii) The elevation of City D is 1 m above the elevation of City B. What is the elevation of City D?
(iv) A submarine at the depth of 45 m rises to 20 m below sea level. What is the depth of the submarine after rising?
(v) A diver at the depth of 60 m spotted a seaweed 23 m below him. What is the depth of the seaweed from the sea level?
(vi) 8-8 = 0
Which of the following is true for the numbers shown above?
(a) -8 is a multiplicative inverse of 8.
(b) – 8 is a multiplicative identity of 8.
(c) -8 is the additive identity of 8.
(d) – 8 is the additive inverse of 8.
Answer:
(i) Let us consider the sea level be 0.
City A is 10 m below sea level is -10.
City B is 28 m below sea level is – 28.
City C is 14 m above sea level is +14.
Hence, City C is at the highest elevation from the sea level.
(ii) – 28 is the elevation for City B.
(iii) City B is 28 m below sea level is – 28.
Add 1 m to the elevation of City B i.e. – 28
-28m + 1 m = – 27m
Hence, – 27 m is the elevation of City D.
(iv) Given, a submarine at the depth of 45 m rises to 20 m below sea level.
Depth of a submarine at 45 m is – 45..
20 m rise below sea level is + 20.
Add the depth rises below sea level – 45 m + (+ 20 m) = – 25 m
Hence, the depth of the submarine after rising is – 25 m.
(v) Given, a diver at the depth of 60 m spotted a seaweed 23 m below him.
⇒ -60 – 23 = -83
Hence, 83 m is the depth of the seaweed from the sea level.
(vi) (d) Given, 8 – 8 = 0
⇒ 8 +(-8) =0
Hence, – 8 is the additive inverse of 8.
![]()
Question 2.
The figure shows the position of the satellite above earth.
PR is the line joining the satellite and the centre of earth. P is the position of the satellite, Q is a point on the surface of earth and R is the centre of earth.
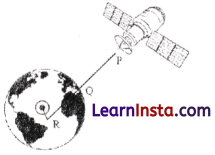
The distance between P and Q is 1300 km and the distance between the centre of earth and the satellite is 7671 km.
(i) What is the distance between the points 0 and R?
(a) 1300 km
(b) 6371 km
(c) 7671 km
(d) 8971 km
Answer:
(b) Distance between Q and R
= Distance between P and R
– Distance between P and Q
⇒ QR = PR- PQ
⇒ QR = 7671 – 1300 = 6371 km
(ii) Shobhit marks Q as zero and the direction from Q to P is positive. What is the distance of R with reference to P?
Answer:
Shobhit marks Q as zero and the direction from Q to P is positive.
Thus, distance from Q to P is + 1300 km.
The distance from P to R is 7671 km.
Q is zero and below Q are negative values.
Hence, – 7671 km is the distance of R with reference to P.
Question 3.
The picture below shows the control panel of a lift in a mall.

0 is the ground floor. The two-wheeler parking area -1 is at basement level 1 and the car parking area -2 is at basement level 2.
(i) Ahmed enters the lift at floor 3 and exits at the two-wheeler parking area. How many floors did the lift go down?
Answer:
Ahmed enters the lift at floor 3 and exists at the two-wheeler parking area -1.
Ahmed travels in lift from
3 → 2, 2 → 1, 1 → 0, 0 → – 1
Hence, the lift goes 4 floors down.
(ii) Meera entered the lift at the car parking floor. She pressed ‘6’ on the control panel of the lift. How many floors up does she want to go?
Answer:
Meera entered the lift at the car parking floor – 2.
She pressed 6 on the control panel of the lift car parking floor is – 2.
Meera starts from – 2.
-2 → -1, -1 → 0, 0 → 1, 1 → 2, 2 → 3, 3 → 4, 4 → 5, 5 → 6
Hence, 8 floors lift goes up.
Class 6 Maths Chapter 10 Extra Questions in Hindi शून्य के दूसरी ओर
The Other Side of Zero Class 6 Extra Questions in Hindi
बहुविकल्पीय प्रश्न
प्रश्न 1.
-3 और -1 के बीच पूर्णांक है-
(a) -3
(b) -1
(c) -2
(d) 0.
उत्तर:
(c) -2
प्रश्न 2.
निम्न में से कौन-सा सत्य है ?
(a) 0 < -8
(b) 0 > -8
(c) 4 < -4
(d) 0 > 6.
उत्तर:
(b) 0 > -8
प्रश्न 3.
निम्न में से कौन-सा असत्य है?
(a) -1 < -2
(b) 79 < 89
(c) -1 < 1
(d) 1 > 0.
उत्तर:
(a) -1 < -2
प्रश्न 4.
निम्न में से कौन-सा कथन सत्य है?
(a) धनात्मक पूर्णांक, ऋणात्मक पूर्णांक से बड़ा होता है।
(b) 0 धनात्मक पूर्णांक से बड़ा होता है।
(c) 0 ऋणात्मक पूर्णांक से छोटा होता है।
(d) इनमें से कोई नहीं
उत्तर:
(a) धनात्मक पूर्णांक, ऋणात्मक पूर्णांक से बड़ा होता है।
प्रश्न 5.
निम्न में से कौन-सा कथन असत्य है?
(a) 0 न तो ऋणात्मक पूर्णांक है और न ही धनात्मक पूर्णांक
(b) 0 धनात्मक पूर्णांक से छोटा होता है।
(c) 0 ऋणात्मक पूर्णांक से बड़ा होता है।
(d) इनमें से कोई नहीं
उत्तर:
(d) इनमें से कोई नहीं
![]()
प्रश्न 6.
निम्न में से कौन-सा कथन सत्य है?
(a) सबसे बड़ा ऋणात्मक पूर्णांक -1 है।
(b) -10 संख्या रेखा पर -8 के दाईं ओर होता है।
(c) -50 संख्या रेखा पर -100 के बाईं ओर होता है।
(d) -11, -10 से बड़ा है।
उत्तर:
(a) सबसे बड़ा ऋणात्मक पूर्णांक -1 है।
प्रश्न 7.
(+1) + (+ 2) = ?
(a) +1
(b) +2
(c) +3
(d) -3.
उत्तर:
(c) +3
प्रश्न 8.
(-1) + (-2) = ?
(a) -1
(b) -2
(c) -3
(d) +3.
उत्तर:
(c) -3
प्रश्न 9.
(-2) + (+3) = ?
(a) -2
(b) +3
(c) +1
(d) -1.
उत्तर:
(c) +1
प्रश्न 10.
(-4) + (+3) = ?
(a) -1
(b) 1
(c ) 0
(d) +2.
उत्तर:
(a) -1