Free access of the complete Ganita Prakash Book Class 6 Solutions and Chapter 9 Symmetry Class 6 NCERT Solutions Question Answer are crafted in simple format to align with the latest CBSE syllabus.
Class 6 Maths Chapter 9 Symmetry Solutions
Symmetry Class 6 Solutions Questions and Answers
9.1 Line of Symmetry Figure it Out (Page 219)
Question 1.
Do you see any Line of symmetry in the figures at the start of the chapter? What about in the picture of the cloud?

Solution:
Flower has 6 lines of symmetry.
Butterfly has 1 line of symmetry.
Rangoli has 4 lines of symmetry.
Pinwheel has no line of symmetry.
A cloud may or may not have a line of symmetry as the shape is not fixed.
Question 2.
For each of the following figures, identify the line(s) of symmetry if it exists.

Solution:

![]()
9.1 Line of Symmetry Figure it Out (Page no. 223 – 230)
Question 1.
In each of the following figures, a hole was punched
In a folded square sheet of paper and then the paper was unfolded. Identify the line along which the paper was folded.
Figure (d) was created by punching a single hole. How was the paper folded?

Solution:

Question 2.
Given the line(s) of symmetry, find the other hole(s):

Solution:

Question 3.
Here are some questions on paper cutting. Consider a vertical fold. How will you vertical fold and a horizontal fold?


Solution:

Question 4.
After each of the following cuts, predict the shape of the hole when the paper is opened. After you have made your prediction, make the cutouts and verify your answer.

Solution:


Solution:


Solution:


Solution:

Question 5.
Suppose you have to get each of these shapes with some folds and a single straight cut. How will you do it?
(a) The hole in the centre is a square.

(b) The hole in the centre is a square.

Solution:

Question 6.
(i) How many lines of symmetry do these shapes have?

(ii) A triangle with equal sides and equal angles.

(iii) A hexagon with equal sides and equal angles.

Solution:
(i) 4 and 8, respectively.
(ii) 3
(iii) 6
Question 7.
Trace each fiure and draw the lines of symmetry, if any:

Solution:


Question 8.
Find the lines of symmetry for the kolam below.

Solution:

Question 9.
Draw the following:
(a) A triangle with exactly one line of symmetry
(b) A triangle with exactly three lines of symmetry
(c) A triangle with no line of symmetry
Is it possible to draw a triangle with exactly two lines of symmetry?
Solution:

No, it is not possible to draw a triangle with exactly two lines of symmetry.
Question 10.
Draw the following. In each case, the figure should contain at least one curved boundary.
(a) A figure with exactly one line of symmetry
(b) A figure with exactly two lines of symmetry
(c) A figure with exactly four lines of symmetry
Solution:

Question 10.
Draw the following. In each case, the figure should contain at least one curved boundary.
(a) A figure with exactly one line of symmetry
Solution:
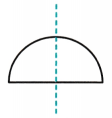
(b) A figure with exactly two lines of symmetry
Solution:
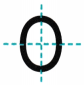
(c) A figure with exactly four lines of symmetry
Solution:
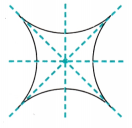
![]()
Question 11.
Copy the following on squared paper. Complete them so that the dotted line is a line of symmetry. Problem (a) has been done for you.


Hint: For (c) and (f), see if rotating the book helps!
Solution:


Question 12.
Copy the following drawing on squared paper. Complete each one of them so that the resulting figure has the two blue lines as lines of symmetry.

Solution:

Question 13.
Copy the following on a dot grid. For each figure draw two more lines to make a shape that has a line of symmetry.

Solution:

![]()
InText Questions
Question 1.
Can you draw a figure with radial arms that has (a) exactly 5 angles of symmetry, (b) 6 angles of symmetry? Also find the angles of symmetry in each case.
Hint: Use 5 radial arms for the first case. What should the angle between two adjacent radial arms be? (Page 235)
Solution:
Yes, we can draw a figure with radial arms that has
(a) exactly 5 angles of symmetry,

The angle between two adjacent radial arms should be 12°.
(b) exactly 6 angles of symmetry,

The angle between two adjacent radial arms should be 60°.
Question 2.
Consider a figure with radial arms having exactly 7 angles of symmetry. What will be its smallest angle of symmetry? Is the number of degrees a whole number in this case? If not, express it as a mixed faction.
Solution:
We cannot draw a figure with radial arms that has exactly 7 angles of symmetry, because the angle between two adjacent radial arms would be 51\(\frac{3}{7}^{\circ}\) which is not a whole number. So, in this case drawing the required figure is very difficult.

9.2 Rotational Symmetry Figure it Out (Page 235 – 236)
Question 1.
Find the angles of symmetry for the given figures about the point marked.

Solution:
(a) 90°
(b) 360°
(c) 180°
Question 2.
Which of the following figures have more than one angle of symmetry?

Solution:
All except (g) have more than one angle of symmetry. rotational symmetry as 360° is its only angle of symmetry.
![]()
Question 3.
Give the order of rotational symmetry for each figure.

Solution:
Order of rotational symmetry to given figure are 2, 4, 6, 3, 4, 5, respectively.
Intext Questions
Question 1.
True or False
Every figure will have 360 degrees as an angle of symmetry. (Pages 236-237)
Solution:
True
Question 2.
If the smallest angle of symmetry of a figure is a natural number in degrees, then it is a factor of 360.
Solution:
True.
9.2 Rotational Symmetry Figure it Out (Page 238)
Question 1.
Color the sectors of the circle below so that the figure has:
(i) 3 angles of symmetry,
(ii) 4 angles of symmetry,
(iii) what are the possible numbers of angles of symmetry you can obtain by coloring the sectors in different ways?

Solution:

(iii) When we rotate this figure by 30°, 60°, 90°, 120°, 150°, 180°, 210°, 240°, 270°, 300°, 330°, and 360°. ‘ We get the original shape. Thus, the possible numbers of angles of symmetry are 12.
Question 2.
Draw two figures other than a circle and a square that have both reflection symmetry and rotational symmetry.
Solution:

![]()
Question 3.
Draw, wherever possible, a rough sketch of the following:
(a) A triangle with at least two lines of symmetry and at least two angles of symmetry
(b) A triangle with only one line of symmetry but not having rotational symmetry
(c) A quadrilateral with rotational symmetry but no reflection symmetry
(d) A quadrilateral with reflection symmetry but not having rotational symmetry
Solution:
(a) Equilateral triangle
Rotational symmetry – equilateral triangle

Suppose it rotates 120°.

The figure looks the same as the previous one.

(b) Isosceles triangle
Line symmetry:

Rotational symmetry:

(c) Parallelogram
A parallelogram is a quadrilateral that has no line of reflection symmetry but has a rotational symmetry of order 2.
Rotational symmetry:

(d) A kite is a quadrilateral with a line of reflection symmetry but not rotational symmetry.

Question 4.
In a figure, 60° is the smallest angle of symmetry. What are the other angles of symmetry of this figure?
Solution:
60°, 120°, 180°, 240°, 300°, 360°
Question 5.
In a figure, 60° is-an angle of symmetry. The figure has two angles of symmetry less than 60°. What is its smallest angle of symmetry?
Solution:
We know that the angles of rotational symmetry are factors of 360°. Since, 60° is an angle of symmetry and two other angles are less than 60°. So, the possible angles of symmetry must be a factor of 60°. These are 30° and 15°. Thus, the smallest angle of symmetry is 15°.
Question 6.
Can we have a figure with rotational symmetry whose smallest angle of symmetry is
(a) 45°
Solution:
Yes, as 360 is divisible by 45.
(b) 17°
Solution:
No, as 360 is not divisible by 17.
Question 7.
This is a picture of the new Parliament Building in Delhi.

(a) Does the outer boundary of the picture have reflction symmetry? If so, draw the lines of symmetries. How many are they?
Solution:
The outer boundary shows rotation symmetry about its center.
Smallest angle of rotation= 360° ÷ 3 = 120°.
Other angles of rotation are 240° and 360°.
(b) Does it have rotational symmetry around its centre? If so, find the angles of rotational symmetry.
Solution:
The outer boundary shows reflection symmetry.

It has 3 lines of symmetry
![]()
Question 8.
How many lines of symmetry do the shapes in the first shape sequence in Chapter 1, Table 3, the regular polygons, have? What number sequence do you get?
Solution:

Similarly, a heptagon has 7 lines of symmetry, an octagon has 8 lines of symmetry, a nonagon has 9 lines of symmetry and a decagon has 10 lines of symmetry. So we can observe that the number of lines of symmetry is equal to the number of sides of the regular polygon.
Question 9.
How many angles of symmetry do the shapes in the first shape sequence in Chapter 1, Table 3, the Regular Polygons, have? What number sequence do you get?
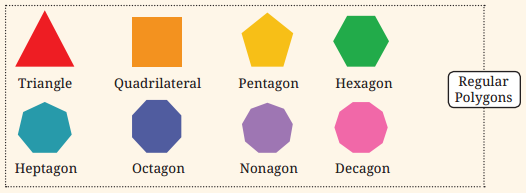
Solution:
- When we rotate triangle (regular polygon) about 120°, 240° and 360°, we get the original shape. Thus, the angles of symmetry are 120°, 240° and 360°. Hence, there are 3 angles of symmetry.
- When we rotate quadrilateral (regular polygon) about 90°, 180°, 270° and 360°. Hence, there are 4 angles of symmetry.
- When we rotate pentagon about 12°, 144°, 216°, 288° and 360°, we get its original shape. Thus, the angle of symmetry are 72°, 144°, 216°, 288° and 360°. Hence, there are 5 angles of symmetry.
- When we rotate hexagon about 60°, 120°, 180°, 240°, 300° and 360°, we get its original shape and these are the angles of symmetry. Thus, there are 6 angles of symmetry.
- Thus, we can say the number of angles of symmetry of regular polygons is same as the number of sides. Therefore, the sequence of angles of symmetry will be 3,4, 5, 6, 7, 8, 9, 10.
Question 10.
How many lines of symmetry do the shapes in the last shape sequence in Chapter 1, Table 3, the Koch Snowflake sequence, have? How many angles of symmetry?

Solution:
Do Yourself
![]()
Question 11.
How many lines of symmetry and angles of symmetry does Ashoka Chakra have?

Solution:
There are 24 lines of symmetry in Ashoka Chakra. Since, the complete rotation is 360°.
Angle of symmetry will be \(\frac{360}{24}^{\circ}\) = 15°.
Thus, when we rotate it about 15°, its original shape is obtained.
And, total number of angles of symmetry is 24.