RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2
Other Exercises
- RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.1
- RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2
- RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere VSAQS
- RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere MCQS
Question 1.
Find the volume of a sphere whose radius is
(i) 2 cm
(ii) 3.5 cm
(iii) 10.5 cm
Solution:
(i) Radius of sphere (r) = 2 cm

Question 2.
Find the volume of a sphere whose diameter is,
(i) 14 cm
(ii) 3.5 dm
(iii) 2.1 m
Solution:
(i) Diameter of a sphere = 14 cm


Question 3.
A hemspherical tank has inner radius of 2.8 m. Find its capacity in litres.
Solution:
Radius of hemispherical tank (r) = 2.8 m

Question 4.
A hemispherical bowl is made of steel 0.25 cm thick. The inside radius of the bowl is 5 cm. Find the volume of steel used in making the bowl.
Solution:
Thickness of steel = 0.25 cm = \(\frac { 1 }{ 4 }\)cm
Inside radius of the hemispherical bowl (r) = 5 cm
∴ Outer radius (R) = 5 + 0.25 = 5.25 cm
∴ Volume of the steel used = \(\frac { 1 }{ 4 }\)π(R3 – r3)

Question 5.
How many bullets can be made out of a cube of lead, whose edge measures 22 cm, each bullet being 2 cm in diameter?
Solution:
Edge of cube (r) = 22 cm
∴ Volume = a3 = (22)3 cm3
= 22 x 22 x 22 = 10648 cm3
Diameter of a bullet = 2 cm

Question 6.
A shopkeeper has one laddoo of radius 5 cm. With the same material how many laddoos of radius 2.5 cm can be made?
Solution:
Radius of bigger laddoo (R) = 5 cm

Question 7.
A spherical ball of lead 3 cm in diameter is melted and recast into three spherical balls. It the diameters of two balls be \(\frac { 3 }{ 2 }\) cm and 2 cm, find the diameter of the third ball.
Solution:
Diameter of a spherical ball of lead = 3 cm

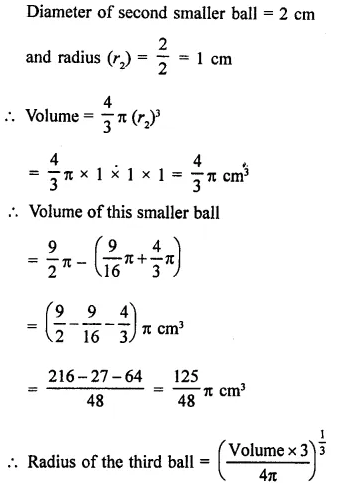

Question 8.
A sphere of radius 5 cm is immersed in water filled in a cylinder, the level of water rises \(\frac { 5 }{ 3 }\) cm. Find the radius of the cylinder.
Solution:
Radius of sphere (r1) = 5 cm
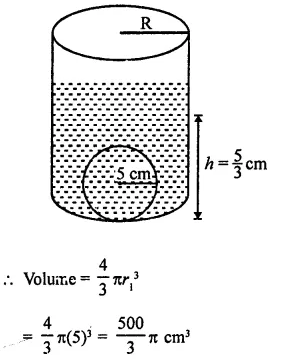
Level of water rises in the cylinder after immersing the sphere in it
∴ Height of water level = \(\frac { 5 }{ 3 }\) cm
Let r be radius of the cylinder, then Volume of water = Volume of the sphere

Question 9.
If the radius of a sphere is doubled, what is the ratio of the volumes of the first sphere to that of the second sphere?
Solution:
Let r2 be the radius of the given sphere
then volume = \(\frac { 4 }{ 3 }\) πr3
By doubling the radius the radius of the new sphere = 2r
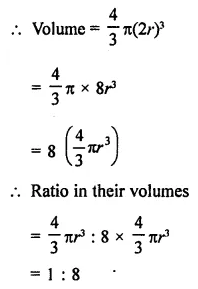
Question 10.
A vessel in the form of a hemispherical bowl is full of water. Its contents are emptied in a right circular cylinder. The internal radii of the bowl and the cylinder are 3.5 cm and 7 cm respectively. Find the height to which the water will rise in the cylinder.
Solution:
Radius of hemispherical bowl (r) = 3.5 cm

Question 11.
A cylinder whose height is two thirds of its diameter, has the same volume as a sphere of radius 4 cm. Calculate the radius of the base of the cylinder.
Solution:
Radius of a sphere (r) = 4 cm

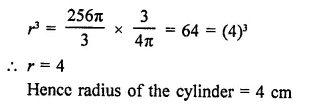
Question 12.
A vessel in the form of a hemispherical bowl is full of water. The contents are emptied into a cylinder. The internal radii of the bowl and cylinder are respectively 6 cm and 4 cm. Find the height of water in the cylinder.
Solution:
Radius of hemispherical bowl (r) = 6 cm

Question 13.
The diameter of a copper sphere is 18 cm. The sphere is melted and is drawn into a long wire of uniform circular cross-section. If the length of the wire is 108 m, find its diameter.
Solution:
Diameter of a copper sphere = 18 cm

Question 14.
The diameter of a sphere is 6 cm. It is melted and drawn into a wire of diameter 0.2 cm. Find the length of the wire.
Solution:
Diameter of a sphere = 6 cm

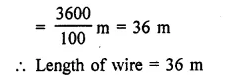
Question 15.
The radius of the internal and external surfaces of a hollow spherical shell are 3 cm and 5 cm respectively. If it is melted and recast into a solid cylinder of height 2 \(\frac { 2 }{ 3 }\) cm. Find the diameter of the cylinder.
Solution:
Internal radius of the hollow spherical shell (r) = 3 cm
and external radius (R) = 5 cm

Question 16.
A hemisphere of lead of radius 7 cm is cast into a right circular cone of height 49 cm. Find the radius of the base.
Solution:
Radius of hemisphere (r) = 7 cm

Question 17.
A hollow sphere of internal and external radius 2 cm and 4 cm respectively is melted into a cone of base radius 4 cm. Find the height and slant height of the cone.
Solution:
Internal radius of a hollow sphere (r) = 2 cm
and external radius (R) = 4 cm
∴ Volume of the metal used

Question 18.
A metallic sphere of radius 10.5 cm is melted and thus recast into small cones each of radius 3.5 cm and height 3 cm. Find how many cones are obtained.
Solution:
Radius of a metallic sphere (R) = 10.5 cm

Question 19.
A cone and a hemisphere have equal bases and equal volumes. Find the ratio Of their heights.
Solution:
Let r be the radius and h be the height of the cone, hemisphere

Question 20.
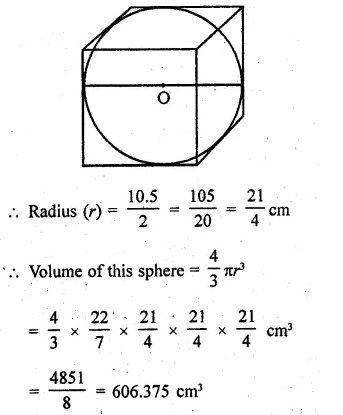
The largest sphere is carved out of a cube of side 10.5 cm. Find the volume of the sphere.
Solution:
By carving a largest sphere out of the cube, the diameter of the sphere = 10.5
Question 21.
A cube, of side 4 cm, contains a sphere touching its sides. Find the volume of the gap in between.
Solution:
Side of cube = 4 cm
∴ Volume = (side)3 = 4x4x4 = 64 cm3
Diameter of the largest sphere touching its sides = 4 cm
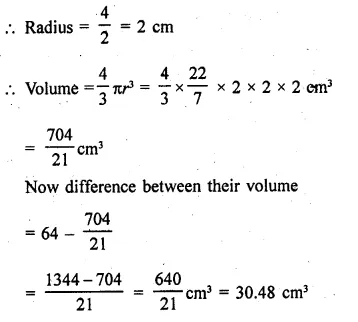
Question 22.
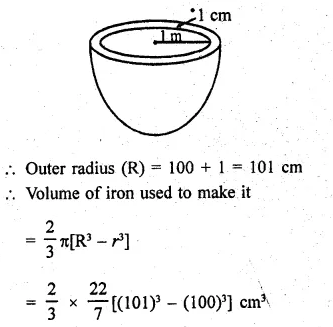
A hemispherical tank is made up of an iron sheet 1 cm thick. If the inner radius is 1m, then find the volume of the iron used to make the tank. (NCERT)
Solution:
Thickness of hemispherical tank = 1 cm
Inner radius (r) = 1 m = 100 cm

Question 23.
A capsule of medicine is in the shape of a sphere of diameter 3.5 mm. How much medicine (in mm3) is needed to fill this capsule? (NCERT)
Solution:
Diameter of a medicine spherical capsule = 3.5 mm
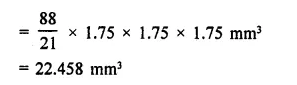
Question 24.
The diameter of the moon is approximately one fourth of the diameter of the earth. What fraction of the volume of the earth is the volume of the moon? (NCERT)
Solution:

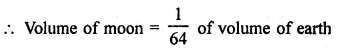
Question 25.
A cone and a hemisphere have equal bases and equal volumes. Find the ratio in their heights.
Solution:
Let r be the radius of cone and hemisphere and let h be the height of the cone then
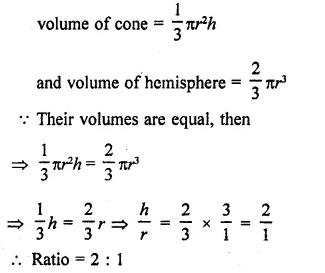
Question 26.
A cylindrical tub of radius 16 cm contains water to a depth of 30 cm. A spherical iron ball is dropped into the tub and thus level of water is raised by 9 cm. What is the radius of the ball?
Solution:
Radius of cylinderical tub (r) = 16 cm
Height of water in it (h) = 30 cm

Question 27.
A cylinder of radius 12 cm contains water to a depth of 20 cm. A spherical iron ball is dropped into the cylinder and thus the level of water is raised by 6.75 cm. Find the radius of the ball. (Use π = 22/7).
Solution:
Radius of cylinder (r) = 12 cm
Depth of water in it (h) = 20 cm
By dropping a ball, the water level rose by 6.75 cm

Question 28.
A cylindrical jar of radius 6 cm contains oil. Iron spheres each of radius 1.5 cm are immersed in the oil. How many spheres are necessary to raise the level of the oil by two centimetres?
Solution:
Radius of cylinderical jar (r) = 6 cm
Level of oil in it (h) = 2 cm
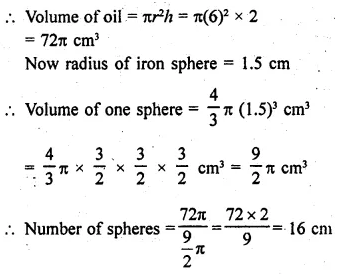
Question 29.
A measuring jar of internal diameter 10 cm is partially filled with water. Four equal spherical balls of diameter 2 cm eacfy are dropped in it and they sink down in water completely. What will be the change in the level of water in the jar?
Solution:
Diameter of measuring jar = 10 cm

Now after swing the ball in the water of jar Let volume of water raised, by h cm
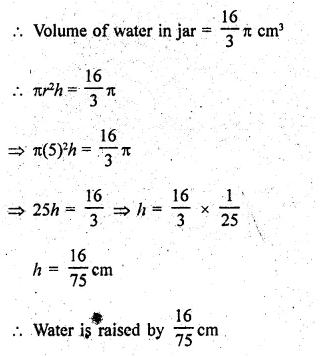
Question 30.
A cone, a hemisphere and a cylinder stand on equal bases and have the same height. Show that their volumes are in the ratio 1 : 2:3.
Solution:
∵ Bases and heights of a cones hemisphere and a cylinder are equal
Let r be the radius and h be their heights
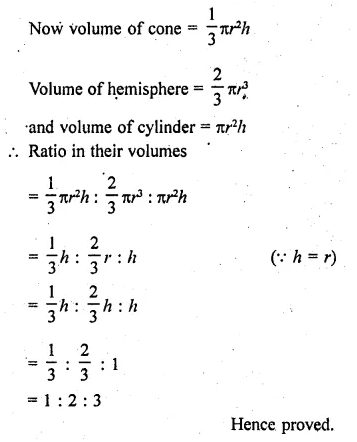
Question 31.
A cylinderical tub of radius 12 cm contains water to a depth of 20 cm. A spherical form ball is dropped into the tub and thus the level of water is raised by 6.75 cm. What is the radius of the ball?
Solution:
Radius of the cylinderical tub (r) = 12 cm
Depth of water in it (h) = 20 cm
By dropping a spherical ball in it, the water raised by 6.75 cm

Question 32.
A sphere, a cylinder and a cone have the same diameter. The height of the cylinder and also the cone are equal to the diameter of the sphere. Find the ratio of their volumes.
Solution:
Diameter of a sphere, cylinder and a cone are equal
Let each as diameter = 2r
Then radius of each = r
Height of cylinder = diameter = 2r
and height of cone = 2r
Now volume of sphere = \(\frac { 4 }{ 3 }\)πr3
Volume of cylinder = πr2h
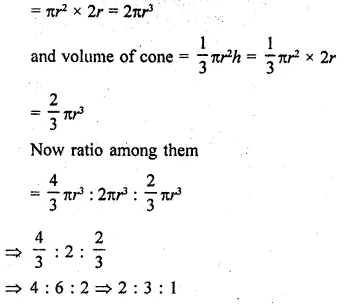
Hope given RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.