RD Sharma Class 10 Solutions Chapter 9 Constructions Ex 9.2
These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 9 Constructions Ex 9.2
Other Exercises
- RD Sharma Class 10 Solutions Chapter 9 Constructions Ex 9.1
- RD Sharma Class 10 Solutions Chapter 9 Constructions Ex 9.2
- RD Sharma Class 10 Solutions Chapter 9 Constructions Ex 9.3
Question 1.
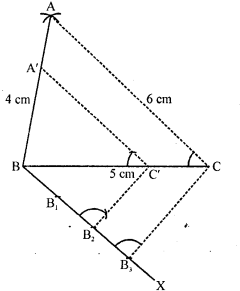
Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are (2/3) of the corresponding sides of it.
Solution:
Steps of construction :
(i) Draw a line segment BC = 5 cm.
(ii) With centre B and radius 4 cm and with centre C and radius 6 cm, draw arcs intersecting each other at A.
(iii) Join AB and AC. Then ABC is the triangle.
(iv) Draw a ray BX making an acute angle with BC and cut off 3 equal parts making BB1 = B1B2= B2B3.
(v) Join B3C.
(vi) Draw B’C’ parallel to B3C and C’A’ parallel to CA then ΔA’BC’ is the required triangle.
Question 2.
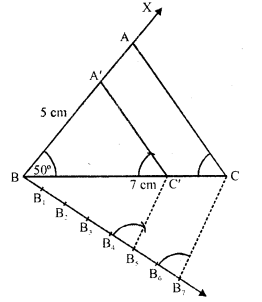
Construct a triangle similar to a given ΔABC such that each of its sides is (5/7)th of the corresponding sides of ΔABC. It is given that AB = 5 cm, BC = 7 cm and ∠ABC = 50°.
Solution:
Steps of construction :
(i) Draw a line segment BC = 7 cm.
(ii) Draw a ray BX making an angle of 50° and cut off BA = 5 cm.
(iii) Join AC. Then ABC is the triangle.
(iv) Draw a ray BY making an acute angle with BC and cut off 7 equal parts making BB, =B1B2=B2B3=B3B4=B4Bs=B5B6=B6B7
(v) Join B7 and C
(vi) Draw B5C’ parallel to B7C and C’A’ parallel to CA.
Then ΔA’BC’ is the required triangle.
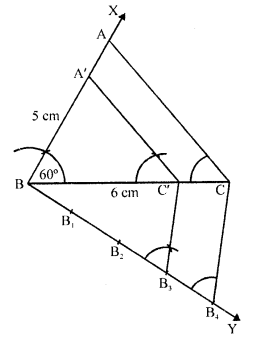
Question 3.
Construct a triangle similar to a given ∠ABC such that each of its sides is \(\frac { 2 }{ 3 }\)rd of the corresponding sides of ΔABC. It is given that BC = 6 cm, ∠B = 50° and ∠C = 60°.
Solution:
Steps of construction :
(i) Draw a line segment BC = 6 cm.
(ii) Draw a ray BX making an angle of 50° and CY making 60° with BC which intersect each other at A. Then ABC is the triangle.
(iii) From B, draw another ray BZ making an acute angle below BC and intersect 3 equal parts making BB1 =B1B2 = B2B2
(iv) Join B3C.
(v) From B2, draw B2C’ parallel to B3C and C’A’ parallel to CA.
Then ΔA’BC’ is the required triangle.

Question 4.
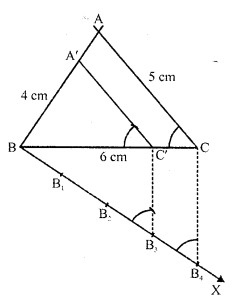
Draw a ΔABC in which BC = 6 cm, AB = 4 cm and AC = 5 cm. Draw a triangle similar to ΔABC with its sides equal to \(\frac { 3 }{ 4 }\)th of the corresponding sides of ΔABC.
Solution:
Steps of construction :
(i) Draw a line segment BC = 6 cm.
(ii) With centre B and radius 4 cm and with centre C and radius 5 cm, draw arcs’intersecting eachother at A.
(iii) Join AB and AC. Then ABC is the triangle,
(iv) Draw a ray BX making an acute angle with BC and cut off 4 equal parts making BB1= B1B2 = B2B3 = B3B4.
(v) Join B4 and C.
(vi) From B3C draw C3C’ parallel to B4C and from C’, draw C’A’ parallel to CA.
Then ΔA’BC’ is the required triangle.
Question 5.
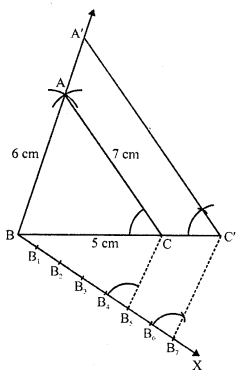
Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle whose sides are \(\frac { 7 }{ 5 }\) of the corresponding sides of the first triangle.
Solution:
Steps of construction :
(i) Draw a line segment BC = 5 cm.
(ii) With centre B and radius 6 cm and with centre C and radius 7 cm, draw arcs intersecting eachother at A.
(iii) Join AB and AC. Then ABC is the triangle.
(iv) Draw a ray BX making an acute angle with BC and cut off 7 equal parts making BB1 = B1B2 = B2B3 = B3B4 = B4B5 = B5B6 = B6B7.
(v) Join B5 and C.
(vi) From B7, draw B7C’ parallel to B5C and C’A’ parallel CA. Then ΔA’BC’ is the required triangle.
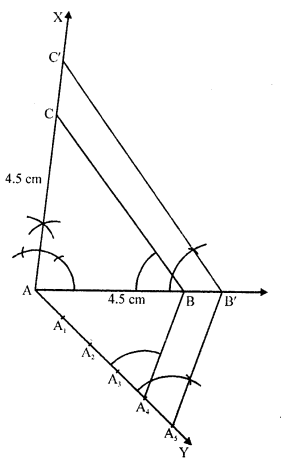
Question 6.
Draw a right triangle ABC in which AC = AB = 4.5 cm and ∠A = 90°. Draw a triangle similar to ΔABC with its sides equal to (\(\frac { 5 }{ 4 }\))th ot the corresponding sides of ΔABC.
Solution:
Steps of construction :
(i) Draw a line segment AB = 4.5 cm.
(ii) At A, draw a ray AX perpendicular to AB and cut off AC = AB = 4.5 cm.
(iii) Join BC. Then ABC is the triangle.
(iv) Draw a ray AY making an acute angle with AB and cut off 5 equal parts making AA1 = A1A2 = A2A3 =A3A4 = A4A5
(v) Join A4 and B.
(vi) From 45, draw 45B’ parallel to A4B and B’C’ parallel to BC.
Then ΔAB’C’ is the required triangle.
Question 7.
Draw a right triangle in which the sides (other than hypotenuse) are of lengths 5 cm and 4 cm. Then construct another triangle whose sides are \(\frac { 5 }{ 3 }\) times the corresponding sides of the given triangle. (C.B.S.E. 2008)
Solution:
Steps of construction :
(i) Draw a line segment BC = 5 cm.
(ii) At B, draw perpendicular BX and cut off BA = 4 cm.
(iii )join Ac , then ABC is the triangle
(iv) Draw a ray BY making an acute angle with BC, and cut off 5 equal parts making BB1 = B1B2 = B2B3 = B3B4 = B4B5
(v) Join B3 and C.
(vi) From B5, draw B5C’ parallel to B3C and C’A’ parallel to CA.
Then ΔA’BC’ is the required triangle.
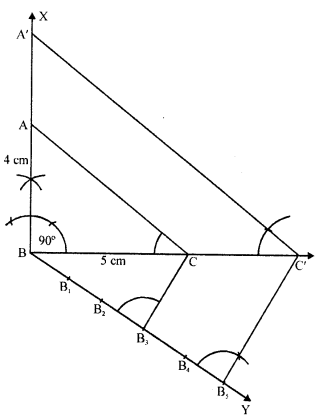
Question 8.
Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose sides are \(\frac { 3 }{ 2 }\) times the corresponding sides of the isosceles triangle.
Solution:
Steps of construction :
(i) Draw a line segment BC = 8 cm and draw its perpendicular bisector DX and cut off DA = 4 cm.
(ii) Join AB and AC. Then ABC is the triangle.
(iii) Draw a ray DY making an acute angle with OA and cut off 3 equal parts making DD1 = D1D2 =D2D3 = D3D4
(iv) Join D2
(v) Draw D3A’ parallel to D2A and A’B’ parallel to AB meeting BC at C’ and B’ respectively.
Then ΔB’A’C’ is the required triangle.
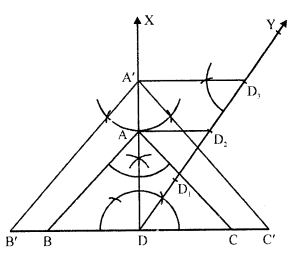
Question 9.
Draw a ΔABC with side BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then construct a trianglewhose sides are \((\frac { 3 }{ 4 } )\)th of the corresponding sides of the ΔABC.
Solution:
Steps of construction :
(i) Draw a line segment BC = 6 cm.
(ii) At B, draw a ray BX making an angle of 60° with BC and cut off BA = 5 cm.
(iii) Join AC. Then ABC is the triangle.
(iv) Draw a ray BY making an acute angle with BC and cut off 4 equal parts making BB1= B1B2 B2B3=B3B4.
(v) Join B4 and C.
(vi) From B3, draw B3C’ parallel to B4C and C’A’ parallel to CA.
Then ΔA’BC’ is the required triangle.
Question 10.
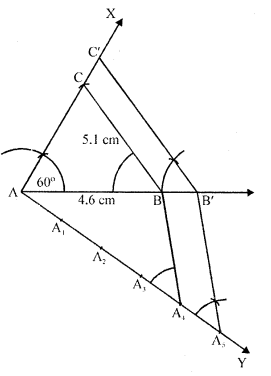
Construct a triangle similar to ΔABC in which AB = 4.6 cm, BC = 5.1 cm,∠A = 60° with scale factor 4 : 5.
Solution:
Steps of construction :
(i) Draw a line segment AB = 4.6 cm.
(ii) At A, draw a ray AX making an angle of 60°.
(iii) With centre B and radius 5.1 cm draw an arc intersecting AX at C.
(iv) Join BC. Then ABC is the triangle.
(v) From A, draw a ray AX making an acute angle with AB and cut off 5 equal parts making AA1 = A1A2 = A2A3 = A3A4=A4A5.
(vi) Join A4 and B.
(vii) From A5, drawA5B’ parallel to A4B and B’C’ parallel to BC.
Then ΔC’AB’ is the required triangle.
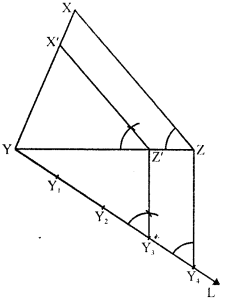
Question 11.
Construct a triangle similar to a given ΔXYZ with its sides equal to \((\frac { 3 }{ 2 })\) th of the corresponding sides of ΔXYZ. Write the steps of construction. [CBSE 1995C]
Solution:
Steps of construction :
(i) Draw a triangle XYZ with some suitable data.
(ii) Draw a ray YL making an acute angle with XZ and cut off 5 equal parts making YY1= Y1Y2 = Y2Y3 = Y3Y4.
(iii) Join Y4 and Z.
(iv) From Y3, draw Y3Z’ parallel to Y4Z and Z’X’ parallel to ZX.
Then ΔX’YZ’ is the required triangle.
Question 12.
Draw a right triangle in which sides (other than the hypotenuse) are of lengths 8 cm and 6 cm. Then construct another triangle whose sides are \(\frac { 3 }{ 4 }\) times the corresponding sides of the first triangle.
Solution:
(i) Draw right ΔABC right angle at B and BC = 8 cm and BA = 6 cm.
(ii) Draw a line BY making an a cut angle with BC and cut off 4 equal parts.
(iii) Join 4C and draw 3C’ || 4C and C’A’ parallel to CA.
The BC’A’ is the required triangle.
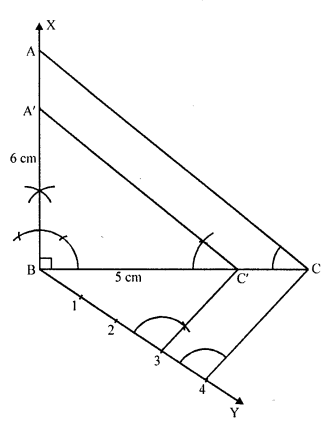
Question 13.
Construct a triangle with sides 5 cm, 5.5 cm and 6.5 cm. Now construct another triangle, whose sides are 3/5 times the corresponding sides of the given triangle. [CBSE 2014]
Solution:
Steps of construction:
(i) Draw a line segment BC = 5.5 cm.
(ii) With centre B and radius 5 cm and with centre C and radius 6.5 cm, draw arcs which intersect each other at A
(iii) Join BA and CA.
ΔABC is the given triangle.
(iv) At B, draw a ray BX making an acute angle and cut off 5 equal parts from BX.
(v) Join C5 and draw 3D || 5C which meets BC at D.
From D, draw DE || CA which meets AB at E.
∴ ΔEBD is the required triangle.
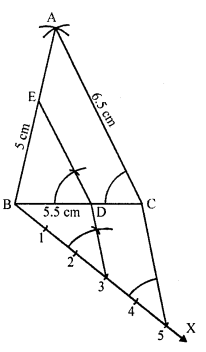
Question 14.
Construct a triangle PQR with side QR = 7 cm, PQ = 6 cm and ∠PQR = 60°. Then construct another triangle whose sides are 3/5 of the corresponding sides of ΔPQR. [CBSE 2014]
Solution:
Steps of construction:
(i) Draw a line segment QR = 7 cm.
(ii) At Q draw a ray QX making an angle of 60° and cut of PQ = 6 cm. Join PR.
(iii) Draw a ray QY making an acute angle and cut off 5 equal parts.
(iv) Join 5, R and through 3, draw 3, S parallel to 5, R which meet QR at S.
(v) Through S, draw ST || RP meeting PQ at T.
∴ ΔQST is the required triangle.
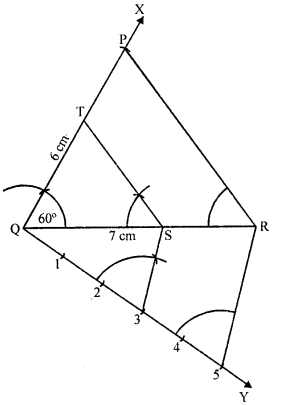
Question 15.
Draw a ΔABC in which base BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then construct another triangle whose sides are \(\frac { 3 }{ 4 }\) of the corresponding sides of ΔABC. [CBSE 2017]
Solution:
Steps of construction:
- Draw a triangle ABC with side BC = 6 cm, AB = 5 cm and ∠ABC = 60°.
- Draw a ray BX, which makes an acute angle ∠CBX below the line BC.
- Locate four points B1, B2, B3and B4 on BX such that BB1 = B1B2=B2B3 = B3B4.
- Join B4C and draw a line through B3 parallel to B4C intersecting BC to C’.
- Draw a line through C’ parallel to the line CA to intersect BA at A’.
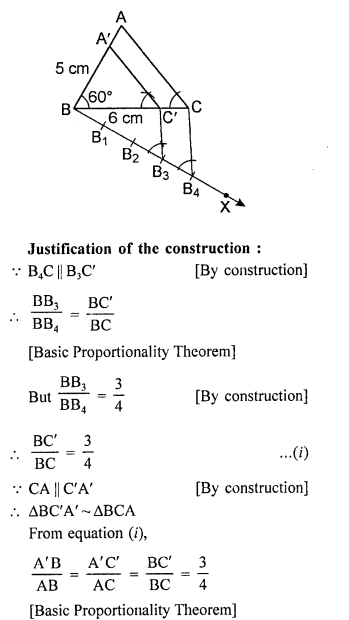
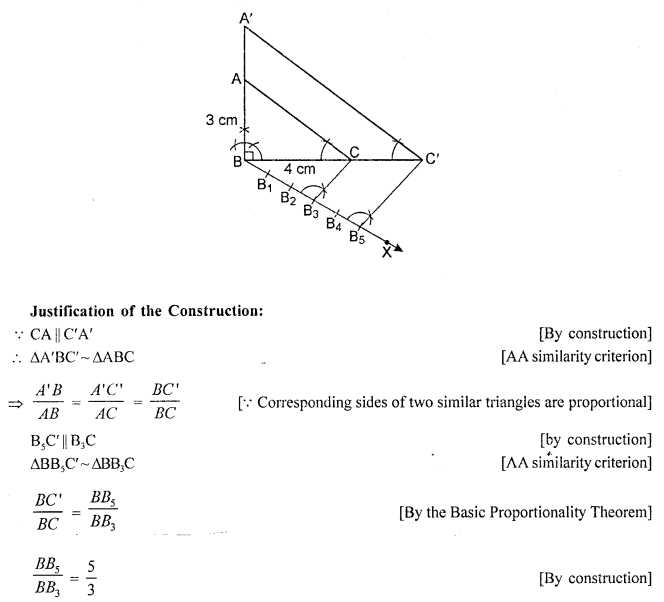
Question 16.
Draw a right triangle in which the sides (other than the hypotenuse) arc of lengths 4 cm and 3 cm. Now, construct another triangle whose sides are \(\frac { 5 }{ 3 }\) times the corresponding sides of the given triangle. [CBSE 2017]
Solution:
Steps of construction:
- Draw a right triangle ABC in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. ∠B = 90°.
- Draw a line BX, which makes an acute angle ∠CBX below the line BC.
- Locate 5 points B1, B2, B3, B4 and B5 on BX such that BB1 = B1B2=B2B3=B3B4=B4B5.
- Join B3 to C and draw a line through B5 parallel to B3C, intersecting the extended line segment BC at C’.
- Draw a line through C’ parallel to CA intersecting the extended line segment BA at A’.
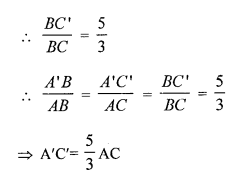
Question 17.
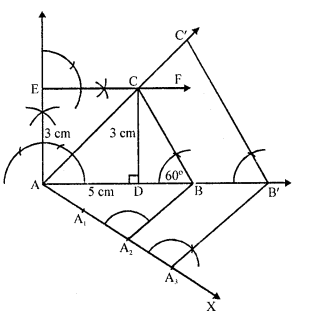
Construct a ΔABC in which AB = 5 cm, ∠B = 60°, altitude CD = 3 cm. Construct a ΔAQR similar to ΔABC such that side of ΔAQR is 1.5 times that of the corresponding sides of ΔACB.
Solution:
Steps of construction :
(i) Draw a line segment AB = 5 cm.
(ii) At A, draw a perpendicular and cut off AE = 3 cm.
(iii) From E, draw EF || AB.
(iv) From B, draw a ray making an angle of 60 meeting EF at C.
(v) Join CA. Then ABC is the triangle.
(vi) From A, draw a ray AX making an acute angle with AB and cut off 3 equal parts making A A1= A1A2 = A2A3.
(vii) Join A2 and B.
(viii) From A , draw A^B’ parallel to A2B and B’C’ parallel toBC.
Then ΔC’AB’ is the required triangle.
Hope given RD Sharma Class 10 Solutions Chapter 9 Constructions Ex 9.2 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.